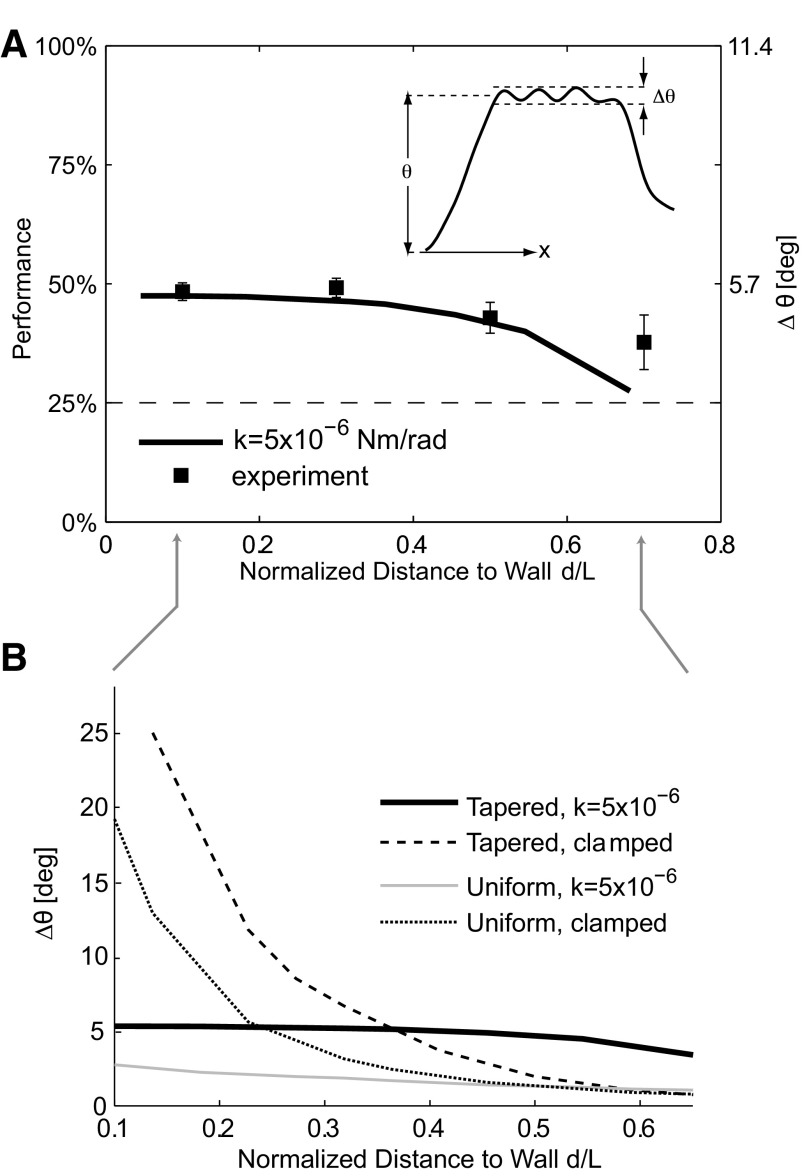
Fig. 6.

Grating discriminability is insensitive to self-motion. A: square symbols, left axis: performance of the classification algorithm as a function of the normalized distance (distance divided by vibrissa length) of the vibrissa base away from the wall. Error bars are SE. The dashed horizontal line represents chance performance (25%). Solid line, right axis: numerically computed (using the finite-element model) amplitude of grating-related variations in the vibrissa angle Δθ (see inset) for grating 2, using the boundary parameters previously inferred (Fig. 4A). In both the experimental data and the model, grating-related information content is relatively invariant for a normalized distance of <0.5, although there is a decrease in grating-related information with distance for a normalized distance >0.5. B: variations in grating-related angle Δθ (for grating 2) as a function of distance as computed by the finite-element model using various boundary conditions and vibrissa geometries (i.e., tapered or uniform cross-section along the vibrissa length). Note that the clamped cases result in a large variation in Δθ, whereas the intermediate case results in a relatively constant Δθ. Furthermore, the tapered geometries result in larger overall responses than the uniform cross-section geometries. The tapered intermediate case, which is the one that most closely matches experimental data, has the largest invariant response over the entire distance range.