Reduced Rank Mixed Effects Models for Spatially Correlated Hierarchical Functional Data

SUMMARY

Hierarchical functional data are widely seen in complex studies where sub-units are nested within units, which in turn are nested within treatment groups. We propose a general framework of functional mixed effects model for such data: within unit and within sub-unit variations are modeled through two separate sets of principal components; the sub-unit level functions are allowed to be correlated. Penalized splines are used to model both the mean functions and the principal components functions, where roughness penalties are used to regularize the spline fit. An EM algorithm is developed to fit the model, while the specific covariance structure of the model is utilized for computational efficiency to avoid storage and inversion of large matrices. Our dimension reduction with principal components provides an effective solution to the difficult tasks of modeling the covariance kernel of a random function and modeling the correlation between functions. The proposed methodology is illustrated using simulations and an empirical data set from a colon carcinogenesis study. Supplemental materials are available online.

1 Introduction

The goal of this paper is to develop a new methodology for modeling hierarchical, spatially correlated functional data, where sub-units are nested within units, which in turn are nested within treatment groups, and the functions are allowed to be correlated at the sub-unit level. There is an extensive literature for modeling independent functional data with various levels of hierarchies; see for example, Shi, et al. (1996), Grambsch et al. (1995), Brumback and Rice (1998), Staniswallis and Lee (1998), Wang (1998), Wang and Wahba (1998), Rice and Wu (2001), Wu and Zhang (2002), Liang, et al. (2003), Morris et al. (2003), and Wu and Liang (2004), Yao et al. (2005a; 2005b), Morris and Carroll (2006), Di et al. (2008), among many others. Recently, Baladandayuthapani, et al. (2008) proposed a Bayesian model for hierarchical, spatially correlated functional data. However, the methodology for dealing with such data is still in its infancy and further development is needed.

In modeling spatially correlated hierarchical functional data we face two major challenges. One is the specification of the covariance structure of random functions. Because of the high dimensionality, it is not feasible for statistical estimation to employ an unstructured covariance specification, which is flexible but requires a large number of unknown parameters. Therefore dimension reduction of some sort is necessary. Some useful covariance specifications with simpler structure have been considered in the literature. For example, diagonal covariance matrices have been used to specify part of the covariance structure by Morris et al. (2003), Morris and Carroll (2006), Baladandayuthapani, et al. (2008). However, such simple structure is often too restrictive in real data analysis. Another challenge is modeling spatial correlation of random functions. This is much less studied in the literature. In the only work we know, Baladandayuthapani, et al. (2008) used a space-time separable covariance structure: while their work is an important step forward, this assumption is hard to justify for real data.

To overcome these challenges, we propose to use functional principal components for both dimension reduction and modeling the spatial correlation of sub-unit level functions. In our functional mixed effects model, an observed functional data object is decomposed as the sum of a fixed treatment effect, a unit level random effect representing unit specific deviation from the treatment effect, a sub-unit level random effect representing sub-unit specific deviation from the unit effect and an error term. The covariance structures of the unit level and sub-unit level random effects are modeled using different sets of principal components and the spatial correlation of sub-unit level random functions is modeled through the spatial correlation of the principal component scores. We use penalized splines to model the mean functions and the principal components functions at both the unit and the sub-unit level. Our approach has two substantial methodological advantages over the existing approach of Baladandayuthapani, et al. (2008): First, a more flexible covariance structure is adapted in our model since principal components instead of pre-specified basis functions are used to represent functional data. Second, we allow a non-separable correlation structure when more than one sub-unit level principal components are used, see Section 2.5 for a detailed discussion. This paper also makes a contribution to modeling hierarchical independent functional data. When no spatial correlation is specified, our modeling framework provides a random effects model alternative to the fixed effects model of Brumback and Rice (1998). In particular, use of two sets of principal components for dimension reduction and modeling covariance structure is new in this context.

The idea of using functional principal components is not new, but most existing work is restricted to independent functions (e.g., Rice and Silverman 1991, Silverman 1996, James et al. 2000, Rice and Wu 2001, Yao, et al. 2005a, 2005b, Di et al. 2009). Recently, Zhou et al. (2008) used principal components to model the correlation of a pair of functions. This paper extends that work in several important aspects. First, the three-level hierarchical data structure presented here is much more complex. Secondly, instead of a pair of correlated functions, a collection of spatially correlated, possibly irregularly positioned functions are considered in this paper. In addition, the complexity of data and model structure introduces substantial computational challenges. Naive extension of Zhou et al. (2008) is theoretically sound but computationally impractical and causes problems with computer storage and computational time. In this paper, we have developed specific techniques to circumvent such difficulties by avoiding storage and computation of large matrices, see the supplemental materials.

Our work is motivated by analyzing data from an experiment using rodent models to investigate the role of p27, an important cell-cycle mediator, in early colon carcinogenesis. To investigate the mechanisms by which diet modulates colon tumor development, rats were fed particular diets of interest for specific periods, exposed to a carcinogen inducing colon cancer and subsequently euthanized for sample collection. The colon was then resected from these rats and colonic cells were examined for response of interest. Colonic cells replicate and grow completely within discrete units called crypts which are finger-like structures that grow into the wall of the colon. The need of a model for spatially correlated hierarchical functional data comes from the following three aspects of the data. First, the data are inherently functional in nature since responses from the cells within each crypt can be viewed as a function of cell position. Second, the experimental data have a three-level hierarchy: crypts are nested within rats, and rats within treatment (diet) groups. In addition, although the rats were independent samples, there may exist spatial correlation at the deepest level of the hierarchy, since within a rat one crypt may behave in accordance with its neighboring crypts.

The rest of the paper is organized as follows. In Section 2, we introduce our model for hierarchical spatially correlated functional data. Section 3 deals with estimation of model parameters and inference. Section 4 discusses some model specification issues including tuning parameter selection for penalized splines and choice of the number of principal components in modeling random functions. Section 5 gives a simulation study that compares our method with that of Baladandayuthapani, et al. (2008). In Section 6 we show the application of our proposed model and method to the colon carcinogenesis data. Section 7 concludes the paper.

2 The Model

Due to the complexity of the data structure, we divide our model specification into four parts: Section 2.1 presents the basic form of our hierarchical mixed effects model of functions; Section 2.2 introduces the dimension reduction for modeling the covariance structure of random functions; Section 2.3 describes how to model the correlation of functions at the sub-unit level of the hierarchy and summarizes the overall covariance structure of the data; Section 2.4 discusses spline models of functions and gives conditions for parameter identifiability. Section 2.5 compares the proposed approach with the Bayesian approach of Baladandayuthapani, et al. (2008).

2.1 Data Structure and Hierarchical Mixed Effects Model

We consider functional data that have a natural hierarchical structure. At the top level of the hierarchy, there are treatment groups; within treatment groups, there are experimental or sampling units and nested within these units are sub-units. For the colon carcinogenesis data we analyze in Section 6, the treatment groups correspond to different diets and time after exposure to the carcinogen, the experimental units are rats and sub-units are colon crypts.

A multilevel model that takes into account the hierarchy is the following:

$$\begin{array}{l}{Y}_{abc}(t)={\mu }_{abc}(t)+{\epsilon }_{abc}(t),\hfill \\ {\mu }_{abc}(t)={\mu }_{ab}(t)+{\eta }_{abc}(t),\hfill \\ {\mu }_{ab}(t)={\mu }_a(t)+{\xi }_{ab}(t),\hfill \end{array}$$ (1)

where t is a generic argument represents the evaluation point of the underlying function, such as cell position on a crypt or time, and Y_abc(t) is the observation of the quantity of interest at t for sub-unit c from unit b of treatment group a. The functions µ_abc(·), µ_ab(·), and µ_a(·) represent true underlying functions of t for an individual sub-unit, unit and treatment level, respectively. We treat µ_a(·) as a fixed effect, modeled as a fixed smooth function; ξ_ab(·) and η_abc(·) are random effects, modeled as realizations from zero mean random processes, and ε_abc(·) are white noise processes. Model (1) can be written succinctly as

$$Y_{abc}(t)={\mu }_a(t)+{\xi }_{ab}(t)+{\eta }_{abc}(t)+{\epsilon }_{abc}(t).$$ (2)

The functions Y_abc(t) are usually observed on a finite number of points t, and the sets of observation points usually vary from sub-unit to sub-unit. The covariance kernels of the random processes ξ_ab(·) and η_abc(·) are bivariate functions, a direct nonparametric fit of which is difficult since ξ_ab(·) and η_abc(·) are latent processes and thus not observable.

2.2 Dimension Reduction with Principal Components

We assume that the important mode of variation of the processes ξ_ab(·) and η_abc(t) can be summarized by a few principal components (PCs). Specifically, for a given treatment group a, we assume the variation of ξ_ab(·) among units within this treatment group is summarized by a set of K_ξ PCs {f_j(·)}. This suggests the reduced rank model

$${\xi }_{ab}(t)={\displaystyle \sum _{j=1}^{K_{\xi }}{f}_j(t){\alpha }_{abj}},$$ (3)

where α_abj are the unit level PC scores, which are assumed to be components of a random vector from a multivariate normal distribution with mean 0 and diagonal covariance matrix D_α,a, f_j(t) are PC functions subject to the orthogonality constraint ∫ f_jf_l dt = δ_jl for j, l = 1, ⋯, K_ξ, δ_jl is the Kronecker delta.

Similarly, for a fixed unit b in treatment group a, we assume the variation of η_abc(·) is summarized by a set of K_η PCs {g_j(·)} and have the model

$${\eta }_{abc}(t)={\displaystyle \sum _{j=1}^{K_{\eta }}{g}_j(t){\beta }_{abcj}},$$ (4)

where β_abcj are the sub-unit level PC scores, which are assumed to be components of a random vector from a multivariate normal distribution with mean 0 and diagonal covariance matrix D_β,a. The PC functions g_j(t) are subject to the orthogonality constraint ∫ g_jg_l dt = δ_jl, j, l = 1, ⋯, K_η.

Use of a few PCs in (3) and (4) effectively reduces the dimensionality of the random effects processes. The difficult task of modeling the covariance kernel of a stochastic process is reduced to modeling the covariance matrix of a low dimensional vector. After dimension reduction with PCs, model (2) becomes

$$\begin{array}{ll}{Y}_{abc}(t)\hfill & ={\mu }_a(t)+{\displaystyle \sum _{j=1}^{K_{\xi }}{f}_j(t){\alpha }_{abj}}+{\displaystyle \sum _{j=1}^{K_{\eta }}{g}_j(t){\beta }_{abcj}}+{\epsilon }_{abc}(t)\hfill \\ \hfill & ={\mu }_a(t)+\mathit{f}{(t)}^{\mathrm{T}}{\mathit{\alpha }}_{ab}+\mathit{g}{(t)}^{\mathrm{T}}{\mathit{\beta }}_{abc}+{\epsilon }_{abc}(t),\hfill \end{array}$$ (5)

where f = (f₁, …, f_Kξ)^T, g = (g₁, …, g_Kη)^T, α_ab = (α_ab1, …, α_abKξ)^T and β_abc = (β_abc1,…,β_abcKη)^T. Here, the mean functions µ_a(·) and the PC functions f₁(·), …, f_Kξ(·), g₁(·), …, g_Kη(·) are fixed but unknown and need to be estimated, the random effects α_ab and β_abc are also unknown and will be treated as missing data when fitting the model. Specification of the joint distribution of the random effects will be given in Section 2.3.

Our formulation and methodology can be extended in a straightforward manner to allow the PC functions to vary among treatment groups. Such extension only involves some notational complication. We will not discuss such extension for simplicity of the presentation.

2.3 Modeling Correlations

With the assumption that all random components in (5) come from normal distributions, we only need to specify the covariance structures to complete the model specification. We assume the unit level random effects are independent and the sub-unit level random effect functions are spatially correlated through the correlation of PC scores. To be specific, we assume that the scores of each PC are realizations of a spatially stationary process. Let x_abc be the physical location of sub-unit c from unit b in treatment group a. It is assumed that for each j, corr (β_abcj, β_abc′j) = ρ(d_cc′; θ_aj), where ρ(·) is a correlation function with a parameter vector θ_aj and d_cc′ = |x_abc − x_abc′| is the Euclidean distance between the sub-units c and c′. Any parametric family of correlation functions can be used for ρ(·, ·) (Stein 1999).

One choice of correlation functions is the Matérn family (Handcock and Stein 1993; Stein 1999), which is used in our numerical examples. The Matérn isotropic autocorrelation function has the general form

$$\rho (d;\varphi ,\nu )=\frac{2^{1-\nu }}{\mathrm{\Gamma }(\nu )}{\left(\frac{2d{\nu }^{1/2}}{\varphi }\right)}^{\nu }{K}_{\nu }(\frac{2d{\nu }^{1/2}}{\varphi }),\varphi >0,\nu >0,$$ (6)

where K_ν(·) is the modified Bessel function of order ν. This Matérn function has two relatively independent parameters. The range parameter, ϕ > 0, controls the rate of decay of the correlation between observations as distance d increases. Large values of ϕ indicate that sites that are relatively far from one another are moderately (positively) correlated. The order parameter ν basically controls the behavior of the autocorrelation function for observations that are separated by small distances.

Our assumptions on the correlation structure can be summarized as follows.

• The unit level PC scores α_abj’s are independent with mean 0 and variance ${\sigma }_{\alpha ,aj}^2$ and the covariance cov(α_abj, α_a′b′j′) = 0 if a ≠ a′ or b ≠ b′ or j ≠ j′. In addition, the α_abj’s are independent of the sub-unit level PC scores β_abcl and the error ε_abc(t);

• The sub-unit level PC scores β_abcj’s are mean 0 and independent with the error ε_abc(t)’s. The covariances are $\text{cov}({\beta }_{abcj},{\beta }_{abc\prime j})={\sigma }_{\beta ,aj}^2\rho (|x_{abc}-x_{abc\prime }|;{\theta }_{aj})$, where ρ(·) is a spatial correlation coefficient depending on the distance between x_abc and x_abc′, and cov(β_abcj, β_{a′b′c′j′}) = 0 if a ≠ a′ or b ≠ b′ or j ≠ j′. Note that the variances of β_abcj’s do not depend on b.

• For the purpose of identifiability, we require that ${\sigma }_{\alpha ,a1}^2>\cdots >{\sigma }_{\alpha ,a{K}_{\xi }}^2$ and ${\sigma }_{\beta ,a1}^2>\cdots >{\sigma }_{\beta ,a{K}_{\eta }}^2$ for a = 1. More details about the identifiability issue will be given in Section 2.4.

• The errors ε_abc(t) are mutually independent with mean 0 and constant variance σ².

To see that our modeling framework allows non-separable correlation structure (Schabenberger and Gotway 2005, Section 9.2), consider two sub-units c and c′ from unit b of treatment group a with physical distance d_cc′. The covariance of the corresponding sub-unit level functions η_abc(t) and η_abc′(t′) is

$$\begin{array}{ll}\text{cov}\{\mathit{g}{(t)}^T{\mathit{\beta }}_{abc},\mathit{g}{(t\prime )}^T{\mathit{\beta }}_{ab{c}^{\prime }}\}\hfill & =\mathit{g}{(t)}^T\text{cov}({\mathit{\beta }}_{abc},{\mathit{\beta }}_{ab{c}^{\prime }})\mathit{g}(t\prime )\hfill \\ \hfill & ={\displaystyle \sum _{j=1}^{K_{\eta }}{\sigma }_{\beta ,aj}^2\rho (d_{cc\prime },{\theta }_{aj})g_j(t)g_j(t\prime ),}\hfill \end{array}$$ (7)

which is in general nonseparable, except when there is only one sub-unit PC (i.e., K_η = 1) or the θ_aj’s do not depend on j. Parsimonious sub-models of our general model can be obtained by removing the dependence of the variances of the random effects on the treatment groups and/or by removing the dependence of the correlation parameters on the treatment groups and the PCs. Such parsimonious sub-models are useful when we do not have enough data to support a flexible specification.

2.4 Modeling Functions with Splines

We choose to fit the mean functions and the PC functions using polynomial splines. Use of polynomial splines can be justified by the good approximation properties of regression splines to smooth functions as well-studied in applied mathematics (de Boor 2001). Other basis expansion approximation of functions can also be used in our methodology. Let b(t) = {b₁(t),⋯, b_q(t)}^T be a spline basis with dimension q. Write µ_a(t) = b(t)^T γ_µ,a, f(t)^T = b(t)^TΓ_ξ and g(t)^T = b(t)^TΓ_η, where γ_µ,a is a q-dimensional vector, a = 1, …, A, Γ_ξ = (γ_ξ,1, …, γ_ξ,Kξ), Γ_η = (γ_η,1, …,γ_η,Kη) are, respectively, a q × K_ξ and a q × K_η matrix of spline coefficients. The reduced rank model (5) then takes the form

$$\begin{array}{l}{Y}_{abc}(t)=\mathit{b}{(t)}^{\mathrm{T}}{\gamma }_{\mu ,a}+\mathit{b}{(t)}^{\mathrm{T}}{\mathbf{\Gamma }}_{\xi }{\mathit{\alpha }}_{ab}+\mathit{b}{(t)}^{\mathrm{T}}{\mathbf{\Gamma }}_{\eta }{\mathit{\beta }}_{abc}+{\epsilon }_{abc}(t),\hfill \\ \hfill a=1,\dots ,A,b=1,\dots ,B_a,c=1,\dots ,C_{ab}.\end{array}$$ (8)

For identifiability, we require that b(t), Γ_ξ and Γ_η satisfy the conditions

$${\displaystyle \int \mathit{b}(t)\mathit{b}{(t)}^{\mathrm{T}}dt=\mathbf{I},}{\mathbf{\Gamma }}_{\xi }^{\mathrm{T}}{\mathbf{\Gamma }}_{\xi }=\mathbf{I},{\mathbf{\Gamma }}_{\eta }^{\mathrm{T}}{\mathbf{\Gamma }}_{\eta }=\mathbf{I}.$$ (9)

The equations in (9) imply orthogonal constraints on the PC functions such that

$${\displaystyle \int \mathit{f}(t)\mathit{f}{(t)}^{\mathrm{T}}dt={\mathbf{\Gamma }}_{\xi }^{\mathrm{T}}{\displaystyle \int \mathit{b}(t)\mathit{b}{(t)}^{\mathrm{T}}dt{\mathbf{\Gamma }}_{\xi }=\mathbf{I},}}$$ (10)

and

$${\displaystyle \int \mathit{g}(t)\mathit{g}{(t)}^{\mathrm{T}}dt={\mathbf{\Gamma }}_{\eta }^{\mathrm{T}}{\displaystyle \int \mathit{b}(t)\mathit{b}{(t)}^{\mathrm{T}}dt{\mathbf{\Gamma }}_{\eta }=\mathbf{I}}.}$$ (11)

See Appendix 1 of Zhou, Huang and Carroll (2008) on how to construct a spline basis b(t) that satisfies the orthonormal constraint given in (9).

Denote ${\mathbf{D}}_{\alpha ,a}=\text{diag}({\sigma }_{\alpha ,a1}^2,\dots ,{\sigma }_{\alpha ,a{K}_{\xi }}^2)$ and ${\mathbf{D}}_{\beta ,a}=\text{diag}({\sigma }_{\beta ,a1}^2,\dots ,{\sigma }_{\beta ,a{K}_{\eta }}^2)$. Only the covariance matrices of Γ_ξα_ab and Γ_ηβ_abc, which are ${\mathbf{\Gamma }}_{\xi }{\mathbf{D}}_{\alpha ,a}{\mathbf{\Gamma }}_{\xi }^{\mathrm{T}}$ and ${\mathbf{\Gamma }}_{\eta }{\mathbf{D}}_{\beta ,a}{\mathbf{\Gamma }}_{\eta }^{\mathrm{T}}$ respectively, can be identified. To identify Γ_ξ, Γ_η, D_α,a, and D_α,a, we need to impose some restrictions on these parameters, as detailed in the following proposition. The result follows directly from the uniqueness of eigen-decomposition of nonnegative definite matrices.

Proposition 1. Assume ${\mathbf{\Gamma }}_{\xi }^{\mathrm{T}}{\mathbf{\Gamma }}_{\xi }=\mathbf{I}$ and ${\mathbf{\Gamma }}_{\eta }^{\mathrm{T}}{\mathbf{\Gamma }}_{\eta }=\mathbf{I}$. In addition, assume that the first nonzero element of each column of Γ_ξ and Γ_η is positive. Suppose the variances of elements of α_1b and β_1bc satisfy ${\sigma }_{\alpha ,11}^2>\cdots >{\sigma }_{\alpha ,1K_{\xi }}^2$ and ${\sigma }_{\beta ,11}^2>\cdots >{\sigma }_{\beta ,1K_{\eta }}^2$. Then the model specified by (8) and (9) is identifiable.

In this proposition, the first nonzero element of each column of Γ_ξ and Γ_η is used to determine the sign at the population level. To minimize the influence by finite sample random fluctuation, in our implementation we have used the elements of the largest magnitude in each column of Γ_ξ and Γ_η to determine the sign. In addition, we suggest to let the first group (a = 1) be the treatment group with the largest sample size to improve stability of the variance estimates.

2.5 Discussion

Baladandayuthapani, et al. (2008) developed a Bayesian approach for modeling the same kind of hierarchical functional data considered by this paper. In their modeling framework, the component functions µ_a(·), µ_ab(·) and µ_abc(·) in (1) and (2) are represented using basis expansions

$${\mu }_a(t)=\mathit{b}{(t)}^{\mathrm{T}}{\gamma }_a,{\mu }_{ab}(t)=\mathit{b}{(t)}^{\mathrm{T}}{\gamma }_{ab},{\mu }_{abc}(t)=\mathit{b}{(t)}^{\mathrm{T}}{\gamma }_{abc},$$

where b(·) is a q-dimensional vector of basis functions, and γ_a, γ_ab, γ_abc are the coefficients in basis expansion. The treatment effects γ_a are assumed to be fixed effects and are given a prior γ_a ~ N(0, Σ₁). The coefficients γ_ab for the unit level functions are mutually independent for different units b and are assumed to have a N(0, Σ_2a) distribution. The coefficients γ_abc for the sub-unit level functions are independent across different units b but may be spatially correlated for different sub-units c within the same sub-unit b. It is assumed that marginally γ_abc ~ N(0, Σ_3a) and, cov(γ_abc, γ_abc′) = ρ(d_cc′; θ_a)Σ_3a where ρ(·; θ_a) is a correlation function with parameter θ_a, d_cc′ is the Euclidean distance between sub-units c and c′. The Matérn family of correlation functions is used in their empirical analysis.

If left unstructured, each of the covariance matrices Σ₁, Σ_2a, and Σ_3a has q(q + l)/2 unique parameters where q equals the number of basis functions used in the basis expansion. Since q can be relatively large, there is an obvious need for dimension reduction. Baladandayuthapani, et al. (2008) proposed the following approach for dimension reduction. They focused on the truncated power basis of quadratic splines

$$\mathit{b}{(t)}^{\mathrm{T}}=(1,m_1(t),m_2(t),{(t-t_1)}_{+}^2,\dots ,{(t-t_k)}_{+}^2),$$ (12)

where (1,m₁(t),m₂(t)) is an orthonormal basis of quadratic polynomials, and t₁, …, t_k are knots of the splines. The covariance matrices of the coefficient vectors are assumed to have a special block diagonal structure, i.e., ${\displaystyle {\sum }_1=\text{diag}(c{\mathit{I}}_3,{\sigma }_1^2{\mathit{I}}_k)}$, ${\displaystyle {\sum }_{2a}=\text{diag}({\displaystyle {\sum }_{2a,}^{*}{\sigma }_2^2{\mathit{I}}_k})}$, ${\displaystyle {\sum }_{3a}=\text{diag}({\displaystyle {\sum }_{3a,}^{*}{\sigma }_3^2{\mathit{I}}_k})}$, where c is a large number serving as a non-informative vague prior, I_k is a k × k identity matrix, ${\displaystyle {\sum }_{2a}^{*}}$ and ${\displaystyle {\sum }_{3a}^{*}}$ are unstructured 3 × 3 matrices. Using the proposed structure reduces the number of parameters to 2 for Σ₁ and to 7 for Σ_2a and Σ_3a.

There are two limitations of the approach by Baladandayuthapani, et al. (2008). First, the covariance structure is assumed separable, that is,

$$\text{cov}\{{\mu }_{abc}(t),{\mu }_{abc\prime }(t\prime )\}=\mathit{b}{(t)}^{\mathrm{T}}\text{cov}({\gamma }_{abc},{\gamma }_{ab{c}^{\prime }})\mathit{b}{(t\prime )}^{\mathrm{T}}=\rho (d_{cc\prime };{\theta }_a)\mathit{b}{(t)}^{\mathrm{T}}{\displaystyle {\sum }_{3a}\mathit{b}}{(\mathit{\text{t′}})}^{\mathrm{T}}.$$ (13)

Separability is a strong assumption that may be hard to justify for a given data set. In comparison, our approach does not impose the separability assumption and thus can provide more reliable inference. Second, the marginal block diagonal covariance structure used by Baladandayuthapani, et al. (2008) is convenient to implement but imposes a usually unrealistic restriction on the data generating process. In contrast, our principal components based dimension reduction can model a broader class of covariance structures. The methodological advantage of our approach is confirmed by simulation results in Section 5.

3 Model Fitting and Inference

3.1 Maximum penalized likelihood

We use the method of penalized maximum likelihood for parameter estimation. Roughness penalties are introduced to regularize the spline fits of functions (Eilers and Marx 1996; Ruppert et al. 2003).

For a = 1, …, A, b = 1, …, B_a, and c = 1, …, C_ab, suppose the observation points of Y_abc(·) are t_abcs, s = 1, …, n_abc. Denote Y_abcs = Y_abc(t_abcs), Y_abc = (Y_abc1, …, Y_abcnabc)^T, and ${\mathit{Y}}_{ab}={({\mathit{Y}}_{ab1}^{\mathrm{T}},\dots ,{\mathit{Y}}_{ab{C}_{ab}}^{\mathrm{T}})}^{\mathrm{T}}$. Recall that b(·) is the q-dimensional spline basis vector. Let b_abcs = b(t_abcs), B_abc = (b_abc1,…,b_abcnabc)^T, ${\mathbf{B}}_{ab}={({\mathbf{B}}_{ab1}^{\mathrm{T}},\dots ,{\mathbf{B}}_{ab{C}_{ab}}^{\mathrm{T}})}^{\mathrm{T}}$, and 𝔹_ab = diag(B_ab1,…,B_abCab). Denote ${\mathit{\beta }}_{ab}={({\mathit{\beta }}_{ab1}^{\mathrm{T}},\dots ,{\mathit{\beta }}_{ab{C}_{ab}}^{\mathrm{T}})}^{\mathrm{T}}$. Denote Γ_η,ab = I_Cab ⊗ Γ_η where I_Cab is the identity matrix of rank C_ab. Model (8) for observed data then can be rewritten as

$${\mathit{Y}}_{ab}={\mathbf{B}}_{ab}{\gamma }_{\mu ,a}+{\mathbf{B}}_{ab}{\mathbf{\Gamma }}_{\xi }{\mathit{\alpha }}_{ab}+{𝔹}_{ab}{\mathbf{\Gamma }}_{\eta ,ab}{\mathit{\beta }}_{ab}+{\mathbf{\epsilon }}_{ab},$$ (14)

where ε_ab = (ε_ab1 (t_ab11),…,ε_ab1(t_ab1nabc),…,ε_abCab(t_abCab1),…,ε_abCab(t_abCabnabCab))^T.

If α_ab and β_ab were observable, the joint likelihood of (Y_ab, α_ab, β_ab) can be factored as

$$L({\mathit{Y}}_{ab},{\mathit{\alpha }}_{ab},{\mathit{\beta }}_{ab})=L({\mathit{Y}}_{ab}|{\mathit{\alpha }}_{ab},{\mathit{\beta }}_{ab})L({\mathit{\alpha }}_{ab})L({\mathit{\beta }}_{ab})$$

because of the independence between α_ab and β_ab. The likelihood of the observed data Y_ab is

$${\displaystyle \int L({\mathit{Y}}_{ab},{\mathit{\alpha }}_{ab},{\mathit{\beta }}_{ab})d{\mathit{\alpha }}_{ab}d{\mathit{\beta }}_{ab}.}$$

We estimate model parameters by minimizing the following penalized likelihood criterion

$$-2{\displaystyle \sum _{a=1}^A{\displaystyle \sum _{b=1}^{B_a}\text{log}\left\{{\displaystyle \int L({\mathit{Y}}_{ab},{\mathit{\alpha }}_{ab},{\mathit{\beta }}_{ab})d{\mathit{\alpha }}_{ab}d{\mathit{\beta }}_{ab}}\right\}}}+{\mathrm{\lambda }}_{\mu }{\mathrm{\Omega }}_{\mu }(\{{\gamma }_{\mu ,a}\})+{\mathrm{\lambda }}_{\xi }{\mathrm{\Omega }}_{\xi }({\mathbf{\Gamma }}_{\xi })+{\mathrm{\lambda }}_{\eta }{\mathrm{\Omega }}_{\eta }({\mathbf{\Gamma }}_{\eta }),$$ (15)

where the Ω’s are roughness penalties and the λ’s are penalty parameters. The roughness penalties will enforce the smoothness of the fitted mean and PC functions.

We define the roughness penalties using the integrated second derivatives of the fitted functions. For the mean functions µ_a(t) = b(t)^Tγ_µ,a, we use the penalty

$${\mathrm{\Omega }}_{\mu }(\{{\gamma }_{\mu ,a}\})={\displaystyle \sum _{a=1}^A{\displaystyle \int {\{{\mu }_a^{″}(t)\}}^2}dt={\displaystyle \sum _{a=1}^A{\gamma }_{\mu ,a}^{\mathrm{T}}}{\displaystyle \int {\mathit{b}}^{″}(t){\mathit{b}}^{″}{(t)}^{\mathrm{T}}dt{\gamma }_{\mu ,a}}}.$$

Similarly, the penalties for the unit and sub-unit level PCs are, respectively,

$${\mathrm{\Omega }}_{\xi }({\mathbf{\Gamma }}_{\xi })={\displaystyle \sum _{j=1}^{K_{\xi }}{\displaystyle \int {\{f_j^{″}(t)\}}^2}dt={\displaystyle \sum _{j=1}^{K_{\xi }}{\gamma }_{\xi ,j}^{\mathrm{T}}{\displaystyle \int {\mathit{b}}^{″}(t){\mathit{b}}^{″}{(t)}^{\mathrm{T}}dt{\gamma }_{\xi ,j}}}}$$

and

$${\mathrm{\Omega }}_{\eta }({\mathbf{\Gamma }}_{\eta })={\displaystyle \sum _{j=1}^{K_{\eta }}{\displaystyle \int {\{g_j^{″}(t)\}}^2}dt={\displaystyle \sum _{j=1}^{K_{\eta }}{\gamma }_{\eta ,j}^{\mathrm{T}}{\displaystyle \int {\mathit{b}}^{″}(t){\mathit{b}}^{″}{(t)}^{\mathrm{T}}dt{\gamma }_{\eta ,j}.}}}$$

Although more flexible specification is possible, we use three penalty parameters, one for all mean functions, one for all unit level PC functions, and one for all sub-unit level PC functions. Selection of these penalty parameters will be discussed in Section 4.1.

Minimization of (15) does not have a closed-form solution. To avoid the computation of the high-dimensional integral in (15), we treat α_ab and β_ab as missing values and use the EM algorithm (Dempster et al. 1977; Laird and Ware 1982) to compute our parameter estimates. At each iteration of the algorithm, given a set of current guesses of the parameter values, the EM algorithm updates the parameter estimates by minimizing the conditional expectation of the −2× log likelihood, where the expectation is taken under the distribution whose parameters are set at their current guesses. Details of the algorithm are given in subsequent subsections. Under mild conditions the EM algorithm converges and each iteration of the EM decreases the negative log likelihood of observed data (Wu, 1983). Our adding roughness penalties to the negative log likelihood does not change the convergence properties of the EM algorithm.

3.2 The EM algorithm

Let $N_{ab}={\displaystyle {\sum }_{c=1}^{C_{ab}}{n}_{abc}}$ and denote V_ab = cov(β_ab). Then −2× joint log likelihood of the “complete data” (Y_ab, α_ab, β_ab) from sub-unit b of unit a is

$$\begin{array}{l}-2l({\mathit{Y}}_{ab},{\mathit{\alpha }}_{ab},{\mathit{\beta }}_{ab};\{{\gamma }_{\mu ,a}\},{\mathbf{\Gamma }}_{\xi },{\mathbf{\Gamma }}_{\eta },{\sigma }^2,\{{\sigma }_{\alpha ,aj}^2\},\{{\sigma }_{\beta ,aj}^2\},{\theta }_{aj})\hfill \\ \begin{array}{ll}\hfill & =N_{ab}\text{log}(2\pi )+N_{ab}\text{log}({\sigma }^2)\hfill \end{array}\hfill \\ \begin{array}{lll}\hfill & \hfill & +{\sigma }^{-2}{({\mathit{Y}}_{ab}-{\mathbf{B}}_{ab}{\gamma }_{\mu ,a}-{\mathbf{B}}_{ab}{\mathbf{\Gamma }}_{\xi }{\mathit{\alpha }}_{ab}-{𝔹}_{ab}{\mathbf{\Gamma }}_{\eta ,ab}{\mathit{\beta }}_{ab})}^{\mathrm{T}}\times \hfill \end{array}\hfill \\ \begin{array}{llll}\hfill & \hfill & \hfill & ({\mathit{Y}}_{ab}-{\mathbf{B}}_{ab}{\gamma }_{\mu ,a}-{\mathbf{B}}_{ab}{\mathbf{\Gamma }}_{\xi }{\mathit{\alpha }}_{ab}-{𝔹}_{ab}{\mathbf{\Gamma }}_{\eta ,ab}{\mathit{\beta }}_{ab})\hfill \end{array}\hfill \\ \begin{array}{lll}\hfill & \hfill & +K_{\xi }\text{log}(2\pi )+\text{log}(|{\mathbf{D}}_{\alpha ,a}|)+{\mathit{\alpha }}_{ab}^{\mathrm{T}}{\mathbf{D}}_{\alpha ,a}^{-1}{\mathit{\alpha }}_{ab}\hfill \end{array}\hfill \\ \begin{array}{lll}\hfill & \hfill & +\{C_{ab}{K}_{\eta }\text{log}(2\pi )+\text{log}(|{\mathbf{V}}_{ab}|)+{\mathit{\beta }}_{ab}^{\mathrm{T}}{\mathbf{V}}_{ab}^{-1}{\mathit{\beta }}_{ab}\}.\hfill \end{array}\hfill \end{array}$$ (16)

The correlation parameters θ_aj enter the likelihood through V_ab. Since sub-units are independent, the −2× joint log likelihood of the “complete data” (Y, α, β) is

$$\begin{array}{l}-2l(\mathit{Y},\mathit{\alpha },\mathit{\beta };\{{\gamma }_{\mu ,a}\},{\mathbf{\Gamma }}_{\xi },{\mathbf{\Gamma }}_{\eta },{\sigma }^2,\{{\sigma }_{\alpha ,aj}^2\},\{{\sigma }_{\beta ,aj}^2\},{\theta }_{aj})\hfill \\ \begin{array}{ll}\hfill & ={\displaystyle \sum _{a=1}^A{\displaystyle \sum _{b=1}^{B_a}\{-2l({\mathit{Y}}_{ab},{\mathit{\alpha }}_{ab},{\mathit{\beta }}_{ab};\left\{{\gamma }_{\mu ,a}\right\},{\mathbf{\Gamma }}_{\xi },{\mathbf{\Gamma }}_{\eta },{\sigma }^2,\left\{{\sigma }_{\alpha ,aj}^2\right\},\left\{{\sigma }_{\beta ,aj}^2\right\},{\theta }_{aj})\}.}}\hfill \end{array}\hfill \end{array}$$ (17)

The E-step of the EM algorithm consists of finding the conditional expectation of (17) given Y_ab and the current parameter values. Since the log likelihood is a quadratic form of the random effects α_ab and β_ab, only their conditional first two moments need to be computed. Details on computing these conditional moments are provided in supplemental materials. Direct calculation of the conditional moments requires the inversion of the matrix cov(Y_ab). This matrix has size N_ab × N_ab with $N_{ab}={\displaystyle {\sum }_{c=1}^{C_{ab}}{n}_{abc}}$, which is often very large. In our empirical example, for a typical rat, there are about C_ab = 20 crypts and n_abc = 30 observations on each crypt, so the matrix to be inverted is of size 600 × 600. By repeatedly applying the Sherman-Morrison-Woodbury formula, we developed the computational devices to circumvent the inversion of this matrix; see Supplemental materials for details.

The M-step of the EM algorithm updates the parameter estimates by minimizing the objective function which is the conditional expectation of −2× log likelihood given in (17), or by reducing the value of this objective function as an application of the generalized EM algorithm. The parameters are well separated in the expression of the conditional log-likelihood, so that we can update the parameter estimates sequentially given their current values. We update according to the following order: (1) σ²; (2) ${\sigma }_{\alpha ,ai}^2$ and ${\sigma }_{\beta ,aj}^2$, a= 1, …, A, i = 1, …, K_ξ and j = 1, …, K_η; (3) γ_µ,a, a = 1, …, A; (4) Γ_ξ; (5) Γ_η; (6) the correlation parameter θ_aj, a = 1, …, A, j = 1, …, K_η. Details of the updating formula are given in supplemental materials. Note that when updating Γ_ξ and Γ_η, some care is needed to enforce the orthonormal constraints.

In our implementation of the EM algorithm, the initial values are obtained using the following procedure. We sequentially fit fixed effects models to obtain raw estimates of the treatment group level, unit level and sub-unit level functions appeared in (2). We first obtain estimates of the treatment effects η_a(t) by fitting fixed effects models with working independent covariance structures and use these raw estimates as the initial values of the treatment effects. Next, we remove the treatment effects from the data and obtain the unit level effects ξ_ab(t) by fitting separate fixed effects models for each unit. Then, removing both the treatment effects and unit level effects we obtain the sub-unit level effects η_abc(t) by fitting separate fixed effects models for each sub-unit. After raw estimates of unit level and sub-unit level functions are obtained, the standard principal components analysis is applied to get the initial estimates of functional principal components and associated variances. When obtaining the unit and sub-unit level effects, the ridge regression with a small ridge parameter is used to deal with the singularity problem caused by small sample size in fixed effects regression. The initial value of the error variance is obtained using the sample variance of the residuals after removing the treatment effects, the unit level and sub-unit level functions from the data. The initial values of the correlation parameters are chosen to be the midpoint of a prespecified interval. With starting values generated by this procedure, the EM algorithm works well in our simulation and real data analysis; it usually converges within twenty steps.

3.3 Prediction of random effects functions and inference

Using estimated parameters, the best linear unbiased predictors (BLUP, Henderson 1950) of the random effects α_ab and β_ab are given by α̂_ab = E(α_ab|Y_ab) and β^_ab = E(β_ab|Y_ab), whose closed-form expressions are available in the supplemental materials. The BLUP of the unit level random function ξ_ab(t) in (2) is f̂(t)^Tα^_ab and the BLUP of the sub-unit level random function η_abc(t) is ĝ(t)^Tβ^_abc, where f̂(t) and ĝ(t) are vectors of estimated unit level and sub-unit level PCs respectively.

The bootstrap (Efron 1979) can be used to obtain standard errors of the parameter estimates. In a nonparametric bootstrap, we resample units without replacement to ensure that the covariance structure in the original sample is preserved in the bootstrap sample. In a parametric bootstrap, we draw bootstrap samples from the model with fitted parameters. After bootstrap samples are drawn, we estimate the model parameters for each bootstrap sample and obtain a collection of resampled estimates. The sample standard deviations of these resampled estimates provide estimates of the desired standard errors. Alternatively, the sample quantiles of the resampled estimates can be used directly to construct bootstrap confidence intervals.

4 Model Selection and Assessment

4.1 Specification of Splines and Penalty Parameters

When using penalized splines to fit smooth functions, degree two or three splines are commonly used, and the placement and number of knots is generally not crucial since the penalty takes care of overfitting (Ruppert 2002). For a typical application, 10–20 knots equally spaced over the data range is often sufficient and fewer knots can be used when the sample size is small or noise level is high.

To choose penalty parameters, one can calculate the crossvalidated score, defined as the crossvalidated −2× log likelihood, and select the parameters corresponding to the minimum. Details on computing the observed data log likelihood without forming the large covariance matrix cov(Y_ab) are given in supplemental materials. To preserve the covariance structure in the data, the data from a whole unit needs to be deleted and serve as a validation set in the crossvalidation. When there are a large number of units, K-fold crossvalidation can be used for computational efficiency. There are three penalty parameters in our method, so we need to search over a three dimensional space for a good choice of these parameters. A multidimensional optimization algorithm can be used to speed up the search. We applied the downhill simplex method of Nelder and Mead (1965) in our implementation of the method.

4.2 Selection of the Number of Significant PCs

To determine the number of important PCs at both the unit level and the sub-unit level, first note that the available data usually set an upper bound on the feasible number of PCs we can fit in the model. If too many PCs are acquired from the EM algorithm, numerical problems may occur such as inversion of singular matrices and the algorithm failing to converge. This is precisely the reason dimension reduction through use of principal components is needed. See James et al. (2000) for a similar discussion in the case of functional data without spatial correlation. Leave-one-unit-out crossvalidation or its K-fold version can be used to decide on the number of significant PCs. This strategy works well in our simulation studies: it can correctly identify the number of PCs in the data generating model most of times, see Section 5.

In actual data analysis, however, the crossvalidation score may keep on decreasing as more PCs are included in the model. This phenomenon, also observed in application of principal components analysis in multivariate analysis, is not surprising since a reduced rank model with a finite number of PCs is typically only an approximation. We can still use crossvalidation, not to identify the “correct” model, but to identify the most parsimonious model that fits the data well. If one arranges the crossvalidation scores according to the increasing complexity of the model, one usually sees a quick drop of the crossvalidation scores, followed by much slower decrease; the turning point suggests the suitable number of PCs. See Section 6 for an illustration of this method.

4.3 Model assessment

Various diagnostic plots can be used to assess whether the number of PCs selected by cross-validation is sufficient and how well the model fits the data. At the unit level, using too few PCs will force some unit level effects to be included into the estimates of the sub-unit level effects. Thus deviation from zero of the unit mean of fitted sub-unit level effects for some units indicates an insufficient number of PCs at the unit level. At the sub-unit level, if too few PCs are fitted, a pattern will appear in the unit-wise residual plots. Thus examination of the unit-wise residual plots can help assess whether the number of PCs obtained from crossvalidation is sufficient at the sub-unit level. The normal quantile-quantile plots of fitted random effects and of residuals can be used to assess the distributional assumptions in the model.

5 Simulation

In this section we illustrate the performance of our method using simulated data and compare it with the Bayesian method of Baladandayuthapani, et al. (2008). The two methods differ mainly in the specification of the covariance structure. When setting up the simulation studies, we considered not only generating data from our reduced rank model but also from the model of Baladandayuthapani, et al. (2008). We used the existing computer code from the original paper when applying the Bayesian method.

The errors of estimating the treatment group means are measured using the following integrated absolute errors

$${\displaystyle \int |{\widehat{\mu }}_a(t)-{\mu }_a(t)|dt},$$

where a denotes the treatment group and the hat indicates estimated values. The errors from all treatment groups are then averaged to get a summary measure. To facilitate comparison of the estimated covariance structure from the two methods, we examined the predictions of the unit level and sub-unit level random effects. These predictions are given by the posterior means of the relevant quantities using the estimated covariance structure. Using the notation in (2) of Section 2.1, the errors of predicting the random effects are measured using the integrated absolute errors

$${\displaystyle \int |{\widehat{\xi }}_{ab}(t)-{\xi }_{ab}(t)|dt}\text{\hspace{1em}and\hspace{1em}}{\displaystyle \int |{\widehat{\eta }}_{abc}(t)-{\eta }_{abc}(t)|dt}$$

for treatment a, unit b, and sub-unit c, where the hats indicate predicted values. All unit level errors are then averaged to get a summary measure at the unit level. Similarly, all sub-unit level errors are averaged to get a summary measure at the sub-unit level. In our calculations, the integrals were approximated using a Riemann sum with a grid of 20 equally spaced points.

In all simulations, there were two treatment groups, twelve units within each treatment group, twenty sub-units within each unit and twenty observations on each sub-unit. For each unit, the twenty sub-units were located on a line segment with locations independently generated from the uniform distribution on [0, 14]. For each sub-unit, the functional response Y(t) was evaluated at twenty points randomly generated from the uniform distribution on [0, 1]. Details of setting up the mean and principal components functions, variance and correlation parameters are given below. We ran the simulation 100 times for each setup and used the measures described above to assess/compare the performance of the two methods. When applying our method to the simulated data, we used cubic splines with five interior knots to fit the functions and used crossvalidation to select the penalty parameters.

We first considered three different setups from our reduced rank model where we fixed the forms of the mean and PC functions but varied other parameters of the model. The mean curves for the two treatment groups were

$${\mu }_1(t)=7-16t+30t^2-15t^3\text{\hspace{1em}and\hspace{1em}}{\mu }_2(t)=8-13t+14t^2-t^3.$$

The unit level PC functions were

$$f_1(t)=1.414\text{sin}(2\pi t)\text{\hspace{1em}and\hspace{1em}}{f}_2(t)=-1.485+2.970\text{sin}(\pi t)$$ (18)

and the sub-unit level PC functions were

$$g_1(t)=1\text{\hspace{1em}and\hspace{1em}}{g}_2(t)=-1.118+3.354t^2.$$ (19)

The five-fold crossvalidation identified the correct number of PCs in more than 95% of the cases, in each setup.

Setup 1. We used a model with one unit level PC f₁(t) given in (18) and one sub-unit level PC g₁(t) given in (19). At the unit level, the PC score variances ${\sigma }_{\alpha ,11}^2=0.64$ for treatment group 1 and ${\sigma }_{\alpha ,21}^2=0.16$ for treatment group 2; at the sub-unit level, the PC score variances ${\sigma }_{\beta ,11}^2=0.36$ for treatment group 1 and ${\sigma }_{\beta ,21}^2=0.16$ for treatment group 2. The spatial correlation structure for modeling sub-unit level dependence was the Matérn family (6) with parameters ϕ = 8 and ν = 0.1. The error variance was set to be σ² = 0.01.

Setup 2. We used a model with two unit level and two sub-unit level PCs given in (18) and (19) respectively. The unit level PC score variances were ${\sigma }_{\alpha ,11}^2=0.64$ and ${\sigma }_{\alpha ,12}^2=0.25$ for treatment group 1 and ${\sigma }_{\alpha ,21}^2=0.16$ and ${\sigma }_{\alpha ,22}^2=0.04$ for treatment group 2. The sub-unit level PC score variances were ${\sigma }_{\beta ,11}^2=0.36$ and ${\sigma }_{\beta ,12}^2=0.09$ for treatment group 1 and ${\sigma }_{\beta ,21}^2=0.16$ and ${\sigma }_{\beta ,22}^2=0.04$ for treatment group 2. The spatial correlation structure was the Matérn family (6) with parameters ϕ₁ = 8, ϕ₂ = 4, ν₁ = 0.1 and ν₂ = 0.3. The error variance was set to be σ² = 0.01.

Setup 3. This is the same as Setup 2 except that all variance parameters, including PC variances and the error variance, were halved. This setup is equivalent to doubling the sample size of Setup 2. We did not simulate data by doubling the sample size because that would have created a serious computational burden for the Bayesian method.

Next we considered a slight modification of our model where functional data are independent.

Setup 4. This is the same as Setup 2 except that there was no spatial correlation among sub-unit level PCs. We applied our program to this setup to test its performance in a situation it is not designed to handle.

We also considered setups where data were generated from the Bayesian hierarchical models of Baladandayuthapani, et al. (2008). One setup is presented below. The results for two other setups are presented in the supplemental materials.

Setup 5. We used the notation introduced in Section 2.5 where a brief summary of the Bayesian hierarchical model was given. The basis functions corresponding to a three-knot quadratic splines were as in (12) with $m_1(t)=\sqrt{12}(t-0.5)$, $m_2(t)=\sqrt{180}\{{(t-0.5)}^2-1/12\}$ and knot locations t₁ = 0.25, t₂ = 0.5 and t₃ = 0.75. The fixed treatment effects were γ₁ = (1, 0.5, 1.5, 1, −0.8, 0.3)^T and γ₂ = (2, −0.5, −0.3, 1.2, −.4, −0.7)^T. To specify the unit level random effects distribution, we set ${\sigma }_2^2=0.1$ and

$$\begin{array}{ccc}{\displaystyle {\sum }_{21}^{*}=\left(\begin{array}{ccc}1.00& 0.84& 0.18\\ 0.84& 1.44& 0.54\\ 0.18& 0.54& 0.81\end{array}\right)}& \text{and}& {\displaystyle {\sum }_{22}^{*}=\left(\begin{array}{ccc}1.440& 0.756& 0.240\\ 0.756& 0.810& 0.450\\ 0.3240& 0.450& 1.00\end{array}\right)}\end{array}.$$

and to specify the sub-unit level random effects distribution, we set ${\sigma }_3^2=0.1$ and

$$\begin{array}{ccc}{\displaystyle {\sum }_{31}^{*}=\left(\begin{array}{ccc}1.000& 0.240& 0.180\\ 0.240& 1.440& 0.648\\ 0.180& 0.648& 0.810\end{array}\right)}& \text{and}& {\displaystyle {\sum }_{32}^{*}=\left(\begin{array}{ccc}1.000& 0.180& 0.260\\ 0.180& 0.810& 0.702\\ 0.260& 0.702& 1.690\end{array}\right)}\end{array}.$$

The parameters of the Matérn family (6) were set to ϕ = 0.57 and ν = 0.11. The noise variance was set to be σ² = 0.01. We ran our method with three unit and sub-unit level principal components, a specification of our model that provided a reasonable approximation to the simulation model. The Bayesian method encountered some numerical problems and could only run on 78 out of 100 simulated data sets. More serious numerical problems were experienced by the Bayesian method in two setups presented in supplemental materials.

Table 1 shows the results of comparing our reduced rank method with the Bayesian method. For setups 1–4, our reduced rank method consistently did a much better job in estimating the mean functions and in predicting the random effects. The inferior performance of the Bayesian method might be due to its use of oversimplified covariance matrices and/or of a separable covariance structure, it might also be that the Baysian model is overfitting the data. For data generated from the Bayesian model, our reduced rank method is comparable to the Bayesian method. We do not compare the parameter estimates here since parameters from the two models have different interpretations. Some results of parameter estimation for our method are presented in the online supplementary materials.

Table 1.

Comparison of two methods based on 100 simulation runs. Mean (SE) of the integrated absolute errors of estimating the mean functions and predicting the unit and sub-unit level random effects. Numbers shown are the actual numbers multiplied by 10. “Reduced rank” refers to our method; “Bayesian” refers to the Bayesian method of Baladandayuthapani, et al. (2008).

Setup	Method	Mean		Unit		Sub-Unit
1	Reduced rank	1.332	(0.061)	1.361	(0.072)	0.861	(0.051)
	Bayesian	1.945	(0.041)	3.512	(0.046)	1.637	(0.030)
2	Reduced rank	1.633	(0.057)	2.152	(0.097)	1.628	(0.100)
	Bayesian	2.161	(0.046)	3.797	(0.052)	2.051	(0.023)
3	Reduced rank	1.151	(0.040)	1.487	(0.059)	1.117	(0.062)
	Bayesian	1.886	(0.023)	2.681	(0.036)	1.502	(0.016)
4	Reduced rank	1.492	(0.056)	1.517	(0.055)	0.543	(0.014)
	Bayesian	2.049	(0.034)	3.366	(0.046)	1.055	(0.011)
5	Reduced rank	4.170	(0.128)	5.571	(0.094)	4.063	(0.039)
	Bayesian	4.086	(0.146)	5.518	(0.108)	4.104	(0.046)

6 Application to Colon Carcinogenesis Data

In this section we apply our model to the rodent experiment introduced in Section 1. We will focus on studying the cell expression level of the p27 protein, a cyclin-dependent kinase inhibitor in normal and neoplastic cells. These data were analyzed previously by Baladandayuthapani, et al. (2008) using their Bayesian hierarchical model. The data were also used in Li et al. (2008) to illustrate a method for nonparametric estimation of correlation functions.

In the experiment, 48 rats were randomized to 4 diet groups: corn oil with butyrate (CO+B), corn oil without butyrate (CO−B), fish oil with butyrate (FO+B) and fish oil without butyrate (FO−B). After being fed these diets for 2 weeks, each rat was exposed to the carcinogen azoxymethane (AOM) and euthanized at one of four randomly chosen time points: 0, 12 hours, 24 hours and 48 hours. From each rat, 20–30 crypts were selected from its colon and the physical locations of the crypts were measured in microns. Within rat crypt distance ranges from 5 microns to about 14, 000 microns. There are about 20–40 cells on each crypt and their relative cell positions t were calculated such that the bottom of each crypt has t = 0 and the top has t = 1, with positions in between coded proportionally. The expression level of p27 was determined for each cell. For details on the measuring process, see, Hong, et al. (1997). Our goal is to study the phenomenon of crypt signaling, that the level of p27 in the cells in a given crypt is affected by neighboring crypts and the effect is a function of crypt distances.

As an illustration of our methods, we use data from rats euthanized at 24 hours only. We have diet groups as the treatment groups, and each rat is a unit with its crypts as sub-units. In the notation of our model (8) given in Section 2.4, denote Y for the logarithm transformed p27 levels which are standardized to have mean 0 and variance 1, denote X for the crypt location and t for relative cell position. Based on the biological nature of our data and the short length of the assayed colon slice, it is reasonable to assume that cells on nearby crypts would have similar p27 responses and the correlation coefficient function between the crypt level PC scores is stationary in the sense that it only depends on the relative distance between crypts. As mentioned in Section 2.3, we used the Matérn family of isotropic autocorrelation function in our model. For simplicity, the same parameters ϕ and ν are used for all diet groups.

For modeling the diet, rat and crypt level functions of relative cell positions, we used quadratic B-splines with 5 equally spaced interior knots. Three-fold crossvalidation, with rats from each treatment group evenly distributed to each fold, was used both to select the penalty parameters and to determine the number of PCs (Sections 4.1 and 4.2). Crossvalidation scores of some feasible number of PCs are given in Table 2. We decided to use one rat level and two crypt level PC functions because, the crossvalidation score increases significantly if fewer PCs are used and it does not change much if more PCs are used. Various diagnostic plots (Section 4.3, not shown) also confirmed that our choice is reasonable.

Table 2.

The crossvalidation scores for some candidate models.

# of rat level PCs	# of crypt level PCs
	1	2	3	4
1	−608.00	−702.84	−721.70	−725.65
2	170.46	−703.45	−722.52	−728.32

Next we report our analysis results on crypt signaling and diet effects. The parametric bootstrap method was applied with 500 bootstrap samples to estimate the distribution of parameter estimates. When applying the bootstrap, the penalty parameters are reestimated for each bootstrap sample while the number of PC’s is fixed. We fixed the number of PC’s to ensure that model parameters are the same for all bootstrap samples. This may lead to underestimation of the variation, however the effect will only be slight because the method of choosing the number of PCs is almost always correct in our simulations.

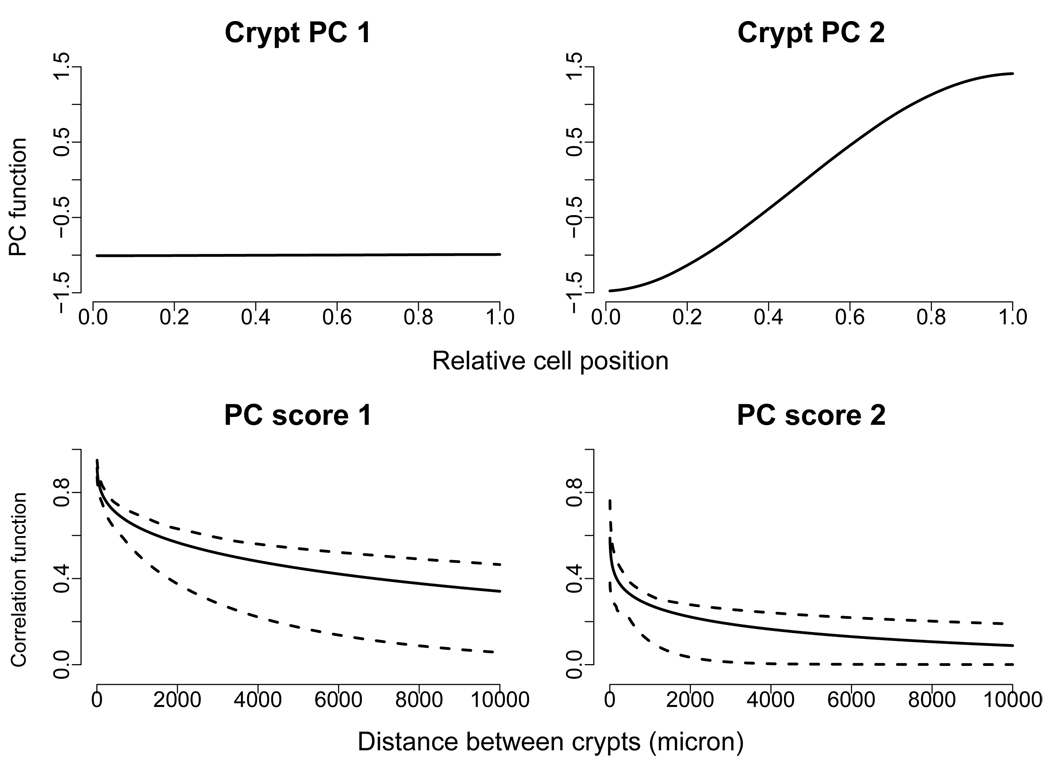
The estimated rat level PC is almost a constant (not shown). The estimated crypt level PC functions are shown on the top panels of Figure 1. For the spatial correlation parameters of the Matérn family, the range parameter ϕ is estimated to be 29.39 and 8.58 with 95% CIs (4.73, 147.39) and (0.74, 76.08) for the two PC scores respectively; the estimated Matérn order ν is 0.13 and 0.05 with 95% CIs (0.10, 0.20) and (0.02, 0.12) respectively. The bottom panels of Figure 1 show the estimated correlation function of crypt level PC scores along with corresponding 95% CIs for crypt distances from 5 to 10, 000 microns. The estimated correlation functions strongly suggest the existence of crypt signaling: cells in crypts that are located close together tend to have similar p27 expression levels; the similarity decreases as the distance between crypts increases. The correlation function of the first PC scores decay slower than that of the second PC scores.

Figure 1.

Colon carcinogenesis data. Top panels: estimated crypt level PC functions. Bottom panels: estimated correlation functions of PC scores over crypt distance and corresponding 90% pointwise confidence intervals.

Baladandayuthapani, et al. (2008) used a separable space-time covariance structure to analyze the same data. Our fitted model suggests a nonseparable covariance structure, because it uses two crypt level PC functions with different correlation parameters and in particular, the 95% CI for ν₁ −ν₂ is (0.02, 0.15). More specifically, following (7) in Section 2.3, for two crypts c and c′ with physical distance d_cc′ from diet group a, rat b, the covariance of the corresponding crypt level functions η_abc(t) and η_abc′(t′) is

$$\text{cov}({\eta }_{abc}(t),{\eta }_{abc\prime }(t\prime ))={\sigma }_{\beta ,a1}^2\rho (d_{cc\prime };{\varphi }_1,v_1)g_1(t)g_1(t\prime )+{\sigma }_{\beta ,a2}^2\rho (d_{cc\prime };{\varphi }_2,v_2)g_2(t)g_2(t\prime ),$$

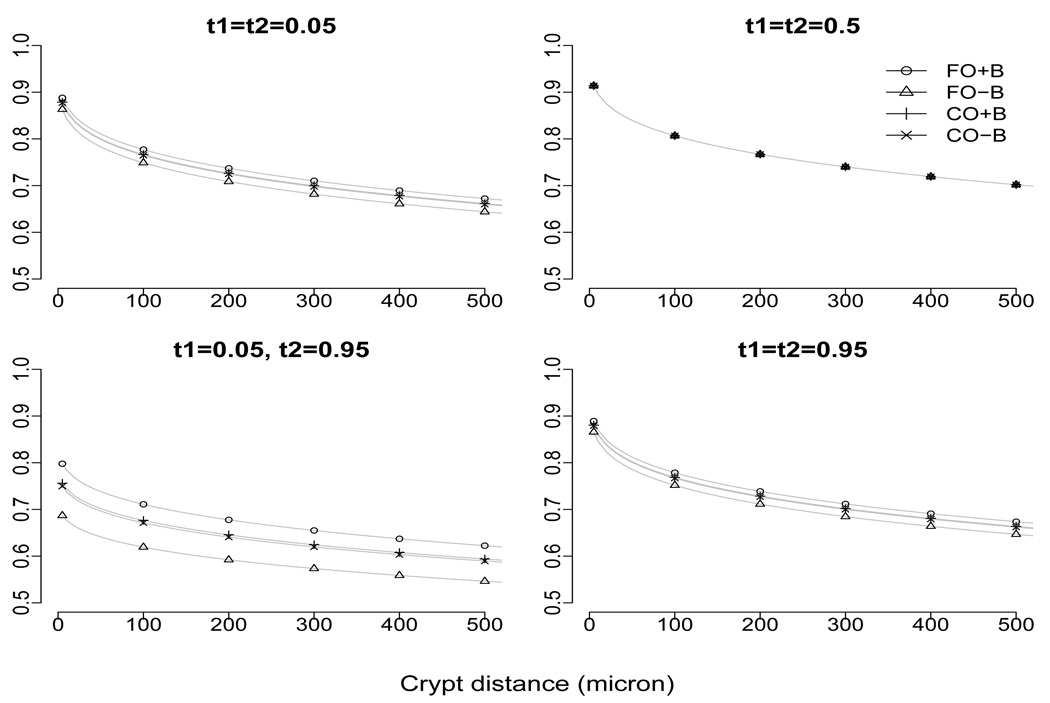
which is nonseparable since ϕ₁ ≠ ϕ₂ and ν₁ ≠ ν₂. Figure 2 plots the fitted correlation functions as a function of physical distance d_cc′ for selected pairs of t and t′. In addition to suggesting crypt signaling, Figure 2 also suggests that the covariance structure is treatment dependent and that the correlation at locations t and t′ from two different crypts is higher when t and t′ are closer.

Figure 2.

Estimated correlation functions over crypt distance for selected combinations of relative cell depth (denoted as t₁ and t₂).

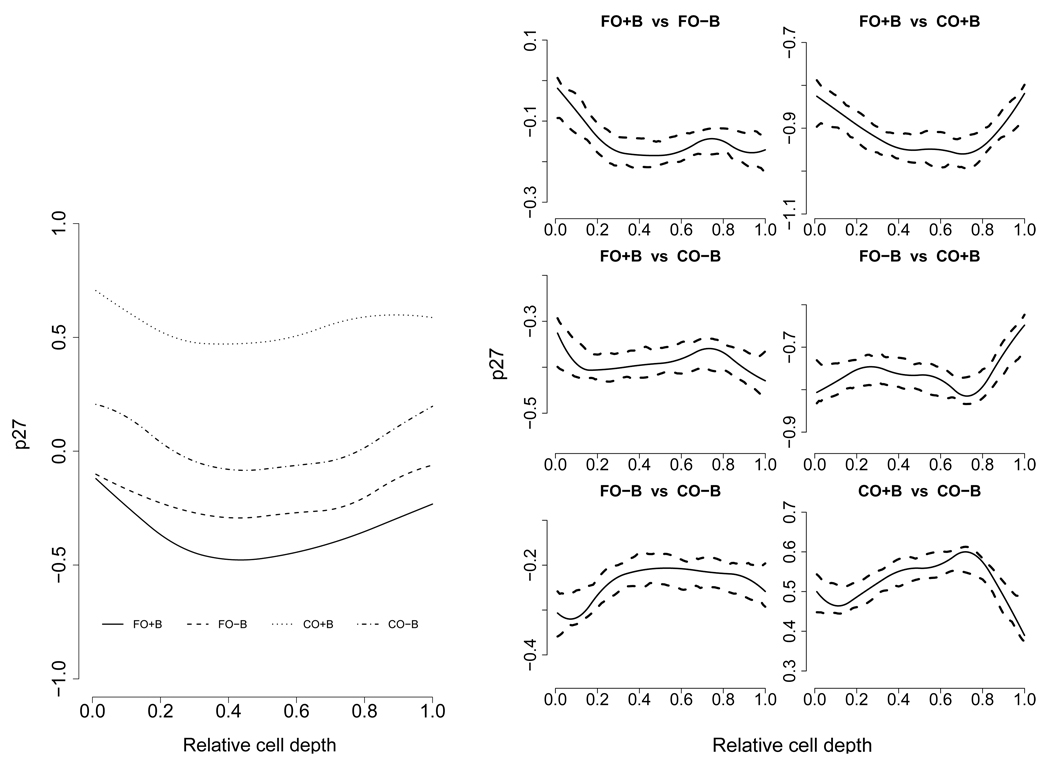
Figure 3(a) shows the mean diet level functions for the four diet groups. There seem to be some diet differences especially between the CO+B diet versus the rest of the diets. To investigate this further, Figure 3(b) shows all pairwise differences between the mean diet level functions of two diet groups, together with corresponding 95% pointwise confidence intervals. All diet groups show significant differences in mean (logarithm transformed) p27 level. Using their Bayesian hierarchical model and pointwise Bayesian credible intervals, Baladandayuthapani, et al. (2008) also found significant difference between the CO+B diet and the other three diets, but not among the later three. Residual plots available in the supplemental materials clearly indicate that our reduced rank model provided better fit to the data than the Bayesian model.

Figure 3.

Estimated mean log p27 level over relative cell depth for the four diet groups. CO is Corn Oil, FO is Fish Oil and with or without (±) Butyrate supplement. The left figure gives the fitted group mean functions. The right figure compares the mean functions with 95% pointwise confidence intervals.

7 Conclusion

In this paper we have proposed mixed effects models for spatially correlated hierarchical functional data. Dimension reduction by principal components plays an important role both in modeling the covariance structure of random functions and in modeling spatial correlation.

Existing work on modeling covariance structure applied diagonal correlation matrices on coefficients in certain fixed basis expansions; Baladandayuthapani, et al. (2008) used truncated power (spline) basis expansions. Our approach also applies diagonal correlation in basis expansion, but the major difference with existing work is that our basis system is determined by data. Note that relaxation of the diagonal restriction to the correlation matrices in the fixed basis approach introduces too many parameters and thus poses substantial statistical and computational challenges. Our use of principal components basis functions provides a flexible, yet feasible approach of modeling the covariance structure. Moreover, instead of modeling the correlation between sub-unit level random effects directly, we model spatial correlation through principal component scores and therefore relax the space-time separability assumption employed by Baladandayuthapani, et al. (2008).