Application of the Pattern-Mixture Latent Trajectory Model in an Epidemiological Study with Non-Ignorable Missingness

Abstract

In longitudinal studies where the same individuals are followed over time, bias caused by unobserved data raises a serious concern, particularly when the data are missing in a non-ignorable manner. One approach to deal with non-ignorable missing data is a pattern mixture model. In this paper, we combine the pattern mixture model with latent trajectory analysis using the SAS TRAJ procedure, which offers a practical solution to many problems of the same nature. Our model assumes a stochastic process that categorizes a relative large number of missing-data patterns into several latent groups, each of which has unique outcome trajectory, which allows patterns with missing values to share information with patterns with more data points. We estimated the longitudinal trajectories of a memory test over 12 years of follow-up, using data from the prospective epidemiological study of dementia. Missing data patterns were created conditional on survival, and final marginal response was obtained by excluding those who had died at each time point. The approach presented here is appealing since it can be easily implemented using common software.

1. Introduction

Longitudinal designs, requiring follow-up of the same individuals over time, are increasingly common in epidemiological studies. However, missing data bias is a major problem in longitudinal studies where attrition is inevitable over time, particularly among older adults. Frail elderly subjects are likely to miss or delay scheduled assessments for a variety of reasons, and a further problem is that the study outcomes themselves are often associated with the frailty (e.g., disability, disease severity).

Restricting analyses to only the observed data could bias the results depending on the types of missingness. Little and Rubin (1987) defined three types of missing-data mechanisms; 1. Missing Completely At Random (MCAR), which literally means missingness is completely random and does not depend on participants’ characteristics, 2. Missing At Random (MAR), where missingness depends on participant’s previously observed responses or observed characteristics, and 3. Missing Not At Random (MNAR), where missingness depends on unobserved outcome values (as well as possibly on observed values). Laird (1988), Little and Rubin (1987) also defined two general classes of missing-data mechanisms for likelihood-based approaches. A missing-data process is called ignorable if a likelihood-based approach provides valid inferences to the model parameters even when the missingness is ignored, while if not, called non-ignorable. Laird (1988) showed that MAR is an ignorable missing-data mechanism. However, under MNAR, likelihood-based analyses that ignore the missing-data mechanism may be biased (non-ignorable missingness).

Two general classes of model based approaches were proposed to cope with non-ignorable missing-data: selection models and pattern-mixture models (Little, 1993). The two models differ in the way the joint distribution of (Y, R) (Y :outcome, R: Missing indicator) is partitioned. Selection models partition the joint distribution of Y and R to be the distribution of Y and the conditional distribution of R given Y as shown below in (1.1), while pattern mixture models partition the joint distribution to be the distribution of R and the conditional distribution of Y given R as shown in (1.2).

$$P(y,r\mid X,\theta )=P(y\mid X,\beta )P(r\mid y,X,\lambda )$$ (1.1)

$$P(y,r\mid X,\gamma )=P(r\mid X,\alpha )P(y\mid r,X,\pi ),$$ (1.2)

where θ = (β, λ) and γ = (α, π).

Since missing values, by definition, cannot be observed, the conditional distribution of R given Y (missing-data process) in selection models need to be based on an assumption which could still hold bias if it is mis-specified. Pattern mixture models do not require specification of missing-data process and the marginal distribution of the response can be obtained by a weighted sum of the distribution within each pattern. However, as with selection models, it is not free from shortcomings; one major problem in pattern mixture modeling approach is non-identifiability, or non-estimable parameters. For example, for a particular subgroup of the sample, if we observe only baseline data and there is no follow-up data at all, we cannot estimate the slope of the trajectory for that group. Two major strategies to deal with the non-identifiability of pattern-mixture models are identifying restrictions (Little, 1993; Thijs et al., 2002; Kennward, Molenberghs and Thijs, 2003) and model simplification (Thijs et al., 2002). The first strategy assumes that the missing variable distribution (Little, 1993) is equal to a function of corresponding identifiable distribution of some other patterns. The second strategy allows different patterns to share certain parameters so that the incomplete patterns can borrow information from patterns with more data points.

In this paper, we offer a practical solution to the non-identifiability problem by using latent trajectory analysis in the framework of pattern-mixture models. Latent trajectory analysis (Nagin, 1999; Roeder, Lynch and Nagin, 1999; Jones, Nagin and Roeder, 2001) identifies latent groups which hold different trajectory patterns. By allowing the probability of being in each latent group to depend on the missing-data patterns, the approach presented here can be viewed as the model simplification described previously. We applied this approach to estimate the longitudinal trajectories of a cognitive test, which taps memory function of individuals, over 12 years of follow-up.

In addition to presenting a practical solution to the non-identifiability problem, we report two additional points of significance. One is the way we created the missing data patterns distinguishing dropout due to death from simple dropout (by living subjects). Another is our estimation of the mean conditional on survival, i.e., when we estimated the marginal mean of the response over time by weighted sum of parameters from each missing data pattern, we included only the survivors at each time point. Below we describe first the data, and second the latent trajectory analysis. Then we describe the missing-data patterns, and the approach used to produce the mean trajectory over time, followed by the results and the implication of this approach.

2. Methods

2.1 Data

The Monongahela Valley Independent Elders Survey (MoVIES project) was a prospective epidemiological study of dementia from 1987 to 2002, set in the mid-Monongahela valley of southwestern Pennsylvania. The study background and methods have been reported previously in greater detail (Ganguli et al., 1993; Ganguli et al., 2000). Briefly, the sample was selected by means of a 1:13 age-stratified (65–74, 75+), random sample of elderly individuals in 1987, identified through the voter registration lists. Entry criteria included age 65 years or older, being community-dwelling at the time of study entry, fluency in English, and at least a sixth-grade education. The last two conditions were designed to enhance interpretability of the neuropsychological tests. After giving informed consent, participants were interviewed by trained research associates. Study procedures were approved annually by the University of Pittsburgh Institutional Review Board. 1422 subjects randomly selected from the voter registration list were assessed at study entry (Wave 1, 1987–1989). At approximately two-year intervals thereafter, subjects were re-evaluated in a series of data collection waves. The assessment included cognitive testing with a battery designed to tap a range of cognitive domains affected by dementia. Here we focus on a memory test, the Word List Delayed Recall (WLDR)(10-item version developed for the Consortium to Establish a Registry for Alzheimer’s Disease (Morris et al., 1989). We estimated the mean trajectory on WLDR from Wave 1 (baseline) through Wave 6, over 12 years of follow-up, for the entire cohort, and also separately for age groups 65–75 and 75+ years, adjusting for non-ignorable missing-data bias.

2.2 Latent class trajectory analysis

Trajectory analysis assumes heterogeneity in a sample where unobserved homogeneous sub-populations exist (Nagin, 1999). For example, we expect memory functions overall to decline over time among elderly populations. However, within such a population, there may be subgroups with different slopes, i.e., some individuals who decline more, others who decline less, and yet others who show almost no decline over time. In this example, if we use a linear regression model, the coefficient of a time indicator variable would indicate the amount of decline in memory score as follow-up time increases by 1 unit. We could also add time², or time³, etc. to the model to capture the slope more precisely. There could be as many distinct coefficients, i.e., slopes, as there are subjects. We assume there are clusters (latent groups) which most efficiently categorize these different patterns in slopes (trajectories). In many past studies, the identification of latent groups preceded the identification of risk factors or characteristics associated with each cluster (e.g., in the previous example, higher educational attainment might be associated with the group showing minimal memory decline). However, this approach, where classification of slopes and risk factor analyses are conducted separately, does not account for the uncertainty involved in a classification of slopes, and could thus lead to bias (Clogg 1995; Roeder, Lynch and Nagin, 1999). In the current study, we used the SAS TRAJ procedure (Jones, Nagin and Roeder, 2001). Briefly, this procedure estimates two models simultaneously by using Maximum Likelihood Estimation approach; one estimating the probability of being in each homogenous latent group, identification for each subject based on the time-independent covariates (characteristics of the subject), and the other estimating the trajectory (slope) of each homogeneous group over time. The risk factors (covariates) affect the likelihood of a particular data trajectory, but it is assumed that nothing more can be learned about the data (Y) from risk factors (Z), given group identification (C). Given that there are K latent trajectory groups, the conditional distribution of the observable outcome for subject i (y_i), given risk factors z_i, is written as follows:

$$f(y_i\mid z_i)=\sum _{k=1}^{K}Pr(C_i=k\mid Z_i=z_i)Pr(Y_i=y_i\mid C_i=k),$$

where C_i is latent group identification for subject i.

In this paper, we included missing-data patterns in covariates (Z) along with other covariates potentially affecting longitudinal trajectory of cognitive test performance over time. The effect of time-independent covariate on group membership is modeled with a generalized logit function,

$$Pr(C_i=k\mid Z_i=z_i)=\frac{exp({\theta }_k+{\gamma }_k^{\prime }{z}_i)}{{\sum }_{\ell =1}^{K}exp({\theta }_{\ell }+{\gamma }_{\ell }^{\prime }{z}_i)}.$$

PROC TRAJ also allows time-dependent covariates (Jones, Nagin and Roeder, 2001), which we do not discuss here. In this study, our response variable is WLDR test scores over time. PROC TRAJ provides the option of modeling three different distributions for Pr(Y_i = y_i|C_i = k): count, psychometric scale, and dichotomous data. Since WLDR scores range from 0 to 10, we used a censored normal distribution. The Bayesian Information Criterion (BIC) (Schwarz, 1978) in the SAS TRAJ procedure identified the optimal number of trajectories, along with the polynomial degree of each trajectory. The SAS TRAJ procedure calculates the probability of each subject belonging to each latent group and assigns each subject to the latent group with the largest probability. Parameters were estimated by a maximum likelihood approach using a general quasi-Newton maximization procedure. Subjects with missing longitudinal data are included as long as they have risk factor covariate data. In this study, all subjects have the information on covariates, which are age at baseline, sex, education levels, and missing-data patterns (described below).

2.3 Creation of missing data patterns

Our general observation and past research (Ganguli, Dodge and Mulsant, 2002; Ratcliff et al., 2003; Dodge et al., 2003; Whyte et al., 2004) suggest that those with frail health or low cognition are more likely to miss scheduled assessments. Also we expect that those with sharply declining cognitive status, e.g., due to dementia, could miss all subsequent assessments, regardless of their previously observed cognitive test scores, indicating non-ignorable missing-data. Pattern mixture models can give unbiased estimates under the non-ignorable missing process (Little, 1993) and are used in various applications (e.g., Hedeker and Gibbons, 1997; Park and Lee, 1999). An example of creating missing data patterns is depicted in Table 1. For this illustration, we assume there are baseline and two follow-up data points. A conventional way of creating the missing data patterns is to distinguish the four patterns (completers, missing the last observation only, missing the last two observations, and intermittent missingness) by using three dummy variables. However, it can be informative to distinguish those who survive but drop out of the study from those who miss the interview due to death. If we are interested in the marginal distribution of memory test scores over time, it should be estimated conditional on survivorship of the study participants.

Table 1.

Conventional Way of Missing Data Classification: O=observed, X=missing.

Missing Data Pattern	Wave 1	Wave 2	Wave 3
1 Completers	O	O	O
2 Miss the last observation.	O	O	X
3 Miss the last 2 observations.	O	X	X
4 Intermittent missingness	O	X	O

We created missing patterns based on the data collection wave during which the participants died and the wave at which the last observation was made. Table 2 shows these patterns. We have baseline and five time points of follow-up for a total of 6 observations. The table is read as follows. The subject who died between Wave 1 and Wave 2, with observed cognitive test score at Wave 1 (i.e., missing wave 2 data) is identified under missing data pattern 1. The subject who died between wave 2 and wave 3, with the last observed cognitive test score at wave 1, is identified as missing data pattern 2. The subject who died between wave 2 and wave 3, with the last observed cognitive test at wave 2, is identified as missing pattern 3. Likewise, pattern 9, for example, indicates those who died between wave 4 and wave 5, with their last observed cognitive data at wave 3. Score at wave 2 is not necessarily observed for pattern 9. Here we assume that intermittent missingness occurs randomly due to subjects’ vacation, occasional sickness, family gatherings, etc and do not further distinguish them. This way, we have 21 patterns.

Table 2.

Data missing pattern (Pn) conditional on death

The wave after which participants died	The last observed wave (number of subjects)
	1	2	3	4	5	6
1	Pn 1 (77)
2	Pn 2(30)	Pn 3(71)
3	Pn 4(15)	Pn 5(34)	Pn 6(61)
4	Pn 7(19)	Pn 8(6)	Pn 9(34)	Pn 10(67)
5	Pn 11(14)	Pn 12(5)	Pn 13(13)	Pn 14(40)	Pn 15(65)
6	Pn 16(81)	Pn 17(43)	Pn 18(30)	Pn 19(57)	Pn 20(84)	Pn 21(414)

Pn: Pattern for short, Pattern A is shown with large bold font, Pattern B is shown with bold font, Pattern C is shown with regular font.

Preliminary analysis showed that the trajectory model with covariates distinguishing these 21 patterns was not stable. We, therefore, collapsed these patterns into the three groups based on the observations and impressions by research staff as follows. Those who participate without any missing data up until they die have relatively good cognition, and death is often due to acute illness. However, those who miss out on assessments continuously before they die have relatively poor cognition possibly related to dementia or other chronic diseases affecting cognition. The patterns with large bold font in Table 2 (patterns 11, 16, 17, henceforth called Pattern A) are those who only died after wave 5 or 6, yet had missing memory scores even at early waves such as waves 1 and 2. We expect that these subjects’ memory scores would have been relatively poor at baseline and at follow-ups if we had been able to observe them. The patterns with regular font (patterns 1, 3, 6, 10, 15, and 21, henceforth called Pattern C), on the other hand, represent participants who had memory test scores up until they died. We expect these subjects have relatively high cognition at baseline and follow-ups. The pattern with regular sized-font falls in between the two groups (hence forth called Pattern B). We created two dummy variables to identify the three groups of missing data patterns (Patterns A, B, and C: Pattern A as a reference group) and examined the association between these patterns and baseline memory test scores. In addition, the two dummy variables for patterns A, B and C as well as three basic demographic variables (age at Wave 1, sex, and education — high school graduates or higher education vs. less than high school education) were included in the SAS TRAJ procedure to identify the homogeneous latent trajectory groups of memory test scores over time.

2.4 Estimation of marginal trajectory over time

The trajectory analysis assigns to each individual the probability of falling into each latent trajectory group. Each latent trajectory has its own intercept, linear and quadratic parameters to indicate the trajectory of the memory test score as a function of duration from baseline. By using each subject’s probability of falling into each trajectory group and each trajectory group’s parameter estimates, we calculated subject-specific intercept, linear and quadratic parameters (weighted sum of parameter estimates for each trajectory group). Finally we estimated mean memory test scores as a function of duration from baseline, by averaging the test scores among surviving individuals at each time point (exclude those died from the estimation) using the subject-specific parameter estimates. Confidence intervals of this mean trajectory was computed by using bootstrap (Davison and Hinkley, 1997).

3. Results

To see the trajectory of test score over time among those who were cognitively healthy at baseline, we excluded 126 subjects who were already demented at baseline and 36 subjects who did not complete the WLDR test at baseline. Table 2 shows that 414 subjects (33%, Pattern 21) completed all the 6 observations. Patterns 1, 3, 6, 10, 15 and 21 are for those who completed the test and then died during the same wave. The mean (SD) age, the proportion of women and those with high school education and over, and cognitive test scores among all remaining 1260 subjects at baseline and also among those with each missing data pattern are presented in Table 3. As we expected, those with pattern C (those with memory data right before they died) had highest baseline test scores and showed narrower standard deviation, while those with pattern A (those with missing memory data several waves before they actually died) had the lowest test scores and wider standard deviation, suggesting that this group is more heterogeneous in baseline test scores.

Table 3.

Demographic characteristics of the sample; overall and by missing data patterns

	N	Mean age (SD)	% of women	(A)	(B)
Overall Sample	1260	73.1 (5.72)	56.0	56.8	6.29 (1.99)
Missing pattern A	138	72.9 (5.30)	54.4	48.6	5.86 (2.13)
Missing pattern B	367	73.9 (5.79)	57.2	56.1	6.07 (2.04)
Missing pattern C	755	72.8 (5.74)	55.8	58.7	6.49 (1.92)

(A)= % of those with high school graduate and over, (B)= Mean (SD) baseline memory score (Word List Delayed Recall).

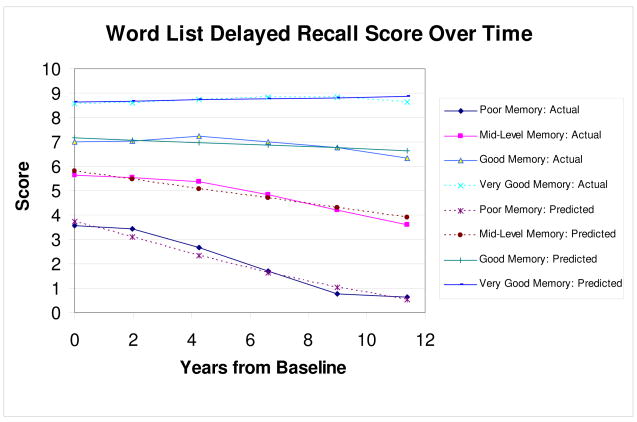
Based on the Baysian Information Criteria (BIC), we identified four latent trajectories. Figure 1 shows these trajectories. Two trajectories are shown for each latent group; a trajectory using subject-specific probabilities belonging to each latent group (indicated as “Actual”) and a trajectory using an assigned latent group for each subject, which is the latent group with the largest probability (indicated as “Predicted”). Each trajectory showed relatively stable patterns over time; we call these 4 groups as 1. poor memory, 2. mid-level memory, 3. good memory, and 4. very good memory. To examine our hypothesis that those who with missing memory test data many years before they died have relatively poor memory test scores at baseline and follow-ups, we calculated the distribution of the latent group membership for each missing data pattern (patterns A, B, and C) for four demographic groups (men and women with higher and lower education). Table 4 shows the results. As we expected, subjects with missing pattern A (those with missing memory data several waves before they actually died; patterns with regular font in Table 2) showed higher probability of belonging to the poor memory group compared with other missing data patterns, while subjects with missing pattern C (those with memory data right before they died) showed higher probability of belonging to the very good memory group. In all four demographic groups, this pattern was clearly seen from Table 4. For example, among men with lower education, 20% of those with missing data pattern A fell into the poor memory latent group, but only 8% of those with missing data pattern C fell into this group. On the other hand, only 1% of those with missing data pattern A fell into the very good memory latent group, but 4% of those with missing data pattern C fell into this group.

Figure 1.

Trajectories of word list delayed recall score for four latent groups

Table 4.

Probability of belonging to each latent group by missing data patterns

	Latent 1	Latent 2	Latent 3	Latent 4
	Poor memory	Mid-level memory	Good memory	Very good memory
Men with lower education
Pattern A	0.20	0.36	0.43	0.01
Pattern B	0.16	0.43	0.38	0.02
Pattern C	0.08	0.42	0.45	0.04
Men with higher education
Pattern A	0.12	0.25	0.60	0.02
Pattern B	0.10	0.30	0.53	0.07
Pattern C	0.04	0.27	0.57	0.11
Women with lower education
Pattern A	0.10	0.29	0.57	0.03
Pattern B	0.08	0.33	0.48	0.11
Pattern C	0.03	0.29	0.50	0.18
Women with higher education
Pattern A	0.05	0.18	0.69	0.08
Pattern B	0.04	0.19	0.54	0.24
Pattern C	0.01	0.14	0.50	0.35

We also compared the results of PROC TRAJ with and without missing data patterns as covariates; we calculated individual specific trajectory (i.e., intercept, linear and quadratic terms) for subjects aged 75 years old with different combinations of sex, education and missing data patterns. The results are shown in Table 5. Here we call PROC TRAJ with covariates of missing data patterns Model 1 and PROC TRAJ without including missing data patterns (i.e., ignoring missingness) Model 2. Model 2 had higher intercepts and higher positive linear trends compared with Model 1 in all groups. One of the marked differences is that in Model 1, men with lower education with missing data patterns A and B had negative linear slopes, while in Model 2 (PROC TRAJ without missing data patterns) the slope was positive. Ignoring missingness could cause bias in our data.

Table 5.

Comparison of the individual specific trajectory based on PROC TRAJ with missing data patterns (indicated as Model 1) and without missing data patterns (indicated as Model 2) as covariates.

Sex	Education	MDP	Intercept		Linear		Quadratic
			Model 1	Model 2	Model 1	Model 2	Model 1	Model 2
Men	Lower	A	5.032	5.547	−0.021	0.009	−0.020	−0.018
		B	5.166		−0.013		−0.019
		C	5.527		0.017		−0.018
	Higher	A	5.364	5.996	0.011	0.038	−0.018	−0.017
		B	5.494		0.016		−0.018
		C	5.854		0.043		−0.017
Women	Lower	A	5.469	6.077	0.017	0.040	−0.018	−0.016
		B	5.628		0.022		−0.018
		C	5.979		0.046		−0.016
	Higher	A	5.828	6.650	0.048	0.068	−0.017	−0.015
		B	6.103		0.052		−0.016
		C	6.490		0.071		−0.014

MDP = Missing Data Pattern for short

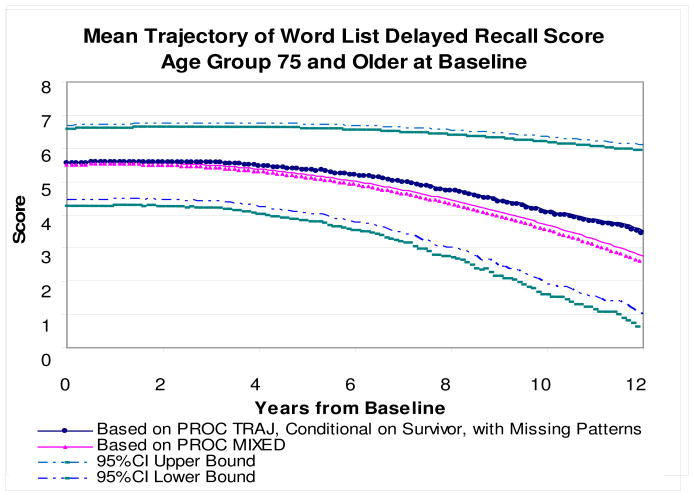
Based on the individual specific parameter estimates derived from trajectory model with missing data patterns as covariates, we then estimated cognitive scores for each individual at continuous time points, excluding those died at each time point, and plotted the trajectory for the whole cohort in Figure 2, and the trajectories among those aged 65 to 75, and those aged 75 and older in Figures 3 and 4, respectively. The confidence interval was calculated for the latent trajectory model through bootstrap approach. Figures 2, 3, and 4 also include the trajectory plots based on the mixture model without missing data patters as covariates, using PROC MIXED (i.e., model under MAR assumption). Since the trajectories based on PROC MIXED do not exclude those dropped out due to death, and subjects who dropped out due to death tend to have sharper declines, the trajectory based on PROC MIXED showed larger decline than those estimated from latent trajectory models which used only survivors at each time point. Since PROC MIXED ignores the non-ignorable missingness, it usually tends to underestimate the decline, but the figures presented here indicate that the inclusion of dead people has a large impact on the overall marginal trajectories.

Figure 2.

Mean trajectory of word list delayed recall score: whole cohort

Figure 3.

Mean trajectory of word list delayed recall score: age group 65–75 at baseline

Figure 4.

Mean trajectory of word list delayed recall score: age group 75 and older at baseline

4. Conclusion

In longitudinal data, we often encounter non-random missingness. The pattern mixture model approach treats the whole population as a mixture of several patterns of respondents and non-respondents and estimates overall population parameters by weighted-averaged across patterns. Although pattern mixture model has the advantage of not requiring the assumption of missing-data process, one problem is non-identifiability. Here we used the latent trajectory approach which is incorporated in SAS PROC TRAJ. This approach avoids the problem of non-estimable parameters pertained in pattern mixture model by allowing patterns with missing values to share information with patterns with more data points through the latent variable. Our approach can be viewed as a model simplification, similar in a way to that of Roy (2003), who used latent class analysis to reduce large numbers of missing data patterns. The approach presented in this paper estimates two models simultaneously by using Maximum Likelihood Estimation procedure; one for estimating the probability of being in each latent group given covariates, and another estimating the trajectory of each latent group. The missing data patterns were included as covariates to take care of the bias under the assumption of non-ignorable data missingness.

One added significance is the way we created missing data patterns; we distinguished those who dropped out due to death from those who dropped out for other reasons while still alive, creating missing data patterns based on the number of waves missed before death. Final marginal response of outcome over time was estimated by excluding those who died at each time point, making the results representative among survivors. The trajectory based on PROC MIXED could over-adjust the slope by extrapolating the estimates beyond subjects’ death. If the goal of obtaining the trajectory is to show the mean scores among the subjects who survived at each time point, then caution is needed to ensure the estimates reflect those among survivors.

One limitation of the approach presented here is that we collapsed large number of missing-data patterns into feasible numbers of patterns based on our hypothesis and assumptions. There could be heterogeneity within the collapsed missing data patterns. Also as with other missing data models, we cannot test that missing data are MAR within dropout patterns. One of the advantages of the approach used here is that SAS TRAJ is easily run in SAS (the macros obtainable from the website: http://www.andrew.cmu.edu/user/bjones), which makes it appealing for the applications in various fields. Characteristics of non-respondents could differ depending on the nature of the study (e.g., Veenstra et al., 2006). Creation of missing data patterns based on the careful examinations of factors potentially associated with non-response or non-response patterns, together with the latent trajectory analysis could give a flexible solution to non-ignorable missingness in a longitudinal study. Our approach should be useful to investigators analyzing data from repeated measures over long periods of time, particularly in population-based observational studies where attrition is inevitable.