One-Dimensional Brownian Motion of Charged Nanoparticles along Microtubules: A Model System for Weak Binding Interactions

Abstract

Various proteins are known to exhibit one-dimensional Brownian motion along charged rodlike polymers, such as microtubules (MTs), actin, and DNA. The electrostatic interaction between the proteins and the rodlike polymers appears to be crucial for one-dimensional Brownian motion, although the underlying mechanism has not been fully clarified. We examined the interactions of positively-charged nanoparticles composed of polyacrylamide gels with MTs. These hydrophilic nanoparticles bound to MTs and displayed one-dimensional Brownian motion in a charge-dependent manner, which indicates that nonspecific electrostatic interaction is sufficient for one-dimensional Brownian motion. The diffusion coefficient decreased exponentially with an increasing particle charge (with the exponent being 0.10 k_BT per charge), whereas the duration of the interaction increased exponentially (exponent of 0.22 k_BT per charge). These results can be explained semiquantitatively if one assumes that a particle repeats a cycle of binding to and movement along an MT until it finally dissociates from the MT. During the movement, a particle is still electrostatically constrained in the potential valley surrounding the MT. This entire process can be described by a three-state model analogous to the Michaelis-Menten scheme, in which the two parameters of the equilibrium constant between binding and movement, and the rate of dissociation from the MT, are derived as a function of the particle charge density. This study highlights the possibility that the weak binding interactions between proteins and rodlike polymers, e.g., MTs, are mediated by a similar, nonspecific charge-dependent mechanism.

Introduction

Various microtubule-associating proteins, including dynein, dynactin, KIF1A, and MCAK, exhibit one-dimensional Brownian motion along microtubules (MTs) (1–7). In the case of motor proteins, one-dimensional Brownian motion is thought to occur in the weak binding state of the normal ATPase cycle, and may contribute to generate its translational movement (8–13). The stability of this one-dimensional Brownian motion appears to be dependent upon the electrostatic interaction between the positive charges on these proteins located at the interface with tubulin and the negatively-charged C-terminal region of tubulin (4,5,14).

Previously, we have shown that MTs have high conductivities owing to counterion polarization; the counterions condensed on the surface of the negatively-charged MT are mobile along the MT long axis (15). Similarly, proteins with a sufficient number of positive charges appropriately exposed on their surfaces may interact electrostatically with MTs, while retaining their freedom of motion along the MT long axis. Indeed, one-dimensional Brownian motion is observed not only for MT-based motor proteins, but also for other combinations of charged polymers and their partner proteins. For example, a number of DNA binding proteins are known to exhibit one-dimensional Brownian motion along DNA filaments (16–20), and the motor protein myosin displays Brownian motion along actin filaments (21–23). More surprisingly, myosin V can move along an MT filament using Brownian motion, even though it is intrinsically an actin-based motor protein (24). This observation suggests that one-dimensional Brownian motion is electrostatic in origin and is not reliant on unique tertiary structures. Thus, it should be possible for any charged molecule or particle to bind to and move along an MT.

In this study, we tested this hypothesis using nanoparticles composed of polyacrylamide gel. Noncharged nanoparticles did not interact with the MTs, whereas nanoparticles that were functionalized with amino groups showed undirected one-dimensional Brownian motion along the filaments, indicating that one-dimensional Brownian motion is based on nonspecific electrostatic interactions. By quantifying the diffusional movements of these nanoparticles with variable amine densities, we dissected the elementary processes involved in one-dimensional Brownian motion. The results of our analyses indicate that one-dimensional Brownian motion of a nanoparticle comprises two phases: 1), the stationary binding of the nanoparticle to the MT; and 2), free movement of the nanoparticle along the potential valley of the MT.

Materials and Methods

Preparation of MTs and positively-charged polyacrylamide nanoparticles

MTs containing 13 protofilaments were prepared from pig brains, as described previously (15). Polyacrylamide nanoparticles with different levels of amine modification were synthesized following the previously published protocol (25,26; see Methods in the Supporting Material for details). These positively-charged particles of heterogeneous sizes (1–100 nm) were fractionated by sucrose density gradient centrifugation (10–50% sucrose, 36,000 × g, 16.5 h, 4°C). The diameters of the particles in solution were determined by transmission electron microscopy (JEM-2000ES; JEOL, Tokyo, Japan) of negatively-stained images, taking the effect of flattening into consideration. A fraction with an average diameter of 57 ± 13 nm was used for the experiments (see Fig. 1 and Methods in the Supporting Material for measurement details).

Figure 1.

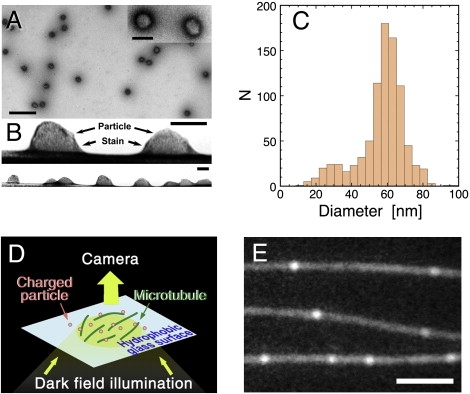
Preparation of the charged nanoparticles and the experimental system used for observations of the particle-MT interaction. (A) Negatively-stained image of polyacrylamide particles after fractionation via sucrose density gradient centrifugation. Bar = 500 nm. (Inset) Magnified view (bar = 100 nm). The aspect ratio of the particle (ratio of major to minor axis) was 1.13 ± 0.13 (mean ± SD, n = 865), indicating that particles can be regarded as spheres rather than ellipsoids. (B) A side view of the particles showing their flattening on the charged surface of the carbon film (bar = 100 nm). Such side views were obtained from a few accidental occasions where the carbon film was torn and curved. Based on such images, a ratio of equatorial radius to height, a measure of shape flattening, was calculated to be 1.27 ± 0.16 (n = 11). (C) Distribution of the particle diameters for a fraction of particles with an amine density 0.96 nm⁻³, after correction for shape flattening. The average of the diameters was 57 ± 13 nm (mean ± SD, n = 865). For details of the diameter measurement, see Fig. S1 and Methods in the Supporting Material. (D) Interactions between charged nanoparticles and MTs were observed by DFM. To eliminate the electrostatic interactions of particles or MTs with the glass surface, MTs were attached to a hydrophobically modified glass surface (see Materials and Methods for details). (E) A representative DFM image of nanoparticles interacting with MTs. Bar = 3 μm.

Determination of amine density

The amine density of particles, ρ, was calculated based on the relationship ρ = C_NH2/(v_p × n_p), where C_NH2 is the amine concentration of the suspension, n_p is the number concentration of particles, and v_p is the average volume of particles. C_NH2 was determined by the TNBS method (27). Both n_p and v_p were measured from negatively stained images of the nanoparticles. Based on the size distribution of the particle (Fig. 1 C), the average volume v_p was calculated as 1.1 × 10⁵ nm³. By combining the data for C_NH2, v_p, and n_p, ρ was calculated to be 0.3–0.96 nm⁻³, depending on the extent of amination (Table 1). Standard deviation (SD) was derived as the sum of the errors for each measurement of C_NH2, v_p, and n_p. By measuring the light scattering (λ = 250 nm) of a particle solution with a known n_p, the extinction coefficient of the nanoparticle was determined to be 5.14 × 10⁸ cm⁻¹ M⁻¹ (DU640 spectrophotometer; Beckman, Fullerton, CA). Subsequently, n_p was simply deduced from the intensity of the light extinction of the solution.

Table 1.

Polyacrylamide nanoparticle characteristics

Reaction time of amination [h]	Amine density ρ [nm−3] (mean ± SD)	Net charges/ particle∗ (×103)	Number of effective charges, Q∗ (mean ± SD)	Diameter of particles subjected to the analysis of motion† [nm] (mean ± SD)
1.3	0.30 ± 0.05	33	13 ± 2	61 ± 6
2.0	0.36 ± 0.06	40	15 ± 3	62 ± 5
3.0	0.55 ± 0.10	60	24 ± 4	57 ± 4
4.0	0.59 ± 0.11	65	26 ± 5	58 ± 5
5.0	0.73 ± 0.13	80	32 ± 7	59 ± 5
7.0	0.96 ± 0.17	106	42 ± 11	60 ± 5

^∗These numbers are for the particles subjected to motion analysis.

^†For details of diameter measurements under DFM, see Methods and Fig. S2.

Observation of the particle-MT interaction

For observation of the particle-MT interaction, a flow cell composed of two coverslips (dimensions: 7 × 7 × 0.15 mm) was prepared, in which the bottom wall (dimensions: 24 × 32 mm) was silanized with 1.2% 3-methacryloxypropyltrimethoxysilane solution (LS-3380; ShinEtsu Chemicals, Tokyo, Japan). A 7-μL aliquot of MT solution (10 μM of MT in BRB80 buffer that contained 80 mM MES (pH 6.8), 2 mM MgCl₂, 1 mM EGTA, 10 μM paclitaxel) was introduced into the flow cell. After 1 min of incubation, the cell was extensively washed with ∼70 μL (equivalent to 10 volumes of the flow cell) of the observation solution (30 mM MES (pH 6.8), 0.3 mM MgCl₂, 25 mM KCl, 10 μM paclitaxel, 0.003% (v/v) NP40). Subsequently, 10 μL of polyacrylamide nanoparticles were introduced and the cell was sealed using Vaseline, to prevent evaporation of the solution. The particle concentrations were optimized for each type of experiment (Table S1) to ensure the accuracy of counting in the binding assay (Fig. 2 A), or to avoid collisions between the particles (Fig. 2, B–E, and Fig. 3). The solution did not contain any proteins, such as casein or bovine serum albumin (to block nonspecific binding of the particles to the glass surface), because they might also bind to the particles, thereby introducing hydrophobic groups or additional charges onto the surfaces of the particles. To prevent nonspecific binding of the particles to the glass surface without using blocking reagents, the bottom wall of the flow cell was made slightly hydrophobic by silanization, and the ionic strength of the solution was carefully optimized. To prevent denaturation of the MTs on the hydrophobic glass surface, NP40 was included in the solution. It was confirmed in an independent experiment that NP40 did not essentially affect the interactions between the nanoparticles and the MTs.

Figure 2.

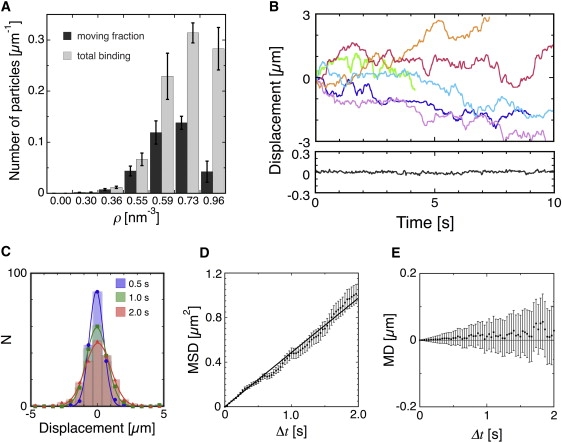
Interaction of the charged nanoparticles with the MTs. (A) Binding of charged nanoparticles to the MTs examined by DFM. The total number of particles on the MTs (shaded) and the number of moving particles (solid) per unit length of the MTs are plotted as a function of the amine densities of the particles. One minute after the particle suspension was introduced into the flow cell, 9–18 fields were scanned within 5 min and their images were recorded for later analysis. For each MT, the numbers of moving (SD ≥ 30 nm) and stationary (SD < 30 nm) particles during a single 10-s observation period were counted. The numbers of moving/stationary particles on MT lengths of 300–800 μm were summed, normalized for the particle concentration used in each experiment (Table S1) and divided by the MT lengths, which gave the number of bound/moving particles per unit length of MT. (B) Examples of the back-and-forth movements of the charged particles along the MTs. Each trace shows the track of an individual nanoparticle with amine density of 0.59 nm⁻³. The upper and lower panels show the motions parallel and perpendicular to the long axes of the MT, respectively. In the upper panel, displacement in the plus direction corresponds to motion toward the MT-plus end. (C) Distributions of the particle displacements in 0.5-, 1.0-, and 2.0-s intervals. (D) MSD and (E) mean displacement of the particles plotted against time. The error bars represent mean ± SE.

Figure 3.

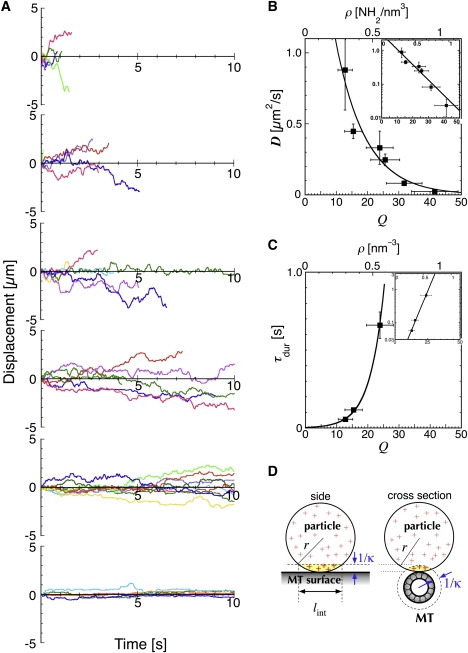
Analysis of one-dimensional Brownian motion. (A) Typical traces for the displacements of particles with amine densities of (from the top downwards) 0.30, 0.36, 0.55, 0.59, 0.73, and 0.96 nm⁻³. (B) Diffusion constant of the particle, D, plotted against ρ or Q. D is the average of more than five independent diffusion constants, each calculated from an MSD plot for >10 particles over a total sampling time of 20 s. The error bars in the vertical and horizontal axes represent SD. The diffusion constant D appears to be an exponential function of Q, i.e., the data show good fit to the equation:$D/D_0=e^{-Q\Delta E_1/k_{\text{B}}T},$ where D₀ = 3.0 μm²/s and ΔE₁ = 0.10 k_BT per charge (inset). (C) Mean duration of the interaction plotted against ρ or Q. The error bars represent standard error of fit (vertical axis) and SD (horizontal axis). The data show good fit to the equation:$\tau {}_0/{\tau }_{\text{dur}}=e^{-Q\Delta E_2/k_{\text{B}}T},$ where τ₀ = 3.6 ms and ΔE₂ = 0.22 k_BT per charge (inset). (D) Q was calculated based on the amine density of the particle (ρ), radius of the particle and MT, and the Debye length (κ⁻¹ = 1.29 nm). For a particle of diameter 59 nm, Q = 43.2 × ρ, and l_int = 17 nm (see Materials and Methods for details).

Interactions of the particles with the MTs were observed by dark-field microscopy (DFM) (BX100; Olympus, Tokyo, Japan) using a 100× oil-immersion lens (UPlanFL N; Olympus) and a 100-W mercury-arc lamp (USH-102D; Ushio, Tokyo, Japan). Images were obtained using a charge-coupled device camera coupled to a GaAsP image intensifier (C8600, C3077-70; Hamamatsu Photonics, Hamamatsu, Japan) and stored in a videocassette recorder at 30 frames/s. All experiments were performed at 25 ± 0.5°C. The MTs were stable for >2 h under these experimental conditions, and the observations were completed within 15 min of the introduction of the MTs into the flow cell. To examine the directional bias of the Brownian motion (Fig. 2), an experiment was performed using a special type of flow cell, which was designed to prevent evaporation of the solution without Vaseline sealing. At the end of each experiment, kinesin-coated latex beads (28) and ATP were introduced into the flow cell and the polarity of the MT used in the experiment was determined by the direction of kinesin movement.

Analyses of particle movements

Image analysis was performed on a personal computer using the Scion Image software (Scion, Frederick, MD) with home-made macro programs. The zoom settings of the microscope and camera system resulted in a pixel size of 40 nm. To determine the position of a particle with subpixel accuracy, a rectangular subregion of 25 × 25 pixels was first extracted from each video frame, with its center positioned on the brightest pixel in the particle, and the intensity-weighted centroid of this subregion was calculated. The standard deviation for the positions of the particles that were rigidly attached to the glass surface was 25 nm (at the video rate), indicating that spatial resolution in the subpixel size range was achieved. To record the position of the particle along the MT, the x and y coordinates of the particle centroid were converted to the coordinates parallel and perpendicular to the MT long axis, respectively.

The diameter of the particle under observation was estimated from its light intensity (see Fig. S2 and Methods in the Supporting Material). The minimum particle diameter detectable by our DFM was ∼40 nm, and only those particles with diameters in the range of 59 ± 5 nm were used for the analysis. Particles that collided with each other (i.e., the centers of particles were separated by a distance <100 nm) or that approached the end of the MT (located <100 nm from the MT end) were excluded from the analysis.

To derive the diffusion constant of the particle, D (= 〈Δx²〉/2Δt; see Fig. 2 D), the positional data for 40–170 particles on 20–40 MTs over a total period of 100 s were subjected to analysis. For the particles with high amine densities (≥0.59 nm⁻³), which had very long durations of interaction with the MTs, positional recording for a single particle was limited to a maximum period of 30 s. The data collected from >40 particles (23–40 MTs) over a total period of 600 s were combined to calculate the diffusion constant. Particles that showed no movement (SD < 30 nm), either because they were attached to the MTs or stuck to the bottom of the flow cell, were excluded from the analysis.

Effective number of charges on particles

The effective number of charges simultaneously interact with MTs, Q, can be obtained by the equation Q = αρv_d, where v_d is the volume of the part of the particle located within a Debye length (κ⁻¹ = 1.29 nm in a solution of ionic strength 55.9 mM) of the MT surface (Fig. 3 D), and α is the activity coefficient. The value of v_d for a particle with a diameter of 59 nm was calculated to be 86.4 nm³. Using pH titration, the pK_a of the particle suspension was determined to be 6.8. Thus, in our solution condition of pH 6.8 (α = 0.5), Q = ρ × 43.2. As described in Methods in the Supporting Material, the value of Q can have an error range of ±20% due to the uncertainty related to the estimation of particle diameter by DFM. However, this level of error does not alter the relative values of Q for this series of particles with varying amine densities.

In this calculation, the particles are assumed to be perfect spheres. We have no information about the shape of particles in solution. Even if we assume the ellipsoidicity of the particles to be 1.13, as was observed for the particles on a charged carbon film by electron microscopy, the value of Q may have an error range of only ±10%.

Results and Discussion

One-dimensional Brownian motion of charged nanoparticles along MT filaments

Although various positively-charged nanoparticles are commercially available, nanoparticles composed of polystyrene expose hydrophobic functional groups on the surface and participate in both electrostatic and hydrophobic interactions with MTs. To avoid this situation and to examine rigorously the effects of electrostatic interactions, we synthesized nanoparticles that have hydrophilic surfaces using inverse emulsion polymerization of acrylamide (25). Positive charges were introduced onto these particles by amination of their amide residues (26). Nanoparticles with various amine densities (ρ-range, 0.30–0.96 nm⁻³) were prepared by changing the duration of amination (Table 1). These positively-charged particles of heterogeneous size were fractionated by sucrose density gradient centrifugation, and a population of particles with an average diameter of 57 ± 13 nm (mean ± SD) was selected for experimental use (Fig. 1, A–C).

The interactions of these charged nanoparticles with the MTs were examined directly by DFM (Fig. 1, D and E). To avoid changing the surface properties of the particles, we used neither fluorescent dyes (to probe the particles) nor blocking proteins (to prevent nonspecific binding of the particles to the glass surface), and we carefully optimized the assay conditions so as not to perturb the interaction of particles with the microtubules (see Materials and Methods for details). The uncharged particles did not interact with the MTs, whereas the positively-charged particles bound to the MTs and some of these latter particles showed back-and-forth movements along the long axes of the MTs (Movie S1). The total number of particles bound to the MT increased with increasing amine density, whereas the fraction of moving particles with respect to the total bound population declined with increasing amine density (Fig. 2 A). In this and the subsequent analyses (see Figs. 2 and 3), so as to assess rigorously the effects of charge density while restricting the influence of size variation, we limited our analyses to those particles with a diameter close to 60 nm (Table 1).

To measure the back-and-forth movements of the nanoparticles, their tracks were traced on video at a rate of 30 frame/s, and the displacements achieved in the directions longitudinal and perpendicular to the MT long axes were analyzed (Fig. 2 B). Movement was essentially confined to the longitudinal axis of the MT. The SD for displacement for motion perpendicular to the MT long axis was ∼25 nm, which was equal to the background level of our measurement. The distributions of the net longitudinal displacements in 0.5-, 1.0-, and 2.0-s time intervals fitted well with the Gaussian distributions (Fig. 2 C). The mean-square displacement (MSD) of the distribution appeared to be a linear function of time (Fig. 2 D), indicating that the movement is due to thermally driven Brownian motion. Our results clearly demonstrate that nonspecific electrostatic interactions are sufficient to support the one-dimensional Brownian motion of nanoparticles along the MTs. The mean displacement, taking into account MT polarity, was essentially zero, indicating that the Brownian motion was not biased for any direction (Fig. 2 E).

The number of charges determines both the magnitude of diffusion and the duration of interaction

The number of charges affected not only the proportions of moving/stationary particles (Fig. 2 A), but also the magnitude of diffusion (Fig. 3 A, Movie S1). To quantify how an electrostatic interaction modulates the properties of diffusion, the diffusion constant and duration of interaction were measured for nanoparticles with different amine densities (Fig. 3, B and C).

From the amine density (ρ), particle diameter, and the Debye length in solution (κ⁻¹ = 1.29 nm), it is possible to calculate the number of effective charges on a particle that can interact with an MT (Q) (the charges in the yellow area shown in Fig. 3 D; see Materials and Methods for details of the calculation). Thus, in Fig. 3, B and C, τ_dur or D was plotted as a function of both ρ and Q.

For nanoparticles with amine density of 0.30 nm⁻³, both the speed and amplitude of the diffusional movement were very high, deriving the diffusion constant of 0.89 μm²/s (Fig. 3 B). With increasing amine density of the particle, the diffusion constant decreased. For nanoparticles with amine densities <0.30 nm⁻³, the duration of interaction was too short to allow measurement of the diffusion constant.

The observed relationship between D and Q shown in Fig. 3 B shows a good fit to the equation,

$$D/D_0=e^{-Q\Delta E_1/k_{\text{B}}T},$$ (1)

where k_B is the Boltzmann constant, and T is the temperature, deriving D₀ = 3.0 μm²/s and ΔE₁ = 0.10 k_BT per charge (equivalent to 0.06 kcal/mol of charge at 25°C; the reduced χ² of the fit was 1.4). The estimated size of D₀ is comparable to the unconstrained diffusion of a particle with a diameter of ∼59 nm (= 2a) in proximity to the MT surface, as predicted from Stokes' law (= k_BT/6πηa; 2.4–5.2 μm²/s). In proximity to the MT surface, the viscous drag on a particle is higher than that in solution, due to the wall effect (29) (for details of this calculation, see Methods in the Supporting Material). The implication of the energy QΔE₁ will be discussed in the following section.

The durations of interactions between the nanoparticles and MTs showed an exponential probability distribution (Fig. S3), and the exponential decay constant gave a measure of the mean duration τ_dur. For particles with amine densities in the range of 0.30–0.55 nm⁻³, τ_dur increased with increasing amine density (Fig. 3 C). For particles with amine densities >0.55 nm⁻³, the interaction lasted for several tens of seconds and measurement of τ_dur was practically impossible.

The observed dependence of τ_dur on Q (Fig. 3 C) is well represented by

$$\tau {}_0/{\tau }_{\text{dur}}=e^{-Q\Delta E_2/k_{\text{B}}T},$$ (2)

deriving two constants, τ₀ = 3.6 ms and ΔE₂ = 0.22 k_BT per charge (= 0.13 kcal/mol of charge). In both Eqs. 1 and 2, the Boltzmann constant is included in the exponential factor, on the assumption that some thermal activation-type process is involved in each reaction. The meaning of the energies QΔE₂ will be discussed in the following section.

A model: potential valley surrounding the MT

The inequality ΔE₂ > ΔE₁ indicates that the thermal activation of a particle in a radial direction (i.e., dissociation from MT) is distinct from the thermal activation of a particle along the MT (i.e., one-dimensional diffusion), although both are associated with charge-dependent interactions. One possible scenario is that a particle undergoes forth-and-back between the static, bound state (state B) and the activated, mobile state (state A) in the vicinity of the MT, until it is further activated to the free three-dimensional space (state F) (Fig. 4 A; modification of the model is possible and it will be discussed at the end of this section). The hypothesis can be formulated as

$$\mathrm{B}\underset{k_{-}}{\overset{k_{+}}{\rightleftharpoons }}\mathrm{A}\stackrel{k_{\text{off}}}{\rightleftharpoons }\mathrm{F},$$ (3)

where each energy QΔE₁ and QΔE₂ corresponds to the activation energy required for the transition from state B to A and from state B to F, respectively (Q-independent contributions are ignored).

Figure 4.

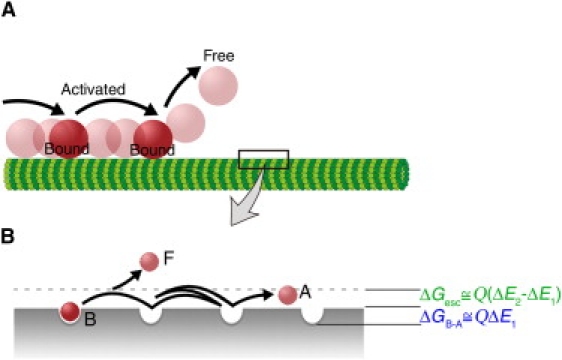
Three-state model for one-dimensional Brownian motion of charged nanoparticles along MTs. (A) Schematic diagram showing that one-dimensional Brownian motion comprises three states: the particle undergoes repeated cycles of binding to and movement along the MT until it finally dissociates from the MT. (B) The postulated distribution of potential energy along the MT.

The transitions between B and A states are essentially analogous in behavior to that of a counterion on a polyelectrolyte, whereby the counterion moves along the cylindrical potential valley that surrounds the linear polyelectrolyte, with intermittent pauses at potential holes on the polyelectrolyte (30,31).

In our experiment, this transition is very rapid, and each B and A state is too short to be resolved with the spatiotemporal resolution of our imaging system. Thus, we simply assume that states B and A are in equilibrium (this is analogous to the activated complex theory of Eyring (32) or to the Michaelis-Menten reaction scheme (33)). As the value D₀ in Eq. 1 was comparable to the unconstrained diffusion constant, we can assume that state A is a potential plateau (Fig. 4 B). In that case, the ratio D/D₀ corresponds to the fraction of time the particle stays in state A:

$$D/D_0=k_{+}/(k_{+}+k_{-})\text{.}$$ (4)

The fact that D/D₀ is only ∼10⁻¹–10⁻² in real data justifies the approximation k₊ /(k₊+k_–) ≈ k₊/k_–. By comparing Eqs. 1 and 4, we can identify the activation energy QΔE₁ with the standard free energy difference between states B and A, ΔG_B-A, in the ratio k₊/k_– as

$$D/D_0\cong k_{+}/k_{-}=e^{-\Delta G_{\text{B}-\text{A}}/k_{\text{B}}T}\cong e^{-Q\Delta E_1/k_{\text{B}}T}\text{.}$$ (5)

Quantitatively, D/D₀ takes the value of 0.271–0.015 (for a particle with Q in the range of 13–42). This means that, while the particle with the smallest number of charges (Q = 13) spent ∼20% of the time in state A, the particle with the largest number of charges (Q = 42) spent only 1.5% of the time in state A. These numbers will be compared with those of the protein molecules later.

Based on Eq. 5, we can identify the difference QΔE₂–QΔE₁ as the activation barrier from the potential plateau to the outer space (from state A to F; Fig. 4 B). Then, the dissociation rate of a particle from state A, k_off, can be described as a function of the activation free energy, ΔG_esc^‡,

$$k_{\text{off}}={\tau }_{00}^{-1}{e}^{-\Delta G_{\text{esc}}^{‡}/k_{\text{B}}T}\cong {\tau }_{00}^{-1}{e}^{-Q\left(\Delta E_2-\Delta E_1\right)/k_{\text{B}}T},$$ (6)

where τ₀₀⁻¹ is an attempting frequency. In our simple model, we approximated with τ₀₀ = τ₀ (see Appendix A for details).

It has to be noted that charged particles bind to and move along the MTs at the expense of purging monovalent or divalent cations condensed on the MTs (34–37). Thus, in terms of energy difference, QΔE₁ and QΔE₂–QΔE₁ should contain both electrostatic energy and Q-dependent entropy gain due to a counterion release. In this study, we simply analyze the influences of varying charges on the behavior of the particles without going into such detailed calculations.

The above model includes a type of hopping model in which the particle repeatedly hops between the potential holes with an activation energy of QΔE₁. In this case, the plateau is reduced to an activation energy barrier for the hopping. Alternatively, the above model can be generalized by assuming that the transition from state A to B is also an activated process. In that case, Eqs. 4–6 remain valid. Irrespective of the detailed assumptions of the model, the inequality QΔE₂ > QΔE₁ is essential for one-dimensional Brownian motion to happen and this supports the picture of an electrostatic environment around the MT, a so-called potential valley (1).

Origin of the potential valley

Although our model elucidates the physical aspects of particle behavior on an MT, it does not describe the molecular entity responsible for the potential valley (ΔG_esc^‡). There are two possible mechanisms by which MTs can generate this potential valley.

The first possibility is that, because the negative charges are distributed at a high density along the outer ridge of the protofilament (38), at a level higher than the critical value required for counterion condensation, negative charges form an equipotential electric field along the length of the MT (30,31). As a consequence, analogous to the behavior of counterions, a positively-charged particle that is constrained in this potential field can move freely along the MT long axis.

The second possibility is that the flexible C-terminal tail of tubulin, which contains many acidic amino acid residues, generates a potential field that spreads in the shape of a hemisphere, equivalent to the apparent volume occupied by the flexible C-terminal tail. As the tails of the α- and β-tubulin subunits are arranged at 4-nm intervals along the length of the MT, and as an extended tail reaches >4 nm, these hemispheres may overlap with one another, thereby forming a potential valley along the length of the MT. In such a situation, a positively-charged particle can bind electrostatically to one of these C-terminal tails, switching to another tail in quick succession, in a manner analogous to the motion of Tarzan swinging along jungle vines (14). Both of these mechanisms are plausible and the validities of these hypotheses need to be tested experimentally. The reported loss of protein diffusion after removal of the C-terminal tail of tubulin (4,5,14) does not necessarily support the latter hypothesis, because proteolytic removal of the C-terminal tail also decreases the linear charge density of the MT (15,39).

Irrespective of whether the underlying mechanism involves a linear track of high charge density or a row of flexible charged tails, once the origin of the potential valley is clarified, synthetic nanotubes or filaments that are surrounded by cylindrical potential valleys could be manufactured by chemically modulating the surface charges of nanotubes or filaments (e.g., carboxylated carbon nanotubes). In a bimolecular reaction, when a reactant is integrated into such a charged polymer, its counterpart ligand or partner molecule with an opposite charge can home-in to the target by scanning along the charged polymer via one-dimensional diffusion. The encounter probability for the two components is expected to be much higher than that achieved via three-dimensional diffusion in solution (40,41). Indeed, previous studies on DNA binding proteins and MT depolymerizing factor MCAK have demonstrated that these enzymes are more efficient at reaching the specific target via one-dimensional diffusional searching, as compared to a search conducted via three-dimensional diffusion (4,18,42). If we can mimic these biological systems using nanotubes or filaments, this type of nanoengineering technique may have broad utility, from pure physical chemistry to enzymology, in terms of accelerating reaction rates.

One-dimensional Brownian motion of protein molecules

The one-dimensional Brownian motions of various proteins have been reported to depend critically on electrostatic interactions (1,4,5,43,44). Therefore, these motions might be executed through a mechanism similar to that of the charged nanoparticle characterized in this study. However, we cannot discuss in quantitative terms the energetic aspects of protein interactions, because the types of data used in our calculation for the charged particles are scarcely available for proteins. The only exception to this is the single-headed kinesin, KIF1A, for which the Q dependencies of D and τ_dur have been measured in the presence of ATP (14).

KIF1A mutants with various numbers of lysines in the so-called K-loop were produced, and it was found that in the presence of ATP, the diffusion constants of these KIF1A constructs, D, are virtually unaffected by Q. If we interpret their result in the framework of our three-state model, the energy ΔG_B-A for KIF1A is estimated to be 6.5 k_BT (see Appendix B), independent of the charges. This value is larger than that measured for the charged particle (ΔG_B-A = 1.3–4.2 k_BT, depending on the charge density of the particle). When this ΔG_B-A is converted to the equilibrium constant between A and B states, the calculated value (k₊/k_- = 0.0016) indicates that KIF1A spends only 0.16% of the time in state A. The result indicates that the observed diffusional motion of KIF1A along the MT is predominantly governed by the interaction in state B, which owes to the complementary tertiary structures of the interfaces between KIF1A and MTs. On the other hand, the duration of interaction of these constructs with MTs, τ_dur, is an exponential function of the number of positive charges in the K-loop (= Q). If we interpret this result in the framework of our three-state model, for KIF1A, ΔG_esc^‡ is calculated to be 0.64 k_BT (= ΔE₂–ΔE₁) per charge. Once again, this value is significantly larger than that measured for the charged nanoparticles (0.12 k_BT per charge). Compared with the nanoparticles, the deeper potential valley for KIF1A could be due to the flexibility of the surface structure of the motor (45). In summary, the interaction of KIF1A with an MT appears to be more stable in both the B and A states, as compared to that of the charged particle (see Appendix B for details of the calculation).

The parameters k₊/k₋ and k_off calculated for nanoparticles and KIF1A are summarized in Table 2. Although both particles and KIF1A exhibit Brownian motion which lasts for a period of subseconds-to-seconds, moving for a distance of up to microns in length, their elementary processes are different. In the case of KIF1A, the protein remains mostly in state B (k₊/k₋ = 0.0016), and the cumulative time KIF1A spends in state A, τ_A = τ_dur k₊/(k₊+k_–), is only 10 ms at maximum (for KIF1A construct CK6 with the maximum number of lysines in the K-loop). Nevertheless, its small size allows for high speed diffusion (D₀ = 28 μm²/s), leading to a run length comparable to that of the particle. In contrast, with a nanoparticle, its B-A equilibrium is biased more toward state A (k₊/k₋ = 0.015–0.27) as compared to that of KIF1A. Because of its large size and high charge density, the diffusion of a particle is very stable; the cumulative time a particle spends in state A, τ_A, is one-to-two orders-of-magnitude longer than the τ_A of KIF1A.

Table 2.

The parameters k₊/k₋ and k_off calculated for nanoparticles and KIF1A

Charged nanoparticle						KIF1A
Q	k+/k–∗	koff (s−1)†	τdur (ms)‡	τA (ms)§	Diffusion length (nm)¶	No. of lysine in K-loop	k+/k–‖	koff (s−1)∗∗	τdur (ms)††	τA (ms)‡‡	Diffusion length (nm) ¶
13	0.273	58.4	63	17.1	227	1	0.0015	3333	200	0.3	93
15	0.223	45.9	98	21.8	256	2	0.0015	1481	450	0.7	140
24	0.091	15.6	707	64.1	439	4	0.0015	635	1050	1.6	214
26	0.074	12.3	1098	81.5	495	6	0.0015	95	7000	10.5	553
32	0.041	6.0	4109	167.5	709
42	0.015	1.8	37084	556.1	1292

^∗$k_{+}/k_{-}\cong e^{-Q\Delta E_1/k_{\text{B}}T}$, where ΔE₁ = 0.1 k_BT.

^†$k_{\text{off}}\cong {\tau }_{00}^{-1}{e}^{-Q\left(\Delta E_2-\Delta E_1\right)/k_{\text{B}}T}$, where ΔE₂–ΔE₁ = 0.12 k_BT and τ₀₀ = 3.6 ms.

^‡${\tau }_{\mathrm{dur}}^{-1}={\tau }_{00}^{-1}{e}^{-Q\Delta E_2/k_{B}T}$, where ΔE₂ = 0.22 k_BT, τ₀₀ = 3.6 ms.

^§τ_A = k_off⁻¹.

^¶Diffusion length was estimated as ${\left(D_0{\tau }_{\text{A}}\right)}^{1/2}$, where D₀ = 3 μm²/s and 28 μm²/s for nanoparticle and KIF1A, respectively.

^‖$k_{+}/k_{-}\cong e^{-\Delta E_1/k_{\text{B}}T}$, where ΔE₁ = 6.5 k_BT. See Appendix B for detail.

^∗∗k_off = τ_A⁻¹.

^††Numbers taken from Fig. 3B in Okada and Hirokawa (14).

^‡‡${\tau }_{\text{A}}={\tau }_{\text{dur}}{e}^{-6.5}$.

KIF1A is the only example of the energetic aspects of protein Brownian motion analyzed to date in our three-state model. For DNA binding proteins, the duration of one-dimensional Brownian motion along DNA strands, τ_dur, is critically dependent upon the concentration of salt in the solution (46,47), which implicates a mechanism similar to that observed for MT-binding proteins (45). In future studies, if D and τ_dur are measured as a function of Q for these and other proteins that show one-dimensional Brownian motion, our model could provide a useful framework for analyses of the elementary processes involved in these motions. In particular, for motor proteins, the present approach will expedite the elucidation of the mechanism underlying the weak binding interaction.

Appendix A: Validation of the Approximation for τ₀₀

If we write the energies ΔG_B-A and ΔG_esc^‡ including the Q-independent terms as ΔG_B-A = QΔE₁+ΔG_B-A|_Q=0 and ΔG_esc^‡ = Q(ΔE₂–ΔE₁) + ΔG_esc^‡|_Q=0, respectively, we obtain τ₀⁻¹ = τ_dur⁻¹|_Q=0 = τ₀₀⁻¹ exp(–[ΔG_B-A|_Q=0 + ΔG_esc^‡|_Q=0]/k_BT). In our simple model (Eq. 6), we approximated τ₀₀ = τ₀ by neglecting the Q-independent contribution to ΔG_B-A and ΔG_esc^‡. However, this approximation may be too rough because: 1), τ₀₀ is usually much smaller than ms (32); and 2), the characteristic spatial scale obtained by the dimensional analysis using D₀ and τ₀, (D₀τ₀)^1/2 ≈ 104 (nm), is unusually large, and is much larger than the structural periodicity of MTs (tubulin dimer ≈ 8 nm). Therefore, the approximation for τ₀⁻¹ could be improved if it is replaced by the more precise relationship, τ₀⁻¹ = τ₀₀⁻¹exp(–ΔG_esc^‡|_Q=0/k_BT). In that case, the large ΔG_esc^‡|_Q=0 might be attributed to entropic dispersion effects (48–50).

Appendix B: Calculation of ΔG_b-A and ΔG_esc^‡ for Kif1a

According to the data shown in Fig. 3 E of Okada and Hirokawa (14), D of KIF1A was 0.044 μm²/s, independent of the number of charges (Q). As the diffusion constant of a protein with a diameter of 5 nm, D₀, is expected to be 28 μm²/s (= k_BT/6πηa; Stokes' law) near the MT surface (see Methods in the Supporting Material for details of the calculation), the ΔG_B-A for KIF1A is estimated to be ∼6.5 k_BT (= –ln(D/D₀)), whereby its Q-dependent term is sufficiently small to be ignored (ΔE₁ ≈ 0). In contrast, the data presented in Fig. 3B of Okada and Hirokawa (14) show that the duration of interaction τ_dur is an exponential function of the charges, with the exponent being 0.64 k_BT (= ΔE₂) per charge. Consequently, the ΔG_esc^‡ for KIF1A is calculated to be 0.64 k_BT (= ΔE₂–ΔE₁) per charge. The cumulated time the particle spends in state A, τ_A, was led from τ_dur by the relationship τ_A = τ_dure^−6.5 (Table 2).

Supporting Material

Supporting methods, one table, three figures, and one movie are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00095-0.