High Order Total Variation Minimization for Interior Tomography

Abstract

Recently, an accurate solution to the interior problem was proposed based on the total variation (TV) minimization, assuming that a region of interest (ROI) is piecewise constant. In this paper, we generalize that assumption to allow a piecewise polynomial ROI, introduce the high order TV (HOT), and prove that an ROI can be accurately reconstructed from projection data associated with x-rays through the ROI through the HOT minimization if the ROI is piecewise polynomial. Then, we verify our theoretical results in numerical simulation.

I. Introduction

While classic CT theory targets exact reconstruction of a whole cross-section or an entire object from un-truncated projections, practical applications often focus on much smaller regions of interest (ROIs). Classic CT theory cannot exactly reconstruct an internal ROI only from truncated projections associated with x-rays through the ROI because this interior problem does not have a unique solution [1-2]. When applying traditional CT algorithms for interior reconstruction from truncated projection data, features outside the ROI may seriously disturb inside features and often hide diagnostic information.

Over past decades, lambda tomography has been extensively studied [3-5][6-10] but it only targets gradient-like features and has not been well received in the biomedical community. In recent work, Ye et al. found that the interior problem can be exactly and stably solved if a sub-region in the ROI is known [11]. Similar results were also independently reported by other researchers [12-13]. However, it can be difficult to obtain precise prior knowledge of a sub-region in many cases such as cardiac CT perfusion studies.

The classic Nyquist sampling theorem states that one must sample a signal at least twice faster than its bandwidth to keep all the information. Surprisingly, an emerging theory – compressive sensing (CS) – promises to capture compressible signals at a much lower rate than the Nyquist rate and yet allows accurate reconstruction of such a signal from a limited number of samples [14-15]. The main idea of CS is that most signals are sparse in appropriate orthonormal systems, that is, a majority of their coefficients are close or equal to zero. Typically, CS starts with taking a limited amount of representative measures, and then recovers a signal with an overwhelming probability via the ${\ell }_1$ norm minimization. Since the number of samples is limited, recovery of the signal or image would involve solving an underdetermined matrix equation. That is, there are many candidate solutions that can all well fit the incomplete measurement. Thus, some additional constraint is needed to select the “best” candidate. While the classic solution is to minimize the ${\ell }_2$ norm, Donoho, Candes, Romberg and Tao showed that finding the candidate with the minimum ${\ell }_1$ norm, which leads to the TV minimization in some cases, is most likely the correct choice [14-15].

Under the guidance of CS theory, we recently demonstrated that exact interior reconstruction could be achieved if an ROI is piecewise constant [16-19]. Inspired by these results, here we extend their work to utilize more general prior knowledge for interior tomography. Specifically, we will prove that if an ROI is piecewise polynomial, then the interior problem can be accurately solved through the high order TV (HOT) minimization.

The organization of this paper is as follows. In the next section, the interior problem will be defined. In the third section, our theoretical findings will be presented. In the fourth section, numerical results will be described to support our methodology. In the last section, related issues will be discussed.

II. Interior Problem

Without loss of generality, we assume the following conditions throughout this paper:

• Condition (1) An object image f₀(x) is compactly supported on a disc ${\Omega }_A=\{x=(x_1,x_2)\in {\mathbb{R}}^2:\mid x\mid <A\}$, where A is a positive constant. Furthermore, f₀(x) is a piecewise smooth function; that is, Ω_A can be partitioned into finitely many sub-domains ${\left\{D_j\right\}}_{j=1}^{N_0}$, such that f₀(x) is smooth with bounded derivatives in each D_j;

• Condition (2) An internal ROI is a smaller disc ${\Omega }_a=\{x=(x_1,x_2)\in {\mathbb{R}}^2:\mid x\mid <a\}$, as shown in Fig. 1, where a is a positive constant and a < A;

• Condition (3) Projections through the ROI

  $$R{f}_0(s,\theta )={\int }_{-\infty }^{\infty }{f}_0(s\theta +t{\theta }^{\perp })dt,-a<s<a,\theta \in S^1,$$ (1)

  are available, where θ = (cos φ, sin φ), θ^⊥ = (−sin φ, cos φ), 0 ≤ φ < 2π.

Figure 1.

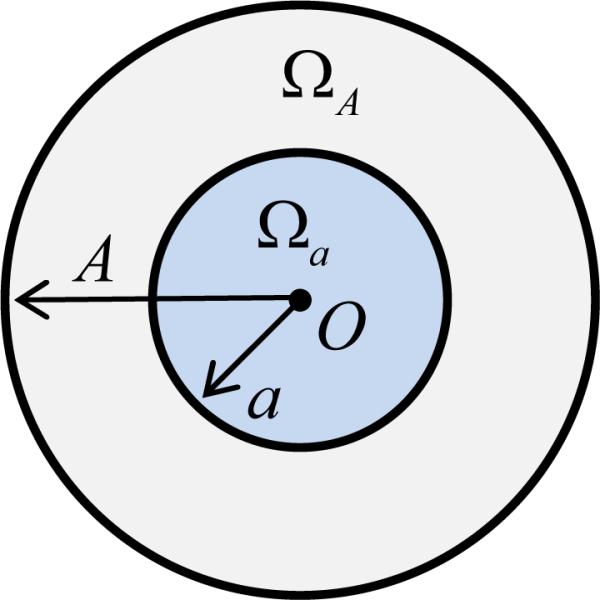
Region of interest (ROI) inside a compact support.

The interior problem is to find an image f(x) such that

• Condition (4) f(x) is a piecewise smooth function and compactly supported on the disc Ω_A;

• Condition (5) Rf(s,θ) = Rf₀(s,θ), −a < s < a, θ ∈ S¹.

It is well known that under the conditions (4) and (5) the interior problem does not have a unique solution [1-2]. The following theorem characterizes the structure of solutions to the interior problem.

Theorem 1. Any image f(x) satisfying Conditions (4) and (5) can be written as f(x) = f₀(x) + u(x) for $x\in {\mathbb{R}}^2$, where u(x) is an analytic function in the disc Ω_a, and

$$Ru(s,\theta )=0,-a<s<a,\theta \in S^1.$$

We call such an image f(x) a candidate image, and correspondingly u(x) an ambiguity image.

Proof: Let u(x) = f(x)–f₀(x). Clearly, u(x) is a piecewise smooth function and compactly supported on the disc Ω_A, and

$$Ru(s,\theta )=0,-a<s<a,\theta \in S^1.$$ (2)

By the well-known Radon inversion formula, we have

$$u\left(x\right)=\frac{1}{4{\pi }^2}{\int }_0^{2\pi }{\int }_{\mid s\mid \ge a}\frac{{\partial }_{s}Ru(\theta ,s)}{x•\theta -s}dsd\phi ,x\in {\Omega }_a.$$ (3)

By the Taylor expansion

$$\frac{1}{x•\theta -s}=-\frac{1}{s(1-x•\theta ∕s)}=-\sum _{k=0}^{\infty }\frac{{\left(x•\theta \right)}^k}{s^{k+1}},$$ (4)

we obtain

$$u\left(x\right)=\sum _{k=0}^{\infty }\sum _{k_1+k_2=k}{c}_{k_1,k_2}{x}_1^{k_1}{x}_2^{k_2}.$$ (5)

Hence, the function u(x) is an analytic function in Ω_a. Examples of non-zero ambiguity images can be found in [1].

From now on, let u(x) always represent an ambiguity image unless otherwise stated. Theorem 1 suggests that the interior problem can be solved by utilizing appropriate a priori knowledge. In the following, we will introduce the concept of the high order TV (HOT) and minimize it to solve the interior problem exactly under the assumption that an image f₀(x) is a piecewise polynomial function in an ROI Ω_a.

III. Theoretical Analysis

If an object image f₀(x) is a piecewise polynomial function in an ROI Ω_a, we can prove that f₀(x) is the only candidate image that minimizes the HOT to be defined by Eqs. (44-45) and (81-82). First, let us prove that if an ambiguity image is a polynomial function in Ω_a, then it must be zero. This result will be formally stated as Theorem 2. In order to prove Theorem 2, we will need Lemmas 1 and 2.

Lemma 1. Suppose that a is a positive constant. If

• (a) g(z) is an analytic function in $\mathbb{C}\backslash (-\infty ,-a]\cup [a,+\infty )$;

• (b) p(x) is a polynomial function;

• (c) $g\left(x\right)=\frac{1}{\pi }\mathrm{p}.\mathrm{v}{\int }_{\mid t\mid <a}\frac{p\left(t\right)}{x-t}dt$, for x ∈ (−a,a),

then $\underset{y\to 0+}{\lim }\mathrm{Im}\left(g(x+iy)\right)=p\left(x\right)$, for $x\in (-\infty ,-a)\cup (a,+\infty )$.

Proof: Since g(z) is uniquely determined by its value on interval (−a,a) and

$$g\left(x\right)=\frac{1}{\pi }\mathrm{p}.\mathrm{v}{\int }_{\mid t\mid <a}\frac{p\left(t\right)}{x-t}dt,\text{for}x\in (-a,a),$$ (6)

g(z) is uniquely determined by p(x) for x ∈ (−a,a). Let g(z) be denoted by g_n(z) with respect to p(x) = xⁿ. Because of the linear relationship between g(z) and p(x), it suffices to prove the lemma in the case p(x) = xⁿ (n = 0, 1, 2,···). That is, we need to prove

$$\underset{y\to 0+}{\text{lim}}\mathrm{Im}\left(g_n(x+iy)\right)=x^n,\text{for}x\in (-\infty ,-a)\cup (a,+\infty ),n=0,1,2,\cdots .$$ (7)

Let us proceed by induction with respect to n . When n = 0 , that is, p(x) = 1, we have

$$g_0\left(x\right)=\frac{1}{\pi }\mathrm{p}.\mathrm{v}{\int }_{\mid t\mid <a}\frac{1}{x-t}dt=\frac{1}{\pi }(\ln (a+x)-\ln (a-x)),\text{for}x\in (-a,a).$$ (8)

Hence,

$$g_0\left(z\right)=\frac{1}{\pi }(\ln (a+z)-\ln (a-z)),\text{for}z\in \mathbb{C}\backslash (-\infty ,-a]\cup [a,+\infty ),$$ (9)

where the principal value interval for the logarithm function is (−π,π). That is,

$$\ln (a+z)=\ln \mid a+z\mid +i\text{arg}(a+z),-\pi <\text{arg}(a+z)<\pi ,\text{for}z\in \mathbb{C}\backslash (-\infty ,-a],$$ (10)

and

$$\ln (a-z)=\ln \mid a-z\mid +i\text{arg}(a-z),-\pi <\text{arg}(a-z)<\pi ,\text{for}z\in \mathbb{C}\backslash [a,+\infty ).$$ (11)

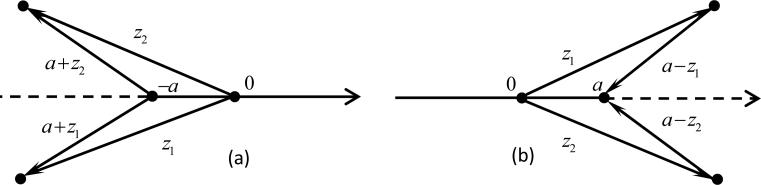
As shown in Fig. 2, arg(a − z₁) approaches −π when arg(a + z₁) is close to −π, and arg(a − z₂) approaches π when arg(a + z₂) is close to π. Clearly,

$$\mathrm{Im}\left(g_0\left(z\right)\right)=\frac{1}{\pi }(\text{arg}(a+z)-\text{arg}(a-z)),\text{for}z\in \mathbb{C}\backslash (-\infty ,-a]\cup [a,+\infty ).$$ (12)

Since

$$\underset{y\to 0+}{\text{lim}}\text{arg}(a+x+iy)=\pi ,\underset{y\to 0+}{\text{lim}}\text{arg}(a-x-iy)=0,\text{for}x\in (-\infty ,-a)$$ (13)

and

$$\underset{y\to 0+}{\text{lim}}\text{arg}(a+x+iy)=0,\underset{y\to 0+}{\text{lim}}\text{arg}(a-x-iy)=-\pi ,\text{for}x\in (a,\infty ),$$ (14)

we have

$$\underset{y\to 0+}{\text{lim}}\mathrm{Im}\left(g_0(x+iy)\right)=1,\text{for}x\in (-\infty ,-a)\cup (a,+\infty ).$$ (15)

For n > 0 and x ∈(−a,a), we have

$$g_n\left(x\right)=\frac{1}{\pi }\mathrm{p}.\mathrm{v}{\int }_{\mid t\mid <a}\frac{t^n}{x-t}dt=\frac{1}{\pi }\mathrm{p}.\mathrm{v}{\int }_{\mid t\mid <a}\frac{(t^n-x{t}^{n-1})+x{t}^{n-1}}{x-t}dt=-\frac{1}{\pi }{\int }_{\mid t\mid <a}{t}^{n-1}dt+\frac{x}{\pi }\mathrm{p}.\mathrm{v}{\int }_{\mid t\mid <a}\frac{t^{n-1}}{x-t}dt=-\frac{1}{n\pi }(a^n-{(-a)}^n)+x{g}_{n-1}\left(x\right).$$ (16)

Therefore,

$$g_n\left(z\right)=-\frac{1}{n\pi }(a^n-{(-a)}^n)+z{g}_{n-1}\left(z\right),\text{for}z\in \mathbb{C}\backslash (-\infty ,-a]\cup [a,+\infty ),$$ (17)

and

$$\mathrm{Im}\left(g_n\left(z\right)\right)=\mathrm{Im}\left(z{g}_{n-1}\left(z\right)\right),\text{for}z\in \mathbb{C}\backslash (-\infty ,-a]\cup [a,+\infty ).$$ (18)

For $x\in (-\infty ,-a)\cup (a,+\infty )$ and y > 0 , we have

$$\mathrm{Im}\left(g_n(x+iy)\right)=x\mathrm{Im}\left(g_{n-1}(x+iy)\right)+y\mathrm{Re}\left(g_{n-1}(x+iy)\right),$$ (19)

and

$$\underset{y\to 0+}{\text{lim}}\mathrm{Im}\left(g_n(x+iy)\right)=x\underset{y\to 0+}{\text{lim}}\mathrm{Im}\left(g_{n-1}(x+iy)\right)=x^2\underset{y\to 0+}{\text{lim}}\mathrm{Im}\left(g_{n-2}(x+iy)\right)=\cdots =x^n\underset{y\to 0+}{\text{lim}}\mathrm{Im}\left(g_0(x+iy)\right)=x^n,$$ (20)

which completes the proof of Lemma 1.

Figure 2.

Illustration of (a) arg(a+z) and (b) arg(a-z).

Lemma 2. Suppose that a and A are positive constants with a < A. If a function v(x) satisfies

• (d) v(x) is bounded with supp v ⊆ [−A,A];

• (e) v(x) = p(x) for x ∈ (−a,a), where p(x) is a polynomial function;

• (f) Hv(x) = 0, for x ∈ (−a,a), where Hv(x) is the Hilbert transform of v(x), that is,

  $$Hv\left(x\right)=\frac{1}{\pi }\mathrm{p}.\mathrm{v}.{\int }_{\mathbb{R}}\frac{v\left(t\right)}{x-t}dt,$$

  then v(x) = 0, for x ∈ (−∞,∞).

Proof: The function (see Corollary 4.1.2 on page 40 in [20])

$$g\left(z\right)=\frac{1}{\pi }{\int }_{\mid t\mid \ge a}\frac{v\left(t\right)}{t-z}dt,$$ (21)

is analytic on $\mathbb{C}\backslash (-\infty ,-a]\cup [a,+\infty )$. Since

$$\frac{1}{t-(x+iy)}=\frac{t-x+iy}{{(t-x)}^2+y^2},$$ (22)

we have

$$\mathrm{Im}\left(g(x+iy)\right)=\frac{1}{\pi }{\int }_{\mid t\mid \ge a}\frac{y}{{(t-x)}^2+y^2}v\left(t\right)dt=\frac{1}{\pi }{\int }_{\mathbb{R}}\frac{y}{{(t-x)}^2+y^2}\tilde{v}\left(t\right)dt=\frac{1}{\pi }{\int }_{\mathbb{R}}\frac{1}{{\left(\frac{t-x}{y}\right)}^2+1}\tilde{v}\left(t\right)d\left(\frac{t-x}{y}\right)=\frac{1}{\pi }{\int }_{\mathbb{R}}\frac{1}{{\tau }^2+1}\tilde{v}(x+\tau y)d\tau ,\text{for}y>0,$$ (23)

where

$$\tilde{v}\left(x\right)=\{\begin{array}{c}v\left(x\right),x\in (-\infty ,-a)\cup (a,\infty )\hfill \\ 0,x\in [-a,a]\hfill \end{array}\phantom{\}}.$$ (24)

Because ṽ(x) can be written as

$$\tilde{v}\left(x\right)=\frac{1}{\pi }{\int }_{\mathbb{R}}\frac{1}{{\tau }^2+1}\tilde{v}\left(x\right)d\tau ,$$ (25)

we have

$$\underset{y\to 0+}{\text{lim}}{\int }_{\mathbb{R}}\mid \mathrm{Im}\left(g(x+iy)\right)-\tilde{v}\left(x\right)\mid dx\le \underset{y\to 0+}{\text{lim}}\left\{\frac{1}{\pi }{\int }_{\mathbb{R}}\frac{{\Vert \tilde{v}(•+\tau y)-\tilde{v}\left(•\right)\Vert }_1}{{\tau }^2+1}d\tau \right\}=0,$$ (26)

where

$${\Vert \tilde{v}(•+\tau y)-\tilde{v}\left(•\right)\Vert }_1={\int }_{\mathbb{R}}\mid \tilde{v}(x+\tau y)-\tilde{v}\left(x\right)\mid dx.$$ (27)

Therefore,

$$\underset{y\to 0+}{\text{lim}}\mathrm{Im}\left(g(x+iy)\right)=\tilde{v}\left(x\right)=v\left(x\right),$$ (28)

for $x\in (-\infty ,-a)\cup (a,\infty )$ almost everywhere (a.e.).

By Condition (f), we have

$$g\left(x\right)=\frac{1}{\pi }\mathrm{p}.\mathrm{v}{\int }_{\mathbb{R}}\frac{v\left(t\right)}{t-x}dt-\frac{1}{\pi }\mathrm{p}.\mathrm{v}{\int }_{\mid t\mid <a}\frac{v\left(t\right)}{t-x}dt=Hv\left(x\right)+\frac{1}{\pi }\mathrm{p}.\mathrm{v}{\int }_{\mid t\mid <a}\frac{p\left(t\right)}{x-t}dt=\frac{1}{\pi }\mathrm{p}.\mathrm{v}{\int }_{\mid t\mid <a}\frac{p\left(t\right)}{x-t}dt,\text{for}x\in (-a,a).$$ (29)

By Lemma 1, we obtain

$$\underset{y\to 0+}{\text{lim}}\mathrm{Im}\left(g(x+iy)\right)=p\left(x\right),\text{for}x\in (-\infty ,-a)\cup (a,+\infty ).$$ (30)

Combining Eq. (28), (30) and Condition (e), we have

$$v\left(x\right)=p\left(x\right),\text{for}\mathrm{a}.\mathrm{e}.x\in (-\infty ,\infty ).$$ (31)

Condition (d) and Eq. (31) imply p(x) ≡ 0. Hence, v(x) = 0, for a.e. x ∈ (−∞,∞), which completes the proof.

Theorem 2. If an ambiguity image u(x) satisfies

• (g) u(x) = p(x) for x ∈Ω_a, where p(x) is a 2-D polynomial function;

• (h) Ru(s,θ) = 0, for s ∈ (−a,a), θ ∈ S¹,

then u(x) = 0.

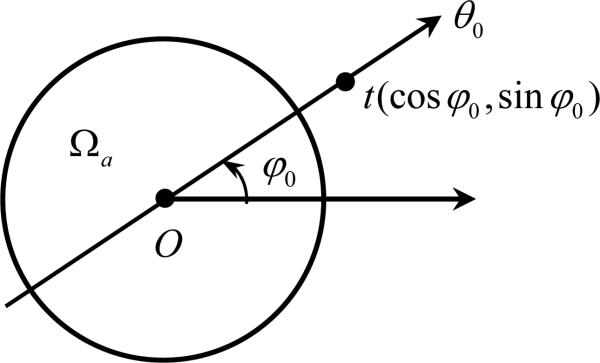
Proof: As illustrated in Fig. 3, for an arbitrary φ₀ ∈[0,π), let L_θ0 denote the line through the origin and tilted by θ₀ = (cos φ₀, sin φ₀). When u(x) is restricted to the line L_θ0, it can be expressed as

$$v_{{\theta }_0}\left(t\right)=u\left(t(\text{cos}{\phi }_0,\text{sin}{\phi }_0)\right),t\in (-\infty ,\infty ).$$ (32)

By the relationship between the differentiated backprojection of projection data and the Hilbert transform of an image [21-22], we have

$$H{v}_{{\theta }_0}\left(t\right)=-\frac{1}{2\pi }{\int }_{{\phi }_0-\frac{\pi }{2}}^{{\phi }_0+\frac{\pi }{2}}\frac{\partial Ru(s,\theta )}{\partial s}{\mid }_{s=x_{{\theta }_0}^t\cdot \theta }d\phi ,$$ (33)

where $x_{{\theta }_0}^t=t(\cos {\phi }_0,\sin {\phi }_0)$, θ = (cos φ, sin φ).

Figure 3.

Radial line through the origin.

By Condition (g) and Eq. (32), we have

$$v_{{\theta }_0}\left(t\right)=p\left(t(\text{cos}{\phi }_0,\text{sin}{\phi }_0)\right),\text{for}t\in (-a,a),$$ (34)

where p(t(cos φ₀, sin φ₀)) is a polynomial function with respect to t. By Condition (h) and Eq. (33), we have

$$H{v}_{{\theta }_0}\left(t\right)=0,\text{for}t\in (-a,a).$$ (35)

By Lemma 2, we obtain that v_θ0t = 0, which implies that u(x) = 0.

Now, let us analyze a candidate image under the assumption that f₀(x) is a piecewise polynomial function in Ω_a.

Theorem 3. Suppose that an object image f₀(x) is a piecewise polynomial function in Ω_a. If a candidate image f(x) is also a piecewise polynomial function in Ω_a, then f(x) = f₀(x).

Proof: By Theorem 1, we have that f(x) = f₀(x) + u(x), where u(x) is an analytic function in Ω_a. On the other hand, by the assumption of Theorem 3, u(x) = f(x) − f₀(x) is also a piecewise polynomial function in Ω_a. Combining these two facts, u(x) must be a polynomial function in Ω_a. Then, by Theorem 2 we have u(x) = 0.

Theorem 3 suggests that f₀(x) can be singled out among all candidate images by minimizing some kind of high order TV. For simplicity, let us first assume that an object image f₀(x) is a piecewise linear function in Ω_a; that is, Ω_a can be decomposed into finitely many sub-domains: ${\left\{{\Omega }_i\right\}}_{i=1}^m$ (Fig. 4) such that

$$f_0\left(x\right)=f_i\left(x\right)=a_i{x}_1+b_i{x}_2+c_i,\text{for}x\in {\Omega }_i,1\le i\le m,$$ (36)

and each sub-domain Ω_i is adjacent to its neighboring sub-domains Ω_j with piecewise smooth boundaries Γ_i,j,, j ∈ N_i.

Figure 4.

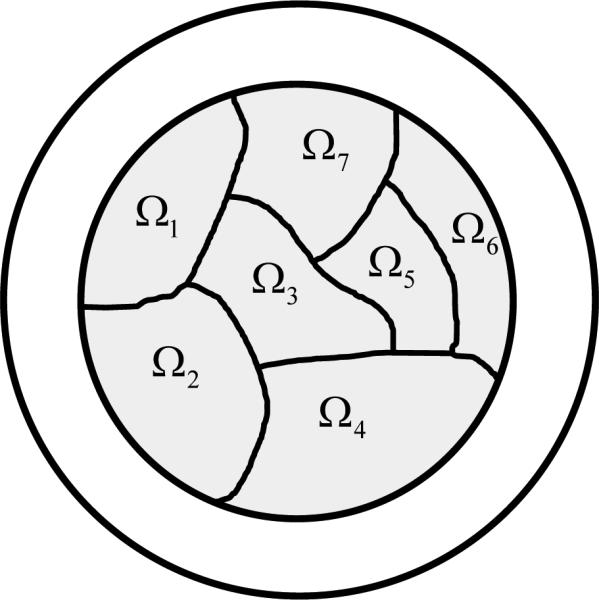
ROI consisting of 7 sub-domains.

If m = 1, that is, f₀(x) is a linear function in Ω_a, then any candidate image f(x) = f₀(x) + u(x) is a smooth function in Ω_a. We define the second order TV for any candidate image f(x) of this type as

$${\mathrm{HOT}}_2\left(f\right)={\int }_{{\Omega }_a}\text{min}\left(\underset{\theta \in S^1}{\text{max}}\mid \frac{df}{d\theta }\left(x\right)\mid ,\underset{\theta \in S^1}{\text{max}}\mid \frac{d^{2}f}{d{\theta }^2}\left(x\right)\mid \right)d{x}_{1}d{x}_2.$$ (37)

where θ = (cos φ, sin φ), φ ∈ [0, 2 π), $\frac{df}{d\theta }\left(x\right)={\frac{d{f}_{x,\theta }\left(t\right)}{dt}\mid }_{t=0}$, $\frac{d^{2}f}{d{\theta }^2}\left(x\right)={\frac{d^2{f}_{x,\theta }\left(t\right)}{d{t}^2}\mid }_{t=0}$ and f_x,θ(t) = f(x + tθ), t ∈ (−(ε,ε).

Note that if $\frac{\partial f}{\partial x_1}$, $\frac{\partial f}{\partial x_2}$ are continuous at x, then

$$\frac{df}{d\theta }\left(x\right)=\frac{\partial f}{\partial x_1}\left(x\right)\text{cos}\phi +\frac{\partial f}{\partial x_2}\left(x\right)\text{sin}\phi .\text{for}\theta =(\text{cos}\phi ,\text{sin}\phi )\in S^1.$$ (38)

Hence,

$$\underset{\theta \in S^1}{\text{max}}\mid \frac{df}{d\theta }\left(x\right)\mid =\sqrt{{\left(\frac{\partial f}{\partial x_1}\left(x\right)\right)}^2+{\left(\frac{\partial f}{\partial x_2}\left(x\right)\right)}^2}.$$ (39)

There also exists a similar formula for $\underset{\theta \in S^1}{\max }\mid \frac{d^{2}f}{d{\theta }^2}\left(x\right)\mid$, as represented in the following Lemma.

Lemma 3. Suppose that f(x) is a candidate image. If $\frac{{\partial }^{2}f}{\partial {x_1}^2}$, $\frac{{\partial }^{2}f}{\partial x_1\partial x_2}$ and $\frac{{\partial }^{2}f}{\partial {x_2}^2}$ are continuous at x, then

$$\underset{\theta \in S^1}{\text{max}}\mid \frac{d^{2}f}{d{\theta }^2}\left(x\right)\mid =\sqrt{\frac{1}{4}{\left(\frac{{\partial }^{2}f}{\partial {x_1}^2}\left(x\right)-\frac{{\partial }^{2}f}{\partial {x_2}^2}\left(x\right)\right)}^2+{\left(\frac{{\partial }^{2}f}{\partial x_1\partial x_2}\left(x\right)\right)}^2}+\frac{1}{2}\mid \frac{{\partial }^{2}f}{\partial {x_1}^2}\left(x\right)+\frac{{\partial }^{2}f}{\partial {x_2}^2}\left(x\right)\mid .$$ (40)

Proof: If $\frac{{\partial }^{2}f}{\partial {x_1}^2}$, $\frac{{\partial }^{2}f}{\partial x_1\partial x_2}$ and $\frac{{\partial }^{2}f}{\partial {x_2}^2}$ are continuous at x, then

$$\begin{array}{cc}\hfill & \frac{d^{2}f}{d{\theta }^2}\left(x\right)={\left(\frac{\partial }{\partial x_1}\text{cos}\phi +\frac{\partial }{\partial x_2}\text{sin}\phi \right)}^{2}f\left(x\right)\hfill \\ \hfill & =\frac{{\partial }^{2}f}{\partial {x_1}^2}\left(x\right){\text{cos}}^2\phi +2\frac{{\partial }^{2}f}{\partial x_1\partial x_2}\left(x\right)\text{cos}\phi \text{sin}\phi +\frac{{\partial }^{2}f}{\partial {x_2}^2}\left(x\right){\text{sin}}^2\phi \hfill \\ \hfill & =\frac{{\partial }^{2}f}{\partial {x_1}^2}\left(x\right)\left(\frac{1+\text{cos}2\phi }{2}\right)+\frac{{\partial }^{2}f}{\partial x_1\partial x_2}\left(x\right)\text{sin}2\phi +\frac{{\partial }^{2}f}{\partial {x_2}^2}\left(x\right)\left(\frac{1-\text{cos}2\phi }{2}\right)\hfill \\ \hfill & =\frac{1}{2}\left(\frac{{\partial }^{2}f}{\partial {x_1}^2}\left(x\right)+\frac{{\partial }^{2}f}{\partial {x_2}^2}\left(x\right)\right)+\frac{1}{2}\left(\frac{{\partial }^{2}f}{\partial {x_1}^2}\left(x\right)-\frac{{\partial }^{2}f}{\partial {x_2}^2}\left(x\right)\right)\text{cos}2\phi +\frac{{\partial }^{2}f}{\partial x_1\partial x_2}\left(x\right)\text{sin}2\phi .\hfill \end{array}$$ (41)

Thus, $\mid \frac{d^{2}f}{d{\theta }^2}\left(x\right)\mid$ reaches its maximum when

$$(\text{cos}2\phi ,\text{sin}2\phi )=\frac{\text{sgn}\left(\frac{1}{2}\left(\frac{{\partial }^{2}f}{\partial {x_1}^2}\left(x\right)+\frac{{\partial }^{2}f}{\partial {x_2}^2}\left(x\right)\right)\right)\left(\frac{1}{2}\left(\frac{{\partial }^{2}f}{\partial {x_1}^2}\left(x\right)-\frac{{\partial }^{2}f}{\partial {x_2}^2}\left(x\right)\right),\frac{{\partial }^{2}f}{\partial x_1\partial x_2}\left(x\right)\right)}{\sqrt{\frac{1}{4}{\left(\frac{{\partial }^{2}f}{\partial {x_1}^2}\left(x\right)-\frac{{\partial }^{2}f}{\partial {x_2}^2}\left(x\right)\right)}^2}+{\left(\frac{{\partial }^{2}f}{\partial x_1\partial x_2}\left(x\right)\right)}^2}.$$ (42)

This leads to Eq. (40).

Combining Eqs. (37), (39) and (40), we have

$${\mathrm{HOT}}_2\left(f\right)={\int }_{{\Omega }_a}\text{min}\left\{\sqrt{\frac{1}{4}{\left(\frac{{\partial }^{2}f}{\partial {x_1}^2}-\frac{{\partial }^{2}f}{\partial {x_2}^2}\right)}^2+{\left(\frac{{\partial }^{2}f}{\partial x_1\partial x_2}\right)}^2}+\frac{1}{2}\mid \frac{{\partial }^{2}f}{\partial {x_1}^2}+\frac{{\partial }^{2}f}{\partial {x_2}^2}\mid ,\sqrt{{\left(\frac{\partial f}{\partial x_1}\right)}^2+{\left(\frac{\partial f}{\partial x_2}\right)}^2}\right\}d{x}_{1}d{x}_2.$$ (43)

where f(x) = f₀(x) + u(x), and f₀(x) is a linear function in Ω_a.

If m > 1, $\frac{df}{d\theta }\left(x\right)$ or $\frac{d^{2}f}{d{\theta }^2}\left(x\right)$ may not exist on the boundaries $\bigcup _{i=1}^m\bigcup _{j>i,j\in N_i}{\Gamma }_{i,j}$ Hence, we need modify the definition Eq. (37) of the second order TV to incorporate jumps of the image f(x) at Γ_i,j into the second order TV. To address the discontinuity of the first and second order derivatives across internal boundaries, we define the second order TV as the limit of the following sum:

$${\mathrm{HOT}}_2\left(f\right)=\underset{\left(\underset{1\le k\le M}{\text{max}}diam\left\{Q_k\right\}\right)\to 0}{\text{lim sup}}\sum _{k=1}^M{I}_k\left(f\right),$$ (44)

where ${\left\{Q_k\right\}}_{k=1}^M$ is an arbitrary partition of Ω_a, diam(Q_k) the diameter of Q_k, and

$$I_k\left(f\right)=\text{min}\left(\underset{\theta \in S^1}{\text{sup}}\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{\int }_{Q_k}f\left(x\right)\frac{dg}{d\theta }\left(x\right)dx,\underset{\theta \in S^1}{\text{sup}}\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{\int }_{Q_k}f\left(x\right)\frac{d^{2}g}{d{\theta }^2}\left(x\right)dx\right).$$ (45)

In the following Lemma, we will derive an explicit formula for HOT₂(f ).

Lemma 4. Suppose that an object image f₀(x) is a piecewise linear function in Ω_a as defined by Eq. (36). For any candidate image f(x) = f₀(x) + u(x), we have

$${\mathrm{HOT}}_2\left(f\right)=\sum _{i=1}^m\sum _{j>i,j\in N_i}{\int }_{{\Gamma }_{i,j}}\mid (a_i-a_j)x_1+(b_i-b_j)x_2+(c_i-c_j)\mid ds+{\int }_{{\Omega }_a}\text{min}\left\{\sqrt{\frac{1}{4}{\left(\frac{{\partial }^{2}f}{\partial {x_1}^2}-\frac{{\partial }^{2}f}{\partial {x_2}^2}\right)}^2+{\left(\frac{{\partial }^{2}f}{\partial x_1\partial x_2}\right)}^2}+\frac{1}{2}\mid \frac{{\partial }^{2}f}{\partial {x_1}^2}+\frac{{\partial }^{2}f}{\partial {x_2}^2}\mid ,\sqrt{{\left(\frac{\partial f}{\partial x_1}\right)}^2+{\left(\frac{\partial f}{\partial x_2}\right)}^2}\right\}d{x}_{1}d{x}_2,$$ (46)

where the second term is a Lebesgue integral.

Proof: Note that f(x) = f₀(x) + u(x), where u(x) is an analytic function. Let ${\left\{Q_k\right\}}_{k=1}^M$ be an arbitrary partition of Ω_a. First, let us consider Q_k which covers a common boundary Γ_i,j of a pair of neighboring sub-domains Ω_i and Ω_j, and is contained in ${\Omega }_i\cup {\Omega }_j$ (Fig. 5 (a)). Let θ_N be the normal vector of the curve Γ_i,j pointing from Ω_j towards Ω_i, and <θ,θ_N > the angle between the vectors θ and θ_N. For $g\in C_0^{\infty }\left(Q_k\right)$, we have

$${\int }_{Q_k}f\left(x\right)\frac{dg}{d\theta }\left(x\right)dx={\int }_{Q_k\cap {\Omega }_i}f\left(x\right)\frac{dg}{d\theta }\left(x\right)dx+{\int }_{Q_k\cap {\Omega }_j}f\left(x\right)\frac{dg}{d\theta }\left(x\right)dx.$$ (47)

Performing 2-D integration by parts on the two terms of the right-hand side of Eq. (47) respectively, and utilizing the fact that g(x) = 0 near the boundary of Q_k, we have

$${\int }_{Q_k\cap {\Omega }_i}f\left(x\right)\frac{dg}{d\theta }\left(x\right)dx>-{\int }_{{\Gamma }_{i,j}\cap Q_k}(f_i\left(x\right)+u\left(x\right))g\left(x\right)\text{cos}<\theta ,{\theta }_N>ds-{\int }_{Q_k\cap {\Omega }_i}\frac{df}{d\theta }\left(x\right)g\left(x\right)dx,$$ (48)

$${\int }_{Q_k\cap {\Omega }_j}f\left(x\right)\frac{dg}{d\theta }\left(x\right)dx={\int }_{{\Gamma }_{i,j}\cap Q_k}(f_j\left(x\right)+u\left(x\right))g\left(x\right)\text{cos}<\theta ,{\theta }_N>ds-{\int }_{Q_k\cap {\Omega }_j}\frac{df}{d\theta }\left(x\right)g\left(x\right)dx.$$ (49)

Inserting Eqs. (48) and (49) into Eq. (47), we obtain

$${\int }_{Q_k}f\left(x\right)\frac{dg}{d\theta }\left(x\right)dx={\int }_{{\Gamma }_{i,j}\cap Q_k}(f_j\left(x\right)-f_i\left(x\right))g\left(x\right)\text{cos}<\theta ,{\theta }_N>ds-{\int }_{Q_k\cap {\Omega }_i}\frac{df}{d\theta }\left(x\right)g\left(x\right)dx-{\int }_{Q_k\cap {\Omega }_j}\frac{df}{d\theta }\left(x\right)g\left(x\right)dx.$$ (50)

We have

$$\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{\int }_{{\Gamma }_{i,j}\cap Q_k}(f_j\left(x\right)-f_i\left(x\right))g\left(x\right)\text{cos}<\theta ,{\theta }_N>ds={\int }_{{\Gamma }_{i,j}\cap Q_k}\mid (f_j\left(x\right)-f_i\left(x\right))\text{cos}<\theta ,{\theta }_N>\mid ds,$$ (51)

$$\underset{\theta \in S^1}{\text{sup}}\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{\int }_{{\Gamma }_{i,j}\cap Q_k}(f_j\left(x\right)-f_i\left(x\right))g\left(x\right)\text{cos}<\theta ,{\theta }_N>ds={\int }_{{\Gamma }_{i,j}\cap Q_k}\mid f_j\left(x\right)-f_i\left(x\right)\mid ds+o\left(1\right)\mid {\Gamma }_{i,j}\cap Q_k\mid .$$ (52)

where o(1) represents an infinitesimal, satisfying $\underset{\left(\underset{1\le k\le M}{\max }diam\left\{Q_k\right\}\right)\to 0}{\lim }o\left(1\right)=0$. Besides, we have

$${\int }_{Q_k\cap {\Omega }_i}\frac{df}{d\theta }\left(x\right)g\left(x\right)dx=O\left(1\right)\mid Q_k\cap {\Omega }_i\mid ,$$ (53)

$${\int }_{Q_k\cap {\Omega }_i}\frac{df}{d\theta }\left(x\right)g\left(x\right)dx=O\left(1\right)\mid Q_k\cap {\Omega }_i\mid ,$$ (54)

where O(1) represents a quantity bounded by a constant which does not depend on Q_k. Summing Eqs. (53-54) up, we obtain

$${\int }_{Q_k\cap {\Omega }_i}\frac{df}{d\theta }\left(x\right)g\left(x\right)dx+{\int }_{Q_k\cap {\Omega }_i}\frac{df}{d\theta }\left(x\right)g\left(x\right)dx=O\left(1\right)\mid Q_k\mid .$$ (55)

Combining Eqs. (50), (52) and (55), we obtain

$$\underset{\theta \in S^1}{\text{sup}}\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{\int }_{Q_k}f\left(x\right)\frac{dg}{d\theta }\left(x\right)dx={\int }_{{\Gamma }_{i,j}\cap Q_k}\mid f_j\left(x\right)-f_i\left(x\right)\mid ds+O\left(1\right)\mid Q_k\mid +o\left(1\right)\mid {\Gamma }_{i,j}\cap Q_k\mid .$$ (56)

Repeatedly performing 2-D integration by parts, for $g\in C_0^{\infty }\left(Q_k\right)$, we have

$$\begin{array}{cc}\hfill & {\int }_{Q_k}f\left(x\right)\frac{d^{2}g}{d{\theta }^2}\left(x\right)dx={\int }_{Q_k\cap {\Omega }_i}f\left(x\right)\frac{d^{2}g}{d{\theta }^2}\left(x\right)dx+{\int }_{Q_k\cap {\Omega }_j}f\left(x\right)\frac{d^{2}g}{d{\theta }^2}\left(x\right)dx\hfill \\ \hfill & ={\int }_{{\Gamma }_{i,j}\cap Q_k}(f_j\left(x\right)-f_i\left(x\right))\frac{dg}{d\theta }\left(x\right)\text{cos}<\theta ,{\theta }_N>ds-{\int }_{Q_k\cap {\Omega }_i}\frac{df}{d\theta }\left(x\right)\frac{dg}{d\theta }\left(x\right)dx-{\int }_{Q_k\cap {\Omega }_j}\frac{df}{d\theta }\left(x\right)\frac{dg}{d\theta }\left(x\right)dx\hfill \\ \hfill & ={\int }_{{\Gamma }_{i,j}\cap Q_k}(f_j\left(x\right)-f_i\left(x\right))\frac{dg}{d\theta }\left(x\right)\text{cos}<\theta ,{\theta }_N>ds-{\int }_{{\Gamma }_{i,j}\cap Q_k}(\frac{d{f}_j}{d\theta }\left(x\right)-\frac{d{f}_i}{d\theta }\left(x\right))g\left(x\right)\text{cos}<\theta ,{\theta }_N>ds+{\int }_{Q_k\cap {\Omega }_i}\frac{d^{2}f}{d^2\theta }\left(x\right)g\left(x\right)dx+{\int }_{Q_k\cap {\Omega }_j}\frac{d^{2}f}{d{\theta }^2}\left(x\right)g\left(x\right)dx\hfill \\ \hfill & ={\int }_{{\Gamma }_{i,j}\cap Q_k}(f_j\left(x\right)-f_i\left(x\right))\frac{dg}{d\theta }\left(x\right)\text{cos}<\theta ,{\theta }_N>ds-{\int }_{{\Gamma }_{i,j}\cap Q_k}(\frac{d{f}_j}{d\theta }\left(x\right)-\frac{d{f}_i}{d\theta }\left(x\right))g\left(x\right)\text{cos}<\theta ,{\theta }_N>ds+{\int }_{Q_k}\frac{d^{2}f}{d{\theta }^2}\left(x\right)g\left(x\right)dx.\hfill \end{array}$$ (57)

For the second term on the right-hand side of Eq. (57), we have

$$\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{\int }_{{\Gamma }_{i,j}\cap Q_k}(\frac{d{f}_j}{d\theta }\left(x\right)-\frac{d{f}_i}{d\theta }\left(x\right))g\left(x\right)\text{cos}<\theta ,{\theta }_N>ds={\int }_{{\Gamma }_{i,j}\cap Q_k}\mid \frac{d{f}_j}{d\theta }\left(x\right)-\frac{d{f}_i}{d\theta }\left(x\right)\mid \text{cos}<\theta ,{\theta }_N>ds,$$ (58)

$$\underset{\theta \in S^1}{\text{sup}}\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{\int }_{{\Gamma }_{i,j}\cap Q_k}(\frac{d{f}_j}{d\theta }\left(x\right)-\frac{d{f}_i}{d\theta }\left(x\right))g\left(x\right)\text{cos}<\theta ,{\theta }_N>ds={\int }_{{\Gamma }_{i,j}\cap Q_k}\underset{\theta \in S^1}{\text{max}}\left(\mid \frac{d{f}_j}{d\theta }\left(x\right)-\frac{d{f}_i}{d\theta }\left(x\right)\mid \text{cos}<\theta ,{\theta }_N>\right)ds+o\left(1\right)\mid {\Gamma }_{i,j}\cap Q_k\mid .$$ (59)

For the third term on the right-hand side of Eq. (57), we have

$${\int }_{Q_k}\frac{d^{2}f}{d{\theta }^2}\left(x\right)g\left(x\right)dx=O\left(1\right)\mid Q_k\mid .$$ (60)

Next, let us evaluate $\underset{\theta \in S^1}{\sup }\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\sup }{\int }_{Q_k}f\left(x\right)\frac{d^{2}g}{d{\theta }^2}\left(x\right)dx$ in the following two cases.

Figure 5.

Sub-domain Q_k of (a) the first and (b) second types.

Case 1: If there exists some $x\in {\Gamma }_{i,j}\cap Q_k$ such that f_j(x) − f_i(x) ≠ 0, then for θ ∈ S¹, an arbitrary real constant C and an arbitrary compact set $K\subset Q_k$, there exists a $g\in C_0^{\infty }\left(Q_k\right)$ satisfying |g(x|≤1 and

$$\frac{dg}{d\theta }\left(x\right)=C(f_j\left(x\right)-f_i\left(x\right)),\text{for}x\in {\Gamma }_{i,j}\cap K,\text{and}$$ (61)

we have

$$\underset{\theta \in S^1}{\text{sup}}\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{\int }_{{\Gamma }_{i,j}\cap Q_k}(f_j\left(x\right)-f_i\left(x\right))\frac{dg}{d\theta }\left(x\right)\text{cos}<\theta ,{\theta }_N>ds=+\infty .$$ (62)

Combining Eqs. (59), (60) and (62), we obtain

$$\underset{\theta \in S^1}{\text{sup}}\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{\int }_{Q_k}f\left(x\right)\frac{d^{2}g}{d{\theta }^2}\left(x\right)dx\ge \underset{\theta \in S^1}{\text{sup}}\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{\int }_{{\Gamma }_{i,j}\cap Q_k}(f_j\left(x\right)-f_i\left(x\right))\frac{dg}{d\theta }\left(x\right)\text{cos}<\theta ,{\theta }_N>ds-\underset{\theta \in S^1}{\text{sup}}\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{\int }_{{\Gamma }_{i,j}\cap Q_k}(\frac{d{f}_j}{d\theta }\left(x\right)-\frac{d{f}_i}{d\theta }\left(x\right))g\left(x\right)\text{cos}<\theta ,{\theta }_N>ds-\underset{\theta \in S^1}{\text{sup}}\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{\int }_{Q_k}\frac{d^{2}f}{d{\theta }^2}\left(x\right)g\left(x\right)dx=+\infty .$$ (63)

Case 2: Otherwise, f_j(x) − f_i(x) = 0 for any $x\in {\Gamma }_{i,j}\cap Q_k$, and the first term on the right-hand side of Eq. (57) equals 0. Then, we have

$$\underset{\theta \in S^1}{\text{sup}}\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{\int }_{Q_k}f\left(x\right)\frac{d^{2}g}{d{\theta }^2}\left(x\right)dx={\int }_{{\Gamma }_{i,j}\cap Q_k}\underset{\theta \in S^1}{\text{max}}\left(\mid \frac{d{f}_j}{d\theta }\left(x\right)-\frac{d{f}_i}{d\theta }\left(x\right)\mid \text{cos}<\theta ,{\theta }_N>\right)ds+O\left(1\right)\mid Q_k\mid +o\left(1\right)\mid {\Gamma }_{i,j}\cap Q_k\mid .$$ (64)

In this case, we also have

$${\int }_{{\Gamma }_{i,j}\cap Q_k}\mid f_j\left(x\right)-f_i\left(x\right)\mid ds=0,$$ (65)

$$\begin{array}{cc}\hfill & \underset{\theta \in S^1}{\text{sup}}\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{\int }_{Q_k}f\left(x\right)\frac{dg}{d\theta }\left(x\right)dx\hfill \\ \hfill & ={\int }_{{\Gamma }_{i,j}\cap Q_k}\mid f_j\left(x\right)-f_i\left(x\right)\mid ds+O\left(1\right)\mid Q_k\mid +o\left(1\right)\mid {\Gamma }_{i,j}\cap Q_k\mid \hfill \\ \hfill & =O\left(1\right)\mid Q_k\mid +o\left(1\right)\mid {\Gamma }_{i,j}\cap Q_k\mid .\hfill \end{array}$$ (66)

Combining Eqs. (63), (64) and (66), we arrive at the following conclusion: If Q_k covers the common boundary Γ_i,j of a pair of neighboring sub-domains Ω_i and Ω_j and is contained in ${\Omega }_i\cup {\Omega }_j$, then

$$\begin{array}{cc}\hfill & I_k\left(f\right)=\text{min}\left(\underset{\theta \in S^1}{\text{sup}}\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{\int }_{Q_k}f\left(x\right)\frac{dg}{d\theta }\left(x\right)dx,\underset{\theta \in S^1}{\text{sup}}\underset{\theta \in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{\int }_{Q_k}f\left(x\right)\frac{d^{2}g}{d{\theta }^2}\left(x\right)dx\right)\hfill \\ \hfill & =\underset{\theta \in S^1}{\text{sup}}\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{\int }_{Q_k}f\left(x\right)\frac{dg}{d\theta }\left(x\right)dx\hfill \\ \hfill & ={\int }_{{\Gamma }_{i,j}\cap Q_k}\mid f_j\left(x\right)-f_i\left(x\right)\mid ds+O\left(1\right)\mid Q_k\mid +o\left(1\right)\mid {\Gamma }_{i,j}\cap Q_k\mid \hfill \\ \hfill & ={\int }_{{\Gamma }_{i,j}\cap Q_k}\mid (a_i-a_j)x_1+(b_i-b_j)x_2+(c_i-c_j)\mid ds+O\left(1\right)\mid Q_k\mid +o\left(1\right)\mid {\Gamma }_{i,j}\cap Q_k\mid .\hfill \end{array}$$ (67)

Next, let us consider Q_k that is completely contained in some sub-domain Ω_i (Fig. 5(b)). For $g\in C_0^{\infty }\left(Q_k\right)$, performing 2-D integration by parts again we have

$${\int }_{Q_k}f\left(x\right)\frac{dg}{d\theta }\left(x\right)dx=-{\int }_{Q_k}\frac{df}{d\theta }\left(x\right)g\left(x\right)dx,$$ (68)

$${\int }_{Q_k}f\left(x\right)\frac{d^{2}g}{d{\theta }^2}\left(x\right)dx={\int }_{Q_k}\frac{d^{2}f}{d{\theta }^2}\left(x\right)g\left(x\right)dx.$$ (69)

Hence,

$$\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{\int }_{Q_k}f\left(x\right)\frac{dg}{d\theta }\left(x\right)dx={\int }_{Q_k}\mid \frac{df}{d\theta }\left(x\right)\mid dx,$$ (70)

$$\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{\int }_{Q_k}f\left(x\right)\frac{d^{2}g}{d{\theta }^2}\left(x\right)dx={\int }_{Q_k}\mid \frac{d^{2}f}{d{\theta }^2}\left(x\right)\mid dx.$$ (71)

Furthermore,

$$\underset{\theta \in S^1}{\text{sup}}\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{\int }_{Q_k}f\left(x\right)\frac{dg}{d\theta }\left(x\right)dx={\int }_{Q_k}\underset{\theta \in S^1}{\text{max}}\mid \frac{df}{d\theta }\left(x\right)\mid dx+o\left(1\right)\mid Q_k\mid ,$$ (72)

$$\underset{\theta \in S^1}{\text{sup}}\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{\int }_{Q_k}f\left(x\right)\frac{d^{2}g}{d{\theta }^2}\left(x\right)dx={\int }_{Q_k}\underset{\theta \in S^1}{\text{max}}\mid \frac{d^{2}f}{d{\theta }^2}\left(x\right)\mid dx+o\left(1\right)\mid Q_k\mid .$$ (73)

Combining Eqs. (72-73), we have

$$\begin{array}{cc}\hfill & I_k\left(f\right)=\text{min}\left(\underset{\theta \in S^1}{\text{sup}}\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{\int }_{Q_k}f\left(x\right)\frac{dg}{d\theta }\left(x\right)dx,\underset{\theta \in S^1}{\text{sup}}\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{\int }_{Q_k}f\left(x\right)\frac{d^{2}g}{d{\theta }^2}\left(x\right)dx\right)\hfill \\ \hfill & ={\int }_{Q_k}\text{min}\left(\underset{\theta \in S^1}{\text{max}}\frac{df}{d\theta }\left(x\right)dx,\underset{\theta \in S^1}{\text{max}}\frac{d^{2}f}{d{\theta }^2}\left(x\right)\right)dx+o\left(1\right)\mid Q_k\mid \hfill \\ \hfill & ={\int }_{Q_k}\text{min}\left\{\sqrt{\frac{1}{4}{\left(\frac{{\partial }^{2}f}{\partial {x_1}^2}-\frac{{\partial }^{2}f}{\partial {x_2}^2}\right)}^2+{\left(\frac{{\partial }^{2}f}{\partial x_1\partial x_2}\right)}^2}+\frac{1}{2}\mid \frac{{\partial }^{2}f}{\partial {x_1}^2}+\frac{{\partial }^{2}f}{\partial {x_2}^2}\mid ,\sqrt{{\left(\frac{\partial f}{\partial x_1}\right)}^2+{\left(\frac{\partial f}{\partial x_2}\right)}^2}\right\}d{x}_{1}d{x}_2+o\left(1\right)\mid Q_k\mid ,\hfill \end{array}$$ (74)

where we have used the fact that f₀(x) is a piecewise linear function, $\frac{{\partial }^{2}f}{\partial {x_1}^2}$, $\frac{{\partial }^{2}f}{\partial x_1\partial x_2}$ and $\frac{{\partial }^{2}f}{\partial {x_2}^2}$ are continuous at $x\in {\Omega }_a\backslash \bigcup _{i=1}^m\bigcup _{j>1,j\in N_i}{\Gamma }_{i,j}$. Combining (67) and (74), we obtain

$$\sum _{k=1}^M{I}_k\left(f\right)=\sum _{i=1}^m\sum _{j>i,j\in N_i}{\int }_{{\Gamma }_{i,j}}\mid (a_i-a_j)x_1+(b_i-b_j)x_2+(c_i-c_j)\mid ds+{\int }_{{\Omega }_a}\text{min}\left\{\sqrt{\frac{1}{4}{\left(\frac{{\partial }^{2}f}{\partial {x_1}^2}-\frac{{\partial }^{2}f}{\partial {x_2}^2}\right)}^2+{\left(\frac{{\partial }^{2}f}{\partial x_1\partial x_2}\right)}^2}+\frac{1}{2}\mid \frac{{\partial }^{2}f}{\partial {x_1}^2}+\frac{{\partial }^{2}f}{\partial {x_2}^2}\mid ,\sqrt{{\left(\frac{\partial f}{\partial x_1}\right)}^2+{\left(\frac{\partial f}{\partial x_2}\right)}^2}\right\}d{x}_{1}d{x}_2+O\left(1\right)\left(\sum _{i=1}^m\sum _{j>i,j\in N_i}\mid {\Gamma }_{i,j}\mid \right)\left(\underset{1\le k\le M}{\text{max}}diam\left\{Q_k\right\}\right)+o\left(1\right)\mid {\Omega }_a\mid .$$ (75)

Therefore, we have

$$\begin{array}{cc}\hfill & {\mathrm{HOT}}_2\left(f\right)=\underset{\left(\underset{1\le k\le M}{\text{max}}diam\left\{Q_k\right\}\right)\to 0}{\text{lim sup}}\sum _{k=1}^M{I}_k\left(f\right)\hfill \\ \hfill & =\sum _{i=1}^m\sum _{j>i,j\in N_i}{\int }_{{\Gamma }_{i,j}}\mid (a_i-a_j)x_1+(b_i-b_j)x_2+(c_i-c_j)\mid ds+{\int }_{{\Omega }_a}\text{min}\left\{\sqrt{\frac{1}{4}{\left(\frac{{\partial }^{2}f}{\partial {x_1}^2}-\frac{{\partial }^{2}f}{\partial {x_2}^2}\right)}^2+{\left(\frac{{\partial }^{2}f}{\partial x_1\partial x_2}\right)}^2}+\frac{1}{2}\mid \frac{{\partial }^{2}f}{\partial {x_1}^2}+\frac{{\partial }^{2}f}{\partial {x_2}^2}\mid ,\sqrt{{\left(\frac{\partial f}{\partial x_1}\right)}^2+{\left(\frac{\partial f}{\partial x_2}\right)}^2}\right\}d{x}_{1}d{x}_2.\hfill \end{array}$$ (76)

which completes the proof of Lemma 4.

For the second term of Eq. (46), because of the zero Lebesgue measure of $\bigcup _{i=1}^m\bigcup _{j>i,j\in N_i}{\Gamma }_{i,j}$, even if

$$\text{min}\left\{\sqrt{\frac{1}{4}{\left(\frac{{\partial }^{2}f}{\partial {x_1}^2}\left(x\right)-\frac{{\partial }^{2}f}{\partial {x_2}^2}\left(x\right)\right)}^2+{\left(\frac{{\partial }^{2}f}{\partial x_1\partial x_2}\left(x\right)\right)}^2}+\frac{1}{2}\mid \frac{{\partial }^{2}f}{\partial {x_1}^2}\left(x\right)+\frac{{\partial }^{2}f}{\partial {x_2}^2}\left(x\right)\mid ,\sqrt{{\left(\frac{\partial f}{\partial x_1}\left(x\right)\right)}^2+{\left(\frac{\partial f}{\partial x_2}\left(x\right)\right)}^2}\right\}$$ (77)

does not exist for $x\in \bigcup _{i=1}^m\bigcup _{j>i,j\in N_i}{\Gamma }_{i,j}$, the value of

$${\int }_{{\Omega }_a}\text{min}\left\{\sqrt{\frac{1}{4}{\left(\frac{{\partial }^{2}f}{\partial {x_1}^2}-\frac{{\partial }^{2}f}{\partial {x_2}^2}\right)}^2+{\left(\frac{{\partial }^{2}f}{\partial x_1\partial x_2}\right)}^2}+\frac{1}{2}\mid \frac{{\partial }^{2}f}{\partial {x_1}^2}+\frac{{\partial }^{2}f}{\partial {x_2}^2}\mid ,\sqrt{{\left(\frac{\partial f}{\partial x_1}\right)}^2+{\left(\frac{\partial f}{\partial x_2}\right)}^2}\right\}d{x}_{1}d{x}_2$$ (78)

will remain well defined in the sense of Lebesgue integral.

Now, our main contribution can be presented in the following Theorem.

Theorem 4. Suppose that an object image f₀(x) is a piecewise linear function in Ω_a as defined by Eq. (36). If h(x) is a candidate image and ${\mathrm{HOT}}_2\left(h\right)=\underset{f=f_0+u_1}{\min }{\mathrm{HOT}}_2\left(f\right)$ where u₁(x) is an arbitrary ambiguity image, then h(x) = f₀(x) for x ∈Ω_a.

Proof: Let h(x) = f₀(x) + u(x) for some ambiguity image u . By Lemma 4, we have

$${\mathrm{HOT}}_2\left(f\right)\ge \sum _{i=1}^m\sum _{j>i,j\in N_i}{\int }_{{\Gamma }_{i,j}}\mid (a_i-a_j)x_1+(b_i-b_j)x_2+(c_i-c_j)\mid ds,\text{for}f\left(x\right)=f_0\left(x\right)+u_1\left(x\right),$$ (79)

where u₁(x) is an arbitrary ambiguity image, and

$${\mathrm{HOT}}_2\left(f_0\right)=\sum _{i=1}^m\sum _{j>i,j\in N_i}{\int }_{{\Gamma }_{i,j}}\mid (a_i-a_j)x_1+(b_i-b_j)x_2+(c_i-c_j)\mid ds.$$ (80)

Hence,

$$\underset{f=f_0+u_1}{\text{min}}{\mathrm{HOT}}_2\left(f\right)=\sum _{i=1}^m\sum _{j>i,j\in N_i}{\int }_{{\Gamma }_{i,j}}\mid (a_i-a_j)x_1+(b_i-b_j)x_2+(c_i-c_j)\mid ds.$$ (81)

Because ${\mathrm{HOT}}_2\left(h\right)=\underset{f=f_0+u}{\min }{\mathrm{HOT}}_2\left(f\right)$, we have

$${\int }_{{\Omega }_a}\text{min}\left\{\sqrt{\frac{1}{4}{\left(\frac{{\partial }^{2}h}{\partial {x_1}^2}-\frac{{\partial }^{2}h}{\partial {x_2}^2}\right)}^2+{\left(\frac{{\partial }^{2}h}{\partial x_1\partial x_2}\right)}^2}+\frac{1}{2}\mid \frac{{\partial }^{2}h}{\partial {x_1}^2}+\frac{{\partial }^{2}h}{\partial {x_2}^2}\mid ,\sqrt{{\left(\frac{\partial h}{\partial x_1}\right)}^2+{\left(\frac{\partial h}{\partial x_2}\right)}^2}\right\}d{x}_{1}d{x}_2=0.$$ (82)

Therefore,

$$\text{min}\left\{\sqrt{\frac{1}{4}{\left(\frac{{\partial }^{2}h}{\partial {x_1}^2}\left(x\right)-\frac{{\partial }^{2}h}{\partial {x_2}^2}\left(x\right)\right)}^2+{\left(\frac{{\partial }^{2}h}{\partial x_1\partial x_2}\left(x\right)\right)}^2}+\frac{1}{2}\mid \frac{{\partial }^{2}h}{\partial {x_1}^2}\left(x\right)+\frac{{\partial }^{2}h}{\partial {x_2}^2}\left(x\right)\mid ,\sqrt{{\left(\frac{\partial h}{\partial x_1}\left(x\right)\right)}^2+{\left(\frac{\partial h}{\partial x_2}\left(x\right)\right)}^2}\right\}=0,\text{for}x\in {\Omega }_a\backslash \bigcup _{i=1}^m\bigcup _{j>i,j\in N_i}{\Gamma }_{i,j};$$ (83)

that is,

$$\sqrt{\frac{1}{4}{\left(\frac{{\partial }^{2}h}{\partial {x_1}^2}\left(x\right)-\frac{{\partial }^{2}h}{\partial {x_2}^2}\left(x\right)\right)}^2+{\left(\frac{{\partial }^{2}h}{\partial x_1\partial x_2}\left(x\right)\right)}^2}+\frac{1}{2}\mid \frac{{\partial }^{2}h}{\partial {x_1}^2}\left(x\right)+\frac{{\partial }^{2}h}{\partial {x_2}^2}\left(x\right)\mid =0\text{or}\sqrt{{\left(\frac{\partial h}{\partial x_1}\left(x\right)\right)}^2+{\left(\frac{\partial h}{\partial x_2}\left(x\right)\right)}^2}=0,\text{for}x\in {\Omega }_a\backslash \bigcup _{i=1}^m\bigcup _{j>i,j\in N_i}{\Gamma }_{i,j}.$$ (84)

We assert that

$$\sqrt{\frac{1}{4}{\left(\frac{{\partial }^{2}h}{\partial {x_1}^2}\left(x\right)-\frac{{\partial }^{2}h}{\partial {x_2}^2}\left(x\right)\right)}^2+{\left(\frac{{\partial }^{2}h}{\partial x_1\partial x_2}\left(x\right)\right)}^2}+\frac{1}{2}\mid \frac{{\partial }^{2}h}{\partial {x_1}^2}\left(x\right)+\frac{{\partial }^{2}h}{\partial {x_2}^2}\left(x\right)\mid =0,\text{for}x=(x_1,x_2)\in {\Omega }_a\backslash \bigcup _{i=1}^m\bigcup _{j>i,j\in N_i}{\Gamma }_{i,j}.$$ (85)

Otherwise, there exists some $x_0\in {\Omega }_a\backslash \bigcup _{i=1}^m\bigcup _{j>i,j\in N_i}{\Gamma }_{i,j}$ such that

$$\left(\sqrt{\frac{1}{4}{\left(\frac{{\partial }^{2}h}{\partial {x_1}^2}-\frac{{\partial }^{2}h}{\partial {x_2}^2}\right)}^2+{\left(\frac{{\partial }^{2}h}{\partial x_1\partial x_2}\right)}^2}+\frac{1}{2}\mid \frac{{\partial }^{2}h}{\partial {x_1}^2}+\frac{{\partial }^{2}h}{\partial {x_2}^2}\mid \right){\mid }_{x=x_0}>0,$$ (86)

By continuity, there exists a neighborhood of x₀ denoted by Ω_x0 such that

$${\Omega }_{x_0}\subset {\Omega }_a\backslash \bigcup _{i=1}^m\bigcup _{j>i,j\in N_i}{\Gamma }_{i,j},$$ (87)

and

$$\sqrt{\frac{1}{4}{\left(\frac{{\partial }^{2}h}{\partial {x_1}^2}\left(x\right)-\frac{{\partial }^{2}h}{\partial {x_2}^2}\left(x\right)\right)}^2+{\left(\frac{{\partial }^{2}h}{\partial x_1\partial x_2}\left(x\right)\right)}^2}+\frac{1}{2}\mid \frac{{\partial }^{2}h}{\partial {x_1}^2}\left(x\right)+\frac{{\partial }^{2}h}{\partial {x_2}^2}\left(x\right)\mid >0,\text{for}x\in {\Omega }_{x_0}.$$ (88)

By Eq. (84), we have

$$\sqrt{{\left(\frac{\partial h}{\partial x_1}\left(x\right)\right)}^2+{\left(\frac{\partial h}{\partial x_2}\left(x\right)\right)}^2}=0,\text{for}x\in {\Omega }_{x_0},$$ (89)

i.e.,

$$\frac{\partial h}{\partial x_1}\left(x\right)=\frac{\partial h}{\partial x_2}\left(x\right)=0,\text{for}x\in {\Omega }_{x_0}.$$ (90)

Therefore,

$$\frac{{\partial }^{2}h}{\partial {x_1}^2}\left(x\right)=\frac{{\partial }^{2}h}{\partial x_1\partial x_2}\left(x\right)=\frac{{\partial }^{2}h}{\partial {x_2}^2}\left(x\right)=0,\text{for}x\in {\Omega }_{x_0}.$$ (91)

This is in contradiction to Eq. (88). Eq. (85) implies that

$$\frac{{\partial }^{2}h}{\partial {x_1}^2}\left(x\right)=\frac{{\partial }^{2}h}{\partial x_1\partial x_2}\left(x\right)=\frac{{\partial }^{2}h}{\partial {x_2}^2}\left(x\right)=0,\text{for}x\in {\Omega }_a\backslash \bigcup _{i=1}^m\bigcup _{j>i,j\in N_i}{\Gamma }_{i,j}.$$ (92)

Because f₀(x) is a piecewise linear function in Ω_a, it follows from Eq. (92) that

$$\frac{{\partial }^{2}u}{\partial {x_1}^2}\left(x\right)=\frac{{\partial }^{2}u}{\partial x_1\partial x_2}\left(x\right)=\frac{{\partial }^{2}u}{\partial {x_2}^2}\left(x\right)=0,\text{for}x\in {\Omega }_a\backslash \bigcup _{i=1}^m\bigcup _{j>i,j\in N_i}{\Gamma }_{i,j}.$$ (93)

Due to the analyticity of u(x) by Theorem 1, we have

$$\frac{{\partial }^{2}u}{\partial {x_1}^2}\left(x\right)=\frac{{\partial }^{2}u}{\partial x_1\partial x_2}\left(x\right)=\frac{{\partial }^{2}u}{\partial {x_2}^2}\left(x\right)=0,\text{for}x\in {\Omega }_a.$$ (94)

Hence,

$$u\left(x\right)=a{x}_1+b{x}_2+c,\text{for}x\in {\Omega }_a.$$ (95)

By Theorem 2, we obtain u(x) = 0 and h(x = f₀(x).

Generally speaking, we assume that an object image f₀(x) is a piecewise n-th (some n ≥ 1) order polynomial function in Ω_a; that is, Ω_a can be decomposed into finitely many sub-domains ${\left\{{\Omega }_i\right\}}_{i=1}^m$ (Fig. 4) such that

$$f_0\left(x\right)=f_i\left(x\right),\text{for}x\in {\Omega }_i,1\le i\le m,$$ (96)

where f_i(x) is a n-th order polynomial function, and each sub-domain Ω_i is adjacent to its neighboring sub-domains Ω_j with piecewise smooth boundaries Γ_i,j, j ∈ N_i. We can similarly define the n+1-th order TV for any candidate image f(x) as follows:

$${\mathrm{HOT}}_{\mathrm{n}+1}\left(f\right)=\underset{\left(\underset{1\le k\le M}{\text{max}}diam\left\{Q_k\right\}\right)\to 0}{\text{lim sup}}\sum _{k=1}^M{I}_k\left(f\right),$$ (97)

where ${\left\{Q_k\right\}}_{k=1}^M$ is an arbitrary partition of Ω_a, and

$$I_k\left(f\right)=\text{min}\left(\underset{\theta \in S^1}{\text{sup}}\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{\int }_{Q_k}f\left(x\right)\frac{dg}{d\theta }\left(x\right)dx,\underset{\theta \in S^1}{\text{sup}}\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{\int }_{Q_k}f\left(x\right)\frac{d^{n+1}g}{d{\theta }^{n+1}}\left(x\right)dx\right),$$ (98)

where

$$\frac{d^{n+1}g}{d{\theta }^n}\left(x\right)=\frac{d^{n+1}{g}_{x,\theta }\left(t\right)}{d{t}^n}{\mid }_{t=0}.$$ (99)

We have the following generalized version of Lemma 4.

Lemma 5. Suppose that an object image f₀(x) is a piecewise n-th (n ≥ 1) order polynomial function in Ω_a, as defined by Eq. (96). For any candidate image f(x) = f₀(x) + u(x), we have

$${\mathrm{HOT}}_{\mathrm{n}+1}\left(f\right)=\sum _{i=1}^m\sum _{j>i,j\in N_i}{\int }_{{\Gamma }_{i,j}}\mid f_i\left(x\right)-f_j\left(x\right)\mid ds+{\int }_{{\Omega }_a}\text{min}\left(\underset{\theta \in S^1}{\text{max}}\mid \frac{df}{d\theta }\left(x\right)\mid ,\underset{\theta \in S^1}{\text{max}}\mid \frac{d^{n+1}f}{d{\theta }^{n+1}}\left(x\right)\mid \right)d{x}_{1}d{x}_2,$$ (100)

where the second term is a Lebesgue integral.

Proof: We proceed by arguments similar to that for Lemma 4. Again, f(x) = f₀(x) + u(x), and u(x) is an analytic function. Let ${\left\{Q_k\right\}}_{k=1}^M$ be an arbitrary partition of Ω_a. First, let us consider Q_k covering the common boundary Γ_i,j of a pair of neighboring sub-domains Ω_i and Ω_j and is contained in ${\Omega }_i\cup {\Omega }_j$ (Fig. 5 (a)). As in the proof of Lemma 4, for $g\in C_0^{\infty }\left(Q_k\right)$ we have

$$\underset{\theta \in S^1}{\text{sup}}\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{\int }_{Q_k}f\left(x\right)\frac{dg}{d\theta }\left(x\right)dx={\int }_{{\Gamma }_{i,j}\cap Q_k}\mid f_j\left(x\right)-f_i\left(x\right)\mid ds+O\left(1\right)\mid Q_k\mid +o\left(1\right)\mid {\Gamma }_{i,j}\cap Q_k\mid .$$ (101)

Repeatedly performing 2-D integrations by parts, for $g\in C_0^{\infty }\left(Q_k\right)$ we have

$$\begin{array}{cc}\hfill & {\int }_{Q_k}f\left(x\right)\frac{d^{n+1}g}{d{\theta }^{n+1}}\left(x\right)dx={\int }_{Q_k\cap {\Omega }_i}f\left(x\right)\frac{d^{n+1}g}{d{\theta }^{n+1}}\left(x\right)dx+{\int }_{Q_k\cap {\Omega }_j}f\left(x\right)\frac{d^{n+1}g}{d{\theta }^{n+1}}\left(x\right)dx\hfill \\ \hfill & ={\int }_{{\Gamma }_{i,j}\cap Q_k}(f_j\left(x\right)-f_i\left(x\right))\frac{d^{n}g}{d{\theta }^n}\left(x\right)\text{cos}<\theta ,{\theta }_N>ds-{\int }_{Q_k\cap {\Omega }_i}\frac{df}{d\theta }\left(x\right)\frac{d^{n}g}{d{\theta }^n}\left(x\right)dx-{\int }_{Q_k\cap {\Omega }_j}\frac{df}{d\theta }\left(x\right)\frac{d^{n}g}{d{\theta }^n}\left(x\right)dx\hfill \\ \hfill & ={\int }_{{\Gamma }_{i,j}\cap Q_k}(f_j\left(x\right)-f_i\left(x\right))\frac{d^{n}g}{d{\theta }^n}\left(x\right)\text{cos}<\theta ,{\theta }_N>ds-{\int }_{{\Gamma }_{i,j}\cap Q_k}(\frac{d{f}_j}{d\theta }\left(x\right)-\frac{d{f}_i}{d\theta }\left(x\right))\frac{d^{n-1}g}{d{\theta }^{n-1}}\left(x\right)\text{cos}<\theta ,{\theta }_N>ds+{\int }_{Q_k\cap {\Omega }_i}\frac{d^{2}f}{d{\theta }^2}\left(x\right)\frac{d^{n-1}g}{d{\theta }^{n-1}}\left(x\right)dx+{\int }_{Q_k\cap {\Omega }_j}\frac{d^{2}f}{d{\theta }^2}\left(x\right)\frac{d^{n-1}g}{d{\theta }^{n-1}}\left(x\right)dx\hfill \\ \hfill & =\sum _{l=1}^n{(-1)}^l{\int }_{{\Gamma }_{i,j}\cap Q_k}(\frac{d^l{f}_j}{d{\theta }^l}\left(x\right)-\frac{d^l{f}_i}{d{\theta }^l}\left(x\right))\frac{d^{n-l}g}{d{\theta }^{n-l}}\left(x\right)\text{cos}<\theta ,{\theta }_N>ds+{(-1)}^{n+1}\left({\int }_{Q_k\cap {\Omega }_i}\frac{d^{n+1}f}{d{\theta }^{n+1}}\left(x\right)g\left(x\right)dx+{\int }_{Q_k\cap {\Omega }_j}\frac{d^{n+1}f}{d{\theta }^{n+1}}\left(x\right)g\left(x\right)dx\right)\hfill \\ \hfill & =\sum _{l=1}^{n-1}{(-1)}^l{\int }_{{\Gamma }_{i,j}\cap Q_k}(\frac{d^l{f}_j}{d{\theta }^l}\left(x\right)-\frac{d^l{f}_i}{d{\theta }^l}\left(x\right))\frac{d^{n-l}g}{d{\theta }^{n-l}}\left(x\right)\text{cos}<\theta ,{\theta }_N>ds+{(-1)}^n{\int }_{{\Gamma }_{i,j}\cap Q_k}(\frac{d^n{f}_j}{d{\theta }^n}\left(x\right)-\frac{d^n{f}_i}{d{\theta }^n}\left(x\right))g\left(x\right)\text{cos}<\theta ,{\theta }_N>ds+{(-1)}^{n+1}{\int }_{Q_k}\frac{d^{n+1}f}{d{\theta }^{n+1}}\left(x\right)g\left(x\right)dx,\hfill \end{array}$$ (102)

where θ_N is the normal vector of the boundary curve Γ_i,j pointing from Ω_j towards Ω_i, and <θ,θ_N > the angle between the vectors θ and θ_N. For the second term on the right-hand side of Eq. (102), we have

$$\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{(-1)}^n{\int }_{{\Gamma }_{i,j}\cap Q_k}(\frac{d^n{f}_j}{d{\theta }^n}\left(x\right)-\frac{d^n{f}_i}{d{\theta }^n}\left(x\right))g\left(x\right)\text{cos}<\theta ,{\theta }_N>ds={\int }_{{\Gamma }_{i,j}\cap Q_k}\mid \frac{d^n{f}_j}{d{\theta }^n}\left(x\right)-\frac{d^n{f}_i}{d{\theta }^n}\left(x\right)\mid \text{cos}<\theta ,{\theta }_N>ds,$$ (103)

$$\underset{\theta \in S^1}{\text{sup}}\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{(-1)}^n{\int }_{{\Gamma }_{i,j}\cap Q_k}(\frac{d^n{f}_j}{d{\theta }^n}\left(x\right)-\frac{d^n{f}_i}{d{\theta }^n}\left(x\right))g\left(x\right)\text{cos}<\theta ,{\theta }_N>ds={\int }_{{\Gamma }_{i,j}\cap Q_k}\underset{\theta \in S^1}{\text{max}}\left(\mid \frac{d^n{f}_j}{d{\theta }^n}\left(x\right)-\frac{d^n{f}_i}{d{\theta }^n}\left(x\right)\mid \text{cos}<\theta ,{\theta }_N>\right)ds+o\left(1\right)\mid {\Gamma }_{i,j}\cap Q_k\mid .$$ (104)

For the third term on the right-hand side of Eq. (102), we have

$${(-1)}^{n+1}{\int }_{Q_k}\frac{d^{n+1}f}{d{\theta }^{n+1}}\left(x\right)g\left(x\right)dx=O\left(1\right)\mid Q_k\mid .$$ (105)

We proceed to evaluate $\underset{\theta \in S^1}{\sup }\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\sup }{\int }_{Q_k}f\left(x\right)\frac{d^{n+1}g}{d{\theta }^{n+1}}\left(x\right)dx$ in the following two cases.

Case 1: If there exist some θ ∈ S¹ and some $x\in {\Gamma }_{i,j}\cap Q_k$ such that $\underset{0\le l\le n-1}{\max }\mid \frac{d^l{f}_j}{d{\theta }^l}\left(x\right)-\frac{d^l{f}_j}{d{\theta }^l}\left(x\right)\mid \ne 0$, then for an arbitrary real constant series ${\left\{C_l\right\}}_{l=1}^{n-1}$ and an arbitrary compact set $K\subset Q_k$, there exists a $g\in C_0^{\infty }\left(Q_k\right)$ satisfying |g(x) and

$$\frac{d^{n-l}g}{d{\theta }^{n-1}}\left(x\right)=C_l{(-1)}^l(\frac{d^l{f}_j}{d{\theta }^l}\left(x\right)-\frac{d^l{f}_i}{d{\theta }^l}\left(x\right)),\text{for}1\le l\le n-1,x\in {\Gamma }_{i,j}\cap K,\text{and}$$ (106)

we have

$$\underset{\theta \in S^1}{\text{sup}}\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}\sum _{l=1}^{n-1}{(-1)}^l{\int }_{{\Gamma }_{i,j}\cap Q_k}(\frac{d^l{f}_j}{d{\theta }^l}\left(x\right)-\frac{d^l{f}_i}{d{\theta }^l}\left(x\right))\frac{d^{n-1}g}{d{\theta }^{n-l}}\left(x\right)\text{cos}<\theta ,{\theta }_N>ds=+\infty .$$ (107)

Combining Eqs. (104), (105) and (107), we obtain

$$\underset{\theta \in S^1}{\text{sup}}\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{\int }_{Q_k}f\left(x\right)\frac{d^{n+1}g}{d{\theta }^{n+1}}\left(x\right)dx\ge \underset{\theta \in S^1}{\text{sup}}\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}\sum _{l=1}^{n-1}{(-1)}^l{\int }_{{\Gamma }_{i,j}\cap Q_k}(\frac{d^l{f}_j}{d{\theta }^l}\left(x\right)-\frac{d^l{f}_i}{d{\theta }^l}\left(x\right))\frac{d^{n-l}g}{d{\theta }^{n-l}}\left(x\right)\text{cos}<\theta ,{\theta }_N>ds-\underset{\theta \in S^1}{\text{sup}}\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{(-1)}^n{\int }_{{\Gamma }_{i,j}\cap Q_k}(\frac{d^n{f}_j}{d{\theta }^n}\left(x\right)-\frac{d^n{f}_i}{d{\theta }^n}\left(x\right))\text{cos}<\theta ,{\theta }_N>ds-\underset{\theta \in S^1}{\text{sup}}\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{\int }_{Q_k}\frac{d^{n+1}f}{d{\theta }^{n+1}}\left(x\right)g\left(x\right)dx=+\infty .$$ (108)

Case 2: Otherwise, $\frac{d^l{f}_j}{d{\theta }^l}\left(x\right)-\frac{d^l{f}_j}{d{\theta }^l}\left(x\right)=0$ for $x\in {\Gamma }_{i,j}\cap Q_k$, θ ∈ ^S1, 0 ≤ l ≤ n −1. The first term on the right-hand side of Eq. (102) equals 0. Then, we have

$$\underset{\theta \in S^1}{\text{sup}}\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{\int }_{Q_k}f\left(x\right)\frac{d^{n+1}g}{d{\theta }^{n+1}}\left(x\right)dx={\int }_{{\Gamma }_{i,j}\cap Q_k}\underset{\theta \in S^1}{\text{max}}\left(\mid \frac{d^n{f}_j}{d{\theta }^n}\left(x\right)-\frac{d^n{f}_i}{d{\theta }^n}\left(x\right)\mid \text{cos}<\theta ,{\theta }_N>\right)ds+O\left(1\right)\mid Q_k\mid +o\left(1\right)\mid {\Gamma }_{i,j}\cap Q_k\mid .$$ (109)

In this case we also have

$${\int }_{{\Gamma }_{i,j}\cap Q_k}\mid f_j\left(x\right)-f_i\left(x\right)\mid ds=0,$$ (110)

$$\underset{\theta \in S^1}{\text{sup}}\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{\int }_{Q_k}f\left(x\right)\frac{dg}{d\theta }\left(x\right)dx={\int }_{{\Gamma }_{i,j}\cap Q_k}\mid f_j\left(x\right)-f_i\left(x\right)\mid ds+O\left(1\right)\mid Q_k\mid +o\left(1\right)\mid {\Gamma }_{i,j}\cap Q_k\mid =O\left(1\right)\mid Q_k\mid +o\left(1\right)\mid {\Gamma }_{i,j}\cap Q_k\mid .$$ (111)

Combining Eqs. (108), (109) and (111), we have the following conclusion: If Q_k covers the common boundary Γ_i,j of a pair of neighboring sub-domains Ω_i and Ω_j and is contained in ${\Omega }_i\cup {\Omega }_j$, then

$$\begin{array}{cc}\hfill & I_k\left(f\right)=\text{min}\left(\underset{\theta \in S^1}{\text{sup}}\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{\int }_{Q_k}f\left(x\right)\frac{dg}{d\theta }\left(x\right)dx,\underset{\theta \in S^1}{\text{sup}}\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{\int }_{Q_k}f\left(x\right)\frac{d^{n+1}g}{d{\theta }^{n+1}}\left(x\right)dx\right)\hfill \\ \hfill & =\underset{\theta \in S^1}{\text{sup}}\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{\int }_{Q_k}f\left(x\right)\frac{dg}{d\theta }\left(x\right)dx\hfill \\ \hfill & ={\int }_{{\Gamma }_{i,j}\cap Q_k}\mid f_j\left(x\right)-f_i\left(x\right)\mid ds+O\left(1\right)\mid Q_k\mid +o\left(1\right)\mid {\Gamma }_{i,j}\cap Q_k\mid .\hfill \end{array}$$ (112)

Next, Let us consider Q_k that is completely contained in some sub-domain Ω_i (Fig. 5 (b)). For $g\in C_0^{\infty }\left(Q_k\right)$, performing 2-D integration by parts we have

$${\int }_{Q_k}f\left(x\right)\frac{dg}{d\theta }\left(x\right)dx=-{\int }_{Q_k}\frac{df}{d\theta }\left(x\right)g\left(x\right)dx,$$ (113)

$${\int }_{Q_k}f\left(x\right)\frac{d^{n+1}g}{d{\theta }^{n+1}}\left(x\right)dx={(-1)}^{n+1}{\int }_{Q_k}\frac{d^{n+1}f}{d{\theta }^{n+1}}\left(x\right)g\left(x\right)dx.$$ (114)

Hence,

$$\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{\int }_{Q_k}f\left(x\right)\frac{dg}{d\theta }\left(x\right)dx={\int }_{Q_k}\mid \frac{df}{d\theta }\left(x\right)\mid dx,$$ (115)

$$\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{\int }_{Q_k}f\left(x\right)\frac{d^{n+1}g}{d{\theta }^{n+1}}\left(x\right)dx={\int }_{Q_k}\mid \frac{d^{n+1}f}{d{\theta }^{n+1}}\left(x\right)\mid dx.$$ (116)

Furthermore,

$$\underset{\theta \in S^1}{\text{sup}}\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{\int }_{Q_k}f\left(x\right)\frac{dg}{d\theta }\left(x\right)dx={\int }_{Q_k}\underset{\theta \in S^1}{\text{max}}\mid \frac{df}{d\theta }\left(x\right)\mid dx+o\left(1\right)\mid Q_k\mid ,$$ (117)

$$\underset{\theta \in S^1}{\text{sup}}\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{\int }_{Q_k}f\left(x\right)\frac{d^{n+1}g}{d{\theta }^{n+1}}\left(x\right)dx={\int }_{Q_k}\underset{\theta \in S^1}{\text{max}}\mid \frac{d^{n+1}f}{d{\theta }^{n+1}}\left(x\right)\mid dx+o\left(1\right)\mid Q_k\mid .$$ (118)

Combining Eqs. (117-118), we have

$$\begin{array}{cc}\hfill & I_k\left(f\right)=\text{min}\left(\underset{\theta \in S^1}{\text{sup}}\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{\int }_{Q_k}f\left(x\right)\frac{dg}{d\theta }\left(x\right)dx,\underset{\theta \in S^1}{\text{sup}}\underset{g\in C_0^{\infty }\left(Q_k\right),\mid g\left(x\right)\mid \le 1}{\text{sup}}{\int }_{Q_k}f\left(x\right)\frac{d^{n+1}g}{d{\theta }^{n+1}}\left(x\right)dx\right)\hfill \\ \hfill & =\text{min}\left({\int }_{Q_k}\underset{\theta \in S^1}{\text{max}}\mid \frac{df}{d\theta }\left(x\right)\mid dx,{\int }_{Q_k}\underset{\theta \in S^1}{\text{max}}\mid \frac{d^{n+1}f}{d{\theta }^{n+1}}\left(x\right)\mid dx\right)+o\left(1\right)\mid Q_k\mid \hfill \\ \hfill & ={\int }_{Q_k}\text{min}\left(\underset{\theta \in S^1}{\text{max}}\frac{df}{d\theta }\left(x\right)dx,\underset{\theta \in S^1}{\text{max}}\frac{d^{n+1}f}{d{\theta }^{n+1}}\left(x\right)\right)dx+o\left(1\right)\mid Q_k\mid .\hfill \end{array}$$ (119)

In Eqs. (113-119), we have utilized the fact that $\underset{\theta \in S^1}{\max }\frac{d^{n+1}f}{d{\theta }^{n+1}}\left(x\right)\nabla$ is continuous in each Ω_i(1 ≤ i ≤ m ). This fact can be derived from the following equation

$$\frac{d^{n+1}f}{d{\theta }^{n+1}}\left(x\right)={\left(\frac{\partial }{\partial x_1}\text{cos}\phi +\frac{\partial }{\partial x_2}\text{sin}\phi \right)}^{n+1}f\left(x\right)=\sum _{l=0}^{n+1}{C}_{n+1}^l\frac{{\partial }^{n+1}f}{\partial {x_1}^l\partial {x_2}^{n+1-l}}\left(x\right){\text{cos}}^l\phi {\text{sin}}^{n+1-l}\phi ,\text{for}x\in {\Omega }_i,1\le i\le m,\theta =(\text{cos}\phi ,\text{sin}\phi )\in S^1.$$ (120)

Combining Eqs. (112) and 119), we obtain

$$\sum _{k=1}^M{I}_k\left(f\right)=\sum _{i=1}^m\sum _{j>i,j\in N_i}{\int }_{{\Gamma }_{i,j}}\mid f_i\left(x\right)-f_j\left(x\right)\mid ds+{\int }_{{\Omega }_a}\text{min}\left(\underset{\theta \in S^1}{\text{max}}\mid \frac{df}{d\theta }\left(x\right)\mid ,\underset{\theta \in S^1}{\text{max}}\mid \frac{d^{n+1}f}{d{\theta }^{n+1}}\left(x\right)\mid \right)d{x}_{1}d{x}_2+O\left(1\right)\left(\sum _{i=1}^m\sum _{j>i,j\in N_i}\mid {\Gamma }_{i,j}\mid \right)\left(\underset{1\le k\le M}{\text{max}}diam\left\{Q_k\right\}\right)+o\left(1\right)\mid {\Omega }_a\mid .$$ (121)

Therefore, we have

$${\mathrm{HOT}}_2\left(f\right)=\underset{\left(\underset{1\le k\le M}{\text{max}}diam\left\{Q_k\right\}\right)\to 0}{\text{lim sup}}\sum _{k=1}^M{I}_k\left(f\right)=\sum _{i=1}^m\sum _{j>i,j\in N_i}{\int }_{{\Gamma }_{i,j}}\mid f_i\left(x\right)-f_j\left(x\right)\mid ds+{\int }_{{\Omega }_a}\text{min}\left(\underset{\theta \in S^1}{\text{max}}\mid \frac{df}{d\theta }\left(x\right)\mid ,\underset{\theta \in S^1}{\text{max}}\mid \frac{d^{n+1}f}{d{\theta }^{n+1}}\left(x\right)\mid \right)d{x}_{1}d{x}_2.$$ (122)

which completes the proof of Lemma 5.

Although it is difficult to have an explicit formula for $\underset{\theta \in S^1}{\max }\mid \frac{d^{n+1}f}{d{\theta }^{n+1}}\left(x\right)\mid$ with $x\in {\Omega }_a\backslash \bigcup _{i=1}^m\bigcup _{j>1,j\in N_i}{\Gamma }_{i,j}$ in the cases of n ≥ 2, we can still have the following Theorem as a generalized version of Theorem 4.

Theorem 5. Suppose that an object function f₀(x) is a piecewise n-th (n ≥1) order polynomial function in Ω_a, as defined by Eq. (80). If h(x) is a candidate image and ${\mathrm{HOT}}_{\mathrm{n}+1}\left(h\right)=\underset{f=f_0+u_1}{\min }{\mathrm{HOT}}_{\mathrm{n}+1}\left(f\right)$ where u₁(x) is an arbitrary ambiguity image, then h(x) = f₀(x) for x ∈ Ω_a.

Proof: We proceed by arguments similar to that for Theorem 4. Let h(x) = f₀(x) + u(x) for some ambiguity image u(x). By Lemma 5, we have

$${\mathrm{HOT}}_{\mathrm{n}+1}\left(f\right)\ge \sum _{i=1}^m\sum _{j>i,j\in N_i}{\int }_{{\Gamma }_{i,j}}\mid f_i\left(x\right)-f_j\left(x\right)\mid ds,\text{for}f=f_0\left(x\right)+u_1\left(x\right),$$ (123)

where u₁(x) is an arbitrary ambiguity image, and

$${\mathrm{HOT}}_{\mathrm{n}+1}\left(f_0\right)=\sum _{i=1}^m\sum _{j>i,j\in N_i}{\int }_{{\Gamma }_{i,j}}\mid f_i\left(x\right)-f_j\left(x\right)\mid ds.$$ (124)

Hence,

$$\underset{f=f_0+u_1}{\text{min}}{\mathrm{HOT}}_{\mathrm{n}+1}\left(f\right)=\sum _{i=1}^m\sum _{j>i,j\in N_i}{\int }_{{\Gamma }_{i,j}}\mid f_i\left(x\right)-f_j\left(x\right)\mid ds.$$ (125)

Because ${\mathrm{HOT}}_{\mathrm{n}+1}\left(h\right)=\underset{f=f_0+u}{\min }{\mathrm{HOT}}_{\mathrm{n}+1}\left(f\right)$, we have

$${\int }_{{\Omega }_a}{\int }_{{\Omega }_a}\text{min}\left(\underset{\theta \in S^1}{\text{max}}\mid \frac{dh}{d\theta }\left(x\right)\mid ,\underset{\theta \in S^1}{\text{max}}\mid \frac{d^{n+1}h}{d{\theta }^{n+1}}\left(x\right)\mid \right)d{x}_{1}d{x}_2=0.$$ (126)

Therefore,

$$\text{min}\left(\underset{\theta \in S^1}{\text{max}}\mid \frac{dh}{d\theta }\left(x\right)\mid ,\underset{\theta \in S^1}{\text{max}}\mid \frac{d^{n+1}h}{d{\theta }^{n+1}}\left(x\right)\mid \right)=0,\text{for}x\in {\Omega }_a\backslash \bigcup _{i=1}^m\bigcup _{j>i,j\in N_i}{\Gamma }_{i,j}.$$ (127)

That is,

$$\underset{\theta \in S^1}{\text{max}}\mid \frac{dh}{d\theta }\left(x\right)\mid =0\text{or}\underset{\theta \in S^1}{\text{max}}\mid \frac{d^{n+1}h}{d{\theta }^{n+1}}\left(x\right)\mid =0,\text{for}x\in {\Omega }_a\backslash \bigcup _{i=1}^m\bigcup _{j>i,j\in N_i}{\Gamma }_{i,j}.$$ (128)

We assert that

$$\underset{\theta \in S^1}{\text{max}}\mid \frac{d^{n+1}h}{d{\theta }^{n+1}}\left(x\right)\mid =0,\text{for}x=(x_1,x_2)\in {\Omega }_a\backslash \bigcup _{i=1}^m\bigcup _{j>i,j\in N_i}{\Gamma }_{i,j}.$$ (129)

Otherwise, there exists some $x_0\in {\Omega }_a\backslash \bigcup _{i=1}^m\bigcup _{j>1,j\in N_i}{\Gamma }_{i,j}$ such that

$$\underset{\theta \in S^1}{\text{max}}\mid \frac{d^{n+1}h}{d{\theta }^{n+1}}\left(x_0\right)\mid >0,$$ (130)

By continuity, there exists a neighborhoodof x₀ denoted by Ω_x0 such that

$${\Omega }_{x_0}\subset {\Omega }_a\backslash \bigcup _{i=1}^m\bigcup _{j>i,j\in N_i}{\Gamma }_{i,j},$$ (131)

and

$$\underset{\theta \in S^1}{\text{max}}\mid \frac{d^{n+1}h}{d{\theta }^{n+1}}\left(x\right)\mid >0,\text{for}x\in {\Omega }_{x_0}.$$ (132)

By Eq. (128), we have

$$\underset{\theta \in S^1}{\text{max}}\mid \frac{dh}{d\theta }\left(x\right)\mid =0,\text{for}x\in {\Omega }_{x_0},$$ (133)

e.g.,

$$\frac{dh}{d\theta }\left(x\right)=\frac{\partial h}{\partial x_1}\left(x\right)\text{cos}\phi +\frac{\partial h}{\partial x_2}\left(x\right)\text{sin}\phi =0,\text{for}x\in {\Omega }_{x_0},\theta =(\text{cos}\phi ,\text{sin}\phi )\in S^1.$$ (134)

From Eq.(134) we have

$$\frac{\partial h}{\partial x_1}\left(x\right)=\frac{\partial h}{\partial x_2}\left(x\right)=0,\text{for}x\in {\Omega }_{x_0}.$$ (135)

Therefore,

$$\frac{{\partial }^{n+1}h}{\partial {x_1}^l\partial {x_2}^{n+1-l}}\left(x\right)=0,\text{for}x\in {\Omega }_{x_0},0\le l\le n+1,$$ (136)

which leads to

$$\frac{d^{n+1}h}{d{\theta }^{n+1}}\left(x\right)=\sum _{l=0}^{n+1}{C}_{n+1}^l\frac{{\partial }^{n+1}h}{\partial {x_1}^l\partial {x_2}^{n+1-l}}\left(x\right){\text{cos}}^l\phi {\text{sin}}^{n+1-l}\phi =0,\text{for}x\in {\Omega }_{x_0},\theta =(\text{cos}\phi ,\text{sin}\phi )\in S^1.$$ (137)

Eq. (137) means that

$$\underset{\theta \in S^1}{\text{max}}\mid \frac{d^{n+1}h}{d{\theta }^{n+1}}\left(x\right)\mid =0,\text{for}x\in {\Omega }_{x_0}.$$ (138)

This is in contradiction to Eq. (132). Eq. (129) implies that

$$\frac{{\partial }^{n+1}h}{\partial {x_1}^l\partial {x_2}^{n+1-l}}\left(x\right)=0,\text{for}x\in {\Omega }_a\backslash \bigcup _{i=1}^m\bigcup _{j>i,j\in N_i}{\Gamma }_{i,j},0\le l\le n+1.$$ (139)

Because f₀(x) is a piecewise n-th (n ≥ 1) order polynomial function in Ω_a, it follows from Eq. (139) that

$$\frac{{\partial }^{n+1}h}{\partial {x_1}^l\partial {x_2}^{n+1-l}}\left(x\right)=0,\text{for}x\in {\Omega }_a\backslash \bigcup _{i=1}^m\bigcup _{j>i,j\in N_i}{\Gamma }_{i,j},0\le l\le n+1.$$ (140)

Due to the analyticity of u(x) by Theorem 1, we have

$$\frac{{\partial }^{n+1}h}{\partial {x_1}^l\partial {x_2}^{n+1-l}}\left(x\right)=0,\text{for}x\in {\Omega }_a,0\le l\le n+1.$$ (141)

Hence, u(x) is a n-th (n ≥ 1) order polynomial function in Ω_a. By Theorem 2, we obtain u(x) = 0 and h(x) = f₀(x).

IV. Numerical Simulation

To verify our theoretical findings described in the preceding section , we developed a HOT minimization based interior tomography algorithm. This iterative algorithm is a modification of our previously reported TV minimization based interior tomography algorithm [17]. Our HOT minimization algorithm consists of two major steps. In the first step, the ordered-subset simultaneous algebraic reconstruction technique (OS-SART) [23] is used to reconstruct a digital image f_m,n = f(mΔ,nΔ) based on all the available local projections, where Δ represents the sampling interval, m and n are integers. In the second step, the discrete HOT of f_m,n is minimized using the standard steepest descent method. These two steps are iteratively performed in an alternating manner. The major difference between this algorithm and that in [17] lies in the formulas for computing steepest descent directions. Here we assume that $\frac{{\partial }^{2}f}{\partial {x_1}^2}$, $\frac{{\partial }^{2}f}{\partial x_1\partial x_2}$, $\frac{{\partial }^{2}f}{\partial {x_2}^2}$ are continuous at x, and we have

$$\begin{array}{cc}\hfill & HO{T}_2={\int }_{{\Omega }_a}\left(\sqrt{\frac{1}{4}{\left(\frac{{\partial }^{2}f}{\partial {x_1}^2}-\frac{{\partial }^{2}f}{\partial {x_2}^2}\right)}^2+{\left(\frac{{\partial }^{2}f}{\partial x_1\partial x_2}\right)}^2}+\frac{1}{2}\mid \frac{{\partial }^{2}f}{\partial {x_1}^2}+\frac{{\partial }^{2}f}{\partial {x_2}^2}\mid \right)d{x}_{1}d{x}_2\hfill \\ \hfill & \doteq {\Delta }^2\sum _{m,n}\left(\sqrt{\frac{1}{4}{\left(\frac{f_{m+1,n}+f_{m-1,n}-f_{m,n+1}-f_{m,n-1}}{{\Delta }^2}\right)}^2+{\left(\frac{f_{m+1,n+1}+f_{m-1,n-1}-f_{m+1,n-1}-f_{m-1,n+1}}{4{\Delta }^2}\right)}^2}+\frac{1}{2}\mid \frac{f_{m+1,n}+f_{m-1,n}-2f_{m,n}}{{\Delta }^2}+\frac{f_{m,n+1}+f_{m,n-1}-2f_{m,n}}{{\Delta }^2}\mid \right)\hfill \\ \hfill & =\sum _{m,n}\left(\sqrt{{\left(\frac{f_{m+1,n}+f_{m-1,n}-f_{m,n+1}-f_{m,n-1}}{2}\right)}^2+{\left(\frac{f_{m+1,n+1}+f_{m-1,n-1}-f_{m+1,n-1}-f_{m-1,n+1}}{4}\right)}^2}+\mid \frac{f_{m+1,n}+f_{m-1,n}+f_{m,n+1}+f_{m,n-1}-4f_{m,n}}{2}\mid \right)\hfill \\ \hfill & =\sum _{m,n}\left(V_{m,n}^a+V_{m,n}^b\right),\hfill \end{array}$$ (142)

where

$$V_{m,n}^a=\sqrt{{\left(\frac{f_{m+1,n}+f_{m-1,n}-f_{m,n+1}-f_{m,n-1}}{2}\right)}^2+{\left(\frac{f_{m+1,n+1}+f_{m-1,n-1}-f_{m+1,n-1}-f_{m-1,n+1}}{4}\right)}^2},$$ (143)

$$V_{m,n}^b=\mid \frac{f_{m+1,n}+f_{m-1,n}+f_{m,n+1}+f_{m,n-1}-4f_{m,n}}{2}\mid .$$ (144)

Therefore,

$$\frac{\partial HO{T}_2}{\partial f_{m,n}}=D_{m+1,n}^{a,1}+D_{m-1,n}^{a,1}-D_{m,n+1}^{a,1}-D_{m,n-1}^{a,1}+D_{m+1,n+1}^{a,2}+D_{m-1,n-1}^{a,2}-D_{m+1,n-1}^{a,2}-D_{m-1,n+1}^{a,2},-4D_{m,n}^b+D_{m+1,n}^b+D_{m-1,n}^b+D_{m,n+1}^b+D_{m,n-1}^b,$$ (145)

where

$$D_{m,n}^{a,1}=\frac{\left(f_{m+1,n}+f_{m-1,n}-f_{m,n+1}-f_{m,n-1}\right)}{4V_{m,n}^a},$$ (146)

$$D_{m,n}^{a,2}=\frac{\left(f_{m+1,n+1}+f_{m-1,n-1}-f_{m+1,n-1}-f_{m-1,n+1}\right)}{16V_{m,n}^a},$$ (147)

$$D_{m,n}^b=\{\begin{array}{cc}0.5\hfill & if(f_{m+1,n}+f_{m-1,n}+f_{m,n+1}+f_{m,n-1}-4f_{m,n})\ge 0\hfill \\ -0.5\hfill & if(f_{m+1,n}+f_{m-1,n}+f_{m,n+1}+f_{m,n-1}-4f_{m,n})<0\hfill \end{array}\phantom{\}}.$$ (148)

For the other essential details of our algorithm, the reader may check[17].

A 2D Shepp-Logan phantom was modified to test our algorithm. The modified phantom included a set of piecewise linear ellipses with the parameters listed in Table 1. For each ellipse, the function was first defined inside a compact support ${\Omega }_e=\{(x_1,x_2)\in {\mathbb{R}}^2:\frac{x_1^2}{a_1^2}+\frac{x_2^2}{a_2^2}<1\}$ with the value $(\frac{x_{2}r}{a_2}+1)\mu$, then its center was translated to (x₁₀,x₂₀) and rotated by an angle ω. The units for a₁, a₂ and (x₁₀,x₂₀) were in mm and the unit for ω in degree.

Table 1.

Parameters of the 2D modified Shepp-Logan phantom.

No.	a1	a2	μ	r	x10	x20	ω
1	69.00	92.00	1.0	0	0	0	0
2	66.24	87.40	−0.8	0	0	−1.84	0
3	11.00	31.00	−0.1	1.0	22.00	0	−18.0
4	16.00	41.00	−0.1	1.0	−22.00	0	18.0
5	21.00	25.00	0.1	1.0	0	35.00	0
6	4.60	4.60	0.1	1.0	0	10.00	0
7	4.60	4.60	0.1	1.0	0	−10.00	0
8	4.60	2.30	0.1	1.0	−8.00	−60.50	0
9	2.30	2.30	0.1	1.0	0	−60.60	0
10	2.30	4.60	0.1	1.0	6.00	−60.60	0

In our numerical simulation, we assumed a circular scanning locus of radius 570 mm and a fan-beam imaging geometry. We used an equi-spatial detector array of length 100 mm. The detector was centered at the system origin and made always perpendicular to the direction from the system origin to the x-ray source. The detector array consisted of 300 elements, each of which had a 0.33 mm aperture. This configuration covered a circular field of view (FOV) of radius 49.8 mm. For a full scan, we equi-angularly collected 720 projections.

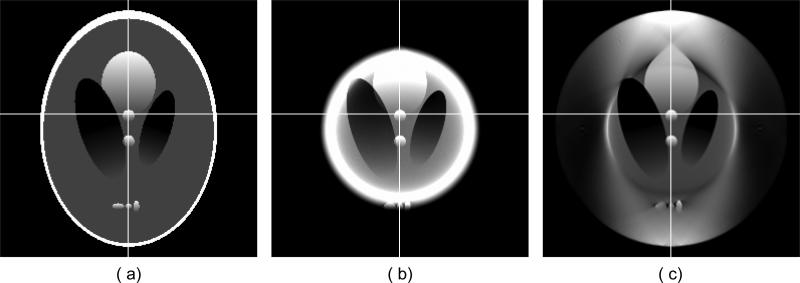
In the aforementioned FOV, we first created a high-resolution phantom image in a 2048×2048 matrix, and numerically generated truncated projections through an ROI using a well-known ray-tracing technique. Then, ROI images were reconstructed in a 256×256 matrix o using our proposed HOT minimization algorithm and a local FBP method from truncated projections after smooth extrapolation into missing data. Representative reconstructed images are in Fig. 6. The typical profiles are in Fig. 7. The convergence curves in terms of truncated projection discrepancy and relative reconstruction error are in Fig. 8. It can be seen in Figs. 6-8 that the reconstructed image using our proposed HOT minimization algorithm is in an excellent agreement with the truth inside the ROI.

Figure 6.

Reconstruction of the modified Shepp-Logan phantom with linearly varying shadings over subdomains. (a) The original phantom, (b) the reconstruction with the local FBP (after smooth data extrapolation), and (c) the reconstruction with the proposed HOT minimization algorithm after 40 iterations. The display window is [0.1, 0.4].

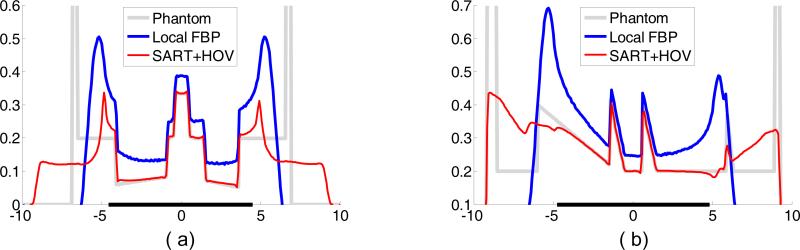
Figure 7.

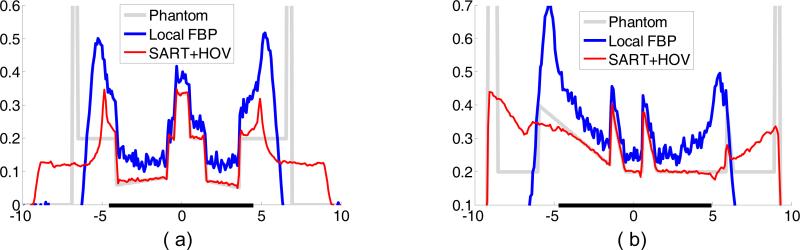
Representative profiles along (a) horizontal and (b) vertical lines in Figure 6. The horizontal and vertical axes represent the pixel coordinate and functional value respectively, with the thick line on the horizontal axis indicating the ROI.

Figure 8.

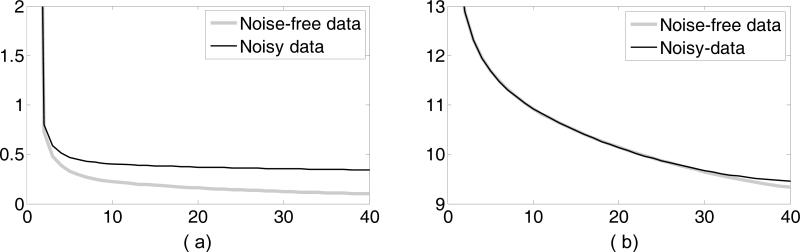
Convergence curves of the proposed HOT minimization algorithm. While the horizontal axis represents the iteration index, the vertical axis shows (a) the projection error and (b) reconstruction error (%) respectively.

To evaluate the noise characteristics and demonstrate the stability of our proposed HOT minimization algorithm, Poisson noise [24] was added to the simulated projection data. In this process, 10⁵ photons were emitted from the x-ray source towards each detector aperture. Then, we repeated the above reconstruction procedures and produced the typical images and profiles as shown in Figs. 9 and 10, along withthe convergence curves in Fig. 7. These figures demonstrate that the proposed algorithm not only produces satisfactory image accuracy but also suppresses image noise. This is not surprising, since the TV minimization technique was initially proposed to reduce noise [25].

Figure 9.

Counterpart of Figure 6, with data noise reflected in the local FBP and HOT minimization reconstructions. The display window is [0.1, 0.4].

Figure 10.

Counterpart of Figure 7, with data noise reflected in Figure 9 (b) and (c).

V. Discussions and Conclusion

In Theorem 5, we have claimed that if f₀(x) is a piecewise n-th (n ≥ 1) order polynomial function in Ω_a, then it can be uniquely determined by minimizing its (n+1)-th order HOT. To apply our theoretical result in practical applications, it is critical to estimate the maximum polynomials order n inside an ROI. In principle, there would be no problem if n is overestimated. Actually, as long as n captures the main features of image variations, even if it is underestimated, we can decompose f₀(x) into a n-th polynomial plus a residual error item much smaller than the primary term. Our hypothesis is that the reconstructed results can be written as the n-th polynomial plus a small artifact function. The higher the order n is, the smaller the artifact function becomes. When n is equal to or larger than the real polynomial order, the artifact function would be zero.

In practical applications, high order derivatives can be implemented as high order differences. Given the sensitivity of the discrete high order differencing operation, we suggest that the polynomial order be initially set to 1 ≤ n ≤ 3, and refined as needed. Note that in many cases we do have prior knowledge about images in a particular context. Hence, we can often estimate the polynomial order reliably. For example, in non-destructive testing machinery parts are fairly homogeneous, and the piecewise constant or piecewise linear assumption should work well.

As an important molecular imaging modality, single-photon emission computed tomography (SPECT) is to reconstruct a radioactive source distribution within a patient or animal. Different from the line integral model for x-ray imaging, SPECT projections are modeled as exponentially attenuated Radon transform data [26-28]. Extending x-ray interior tomography results [11-12], we previously proved that accurate and stable interior SPECT reconstruction is feasible from uniformly attenuated local projection data aided by prior knowledge of a sub-region [29]. Naturally, it would be useful to extend the theoretical results reported in this paper to SPECT. That is, it is possible to reconstruct a SPECT ROI accurately only from the uniformly attenuated local projections by minimizing the HOT if the distribution function is piecewise polynomial in the ROI. We are actively working along this direction.

To verify the correctness of our theoretical analysis in Section III, we have developed an iterative algorithm in Section IV. Nevertheless, our numerical implementation has been relatively preliminary. Neither the codes nor the control parameters have been optimized. Currently, we are developing efficient yet robust algorithms for real-world applications. In particular, we may merge the HOT minimization and iterative reconstruction into a more integrated procedure. Hopefully, we will be able to report more in follow-up papers. A theoretically interesting topic is about the convergence of the proposed algorithm. Previously, we studied the convergence of the well-known SART technique [30], and a general Landweber scheme [23] [30]. Although these results are relevant to the proposed algorithm, its convergence analysis may be much more challenging, and will be investigated in the future.

In conclusion, we have extended our TV minimization based interior tomography into a HOT minimization framework. Our work has indicated that an interior ROI can be accurately reconstructed from truncated projection data through the ROI if it can be partitioned into finitely many sub-domains over each of which a polynomial function well represents the image to be reconstructed. This HOT approach may find important applications in biomedical CT such as cardiac perfusion studies, and could inspire development of other imaging modalities as well.