Supplemental Analysis on Compressed Sensing Based Interior Tomography

Abstract

Recently, in the compressed sensing framework we proved that an interior ROI can be exactly reconstructed via the total variation minimization if the ROI is piecewise constant. In the proofs, we implicitly utilized the property that if an artifact image assumes a constant value within the ROI then this constant must be zero. Here we prove this property in the space of square integrable functions.

I. Background

It is well known that an interior region-of-interest (ROI) cannot be uniquely reconstructed from projection data only associated with lines through the ROI. Interestingly, our group and others independently established that this interior problem can be exactly and stably solved if a sub-region in the ROI is precisely known (Ye et al., 2007; Yu et al., 2008; Courdurier et al., 2008; Kudo et al., 2008). Recently, in the compressed sensing framework we proved that an interior ROI can be exactly reconstructed via the total variation minimization if the imaging object is piecewise constant (Yu and Wang, 2009; Han et al., 2009). In our proofs of Theorems 2.2 and 2.3, after we made the conclusion that the minimum was achieved at λ = 0 in (Yu and Wang, 2009) we implicitly utilized the property that if an artifact image assumes a constant value within the ROI then this constant must be zero. Here we provide a proof for this property so that our compressed sensing based interior tomography theory is expressed rigorously.

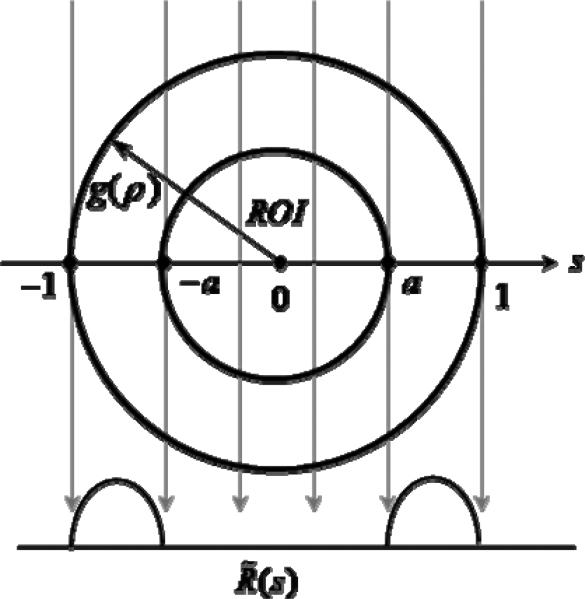
Let us consider a 2D smooth image f(ρ,θ), ρ∈[0,1], θ∈[0,2π) on a compact support within a unit disk Ω . The Radon transform of f(ρ,θ) can be written as R(s,φ), s ∈[–1,1], φ∈[0,π) . Suppose that we are only interested in reconstructing its interior part defined as ρ<a (0<a<1) from the corresponding local Radon transform data R(s,φ),|s|<a , which is also referred to as purely local projections. Based on the classic analysis, given these local data there is in general no unique solution (Natterer, 2001). Thus, any reconstructed image from such a local dataset can be viewed as a superposition of the exact reconstruction from a complete dataset R(s,φ),s∈[–1,1],φ∈[0,π) and an artificial reconstruction, which is an artifact image corresponding to another projection dataset R̃(s,φ), a <|s|≤1,φ∈[0,π) . Although R̃(s,φ)=0 for |s|<a, it can still produce a non-zero 2D local image g(ρ,θ), ρ∈[0,a), θ∈[0,2π) , inside the ROI. That is why we have the non-uniqueness of this interior problem (Natterer, 2001). It is well known that g(ρ,θ) is smooth and bounded inside the ROI if R̃(s,φ) is continuous and bounded. Previously, we proved that both $\frac{\partial g(\rho ,\theta )}{\partial \rho }$ and $\frac{\partial g(\rho ,\theta )}{\rho \partial \theta }$ are smooth and bounded inside the ROI (Yu and Wang, 2009). In the this note we will prove that g(ρ,θ)≡C for ρ∈[0,a) if and only if C=0.

The organization of this report is as follows. In the next section, we first prove that the constant C must be zero in the symmetric case using Taylor's expansion technique and Weierstrass's approximation theorem, and then extend it to the general non-symmetric case. In the third section, we numerically verify that a non-zero constant cannot satisfy the so-called Picard condition in the framework of singular value decomposition. In the last section, we discuss the relationship between this report and our previous work as well as future directions

II. Theoretical Analysis

Assuming that a circularly symmetric artifact image g(ρ,θ)=g(ρ) is reconstructed from a projection dataset R̃(s,φ) = R̃\(s) (a <|s|≤1,φ∈[0,π)) and R̃(s)≡0 for s ∈[–a,a] (Figure 1) and g(ρ)≡C (ρ∈[0,a) ), where C is a non-zero constant. Then, by the definition of the line integral we must have the following relationship for g(ρ) (ρ∈[a,1]):

$$\tilde{R}\left(s\right)={\int }_a^{1}g\left(\rho \right)d\sqrt{{\rho }^2-s^2}+C\sqrt{a^2-s^2}={\int }_a^1\frac{\rho g\left(\rho \right)d\rho }{\sqrt{{\rho }^2-s^2}}+C\sqrt{a^2-s^2}=0,s\in [0,a].$$ (1)

Figure 1.

Circularly symmetric artifact image g.

Our main theoretical results are as follows.

Theorem 2.1. Assuming that a circularly symmetric artifact image g(ρ,θ) = g(ρ) is reconstructed from a projection dataset R̃(s,φ)=R̃(s) (|s|≤1,φ∈[0,π)) and R̃(s) ≡ 0 for s ∈[–a,a]. If g(ρ) is a square integrable function on [0,1] with g(ρ)≡C (ρ∈[0,a) ), then C=0.

Proof: Eq. (1) can be changed to

$$Ca\sqrt{1-{(s∕a)}^2}+{\int }_a^1\frac{g\left(\rho \right)d\rho }{\sqrt{1-{(s∕\rho )}^2}}=0,0\le s\le a.$$ (2)

Denote (2k–1)!!=1×3×5---× (2k–1) and k!=1×2×3---×k, we have the following Taylor's expansions

$$\frac{1}{\sqrt{1-{(s∕\rho )}^2}}=1+\sum _{k=1}^{\infty }\frac{(2k-1)!!}{2^{k}k!}{\left(\frac{s}{\rho }\right)}^{2k},$$ (3)

$$\sqrt{1-{(s∕a)}^2}=1-\frac{1}{2k-1}\sum _{k=1}^{\infty }\frac{(2k-1)!!}{2^{k}k!}{\left(\frac{s}{a}\right)}^{2k}.$$ (4)

Inserting Eqs. (3) and (4) into Eq. (2), we have

$${\int }_a^{1}g\left(\rho \right){(a∕\rho )}^{2k}d\rho =\frac{Ca}{2k-1},k\ge 0.$$ (5)

Making the variable transformation t=a/ρ, Eq. (5) becomes

$${\int }_a^{1}g(a∕t)t^{2k-2}dt=\frac{C}{2k-1},k\ge 0.$$ (6)

Let

$$\tilde{g}\left(t\right)=\{\begin{array}{cc}g(a∕t)-C\hfill & t\in [a,1]\hfill \\ -C\hfill & t\in [0,a)\hfill \end{array}\phantom{\}},$$ (7)

Eq. (6) implies

$${\int }_0^1\tilde{g}\left(t\right)t^{2k}dt=0,k\ge 0.$$ (8)

Considering the even function ĝ(t)=(g̃(|t|) on the interval [–1,1], we have

$${\int }_{-1}^1\widehat{g}\left(t\right)t^{k}dt=0,k\ge 0.$$ (9)

By Weierstrass's approximation theorem and the fact that the continuous function space is dense in the square integrable function space on [–1,1], there exist a polynomial series ${\left\{p_n\left(t\right)\right\}}_{n=1}^{\infty }$ on interval [–1,1] such that

$${\int }_{-1}^1{\mid \widehat{g}\left(t\right)-P_n\left(t\right)\mid }^{2}dt\le \frac{1}{n}.$$ (10)

This leads to

$${\int }_{-1}^1{\widehat{g}}^2\left(t\right)dt=\underset{n\to \infty }{\text{lim}}{\int }_{-1}^1\widehat{g}\left(t\right)p_n\left(t\right)dt=0.$$ (11)

Hence, ĝ(t)=0 almost everywhere on [–1,1], which implies C= 0.

The above theorem can be extended to the general non-symmetric case.

Theorem 2.2. Assuming that a circularly non-symmetric artifact image g(ρ,θ) is reconstructed from a projection dataset R̃(s,φ) (|s|≤1,φ∈[0,π) ) and R̃(s,φ)≡0 for s∈[–a,a]. If g(ρ,θ) is a square integrable function on ρ∈[0,1] and θ∈[0,2π] with g(ρ,θ)≡C (ρ∈[0,a) ), then C=0.

Proof: Let us denote g(ρ,θ) in the Cartesian coordinates as g_d(x, y) with x = ρcosθ and y = ρsinθ. Define $\stackrel{‒}{g}(\rho ,\theta )=\frac{1}{2\pi }{\int }_0^{2\pi }g(\rho ,\theta +\varphi )d\varphi$, correspondingly we have

$$\begin{array}{cc}\hfill {\stackrel{‒}{g}}_d(x,y)& =\frac{1}{2\pi }{\int }_0^{2\pi }{g}_d(\rho \text{cos}(\theta +\varphi ),\rho \text{sin}(\theta +\varphi ))d\varphi \hfill \\ \hfill & =\frac{1}{2\pi }{\int }_0^{2\pi }{g}_d(x\text{cos}\varphi -y\text{sin}\varphi ,x\text{sin}\varphi +y\text{cos}\varphi )d\varphi .\hfill \end{array}$$ (12)

Clearly, ḡ(ρ,θ) is a circularly symmetric square integrable function and satisfies ḡ(ρ,θ)≡C (ρ∈[0,a) ). For s ∈[–a,a] the Radon transform R̄(s,φ) of ḡ(ρ,θ) can be expressed as

$$\begin{array}{cc}\hfill \stackrel{‒}{R}(s,\phi )& ={\int }_{-\sqrt{1-s^2}}^{\sqrt{1-s^2}}{\stackrel{‒}{g}}_d(s(\text{cos}\phi ,\text{sin}\phi )+t(-\text{sin}\phi ,\text{cos}\phi ))dt\hfill \\ \hfill & ={\int }_{-\sqrt{1-s^2}}^{\sqrt{1-s^2}}{\stackrel{‒}{g}}_d(s\text{cos}\phi -t\text{sin}\phi ,s\text{sin}\phi +t\text{cos}\phi )dt\hfill \\ \hfill & ={\int }_{-\sqrt{1-s^2}}^{\sqrt{1-s^2}}\left(\frac{1}{2\pi }{\int }_0^{2\pi }{g}_d(s\text{cos}(\phi +\varphi )-t\text{sin}(\phi +\varphi ),s\text{sin}(\phi +\varphi )+t\text{cos}(\phi +\varphi ))d\varphi \right)dt\hfill \\ \hfill & =\frac{1}{2\pi }{\int }_0^{2\pi }\left({\int }_{-\sqrt{1-s^2}}^{\sqrt{1-s^2}}{g}_d(s\text{cos}(\phi +\varphi )-t\text{sin}(\phi +\varphi ),s\text{sin}(\phi +\varphi )+t\text{cos}(\phi +\varphi ))dt\right)d\varphi \hfill \\ \hfill & =\frac{1}{2\pi }{\int }_0^{2\pi }\left({\int }_{-\sqrt{1-s^2}}^{\sqrt{1-s^2}}{g}_d(s(\text{cos}(\phi +\varphi ),\text{sin}(\phi +\varphi ))+t(-\text{sin}(\phi +\varphi ),\text{cos}(\phi +\varphi )))dt\right)d\varphi \hfill \\ \hfill & =\frac{1}{2\pi }{\int }_0^{2\pi }\tilde{R}(s,\phi +\varphi )d\varphi =0,\hfill \end{array}$$ (13)

where Eq.(12) has been used. By Theorem 2.1., we have C=0.

Remark: For real-world applications, all the reconstructed CT artifact images are bounded function and hence square integrable. Therefore, our assumption of square integrable functions can cover all the practical cases.

III. Numerical Analysis

Assuming that an integral kernel K(s,ρ) defined on I_s×I_ρ is continuous, square integrable and non-degenerate, by means of the singular value expansion (see Chapter 1.2.1 in (Hansen, 1998) ), we have

$$K(s,\rho )=\sum _{i=1}^{\infty }{\sigma }_i{u}_i\left(s\right)v_i\left(\rho \right),$$ (14)

where σ₁ ≥σ₂ ≥---> 0 , and u_i(s) and v_i(ρ) are orthonormal basis functions with respect to the conventional inner product

$$\left(u_i,u_j\right)={\int }_{I_s}{u}_i\left(t\right)u_j\left(t\right)d=\{\begin{array}{cc}1\hfill & \text{if}i=j\hfill \\ 0\hfill & \text{if}i\ne j\hfill \end{array}\phantom{\}},$$ (15)

and

$$\left(v_i,v_j\right)={\int }_{I_{\rho }}{v}_i\left(t\right)v_j\left(t\right)dt=\{\begin{array}{cc}1\hfill & \text{if}i=j\hfill \\ 0\hfill & \text{if}i\ne j\hfill \end{array}\phantom{\}}.$$ (16)

For any continuous and square integral function q(s), s∈I_s, the Fredholm integral equation of the first kind

$${\int }_{I_{\rho }}K(s,\rho )g\left(\rho \right)d\rho =q\left(s\right)$$ (17)

can be expressed as

$$\sum _{i=1}^{\infty }{\sigma }_i(v_i,g)u_i\left(s\right)=\sum _{i=1}^{\infty }(u_i,q)u_i\left(s\right),s\in I_s.$$ (18)

If there exists solutions for Eq. (17), one of them would be in the following form:

$$g\left(\rho \right)=\sum _{i=1}^{\infty }\frac{(u_i,q)}{{\sigma }_i}{v}_i\left(\rho \right),\rho \in I_{\rho }.$$ (19)

Eqs. (18) and (19) hold for uniform convergence (see Chapter 2.4 and Theorem 8.3.2 in (Smithies, 1958)). Although K(s,ρ) and q(s) are continuous and square integrable, g(ρ) expressed by Eq. (19) is not necessarily continuous or square integrable. In order that there exists a square integrable solution g(ρ) to Eq. (17), the right side of Eq. (19) must satisfy the Picard condition (see Chapter 1.2.3 in (Hansen, 1998)):

$$\sum _{i=1}^{\infty }{\left(\frac{(u_i,q)}{{\sigma }_i}\right)}^2<\infty .$$ (20)

This means that the (u_i, q) must decay faster than the singular value σ_i. This requirement is identical to that q(s) must belong to the range of the kernel K(s,ρ).

Let $K(s,\rho )=\frac{\rho }{\sqrt{{\rho }^2-s^2}}$, I_ρ = [a, 1], I_s = [0, a] and $q\left(s\right)=-C\sqrt{a^2-s^2}$, Eq. (1) can be considered as a a Fredholm integral equation of the first kind as defined in Eq. (17). If there exists a square integrable solution g(ρ) to Eq. (1), it should satisfy the Picard condition. However, it is not easy to perform a thorough theoretical analysis to verify the Picard condition for our problem. Nevertheless, the discrete Picard condition is often used in practical applications to study the existence of a solution to Eq. (17) using the singular value decomposition (SVD) approach. As pointed out by Hansen (Hansen, 1988), although a discrete Picard condition does not exist in a strict mathematical sense, it is certainly informative when numerically solving a Fredholm integral equation of the first kind Eq.(17).

In our case, let us discrete s as $s_n=\frac{a(n-0.5)}{N}$, n = 1,2,---,N and ρ as ${\rho }_m=a+\frac{(m-0.5)(1-a)}{M}$, m = 1,2,---,M. Accordingly, K(s,ρ), g(ρ) and q(s) are discretized as K(s_n,ρ_m), g(ρ_m), q(s_n). Hence, we have

$$\mathbf{KG}=\mathbf{Q},$$ (21)

where

$$\mathbf{K}=\frac{1-a}{M}\left(\begin{array}{ccccc}\hfill K(s_1,{\rho }_1)\hfill & \hfill \cdots \hfill & \hfill K(s_1,{\rho }_m)\hfill & \hfill \cdots \hfill & \hfill K(s_1,{\rho }_M)\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill K(s_n,{\rho }_1)\hfill & \hfill \cdots \hfill & \hfill K(s_n,{\rho }_m)\hfill & \hfill \cdots \hfill & \hfill K(s_n,{\rho }_M)\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill K(s_N,{\rho }_1)\hfill & \hfill \cdots \hfill & \hfill K(s_N,{\rho }_m)\hfill & \hfill \cdots \hfill & \hfill K(s_N,{\rho }_M)\hfill \end{array}\right),$$ (22)

$$\mathbf{G}={(g\left({\rho }_1\right)\cdots g\left({\rho }_m\right)\cdots g\left({\rho }_M\right))}^T,$$ (23)

and

$$\mathbf{Q}={(q\left(s_1\right)\cdots q\left(s_n\right)\cdots q\left(s_N\right))}^T.$$ (24)

Let M=N, the matrix K has the following SVD form (Hansen, 1988):

$$\mathbf{K}=\mathbf{U}\Lambda {\mathbf{V}}^T=\sum _{m=1}^M{\sigma }_m{\mathbf{u}}_m{\mathbf{v}}_m^T,$$ (25)

where U=(u₁ --- u_m --- u_M) and V = (v₁ --- v_m --- v_M) are orthogonal matrices, and Λ is a diagonal matrix whose diagonal elements satisfying σ₁≥σ₂≥---≥ 0. The solution to Eq. (20) can be written as

$$\mathbf{G}=\sum _{i=m}^M\frac{{\mathbf{u}}_m^T\mathbf{Q}}{{\sigma }_m}{\mathbf{v}}_m.$$ (26)

According to the Picard condition, we can compute $\mid \frac{{\mathbf{u}}_m^T\mathbf{Q}}{{\sigma }_m}\mid$ to test the existence of a solution to Eq. (1).

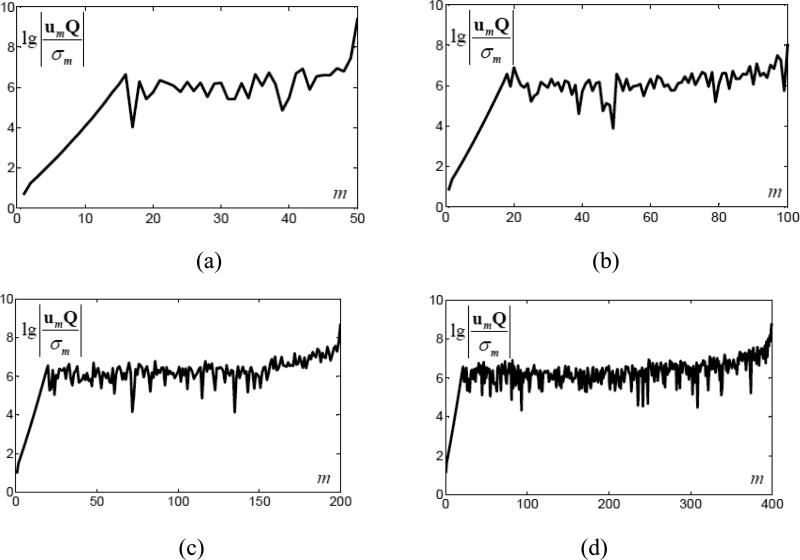
Without loss of generality, we set a=0.5 and $q\left(s\right)=\sqrt{a^2-s^2}$. For different combinations of sampling point numbers M and N, we computed and plotted $\lg \mid \frac{{\mathbf{u}}_m^T\mathbf{Q}}{{\sigma }_m}\mid$ in Figure 2, which clearly show that the singular value σ_m decays faster than ${\mathbf{u}}_m^T\mathbf{Q}$, suggesting that there is no square integrable solution for C ≠ 0 because any non-zero constant does not lead to a sufficiently fast decay of ${\mathbf{u}}_m^T\mathbf{Q}$. These numerical results are consistent to our theoretical analysis in the preceding section that if g(ρ) is square integrable constrained by an interior scan dataset then we must have C = 0 in Eq. (1).

Figure 2.

Curves of $\lg \mid \frac{{\mathbf{u}}_m^T\mathbf{Q}}{{\sigma }_m}\mid$ for different sampling point numbers (a) M =N=50, (b) 100, (c) 200 and (d) 400, respectively.

IV. Discussions and Conclusion

Although we assumed that an object to be reconstructed was piecewise constant both inside and outside an ROI, the piecewise constancy is only needed inside the ROI in the proofs in (Yu and Wang, 2009; Han et al., 2009). In other words, the piecewise constancy outside the ROI is not necessary. Note that a generalized total variation minimization theorem was proved for compressed sensing based interior tomography in (Han et al., 2009), without involving the Dirac delta function. Because most objects in CT applications can be approximately modeled as piecewise constant, the piecewise constancy assumption is quite reasonable (Wang et al., 2004), and our compressed sensing based interior tomography approach is practically useful. Most importantly, our finding suggests a new direction of interior tomography, and may lead to powerful methods for better interior reconstruction. Currently, we are working to relax the piecewise constancy assumption so that real-world images can be modeled with higher accuracy for new interior reconstruction results.

As discussed in (Yu and Wang, 2009), the key idea of compressed sensing based interior tomography is to define an appropriate sparsifying transform and an associated objective function. Then, the minimization of the objective function will lead to the true ROI image without any ambiguity. For that purpose, the most important step is to prove that the artifact image inside the ROI must be zero when its total variation is zero. Actually, it might appear in (Yu and Wang, 2009) that the artifact image inside the ROI can be any constant when the total variation is zero. Hence, it is the major contribution of this report that has proved the constant being necessarily zero, providing the uniqueness of our interior reconstruction. Using this methodology, we are working to extend compressed sensing based interior reconstruction under different conditions and for other modalities.

In conclusion, we have studied the characteristic of the artifact image inside an interior ROI subject to the local projection data constraint. Our theoretical and numerical analysis has demonstrated that the artifact image inside the ROI can be expressed as a constant if and only if the constant is zero. This analysis has consolidated our proofs of Theorems 2.2 and 2.3 in (Yu and Wang, 2009).