Calculating Partition Coefficients of Chain Anchors in Liquid-Ordered and Liquid-Disordered Phases

Abstract

We calculate partition coefficients of various chain anchors in liquid-ordered and liquid-disordered phases utilizing a theoretical model of a bilayer membrane containing cholesterol, dipalmitoyl phosphatidylcholine, and dioleoylphosphatidylcholine. The partition coefficients are calculated as a function of chain length, degree of saturation, and temperature. Partitioning depends on the difference between the lipid environments of the coexisting phases in which the anchors are embedded. Consequently, the partition coefficient depends on the nature of the anchor, and on the relative compositions of the coexisting phases. We find that saturated anchors prefer the denser liquid-ordered phase, and that the fraction of anchors in the liquid-ordered phase increases with increasing degree of saturation of the anchors. The partition coefficient also depends upon the location of the double bonds. Anchors with double bonds closer to the middle of the chain have a greater effect on partitioning than those near the end. Doubling the number of saturated chains increases the partitioning into the liquid-ordered phase for tails that are nearly as long or longer than those comprising the bilayer. Partitioning of such chains increases with decreasing temperature, indicating that energy considerations dominate entropic ones. In contrast, partitioning of shorter chains increases with increasing temperature, indicating that entropic considerations dominate.

Introduction

One of the most interesting, and controversial, models of biological membranes posits that they are not compositionally homogeneous, but that aggregates of saturated lipids and cholesterol float, like rafts, in a sea of unsaturated lipids (1–6). A further hypothesis is that the rafts and the sea are in fact domains of two coexisting phases denoted liquid-ordered (lo) and liquid-disordered (ld), respectively (7). Coexistence of two liquid phases is, indeed, commonly observed in model membranes that consist of a ternary mixture of saturated and unsaturated lipids and cholesterol (8). One reason for the great interest in this picture is that an inhomogeneous membrane would provide a substrate within which different proteins would be enriched, either in the rafts or in the sea, thereby increasing their efficacy. This enrichment follows from the different hydrocarbon chains that anchor many membrane proteins: extracellular anchors attached to the membrane via a glycophosphatidylinositol anchor that bury two such chains into the noncytoplasmic monolayer, intracellular anchors attached to the cytoplasmic monolayer by means of a single chain often derived from saturated myristic or palmitic acid, or from a bulky and unsaturated prenyl group. Presumably saturated anchors prefer the environment of the raft (i.e., liquid-ordered phase), rich as it is in saturated lipids, whereas unsaturated and/or otherwise bulky anchors prefer the environment of the sea of unsaturated lipids (i.e., liquid-disordered phase). To test this hypothesis, systems of lipids and lipidated peptides have been studied to determine the effect of lipid chain length, degree of unsaturation, etc., on the peptides' partition coefficient, i.e., the ratio of their concentration in the lo phase to that in the coexisting ld phase (9–15). These studies have found that the partitioning into the lo phase is greatest for saturated multichain anchors. The partitioning increases with increasing degree of saturation and/or number of saturated chains. The results also indicate that temperature has a greater effect on the partitioning of longer carbon chain anchors (16).

As intriguing as the phase-separation hypothesis is for understanding the heterogeneity of biological membranes, there are several competing theories. (Two excellent reviews on this topic can be found in Hancock (17) and Semrau and Schmidt (18) and their cited references.) One suggestion is that rafts be identified with the fluctuations that arise in a ternary fluid mixture that contains an interfacially active agent, as in a microemulsion (17,19,20). Another arises from a recent experiment (21), which suggests that membranes could be close to a miscibility critical point. This would imply the existence of strong composition fluctuations within the system: fluctuations that could be identified as rafts. The existence of a critical point suggests another possibility. Suppose that the system were in a one-phase region, say the ld phase, but not far from ld-lo coexistence. If an array of proteins that favored the lo phase were introduced into the system, then it is likely that they would induce a wetting transition at coexistence. In fact, before the miscibility critical point is reached along coexistence, such a transition has to occur according to Cahn's well-known argument (22,23). Off of coexistence, there would be a region of lo-like fluid surrounding any such protein. This is a region in which the radius would be finite, because the system is off of coexistence (so that the lo phase is not thermodynamically stable), and because the proteins are not in an array (24) (i.e., they occur as monomers or in small clusters). There are also dynamic models of raft formation (25) that, biologically, take recycling and diffusion into account.

Given this controversy on the nature and existence of rafts, it would be very useful to calculate the partition coefficient within the phase separation hypothesis and a model system, and to determine its variation with the architecture of the anchor. To do so, of course, requires not only a reasonable description of the anchors, but also a model that produces coexisting liquid-ordered and liquid-disordered phases. Such a model would be comprised of a minimum of three components: saturated lipids, unsaturated lipids, and cholesterol. We have carried out such a program. The partition coefficients are calculated as a function of chain length, degree of saturation, and temperature. Perhaps our most important observation is model-independent: that the partitioning depends strongly on the lipid environment in which the anchors come into contact, and therefore the partition coefficient depends not only on the nature of the anchor, but, for a given anchor, must also depend on the overall composition of the system. This composition determines the difference in concentrations of the components in the coexisting lo and ld phases. Such differences can be infinitesimal, such as at a critical point (21,26). In this case, the partition coefficient must be unity, or the differences between lo and ld phases can be large (in which case, the partition coefficient may differ substantially from unity).

From our theoretical model-membrane system, we report calculated partition coefficients for single chains of various lengths and saturation and for a few cases of double-chained molecules. The results reproduce the observations that partition coefficients increase with chain length and degree of saturation. They also predict that variation of the length of the anchors, which are short compared with those making up the bilayer, has little effect on the partition coefficient, and that double bonds located near the ends of chains have less effect than those near the middle.

Model Ternary System

We consider a fluid, planar, symmetric lipid bilayer of thickness L. This is composed of a ternary system of cholesterol, a lipid with two saturated hydrocarbon chains of 16 carbons, C16:0, such as dipalmitoylphosphatidylcholine (DPPC), and a lipid with two monounsaturated hydrocarbon chains of 18 carbons, C18:1, such as dioleoylphosphatidylcholine (DOPC). The chains are described by Flory's Rotational Isomeric States Model (27,28) in which each CH₂ group is in one of three configurations: the lowest energy trans, or the gauche-plus or the gauche-minus (both of which are of an energy, 500 cal/mol, greater than that of the trans configuration). These states are thermally populated. There are N molecules of which a fraction, x_c, is cholesterol; x_s, saturated lipid; and x_u, unsaturated lipid. When necessary, we indicate molecules in the inner leaflet by a subscript (in) and those in the outer leaflet by (o). We treat separately the contributions to the free energy arising from the lipid hydrocarbon chains and from the polar headgroups. From our mean-field theory, we write the total free energy per molecule, f ≡ F/N, in the form of a sum of the two intralayer free energies and a coupling between them,

$$\beta f\left(T,a,x_{\text{s}},x_{\text{u}},x_{\text{c}}\right)=\sum _{\delta =\text{in},\text{o}}\beta f_{\delta }+\beta f_{\text{coupl}},$$ (1)

where β = 1/k_BT. The intralayer free energies arise from the interaction of the chains with the polar headgroups and external water; from the entropy of mixing of the three components; from the free energy arising simply from the many different configurations of the single chains; and from an interaction between chains in the same leaf. These four contributions are written

$$\beta f_{\delta }\equiv \beta {\gamma }_{0}a+\sum _{\text{i}=\text{s},\text{u},\text{c}}\frac{x_{\text{i}}}{2}\ln \left(x_{\text{i}}{\lambda }_{\text{i}}^2/a\right)+\beta f_{\text{config},\delta }+\beta f_{\text{orient},\delta },$$ (2)

where γ₀ is the water-hydrocarbon interfacial free energy, and a is the molar area of the midplane of the bilayer, the total volume of the bilayer divided by its thickness L:

$$a\left(x_{\text{s}},x_{\text{u}},x_{\text{c}},L\right)=\frac{2x_{\text{s}}{\nu }_{\text{s}}\left(n_{\text{s}}+1\right)+2x_{\text{u}}\left(\left(n_{\text{u}}-1\right){\nu }_{\text{s}}+2{\nu }_{\text{CH}}\right)+x_{\text{c}}{n}_{\text{c}}{\nu }_{\text{c}}}{L}\text{.}$$

Here ν_s, ν_CH, and ν_c are the volumes of a CH₂ unit, of half a –CH = CH– unit, and of each carbon unit in cholesterol. The thermal wavelength of the i^th component is denoted λ_i.

The configurational free energy of the chains is

$$\beta f_{\text{config},\delta }\equiv \sum _{\text{i}}\frac{x_{\text{i}}}{2}{n}_{\text{i}}^{\text{tails}}\sum _{{\alpha }_{\text{i},\delta }}{P}_{\text{i},\delta }\left({\alpha }_{\text{i},\delta }\right)\left(\ln P_{\text{i},\delta }\left({\alpha }_{\text{i},\delta }\right)+\beta \epsilon \left({\alpha }_{\text{i},\delta }\right)\right),$$ (3)

where $n_{\text{i}}^{\text{tails}}$ is the number of tails of species i; i.e.,

$$n_{\text{s}}^{\text{tails}}=n_{\text{u}}^{\text{tails}}=2,n_{\text{c}}^{\text{tails}}=1\text{.}$$

Further P(α_{j, δ}) is the probability of finding the chain of molecular species j in leaf δ in a particular conformation specified by the index α_{j, δ}, one with a total internal energy ε(α_{j, δ}). The internal energy arises from the gauche bonds whose energies exceed that of the trans configuration.

The orientational interaction between chains i and j in the same leaf is written

$$\beta f_{\text{orient},\delta }\equiv -\sum _{\text{i}}\sum _{\text{j}}\beta J_{\text{i},\text{j}}\frac{x_{\text{i}}}{2}\frac{x_{\text{j}}}{2}\frac{n_{\text{i}}^{\text{tails}}{n}_{\text{j}}^{\text{tails}}}{2a{\nu }_{\text{s}}}\int \langle {\xi }_{\text{i},\delta }\left(z\right)\rangle \langle {\xi }_{\text{j},\delta }\left(z\right)\rangle dz,$$ (4)

where 〈ξ_{i, δ}(z)〉 is the ensemble average of the local density of bonds weighted by their relative orientation to the bilayer normal.

The explicit coupling of the chains from the two different leaves is due to the interaction between chains that overlap near the midplane. It is of the same form as the interaction between chains within the same leaf,

$$\beta f_{\text{coupl}}=-\sum _{\text{i}}\sum _{\text{j}}\beta J_{\text{i},\text{j}}\frac{x_{\text{i}}}{2}\frac{x_{\text{j}}}{2}\frac{n_{\text{i}}^{\text{tails}}{n}_{\text{j}}^{\text{tails}}}{a{\nu }_{\text{s}}}\int \langle {\xi }_{\text{i},\text{o}}\left(z\right)\rangle \langle {\xi }_{\text{j},\text{in}}\left(z\right)\rangle dz\text{.}$$ (5)

In sum, the free energy of the system is given by Eqs. 1–5.

The two leaves are not only coupled explicitly by this interaction but also implicitly by the fact that these overlapping chains each contribute to the volume of the hydrophobic region, a region whose density we constrain to be constant (i.e., that it be incompressible). The constant density implies

$$adz=\sum _{\text{i},\delta }\frac{x_{\text{i}}}{2}{n}_{\text{i}}^{\text{tails}}\langle {\nu }_{\text{i},\delta }\left(z\right)\rangle dz$$ (6)

for 0 < z < L, where 〈ν_{i, δ}(z)〉 is the ensemble-averaged contribution to the volume of the hydrophobic core at z from the molecules of species i in the leaf δ. The constraint is imposed by means of a local Lagrange multiplier, π(z), which appears in the probability functions P(α_i). They have the same form for all of the components,

$$P\left({\alpha }_{\text{i}}\right)=\frac{1}{q_{\text{i}}}\exp \left[-\beta \epsilon \left({\alpha }_{\text{i}}\right)-\int \beta \pi \left(z\right){\nu }_{\text{i}}\left({\alpha }_{\text{i}},z\right)dz-\int \beta b_{\text{i}}\left(z\right){\xi }_{\text{i}}\left({\alpha }_{\text{i}},z\right)dz\right],$$ (7)

where q_i is the conformational part of the partition function of a single chain of component i

$$q_{\text{i}}=\sum _{{\alpha }_{\text{i}}}\exp \left[-\beta \epsilon \left({\alpha }_{\text{i}}\right)-\int \beta \pi \left(z\right){\nu }_{\text{i}}\left({\alpha }_{\text{i}},z\right)dz-\int \beta b_{\text{i}}\left(z\right){\xi }_{\text{i}}\left({\alpha }_{\text{i}},z\right)dz\right]\text{.}$$ (8)

The mean-fields βb_i(z) act upon the orientation of a molecule of species i at the coordinate z and result from the average orientational interactions arising from the other molecules. They are determined by the equations

$$\beta b_{\text{l}}\left(z\right)dz=-\frac{\beta J_{\text{ll}}{x}_{\text{s}}}{a{\nu }_{\text{s}}}\left(\langle {\xi }_{\text{s},\text{o}}\left(z\right)\rangle +\langle {\xi }_{\text{s},\text{i}}\left(z\right)\rangle \right)dz-\frac{\beta J_{\text{ll}}{x}_{\text{u}}}{a{\nu }_{\text{s}}}\left(\langle {\xi }_{\text{u},\text{o}}\left(z\right)\rangle +\langle {\xi }_{\text{u},\text{i}}\left(z\right)\rangle \right)dz-\frac{\beta J_{\text{lc}}{x}_{\text{c}}}{2a{\nu }_{\text{s}}}\left(\langle {\xi }_{\text{c},\text{o}}\left(z\right)\rangle +\langle {\xi }_{\text{c},\text{i}}\left(z\right)\rangle \right)dz\text{.}$$ (9)

The fields acting on saturated or unsaturated lipids are identical,

$$\beta b_{\text{s}}\left(z\right)dz=\beta b_{\text{u}}\left(z\right)dz\equiv \beta b_{\text{l}}\left(z\right)dz,$$

whereas the field acting on the cholesterol orientation is distinct and is given by

$$\beta b_{\text{c}}\left(z\right)dz=-\frac{\beta J_{\text{lc}}{x}_{\text{s}}}{a{\nu }_{\text{s}}}\left(\langle {\xi }_{\text{s},\text{o}}\left(z\right)\rangle +\langle {\xi }_{\text{s},\text{i}}\left(z\right)\rangle \right)dz-\frac{\beta J_{\text{lc}}{x}_{\text{u}}}{a{\nu }_{\text{s}}}\left(\langle {\xi }_{\text{u},\text{o}}\left(z\right)\rangle +\langle {\xi }_{\text{u},\text{i}}\left(z\right)\rangle \right)dz-\frac{\beta J_{\text{cc}}{x}_{\text{c}}}{2a{\nu }_{\text{s}}}\left(\langle {\xi }_{\text{c},\text{o}}\left(z\right)\rangle +\langle {\xi }_{\text{c},\text{i}}\left(z\right)\rangle \right)dz\text{.}$$ (10)

Equations 6, 9, and 10 comprise the set of self-consistent equations whose solution yields the equilibrium values of the fields π(z), b_l(z), and b_c(z) from which all densities, and the free energy follows. Further details of the model and its solution can be found in Appendix A.

The model produces a phase diagram that exhibits three phases: one rich in cholesterol and saturated lipids, which we identify with the liquid-ordered (lo) phase; one rich in unsaturated lipids, which we identify with the liquid-disordered (ld) phase; and one consisting almost entirely of saturated lipids, the gel phase. The phase diagram at 290 Kelvin (K) is shown in Fig. 1. This figure, along with Fig. 2 of Elliott et al. (29), is in good qualitative agreement with the experimental phase diagrams for the DPPC, DOPC, and cholesterol mixture presented in Davis et al. (16), and with the PSM, DOPC, and cholesterol mixture determined by de Almeida et al. (30). Marsh (6) presents several other experimental, three-component phase diagrams of the general form that we see in this work. Examples of such systems presented in Marsh (6) are PSM, POPC, and cholesterol along with DPPC, POPC, and cholesterol, and DSPC, SOPC, and cholesterol.

Figure 1.

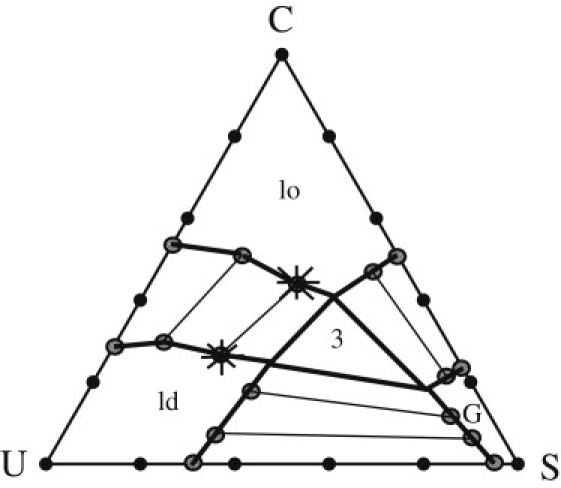
The phase diagram of the DPPC (S), DOPC (U), and cholesterol (C), lipid bilayer at 290 K as obtained from our model. The region of the gel phase is denoted G, that of the liquid-ordered phase is denoted lo, and the liquid-disordered phase, ld. Bold lines represent the phase boundaries. Tie lines connect points at compositions in coexistence with one another. The stars represent the location where the calculations for the partition coefficient took place for T = 290 K. The region of three-phase coexistence is denoted 3. Parameters are J_ll = 3.1 × 10⁻³k_BT^∗(T^∗ = 315 K), J_lc = 0.85 J_ll, and J_cc = 0.80 J_ll.

Figure 2.

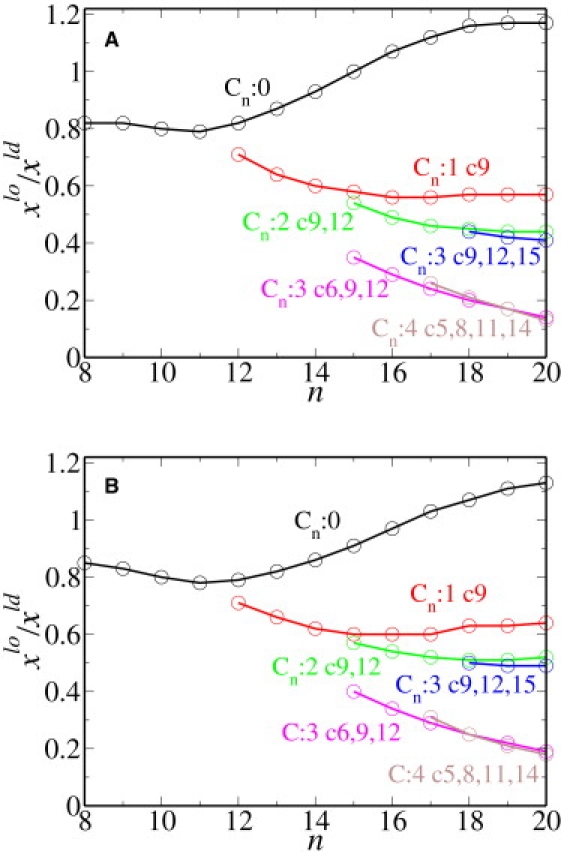
Partition coefficient for various single anchor chains embedded in a membrane consisting of model DPPC, DOPC, and cholesterol. The mole fractions of the chain anchors in the liquid-order and liquid-disorder phases are x^lo and x^ld, respectively. The number of carbons in the chain is n. (A) The temperature is 290 K. The concentrations of the lo phase are x_c = 0.48, x_s = 0.30, and x_u = 0.22, whereas those of the ld phase are x_c = 0.27, x_s = 0.21, and x_u = 0.52. (B) The temperature is 300 K. The concentrations of the lo phase are x_c = 0.52, x_s = 0.26, and x_u = 0.22, whereas those of the ld phase are x_c = 0.32, x_s = 0.22, and x_u = 0.46.

The Partition Coefficient

We now add to the ternary mixture an infinitesimal amount of a fourth component, A—an anchoring molecule whose coefficient of partition between coexisting lo and ld phases we wish to compute. The partition coefficient of this molecule between liquid-ordered and liquid-disordered phases is, by definition,

$${\kappa }_{\text{A}}=\frac{x_{\text{A}}^{\text{lo}}}{x_{\text{A}}^{\text{ld}}}\text{.}$$ (11)

The chemical potential of this molecule must be the same in the coexisting phases, and from this condition, we obtain the partition coefficient. We start by decomposing the chemical potential of the added molecule as

$$\beta {\mu }_{\text{A}}=\ln x_{\text{A}}+\beta {\tilde{\mu }}_{\text{A}},$$

where $\beta {\tilde{\mu }}_{\text{A}}$ is that part of the chemical potential that does not depend upon the concentration of the added molecule. From the equality of the chemical potential in the coexisting phases, we obtain

$${\kappa }_{\text{A}}=\frac{x_{\text{A}}^{\text{lo}}}{x_{\text{A}}^{\text{ld}}}=\exp \left(\beta {\tilde{\mu }}_{\text{A}}^{\text{ld}}-\beta {\tilde{\mu }}_{\text{A}}^{\text{lo}}\right)\text{.}$$ (12)

In Appendix B the chemical potential of an anchoring molecule, with a number of chain anchors,$n_{\text{A}}^{\text{tails}}$, is derived following the potential distribution theorem (31). It is given exactly by

$$\beta {\mu }_{\text{A}}=\ln x_{\text{A}}+\ln \left(\frac{{\lambda }_{\text{A}}^2}{2a}\right)-\ln {\sum _{\alpha }\langle \exp \left(-\beta u_{\text{A}}\right)\rangle }_{\text{N}-1},$$ (13)

where 〈…〉_N–1 represents the ensemble average of the Boltzmann factor of the anchor molecule. The average is over all the configurations of the three-component system in the absence of the anchor. The sum over α is a sum over all of the conformations of the inserted anchor molecule, u_A is the total energy of interaction experienced by the inserted chain anchor molecule, and λ_A is its de Broglie wavelength. As the ensemble average cannot be readily evaluated, we approximate it from our mean-field calculation. The expression for this chemical potential in our model is derived in Appendix B and is found to be

$$\beta {\mu }_{\text{A}}=\ln x_{\text{A}}+\beta {\tilde{\mu }}_{\text{A}},$$ (14)

$$=\ln x_{\text{A}}+\ln \left(\frac{{\lambda }_{\text{A}}^2}{2a}\right)-\ln \prod _{\text{k}=1}^{n_{\text{A}}^{\text{tails}}}{q}_{\text{k}},$$ (15)

where q_k(T, a, x_s, x_u, x_c) is the configurational part of the partition function of the chain anchors that excludes their translational degrees of freedom. Because the concentration of the anchor is infinitesimal, the partition function is independent of its concentration. From the equality of the anchor chemical potential in the coexisting phases, Eq. 12, we immediately obtain

$${\kappa }_{\text{A}}=\frac{x_{\text{A}}^{\text{lo}}}{x_{\text{A}}^{\text{ld}}}=\frac{a^{\text{lo}}\prod _{k=1}^{n_{\text{A}}^{\text{tails}}}{q}_{\text{k}}\left(T,a^{\text{lo}},x_{\text{s}}^{\text{lo}},x_{\text{u}}^{\text{lo}},x_{\text{c}}^{\text{lo}}\right)}{a^{\text{ld}}\prod _{\ell =1}^{n_{\text{A}}^{\text{tails}}}{q}_{\ell }\left(T,a^{\text{ld}},x_{\text{s}}^{\text{ld}},x_{\text{u}}^{\text{ld}},x_{\text{c}}^{\text{ld}}\right)},$$ (16)

where a^lo and a^ld are the area per molecule in the liquid-ordered and -disordered phases, respectively. The necessary partition functions can be calculated in a manner similar to those of the other three components. The configurational part of the partition function for a chain anchor embedded in the outer leaf of a membrane in the ld phase is

$$q_{\text{A}}\left(T,a^{\text{ld}},x_{\text{s}}^{\text{ld}},x_{\text{u}}^{\text{ld}},x_{\text{c}}^{\text{ld}}\right)=\sum _{{\alpha }_{\text{A},\text{o}}}\exp \left\{-\beta \epsilon \left({\alpha }_{\text{A},\text{o}}\right)-\beta \int \left[{\pi }^{\text{ld}}\left(z\right){\nu }_{\text{A}}\left({\alpha }_{\text{A},\text{o}},z\right)+b_{\text{l}}^{\text{ld}}\left(z\right){\xi }_{\text{A},\text{o}}\left({\alpha }_{\text{A},\text{o}},z\right)\right]dz\right\},$$ (17)

where the fields $\beta {\pi }^{\text{ld}}\left(z\right)$ and $\beta b_1^{\text{ld}}\left(z\right)$ are known from the ternary system and do not have to be recalculated. A similar expression obtains for a chain embedded in the coexisting lo phase.

Because the partition functions depend upon the concentrations in the coexisting phases, it is clear from Eq. 16 that the partition coefficient must also depend upon these concentrations. In fact, there are some limiting behaviors that one can determine without further calculation. The most simple behavior obtains when the system approaches a critical point. Because the difference in the lipid compositions of the coexisting phases vanishes as the critical point is approached, the partition coefficient must approach unity there.

As a second example, suppose that the ternary system phase separates into lo and ld phases with saturated lipid concentrations $x_{\text{s}}^{\text{lo}}$, and $x_{\text{s}}^{\text{ld}}$. If one were to add an identical two-tailed saturated lipid to this system, its partition coefficient would obviously be given by $\kappa =x_{\text{s}}^{\text{lo}}/x_{\text{s}}^{\text{ld}}$. If we consider an anchor with these same two tails, then to the extent that its partition coefficient is dominated by the hydrocarbon tails, we expect its partition coefficient to be the same. Further, in a homologous series of saturated, two-tailed anchors (di C_m:0) with the two-tailed saturated lipids of the membrane being characterized by the integer m_mem, we not only expect the partition coefficient κ_A(m) to take the value $x_{\text{s}}^{\text{lo}}/x_{\text{s}}^{\text{ld}}$ for m = m_mem but also to approach this value smoothly as m approaches m_mem. Because the coexisting concentrations of lipids depend upon the overall concentration of the system, the partition coefficient of this anchor must also depend upon the overall composition of the system, and not just on the components of which it is comprised.

A further result, valid within mean-field theory, can be derived concerning the effectiveness of multiple anchors compared to a single anchor; that is, the relation between the partition coefficient of an anchor with multiple chains as compared to an anchor with a single chain. From Eq. 16, one finds easily that

$${\kappa }_{\text{A}}\left(n_{\text{A}}^{\text{chains}}\right)={\left[\frac{a^{\text{ld}}}{a^{\text{lo}}}\right]}^{\left(n_{\text{A}}^{\text{chains}}-1\right)}{\left[{\kappa }_{\text{A}}\left(1\right)\right]}^{n_{\text{A}}^{\text{chains}}},$$ (18)

which shows how much more effective a multichain anchor can be in effecting a large partition of protein.

Lastly, within the same mean-field approach, one also finds that the partition coefficient of an anchor with two different chains, say a saturated one and an unsaturated one, κ_su, is related to the partition coefficients of anchors with two of the saturated chains, κ_ss and two of the unsaturated chains, κ_uu, according to

$${\kappa }_{\text{su}}={\left[{\kappa }_{\text{ss}}{\kappa }_{\text{uu}}\right]}^{1/2}\text{.}$$ (19)

We treat the anchors on the same level of approximation as the lipids in the lipid bilayer. The exact chemical architecture of the linkers in the anchor is not taken into account explicitly, just as the glycerol carbon backbone is not taken into account explicitly within our models of DPPC and DOPC. The lipid bilayer and the anchor chains are ultimately taken to be independent, and the field variables are solved for in a mean-field manner so that everything is treated within the same level of approximation. It is also important to note that we assume that the partitioning of molecules that have these lipid anchors is dominated by the partitioning of the lipid anchors themselves. We only treat the chains of the lipids explicitly, and we treat the absorbing molecules at the exact same level of approximation. We could consider the entire adsorbing molecule along with the headgroups of the lipids explicitly in this theory; however, that is currently beyond the scope of this work.

As can be seen from our derivation of the partition coefficient in Appendix B, we perform these calculations in the infinite-dilution limit, and therefore the chains of the anchor have no effect on the structure of the equilibrium lipid bilayer. Were one interested in the effects of a large concentration of anchors, one would have to consider a mixture of four components by means of a straightforward, but tedious, extension of the calculation presented here. Given the agreement found with experiments, we believe that infinite dilution is a good approximation.

Results and Discussion

We have calculated the partition coefficients of various anchors between lo and ld phases that are in coexistence with one another at a temperature of T = 290 K and of T = 300 K. We first focus on the results for T = 290 K. We choose a coexistence of lo phase characterized by an area per molecule of 46.28 Ų and an ld phase characterized by 59.20 Ų. The concentrations of the lo phase are x_c = 0.48, x_s = 0.30, and x_u = 0.22, whereas those of the ld phase are x_c = 0.27, x_s = 0.21, and x_u = 0.52. The partition coefficients for several single-chain anchors are shown in Fig. 2 A as a function of the chain length n. The notation C_m: k cp₁, …, p_k indicates a C_m chain that contains k cis double bonds. The positions of the double bonds in the C_m chain are given by p₁, …p_k, where p_j indicates that there is a double bond between C_p and C_p+1. Thus C_m: 2 c9, 12 is a double-unsaturated chain with cis double bonds between C9 and C10 and between C12 and C13. Examples of the molecules with chains described in Fig. 2 are (from top to bottom, starting on the black curve) myristic acid, C₁₄:0, and stearic acid C₁₈:0; (on the red curve) oleic acid C₁₈:1 c9 and palmitoleic acid C₁₆:1 c9; (on the green curve) linoleic acid C₁₈:2 c9, 12; (on the blue curve) α-linoleic acid C₁₈:3 c9, 12, and 15; (on the magenta curve) γ-linolenic acid C₁₈:3 c6, 9, and 12; and (on the brown curve) arachidonic acid C₁₈:4 c5, 8, 11, and 14.

We note that several trends observed in experiment (9,32,33) are reproduced here. In particular, the partition coefficients for the saturated anchors increase with the length of the anchor chain provided only that the chains are longer than 11 carbons. The rate of increase is not uniform. Indeed, we observe that saturated chains of length 18 and 20 partition equally, just as observed in experiment (9). We find that the partition coefficient increases with increasing degree of saturation, again in agreement with experiment (9). One also notes from a comparison of the results for C_m:3 c9, 12, and 15 and C_m:3 c6, 9, and 12 that the location of the double bonds affects the partition coefficient. In particular, it is larger if the double bonds are nearer the ends of the chain. Presumably, this is because the order parameter, even of the saturated chains comprising much of the bilayer, decreases toward the end of the chains. Thus, double bonds of the anchor disturb the lo phase less when they are close to the chain ends.

We have also calculated partition coefficients for three classes of double-tailed anchors: those with two saturated chains, di-C_m:0; those with one saturated and one monounsaturated chain, C_m:0 − C_m:1 c9; and those with two monounsaturated chains, di-C_m:1 c9. The results are shown in Fig. 3 A. As expected, the partition coefficient of the diunsaturated chains is least; that of the mixed chains is larger, and that of the disaturated chains is largest. We note, however, that the differences are small. The value of the partition coefficient of di-C₁₆:0 is 1.43 and is shown by a star in the figure. This value corresponds to the partition coefficient of DPPC in the equilibrium bilayer which, from the concentrations given above, is $x_{\text{s}}^{\text{lo}}/x_{\text{s}}^{\text{ld}}=0.30:0.21=1.43$. The agreement is to be expected, as stated earlier and shown explicitly in Appendix B. The value of the partition coefficient of di-C₁8:1 c9 is 0.42, also shown by a star in the figure, and corresponds to the partition coefficient of DOPC in the equilibrium bilayer, $x_{\text{u}}^{\text{lo}}/x_{\text{u}}^{\text{ld}}=0.22:0.52=0.42$.

Figure 3.

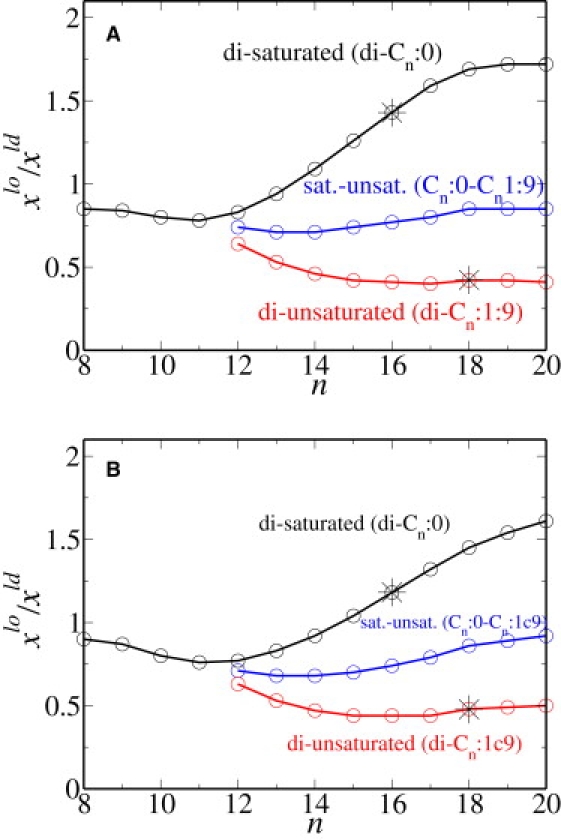
Partition coefficient for various double-chain anchors embedded in a membrane consisting of model DPPC, DOPC, and cholesterol. The mole fractions of the chain anchors in the liquid-order and liquid-disorder phases are x^lo and x^ld, respectively. The number of carbons in the chain is n. The stars represent the values of the partition coefficient in the bulk lipid bilayer. (A) The temperature is 290 K. The concentrations of the lo phase are x_c = 0.48, x_s = 0.30, and x_u = 0.22, whereas those of the ld phase are x_c = 0.27, x_s = 0.21, and x_u = 0.52. (B) The temperature is 300 K. The concentrations of the lo phase are x_c = 0.52, x_s = 0.26, and x_u = 0.22, whereas those of the ld phase are x_c = 0.32, x_s = 0.22, and x_u = 0.46.

To study the effect of temperature on the partition coefficient, we repeat our calculations for a temperature of T = 300 K. We choose a coexistence at which the lo phase has an area per molecule of 47.0 Ų, and concentrations of x_c = 0.52, x_s = 0.26, and x_u = 0.22, whereas the ld phase has the larger area per molecule of 59.90 Ų, and concentrations x_c = 0.32, x_s = 0.22, and x_u = 0.46. These concentrations are close, but not identical, to those at the lower temperature. The results for the single chain anchors are presented in Fig. 2 B and those for the double tails are presented in Fig. 3 B. The value of the partition coefficient of DPPC at this temperature is 1.18. The fact that the partition coefficient of DPPC decreases with increasing temperature for saturated chains >12 carbons is to be expected from our observation that the coefficients are directly related to the concentrations of the components of the membrane, and that the difference in concentrations between coexisting phases decreases with increasing temperature for long saturated chains. Indeed, our result is consistent with the experimental results of Davis et al. (16), as shown in their Fig. 11. The effect on the partition coefficient both of temperature and of multiple anchors on the partition coefficient is shown in Fig. 4. The effect of temperature on the partition coefficient is dependent on the length of the saturated chains relative to those that are a major component of the bilayer itself. According to Fig. 4, the partitioning into the lo phase of saturated chains longer than 11 carbons increases with decreasing temperature, indicating that energetic considerations dominate entropic ones. However, for saturated chains shorter than 10 carbons, this partitioning increases with increasing temperature, indicating that entropic considerations are dominant. This is in accord with the work of deGennes (34) on the chain-length dependence of the adsorption of one polymer into a layer of another. Temperature has very little effect on the partitioning of unsaturated chains as can be seen from a comparison of Fig. 2, A and B, for single chain anchors and Fig. 3, A and B, for double tail anchors.

Figure 4.

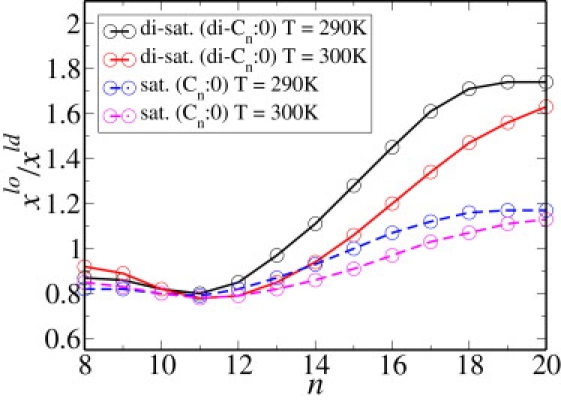
Partition coefficient for various saturated chain anchors embedded in a membrane consisting of model DPPC, DOPC, and cholesterol. The temperatures are 290 K and 300 K.

Another commonly studied double-chain anchor motif that we have considered is C 18:0–C₂₀:4c 5, 8, 11, and 14, which corresponds to a GPI-anchored protein. At a temperature of T = 300, we obtain a partition coefficient of 0.24. The experimental results for this anchor are that ∼20–30% associate with the liquid-order phase (12). To compare our partition coefficient value with this number, we have to take into account that the partition coefficient gives the mol fraction of the chain anchors in the lo phase relative to the mol fraction of the chain anchors in the ld phase, not the fraction of the total amount of the chain anchors in one phase. However, a simple calculation shows that the fraction of anchor in the lo phase, f_A, is related to the partition coefficient by

$$f_{\text{A}}=\frac{N_{\text{A}}^{\text{lo}}}{N_{\text{A}}^{\text{lo}}+N_{\text{A}}^{\text{ld}}}=\frac{{\kappa }_{\text{A}}\left({\mathcal{A}}^{\text{lo}}/{\mathcal{A}}^{\text{ld}}\right)\left(a^{\text{ld}}/a^{\text{lo}}\right)}{1+{\kappa }_{\text{A}}\left({\mathcal{A}}^{\text{lo}}/{\mathcal{A}}^{\text{ld}}\right)\left(a^{\text{ld}}/a^{\text{lo}}\right)},$$ (20)

where ${\mathcal{A}}^{\text{lo}}/{\mathcal{A}}^{\text{ld}}$ is the ratio of the extensive areas of the lo and ld phases. This ratio depends upon the average composition of the system and the phase diagram according to the usual lever rule. If we take the extensive area of the lo phase to be equal to that of the ld phase, we find that 23% of this chain anchor molecule associates with the lo phase, which is well within the experimental range. The 20–30% value obtained in Kahya et al. (12) is for the human placental alkaline phosphatase (PLAP) GPI-anchored protein. PLAP has been extensively reported as a membrane protein with a very high affinity for the lo phase (>95%, according to (17)). This conclusion was mainly drawn from detergent-resistant membrane components and the assumption that lo domains and their associated proteins existing in the model membranes at 37°C preserve their compositions under cold-detergent extraction (17). However, it has been shown via both experiment and theory that this assumption is not valid (35). In contrast, the experiment of Kahya et al. (12) uses florescence microscopy to study the intact membrane of domain-forming giant unilamellar vesicles and this provides a much more reliable measure of the partitioning of PLAP. With the use of this same technique, another GPI-anchored protein, Thy-1, was shown to partition into the lo phase by at most 40% (36). This result indicates that our calculations of the partition coefficient are in the experimental range for a variety of different proteins that are attached to the membrane by the same anchoring motif. This suggests that exploration of the partitioning of lipid anchors themselves is a good model for the partitioning of proteins that use these lipids to attach to the membrane.

Conclusions

We have presented the first microscopic model calculation of the extent to which various common anchors partition themselves between liquid-ordered and liquid-disordered phases. The partition coefficients are calculated as a function of chain length, degree of saturation, and temperature. We find excellent qualitative agreement between theory and experiment: i.e., that the partitioning into the lo phase is the least for highly unsaturated chains and increases as the degree of saturation increases; that the partitioning of saturated chains increases with their length provided their length is comparable with the chains of the bilayer; and that the partitioning of saturated chains into the liquid-ordered phase increases with decreasing temperature, but that the temperature has little effect on the absolute values of the partition coefficient for the shorter saturated chains. We found that the partitioning of short chains increases with increasing temperature, indicating that their partitioning, in contrast to that of longer chains, is dominated by entropic effects. We also found that for unsaturated anchors, the partition coefficient depends on the location of the double bonds. Unsaturated anchors with double bonds near the chain ends cause a smaller decrease in the fraction of anchors in the liquid-ordered phase than anchors with double bonds closer to the middle of the anchor.

We are also able to predict how the partition coefficient varies as the number of saturated or unsaturated chains in the anchor increases. The effect of doubling the number of saturated chains in an anchor is to increase the partitioning into the liquid-ordered phase when the tails are nearly as long or longer than those comprising the bilayer, but the effect of doubling the number of saturated tails is minimal when they are relatively short. Doubling the number of chains and reducing the temperature has essentially no effect on the partitioning of unsaturated chains. Lastly, we find that the partitioning depends on the difference between the lipid environments of the coexisting phases in which the anchors are embedded. Consequently, the partition coefficient depends not only upon the lipid components and the nature of the anchor, but also upon the relative compositions of the coexisting phases.

Appendix A: The Model

Because the model has been presented and explored previously (29), our description here can be brief. The volume of the monomer unit CH₂ is taken to be ν_s = 27 ų, and that of a CH₃ group is 54 ų. Each half of the –CH=CH– segment of the cis-unsaturated bond is assigned a volume of ν_CH = 0.8ν_s. The number of carbons in each saturated chain is n_s = 16, whereas the number of carbons in each unsaturated chain is n_u = 18. The local orientation of the chain is conveniently specified by the unit normal to the plane determined by the k^th CH₂ group,

$${\mathbf{u}}_{\sigma ,\mathrm{k}}=\delta {\mathbf{r}}_{\text{k}}/\left|\delta {\mathbf{r}}_{\text{k}}\right|,\delta {\mathbf{r}}_{\text{k}}\equiv {\mathbf{r}}_{\text{k}-1}-{\mathbf{r}}_{\text{k}+1},$$

with k = 1, .…n_s − 1. Just as for the lipids, the configuration of the cholesterol is completely specified by the location of all of its carbon atoms and of the angles between them. The orientation of the small acyl chain of the cholesterol is specified in the same manner as for the lipid chains. The orientation of its rigid rings are specified by the unit vector, u_c, from the 3rd to the 17th carbon in the molecule, using the conventional labeling, and a normal vector to the plane of those rings. The number of carbons in cholesterol is n_c = 27, and the volume of the carbons is ν_c = 21.0 ų.

Because the orientational interaction between bonds depends upon the local orientation of these bonds with respect to the bilayer normal, c, it is convenient to introduce a function, ξ_σ(α, z), that measures the local density of bonds weighted by their orientation with respect to the bilayer normal (37),

$${\xi }_{\text{i}}\left(\alpha ,z\right)dz=\sum _{\text{k}=1}^{n_{\text{i}}-1}{\nu }_{\text{i},\text{k}}\left(\alpha ,z\right)g\left({\mathbf{u}}_{\text{k}}·\mathbf{c}\right)dz,$$ (21)

where ν_{i, k}(α, z)dz is the volume that segment k in molecule i has in conformation α at position z. The function g is chosen to be

$$g\left(\mathbf{u}·\mathbf{c}\right)=\left(m+1/2\right){\left(\mathbf{u}·\mathbf{c}\right)}^{2\text{m}}\text{.}$$

For large m, g ≈ m exp(–mθ²), where θ is the angle between the two unit vectors. Matching lipid parameters, we have taken m = 18.

We take the strengths of the local interactions between bonds in lipid tails to be the same irrespective of whether the bonds are in a saturated or unsaturated chain: J_ss = J_uu = J_su ≡ J_ll. Thus, the difference in free energy between saturated and unsaturated lipids arises solely from the fact that the configurations of these lipids differ due to the presence of the double bond in the unsaturated lipids, not to any explicit difference in interaction energies.

To evaluate the single-molecule partition functions, q_i (Eq. 8), we generate ∼10⁸ configurations of each molecule. We then search the composition space at a given temperature for phase coexistence. Phase equilibria is determined by standard thermodynamic equalities (38): that the chemical potentials of the three components be equal in each phase; that the surface tensions be equal in each phase; and that the common value of the surface tension be zero. The strength of the interaction between chain segments, J_ll, is set such that the calculated main-chain transition temperature of a lipid with two saturated tails of 16 carbons, C16:0, is equal to that of dipalmitoylphosphatidylcholine (DPPC), T = 315 K. This determines that

$$J_{\text{ll}}=3.1\times {10}^{-3}{k}_{\mathrm{B}}{T}^{\ast }\left(T^{\ast }=315\text{k}\right)\text{.}$$

To obtain the best qualitative fit of our phase diagram to those of experiment, we have chosen

$$J_{\text{lc}}=0.85J_{\text{ll}}\text{and}{J}_{\text{cc}}=0.80J_{\text{ll}}\text{.}$$

For a temperature T = 290 K we obtain the phase diagram shown in Fig. 1.

When we choose T = 300, we obtain a phase diagram very similar to that shown in Fig. 2 of Elliott et al. (29) for that temperature. Our parameters differ from those of Elliott et al. (29) because we have included the translational entropy in the free energy, and because we employ an order-of-magnitude more configurations for each molecule. Fig. 2 of Elliott et al. (29) also includes a plot of the order parameters of the saturated tails in the three phases, lo, ld, and gel, which coexist at the triple point.

Appendix B: Chemical Potential

The chemical potentials of the three components that comprise the bilayer can be calculated by taking the appropriate derivative of the free energy with respect to the number of molecules,

$${\mu }_{\text{i}}={\left(\frac{\partial F_{\text{mft}}}{\partial N_{\text{i}}}\right)}_{\text{T},\mathcal{A},\text{N}\left[\text{i}\right]},$$ (22)

where N[i] means that all of the species except species i are held fixed and A is the area of the bilayer. Because the two leaves are identical, there is no difference between the chemical potentials of species i in either leaf irrespective of whether the species can interchange between the two leaves. The expression for the free energy within mean-field theory,

$$F_{\text{mft}}\left(T,N_{\text{s}},N_{\text{u}},N_{\text{c}},\mathcal{A}\right),$$

is obtained by substituting the probability distribution functions (Eq. 7) into the free energy (Eq. 1) and including the incompressibility constraint. We find that all chemical potentials can be written in the form

$$\beta {\mu }_{\text{j}}=\ln \left(\frac{x_{\text{j}}{\lambda }_{\text{j}}^2}{2a}\right)-n_{\text{j}}^{\text{tails}}\ln q_{\text{j}},j=\text{s},\text{u},\text{c}\text{.}$$ (23)

In particular, the chemical potential of the two-tailed, saturated lipid component of the membrane is

$$\beta {\mu }_{\text{s}}=\ln \left(\frac{x_{\text{s}}{\lambda }_{\text{s}}^2}{2a{q}_{\text{s}}^2}\right)\text{.}$$ (24)

We now turn to the determination of the chemical potential of the anchors. There are several ways that it can be determined, and we choose to follow the method of Widom's (31) potential distribution theorem. We begin with the expression of the chemical potential of anchor A as

$$\beta {\mu }_{\text{A}}=-\ln \left[\frac{Q_{\text{N}}}{Q_{\text{N}-1}}\right],$$ (25)

where Q_N is the partition function of the four-component system of N molecules with molecules 1 to N_s corresponding to the saturated lipids, N_s + 1 to N_s + N_u to the unsaturated lipid, N_s + N_u + 1 to N_s + N_u + N_c = N − 1 to the cholesterol molecules, and the final N^th molecule is the chain anchor molecule (molecule A). Thus, the chain anchor molecule is in the limit of infinite dilution. The partition function Q_N–1 is that of the three-component system without the chain anchor and thus contains N − 1 molecules. We separate the partition functions into translational and configurational parts so that the chemical potential of anchor A is

$$\beta {\mu }_{\text{A}}=\ln \left(\frac{x_{\text{A}}{\lambda }_{\text{A}}^2}{2a}\right)-\ln \left[\frac{\int \cdots \int \exp \left(-\beta U_{\text{N}}\left({\mathbf{r}}_1,\dots ,{\mathbf{r}}_{{\nu }_{\text{N}}\text{N}}\right)\right)d{\mathbf{r}}_1\dots d{\mathbf{r}}_{{\nu }_{\text{N}}\text{N}}}{\mathcal{A}\int \cdots \int \exp \left(-\beta U_{\text{N}-1}\left({\mathbf{r}}_1,\dots ,{\mathbf{r}}_{{\nu }_{\left(\text{N}-1\right)}\left(\text{N}-1\right)}\right)\right)d{\mathbf{r}}_1\dots d{\mathbf{r}}_{{\nu }_{\left(\text{N}-1\right)}\left(\text{N}-1\right)}}\right],$$ (26)

where ν_i is the total number of degrees of freedom for the molecule (number of chain units and the degrees of freedom of the headgroup of molecule i), and the configurations of the molecules are specified by

$$\left({\mathbf{r}}_1,\dots ,{\mathbf{r}}_{{\nu }_{\left(\text{N}-1\right)}\left(\text{N}-1\right)}\right)\text{.}$$

The potential energy of the total system can be written as

$$U_{\text{N}}\left({\mathbf{r}}_1,\dots ,{\mathbf{r}}_{{\nu }_{\text{N}}\text{N}}\right)=U_{\text{N}-1}\left({\mathbf{r}}_1,\dots ,{\mathbf{r}}_{{\nu }_{\left(\text{N}-1\right)}\left(\text{N}-1\right)}\right)+u_{\text{N}}\left({\mathbf{r}}_1,\dots ,{\mathbf{r}}_{{\nu }_{\left(\text{N}-1\right)}\left(\text{N}-1\right)},{\mathbf{r}}_{\left(\text{N},\text{head}\right)},\alpha \right),$$ (27)

where

$$u_{\text{N}}\left({\mathbf{r}}_1,\dots ,{\mathbf{r}}_{{\nu }_{\left(\text{N}-1\right)}\left(\text{N}-1\right)},{\mathbf{r}}_{\left(\text{N},\text{head}\right)},\alpha \right)$$

is the total energy of interaction experienced by the N^th molecule with its headgroup at position, (r_{(N, head)}), and the chains of the N^th molecule are in conformation, α. The total energy of the three-component system without the chain anchor is U_N–1. We can now decompose the configurational part of Eq. 26 to write

$$\beta {\mu }_{\text{A}}=\ln \left(\frac{x_{\text{A}}{\lambda }_{\text{A}}^2}{2a}\right)-\ln \left[\frac{\int \exp \left(-\beta U_{\text{N}-1}\right)d{\mathbf{r}}_1\dots d{\mathbf{r}}_{{\nu }_{\left(\text{N}-1\right)}\left(\text{N}-1\right)}\int \sum _{\alpha }\exp \left(-\beta u_{\text{N}}\right)d{\mathbf{r}}_{\left(\text{N},\text{head}\right)}}{\mathcal{A}\int \exp \left(-\beta U_{\text{N}-1}\right)d{\mathbf{r}}_1\dots d{\mathbf{r}}_{{\nu }_{\left(\text{N}-1\right)}\left(\text{N}-1\right)}}\right]\text{.}$$ (28)

Because the system is homogeneous, u_N is taken to be independent of r_(N, head) so that we can integrate over r_{(N, head)} to give the area of the bilayer leaflet A. We then get the following exact relation for the chemical potential of the anchor,

$$\beta {\mu }_{\text{A}}=\ln \left(\frac{x_{\text{A}}{\lambda }_{\text{A}}^2}{2a}\right)-\ln \sum _{\alpha }{\langle \exp \left(-\beta u_{\text{N}}\right)\rangle }_{\text{N}-1},$$ (29)

where 〈…〉_N–1 is a canonical average in the (N − 1)-molecule system, in which the configurations of the N − 1 molecules are not influenced by the presence of the N^th test molecule. At this point, we can use the mean field approximation to calculate the configurational part of the chemical potential. If there are multiple chain anchors on the absorbing molecules, we assume that the chains are independent of each other. There are three contributions to u_N: one is the internal energy of the chain, the second is the contribution of the incompressibility field, βπ(z), and the third is the contribution of the alignment field, βb_l(z). We can now write the chemical potential of an anchor as

$$\beta {\mu }_{\text{A}}=\ln \left(\frac{x_{\text{A}}{\lambda }_{\text{A}}^2}{2a}\right)-\sum _{\text{k}=1}^{{\text{n}}_{\text{A}}^{\text{tails}}}\ln \sum _{{\alpha }_{\text{A}}}\exp \left\{-\beta \epsilon \left({\alpha }_{\text{A}}\right)-\beta \int \left[\pi \left(z\right){\nu }_{\text{A}}\left({\alpha }_{\text{A}},z\right)+b_{\text{l}}\left(z\right){\xi }_{\text{A}}\left({\alpha }_{\text{A}},z\right)\right]dz\right\}$$ (30)

$$=\ln \left(\frac{x_{\text{A}}{\lambda }_{\text{A}}^2}{2a}\right)-n_{\text{A}}^{\text{tails}}\ln q_{\text{A}},$$ (31)

where $n_{\text{A}}^{\text{tails}}$ is the number of chains of the anchoring molecule, and we have used Eq. 8. This is precisely the same form as the chemical potential of the components of the bilayer, Eq. 23. Because of this, it is easily seen that the partition coefficient of an anchor which is identical to either the saturated or the unsaturated component of the bilayer must be the same as the partition coefficient of that bilayer component. This stems from the fact that the partition coefficient is determined from the equality of the chemical potential in coexisting phases and from the form of the relation between chemical potential and concentration.