Skip to main content
. Author manuscript; available in PMC: 2011 May 1.
Published in final edited form as: Neuropsychologia. 2010 Feb 4;48(6):1525–1542. doi: 10.1016/j.neuropsychologia.2010.01.013

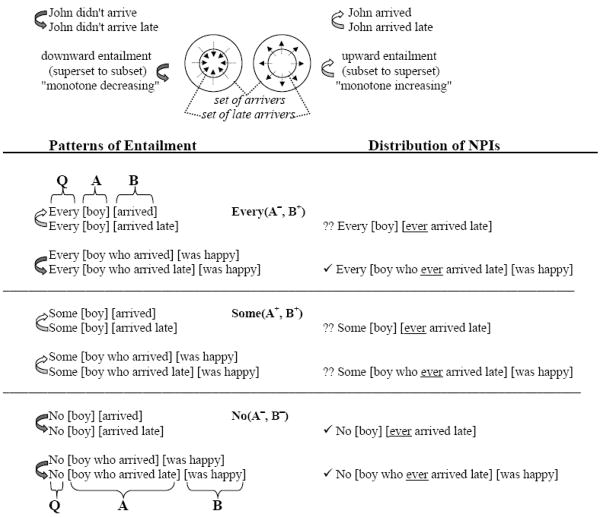
Figure 1. Monotonicity and NPI-licensing properties of EVERY, SOME, and NO.

Figure 1

We assume here a view of quantifiers as predicates of sets (see Barwise & Cooper 1981). On this view a quantifier Q takes two arguments, its “A”-argument or restriction and its “B”-argument (here: the main predicate). Thus, for example, in Every boy arrived, every is the quantifier, its restriction (A-argument) is the associated noun (boy), and the predicate arrived is “B-argument”. Satisfying the truth conditions for EVERY(A, B) would involve checking to see whether the set of entities that are boys is a subset of the set of entities that arrived (formally: EVERY(A, B) is true iff A ⊆ B). These three different quantifiers manifest different patterns of upward and downward monotonicity over each of their two arguments (illustrated by the upward and downward arrows connecting the example sentences in the left-hand panel above). Every, for example, is downward monotonic over its “A”-argument and upward monotonic over its “B”-argument (we mark this as EVERY(A−, B+), with the “−/+” marking downward/upward monotonicity, respectively), and this is evident both in the entailment patterns and in the distribution of NPIs (compare left and right panels above). In contrast, some is uniformly upward monotonic and cannot license an NPI in either position, and no is uniformly downward monotonic and uniformly licenses NPIs.