Protein structure prediction enhanced with evolutionary diversity: SPEED

Abstract

For naturally occurring proteins, similar sequence implies similar structure. Consequently, multiple sequence alignments (MSAs) often are used in template-based modeling of protein structure and have been incorporated into fragment-based assembly methods. Our previous homology-free structure prediction study introduced an algorithm that mimics the folding pathway by coupling the formation of secondary and tertiary structure. Moves in the Monte Carlo procedure involve only a change in a single pair of φ,ψ backbone dihedral angles that are obtained from a Protein Data Bank-based distribution appropriate for each amino acid, conditional on the type and conformation of the flanking residues. We improve this method by using MSAs to enrich the sampling distribution, but in a manner that does not require structural knowledge of any protein sequence (i.e., not homologous fragment insertion). In combination with other tools, including clustering and refinement, the accuracies of the predicted secondary and tertiary structures are substantially improved and a global and position-resolved measure of confidence is introduced for the accuracy of the predictions. Performance of the method in the Critical Assessment of Structure Prediction (CASP8) is discussed.

Introduction

Given the expansion of the sequence database, an imperative of the field of structural biology is to cluster related sequences into families and determine a representative structure for each family.^1–5 The already large number of families is rapidly expanding and the cost of determining representative protein structures is high. Computational structure prediction may provide the most effective means of mapping the protein universe. Structure prediction, however, is inherently challenging because of the enormous conformational space accessible to each amino acid sequence. For this reason, the most successful prediction methods seek to narrow the conformational search, for example by using large Protein Data Bank (PDB)-based fragments⁶ rather than simulating the protein ab initio.^7,8

We have recently developed a C_β-level, homology-free structure prediction algorithm, termed ItFix,⁹ in which the conformational search space is restricted by iteratively fixing secondary (2°) structure assignments of certain portions of the sequence after incorporating the influence of tertiary (3°) context. Moreover, the iterative feature enables regions of lower confidence to be predicted after the fixing of more confident regions. The coupling and mutual stabilization of 2° and 3° structure formation mimics the pathway character exhibited by real proteins.^10,11

The computationally rapid algorithm uses moves involving only the change in a single pair of φ,ψ dihedral angles (pivot moves). Hence, its performance is independent of the existence of appropriate fragments from the PDB. Nevertheless, our algorithm can outperform current homology-based 2° structure prediction methods for many proteins. ItFix also generates 3° structures of comparable accuracy to existing methods for many small proteins, including ones with few sequence homologues.

Our earlier study revealed that a large impediment to more accurate structure prediction arises from the intrinsically low propensity of some residues to adopt the backbone dihedral angles found in their native structures. In the protein 1dcj, for example, the middle of a helix contains a proline followed by a glycine, two residues that are very unlikely to be found together in helices. Even though ItFix uses more confidently assigned regions to identify native structure in otherwise weakly determined regions, the additional contextual information occasionally is insufficient to override very strong local biases. Unfortunately, issues of this severity occur often in many proteins, and the associated errors can detrimentally affect the accuracy of the 2° and 3° structure prediction.

Here, we employ multiple sequence alignments (MSAs) to mitigate the influence of the nonnative local biases. MSAs are incorporated into many popular 2° structure^12,13 and both template-based^14–16 and template-free^17,18 3° structure prediction methods. In our distribution of sampled φ,ψ angles, the nonnative biases are manifested as a low probability of native-like angles. This PDB-based distribution is now enriched using the sequence diversity found in an MSA, but does without requiring structural information from any constituent sequence. We denote this procedure as Structure Prediction Enhanced by Evolutionary Diversity (SPEED; Fig. 1). The combination of ItFix and SPEED significantly increases the accuracy of 2° and 3° structure predictions, and more so in combination with novel energy functions and clustering methods. We also provide global and local measures of the confidence of our predictions, thereby providing an essential tool for assessing the accuracy of the predicted structures of unsolved sequence families.

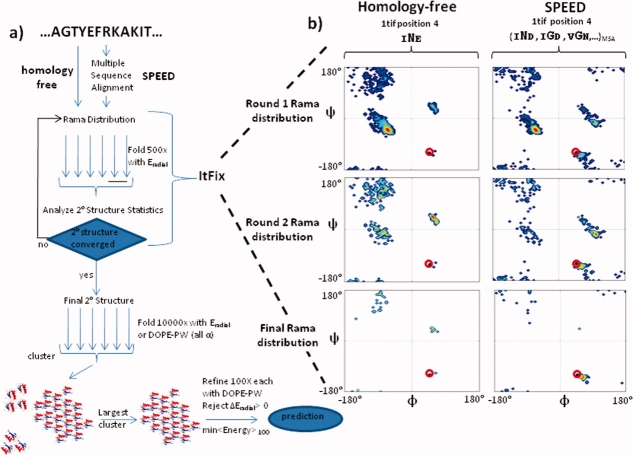
Figure 1.

Structure prediction protocol. (a) The 2° and 3° structure prediction protocol for homology-free modeling uses the target sequence to generate a Rama sampling distribution, whereas SPEED uses a distribution that is averaged over a MSA. The ItFix algorithm iteratively defines the 2° structure, and clustering and refinement are used to predict 3° structure. (b) The Rama distribution for position 4 of the sequence of 1tif is shown for representative rounds of ItFix for homology-free and SPEED sampling. The native ϕ,ψ angles are denoted as a red circle.

Results

Overview

Figure 1(a) provides an overview of both the homology-free and SPEED structure prediction methods using the ItFix 2° structure fixing procedure. The fundamental difference between our original homology-free protocol and the new SPEED protocol relates to the Ramachandran (Rama) φ,ψ sampling distribution. In the homology-free protocol, the distribution is generated only from the target sequence, whereas in the new protocol, the distribution is constructed from an MSA of the target sequence. At the beginning of the ItFix procedure, no 2° structure is fixed, and the φ,ψ distribution at each position reflects all 2° structure types, although the distribution is contingent on the amino acid identities of the neighboring positions [Fig. 1(b)]. Through rounds of folding (Monte Carlo simulated annealing, MCSA) using an energy function that promotes hydrophobic burial and that penalizes polar burial (Methods), the 2° structure options, helix, strand, or coil, are progressively eliminated when their occurrence in the final collapsed structures falls below a ∼0–10% threshold.⁹ Angles originating from the eliminated 2° structure option are excluded in the calculation of the Rama distribution for the subsequent round. The folding and elimination process proceeds until no further 2° structure options can be eliminated [Fig. 1(b), middle and bottom]. The final result is a more restricted Rama distribution across the entire sequence, which greatly reduces the search space.

The final Rama distribution is used to generate a large (10,000) ensemble of 3° structure models. These models are clustered into groups of similar structure, and the models from the largest cluster are selected for refinement and prediction, using our DOPE-PW statistical potential.

SPEED enhanced Ramachandran distributions

At the beginning of the ItFix rounds, the Rama distribution at each position is conditional only on the amino acid identities of the position and its two neighbors. Our homology-free implementation obtains this distribution solely using the target sequence. For example, N4 of 1tif is flanked by I3 and E5 (denoted _IN_E), with the resulting _IN_E having a homology-free Rama distribution displayed in the left panel of Figure 1(b). The SPEED-enhanced Rama distribution is the sum (with equal weights) of the distributions of all possible three-residue combinations generated from the amino acid substitutions identified by the MSA. For example, the SPEED distribution for _IN_E is the sum of multiple Rama distributions derived from the MSA, such as _IN_D, _IG_D, and _VG_N. At the beginning of the algorithm when no 2° structure option is eliminated, the native Rama region has a small sampling probability in the homology-free distribution [Fig. 1(b), red circle, P = 0.01), and the predominant Rama region is right-handed helix (P = 0.6). By contrast, the native Rama region has a ∼20-fold larger probability in the equivalent SPEED Rama distribution. Also, at the end of the ItFix rounds, the SPEED probability of the native Rama region has nearly doubled compared with the homology-free probability (P = 0.37 vs. 0.21). The native Rama probability enhancement due to ItFix, thus, is significantly improved by the MSA-based procedure.

To illustrate the benefit of using SPEED, we quantify the enhancement across all positions in the folding targets by comparing the native Rama probability of the homology-free distribution to that of the SPEED-derived distribution (Fig. 2). This analysis proceeds by partitioning the Rama map into four broad regions [Fig. 2(a)]. More refined divisions of the Rama map exist, but this division into four regions may be the most refined definition with clear borders. The quality of SPEED-derived distribution is quantified as the percentage of positions with high probability of the native Rama region (P > 0.25). This percentage is a useful metric because any position with a low native Rama probability is an obvious candidate for improvement.

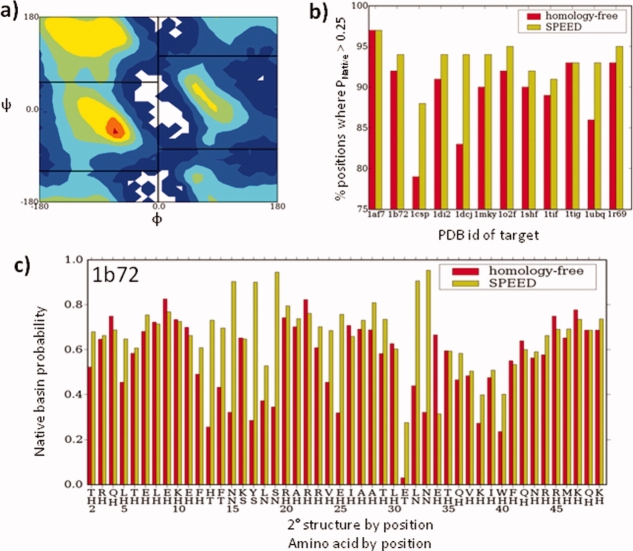
Figure 2.

SPEED-enhanced φ,ψ sampling distribution. (a) Rama space is divided into four coarse regions for analysis. (b) The percentage of residues with probability exceeding 0.25 for the native Rama region is increased for SPEED for all targets, particularly 1csp and 1dcj. (c) For 1b72, the probability of the native Rama region is greatly enhanced using SPEED.

Compared with the homology-free Rama distributions, the new procedure decreases the percentage of residues having a nonnative Rama propensity for 10 of the 12 targets studied [Fig. 2(b)]. The two exceptions remain unchanged because their homology-free distributions already are very good. The two targets with the largest improvement in Rama distribution are 1csp (78 → 86%) and 1dcj (84 → 94%). In particular, the homology-free Rama distribution for 1dcj contains serious flaws due to the aforementioned proline-glycine pair in the second α-helix and for residues in the turn separating the second helix and third strand [Supporting Information Fig. S1(a)]. SPEED overrides the nonnative propensity of G46 in the second helix (P = 0.21 → P = 0.62) and also enhances the E52 turn position's native propensity (P = 0.01 → P = 0.32).

In addition to the moderation of outliers, SPEED enhances the native Rama propensity when it is already high, as is the case for 1b72. Here, the native Rama probability at only 1 of the 10 coil positions (E31) falls below the 0.25 threshold [Fig. 2(c)]. Its native-like probability is only P = 0.03 in the homology-free distribution but increases to P = 0.23 in the enhanced distribution. In addition, the native Rama probability in the SPEED-derived distribution is 2-fold higher than the homology-free distribution in 7 of 10 coil positions. Similar improvements for other targets can be seen in Supporting Information Fig. 1.

The exceptions to this trend generally emerge for positions which already have a very strong native-like propensity in the target sequence. An illustration of this effect is the left-handed turn position G10 in 1ubq. Because glycine favors the native left-handed turn basin more than any other residue, any substitution lowers the native Rama probability [Supporting Information Fig. S1(b)]. Nevertheless, the decrease in native probability due to the use of SPEED is on average is much smaller than the benefit across the entire sequence (Fig. 2, Supporting Information Fig. S1).

ItFix 2° structure

The 2° structures of the final models are identified using the DSSP program for 2° structure determination.¹⁹ Because DSSP-identified β-strands must be involved in β-sheet networks with optimized hydrogen bonds, we lower the strand-fixing threshold with no noticeable decrease in fidelity compared with our previous study. In many cases, the fidelity for specifying 2° structure is higher. This increase is particularly evident for the all-α targets, where the β-strand option is eliminated at every position within the first two rounds as a result of the β-strand probability vanishing (P < 0.005) at every position (in the first round for 1af7 and 1b72; in the second round for 1r69). The same accuracy is found for the helical regions of the αβ targets.

Improvement in 2° prediction accuracy

The 2° structure prediction accuracy using SPEED compares very favorably with the popular 2° structure prediction methods SSPro¹³ and PSIPRED¹² (Table I). When predicting 2° structure at the level of helix, extended or coil (three options, termed Q3), ItFix-SPEED is more accurate than its homology-free ItFix counterpart (average accuracy 84 → 88%). Most of this improvement is because of to 1csp (79 → 87%) and 1dcj (45 → 83%), the two targets with the largest improvements in Rama distributions because of SPEED [Fig. 2(b)]. The 2° structures for the all-α targets already are predicted to high accuracy using the homology-free ItFix, so the average improvement because of SPEED is small (93 → 96%), with the exception of 1b72 where the improvement is more substantial (88 → 96%). The one exception is 1di2, which is discussed in the 3° structure prediction section later.

Table I.

SPEED 2° Structure Prediction Comparison^a

Protein				Rama enrichmentb (angles/residue)		2° Structure accuracyc Q3 (Q8)
PDB ID	Size	Fold	NEFFd	Hfree	SPEED	ItFix	ItFix SPEED	SSPro	PSI-PRED
1af7	69	α	7.3	1426	5599	97 (86)	96 (88)	86 (81)	90
1b72	50	α	5.7	1384	4229	88 (84)	96 (96)	68 (72)	84
1csp	67	β	6.0	1069	2365	79 (67)	87 (70)	75 (67)	88
1di2	68	αβ	6.8	1230	4964	88 (79)	66 (54)	74 (75)	97
1dcj	72	αβ	7.0	1059	4381	45 (29)	83 (65)	65 (56)	89
1mky	77	αβ	5.0	1572	3947	86 (70)	83 (65)	87 (71)	90
1o2f	77	αβ	5.5	1059	4506	78 (69)	84 (73)	79 (66)	75
1r69	61	α	7.5	1036	5058	93 (89)	97 (89)	74 (72)	92
1shf	59	β	7.1	774	3213	76 (56)	71 (51)	85 (69)	80
1tif	57	αβ	4.4	1349	3233	89 (79)	91 (81)	76 (70)	93
1tige	86	αβ	5.4	1194	3323	83 (70)	N/A	69 (67)	83
1ubq	72	αβ	7.7	1152	3405	92 (69)	94 (82)	88 (67)	90

^aTarget sequences are from our previous homology-free ItFix study,⁹ which have been selected from a previous Rosetta prediction study.¹⁷

^bRama enrichment is the positional average of the number of PDB angles used to generate the Rama distribution for each method. The Q3 and Q8 (in parentheses) 2° structure prediction accuracies are reported for the previous homology-free study and SPEED sampling.

^cSSpro and PSIPRED 2° structure predictions are obtained from their respective servers.^39,40 (value in %)

^dN_EFF⁴¹ is a Shannon entropy measure on a scale of 1–20 of the amino acid diversity of the sequence alignment (1 = single amino acid, 20 = all amino acids are equally likely).

^eFolding of 1tig could not converge in reasonable amount of time because radial terms could not be satisfied in a small number of MCSA steps.

More impressive is the increase in accuracy for the prediction of 2° structure at the more refined Q8 level where coil is subdivided into six DSSP-identified subtypes (this level of prediction is unavailable with PSIPRED). For 1b72, the overall Q8 accuracy increases (84 → 96%) using SPEED with a >0.95 probability assigned to the native Q8 value at every position in the second coil region. Two other targets that have substantial improvements in Q8 accuracy are 1dcj (29 → 65%) and 1ubq (69 → 82%). Most of the Q8 improvements for 1dcj arise from the same helix and strand improvements found for the Q3 values, whereas the Q8 improvements for 1ubq are due almost exclusively to better turn predictions within the coil subtype.

Energy functions

We continue to use a reduced C_β model that includes the backbone heavy atoms, backbone amide hydrogen, and the side chain C_β, and a slightly modified version of the DOPE-PW energy function.⁹ This energy function is a pairwise additive statistical potential based on the observed distance distributions in the PDB. In addition to distinguishing each type of atom, the energy function classifies each interaction according to residue type, 2^o structure assignment, and side-chain orientation.

In the prior ItFix treatment, the 2° structure assignment at a position is the same assignment as in the original PDB structure from which the last ϕ,ψ pair is selected at this position. Here, the 2° structure is specified using a geometric definition of 2°structure that is applied in each energy calculation (i.e., in the application of the strand-strand terms, helix-helix terms, etc.). A residue is considered to lie in a helix if it is situated in a block of more than four residues in a row satisfying the following criteria:

The minimum distance between the hydrogen bond donors and acceptors is described by the distance criterion from the hydrogen bond potential of Kortemme et al.,²⁰

In addition to this distance constraint, the hydrogen bond energy function also considers the influence of hydrogen bond orientation. The following term is used to describe the orientation between two covalent bonds, an example being the backbone carbonyl (C=O) bond and amide bond (N—H) orientation:

In this equation, ρ₁₂ represents the angle between the 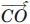and 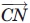vectors, and ρ₂₁ represents the angle between the 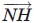and 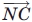vectors. We impose a 90° minimum on ρ to maintain a planar sheet network for both parallel and antiparallel strand orientations.

Our previous study⁹ finds that the statistical potential alone often is incapable of generating a large proportion of well-collapsed models for the targets that contain β-sheets. These simulation models commonly contain attributes that are uncharacteristic of real proteins, such as buried polar residues, unpaired buried β-strands, and a high radius of gyration of C_α atoms (Rg). Buried polar residues and buried unpaired β-strands are symptomatic of an energetic benefit allotted for the close pairing of nonpolar residue C_β atoms and the lack of penalty for the close pairing of polar and nonpolar residue C_β atoms. Thus, the prior treatment allows a strand to be buried in the hydrophobic core of a model so long as it contains a sufficient number of nonpolar residues. High-Rg models can be low in energy because of highly optimized substructures, such as β hairpins, which are formed at the expense of integrating the entire chain into a properly-collapsed model.

Adding a penalty for the burial of polar residues impedes the generation of low-Rg models, and forcing a lower Rg on the chain can worsen the burial of polar groups and β-strands. For this reason, in addition to Rg, two radial terms are included to encourage the proper global collapse of the entire chain. Radial uniformity (Ru) is the standard deviation of the distances of Cα atoms from the Cα center of mass (cm),

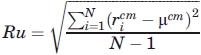where 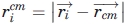, and 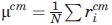. The Ru term is necessary because small globular single-domain proteins rarely have a completely buried chain segment, but instead have an amphipathic alternation between exposed and buried side chains. Enforcing a small value of Ru prevents any portion of the chain from being too close to the center of mass and, therefore, diminishes the propensity for the burial of entire 2° structure units in the core of the model. Rg and Ru are minimized to create a collapsed chain with no completely buried chain segments.

A third radial term, the ratio of the Rg of the nonpolar C_β atoms to the Rg of the polar Cβ atoms, is called burial ratio (Br):

Most small proteins have the nonpolar C_β atoms closer to the center of the protein, whereas the polar C_β atoms are more likely to be on the exterior, so a Br value less than unity captures the global hydrophobic burial of globular proteins. The global burial induced by the Br term contrasts to the local optimization of statistical potentials, which can optimize local subsets of hydrophobic atom pairs at the expense of global burial.

We multiply the three radial terms to obtain the overall scoring function, where E_{DOPE-repulsive} is sum of the positive (repulsive) DOPE terms,

Each MCSA simulation is repeated using E_radial until the Br is less than 0.80. We cap the minimum value of Ru at 2.5 Å, because it is very easy for the chain to fold into a ring structure with Ru close to 0. The multiplied radial terms have a coefficient of 100, so that their combined magnitude is significant relative to the repulsive part of DOPE.

The radial terms are used throughout the ItFix algorithm until the 2° structure is determined. For the final round of folding (10,000 models), if the 2° structure is all-α, the DOPE-PW energy function is used, otherwise the E_radial energy function is used. The final model refinement process uses the DOPE-PW energy function for all targets.

Improvement in 3° structure

SPEED significantly improves the quality of 3° models compared with the homology-free treatment (Table II). The model with the lowest C_α-RMSD (best model) is lower for SPEED in every case except 1di2. Because the best model is not always a very reproducible metric of over-all performance, we consider instead the fraction of final structures below 5 Å C_α-RMSD to the native structure (Fig. 3). This fraction is on average several times greater for SPEED than from the homology-free approach when all other folding parameters (2° structure assignment, energy weighting coefficients, etc.) are identical (Table II, last column). The SPEED folding ensemble for 1ubq contains six times more native-like models than the homology-free ensemble. For four out of the twelve targets, the homology-free distribution produces no models below 5 Å, and hence, the SPEED enhancement factor is effectively infinite. Even so, improvement also is evident across all ranges of C_α-RMSD. For 1b72, the addition of SPEED improves the 3° structure ensemble such that 83% of the models are less than 5 Å Cα-RMSD to the native structure [Fig. 3(b)], which compares favorably to 76% of the homology-free models falling below that threshold. We note that in these direct comparisons of the 3° structure prediction accuracy between homology free and SPEED Rama distributions, the SPEED 2° structure assignments are used in the homology free Rama distribution. Because the SPEED 2° structure is typically more accurate, in reality the 3° structure accuracy enhancement due to SPEED is much larger.

Table II.

3° Structure Prediction

Protein				3° Structure accuracy (values in Å)
PDB ID	size	fold	NEFF	Previous ItFixa	ItFix-Hfreeb	ItFix- SPEEDc	Cα-5.0Xd
1af7	69	α	7.3	2.9 (2.5)	2.5 (2.5)	2.6 (1.6)	1.2
1b72	50	α	5.7	3.5 (1.6)	3.6 (1.7)	3.5 (1.6)	1.1
1csp	67	β	6.0	10.5 (6.0)	NC (4.6)	5.2 (4.1)	4.2
1di2	68	αβ	6.8	6.1 (4.6)	NC (6.8)	NC (6.6)	N/A
1dcj	72	αβ	7.0	13.3 (7.6)	NC (5.9)	5.3 (4.6)	∞
1mky	77	αβ	5.0	6.9 (6.1)	NC (4.4)	5.2 (4.2)	∞
1o2f	77	αβ	5.5	11.2 (5.8)	NC (6.7)	NC (4.2)	∞
1r69	61	α	7.5	4.2 (2.4)	3.7 (2.1)	3.5 (1.6)	1.8
1shf	59	β	7.1	12.2 (6.7)	NC (6.2)	NC (3.8)	∞
1tif	57	αβ	4.4	11.3 (4.2)	5.7 (3.7)	5.4 (3.2)	4.3
1tige	86	αβ	5.4	6.4 (5.3)	N/A	N/A	N/A
1ubq	72	αβ	7.7	5.3 (3.1)	4.4 (3.6)	2.6 (1.9)	6.0

^aThe C_α-RMSD to the native of prediction based on energy and best model (in parentheses) from our previous homology-free ItFix study.⁹

^bFolding with the homology-free Rama distribution and with the final SPEED 2° structure (2000 trajectories), cluster, and refinement prediction and best model (in parentheses).

^cFolding with the SPEED Rama distribution with final SPEED 2° structure (10,000 trajectories), cluster and refinement prediction and best model (in parentheses).

^dRatio of the percentage of models below 5.0 Å C_α-RMSD to native of SPEED (column 7) to homology-free (column 6).

^eFolding of 1tig could not converge in reasonable amount of time because radial terms could not be satisfied in a small number of MCSA steps.

Figure 3.

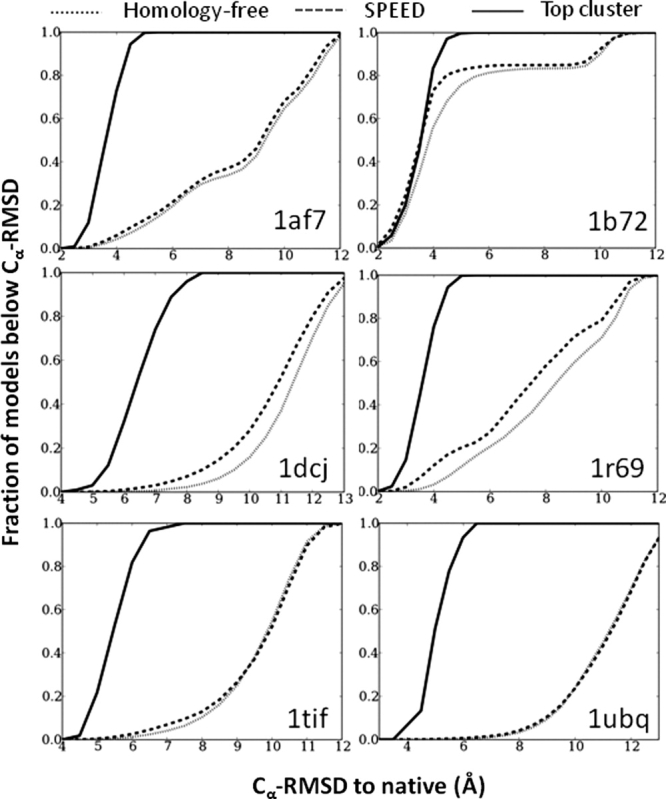
Improvement in 3° structure prediction using SPEED. The percentage of models with a C_α-RMSD to the native below a cutoff level (x-axis) provides a comparison of the overall accuracy of the folding ensembles. The top cluster (solid line) from SPEED is much better than the entire SPEED ensemble (dashed line), which is better than the ensemble generated using the homology-free ItFix Rama distribution with the SPEED-generated 2° structure assignments (dotted line).

Compared with the β and αβ targets, the three α targets have the most native-like ensembles for both homology-free and SPEED methods, and, hence, this class yields the smallest enhancement factor. Conversely, the β and αβ targets produce a very small fraction of native-like models for both SPEED and homology-free methods but have the largest increase in native-like models due to the use of SPEED (Table II). Neither the SPEED nor homology-free methods generate native-like models for 1di2, most likely because it is considerably more prolate in shape than the rest of the proteins, and the radial energy terms (Ru, Rg, Br see Methods) enforce a spherical bias (Supporting Information Table S1).

An obvious question is whether the increase in the accuracy of 3° structure prediction found with SPEED emerges from the improvement of a few residues with low homology-free native (φ,ψ) probability or from small improvements across the entire sequence. Although it is impractical to test the effects of SPEED one residue at a time, the general behavior is illustrated for 1dcj, the protein for which the use of SPEED introduces the largest improvement in the accuracy of both 2° and 3° structure predictions. Without SPEED, we fail to predict the second helix, which contains the Pro-Gly combination and has low intrinsic helicity. Even with the 2° structure of this helix correctly fixed, the 3° accuracy still is inferior without incorporating SPEED (Table II), presumably due to the extremely low homology-free turn probability at position 52 compared with the SPEED-based probability (P_hfree=0.02; P_SPEED=0.32). Hence, we believe that the larger improvements due to SPEED probably can be localized to a few critical positions. However, the improvement of near native structures (e.g., RMSD less than 3–5 Å) likely arises from the cumulative effect of enhancement at many positions.

Averaging the energy function across the MSA

Analogous to the SPEED-improved Rama distribution, we have also tested an energy function that is averaged over the MSA to incorporate additional sequence information, specifically via sequence correlations in the long-range interactions. The analysis of correlated mutations in sequence alignments has been used previously in other prediction and design methods.^21–24 The new energy function uses the original statistical potential and the same pairwise distances, D_i,j, between the pairs of amino acids. However, the new energy for each (i,j) residue pair now is the average energy calculated using the distance D_i,j and statistical potential appropriate for the amino acid pair found in each sequence in the MSA. This procedure includes extra long-range information by incorporating the pairwise amino acid correlations inherent in each aligned sequence.

Although this method is intellectually appealing, the results are variable. We suspect that for each interaction, the optimal (lowest energy) separation distance for each contact varies too much for the different combination of residues found in the sequences in the MSA. Consequently, the energy surface averaged across the sequences in the MSA has a shallower minimum compared with the energy function calculated using only the target sequence.

Cursory tests using a single consensus sequence with the standard energy function also fail to produce uniformly superior results. However, we maintain that a careful and clever implementation or extension of these ideas could yield strong improvements.

Clustering

The enhancement of the fraction of native-like models obtained using SPEED has additional implications for 3° structure prediction. In our previous homology-free study, the predicted structure is the lowest energy model from the final folding ensemble. But, that structure is native-like (<5 Å) only for about half of the targets, failing mostly when few or no accurate models are generated. Although the use of SPEED increases the proportion of accurate models, energy alone is insufficient for reliably choosing the best model. This situation is common in structure prediction. As a result, clustering methods are frequently used because repeatedly occurring low energy conformations are typically more accurate than structurally isolated low-energy models.²⁵

The lowest energy model from the top cluster for the homology-free and SPEED-based Rama distributions are presented when a cluster exists (Table II). A larger fraction (8/12) of the SPEED-based ensembles contains identifiable clusters compared with the homology-free ensembles (6/12), and their size often is larger as well (Fig. 3). Even when the largest cluster is the best, it may share a similar average contact profile to other less accurate clusters (Fig. 4). For example, the contact profiles of the largest two clusters of 1b72 display almost identical contacts, but decidedly different values for the average C_α-RMSD to the native (cluster 1, < 4 Å; cluster 2, > 10 Å). This result is due to the simplicity of the 1b72 fold (a 3-helix bundle), which permits a low energy fold that is a pseudo-mirror image fold of the native and, therefore, has similar contacts and similar average energy. Given this energetic similarity, the Rama distribution determines the favorability of the native conformation, with the SPEED protocol succeeding to a greater extent than the homology-free protocol.

Figure 4.

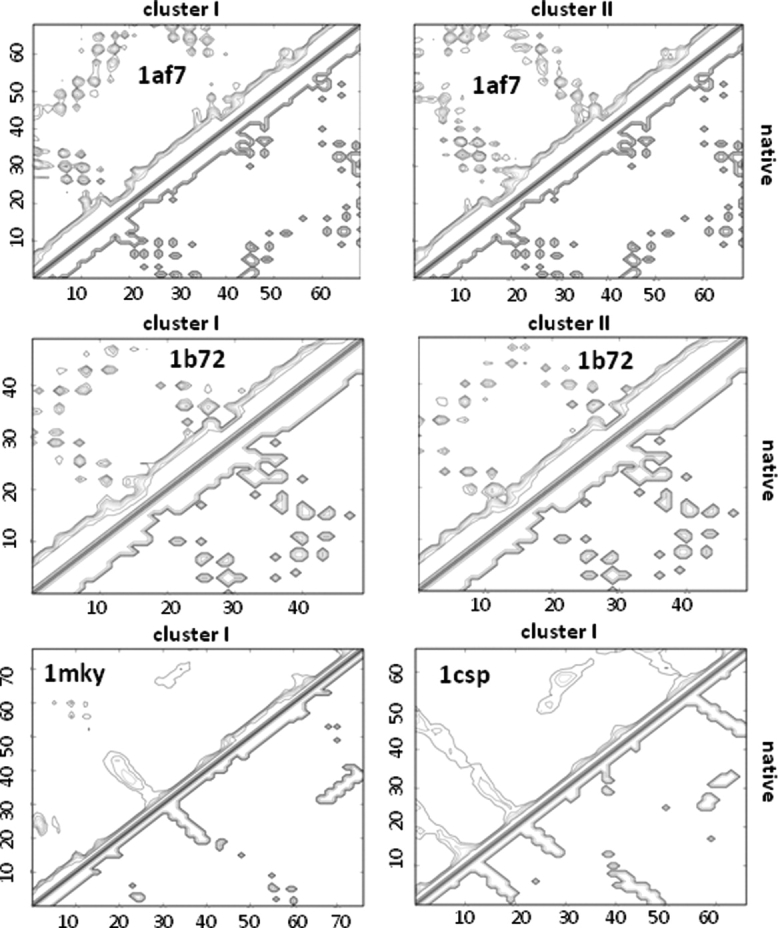
Comparison of contacts for the top clusters of several targets. Each map is a C_α-C_α contact matrix with a 10.0 Å distance cutoff for α targets (1af7, 1b72) and a 8.0 Å distance cutoff for the αβ and β targets (1mky and 1csp). Contacts of the native model are presented on the lower right of each map. The largest cluster for 1af7 has the most native contacts and has an average C_α-RMSD to the native less than 4 Å. The next largest 1af7 cluster, which has an averge greater than 10 Å C_α-RMSD to the native, exhibits many native and nonnative contacts. The largest 1b72 cluster is the most native in terms of C_α-RMSD (<3Å average), but contains identical contacts to the next largest cluster (>10 Å C_α-RMSD to native average) that is the mirror-image fold of the native. The contacts matrices of the top clusters of 1mky and 1csp are both very native-like.

Confidence assessed from reproducibility

Although numerous methods exist for structure prediction,^{6–8,17,26,27} the quantification of the accuracy and confidence of a prediction is a crucial, but often elusive component. Template-based methods typically infer confidence from the quality of the available information used to generate an alignment and a consensus of aligned models.^28–30 When predicting remote templates, this technique can suffer from a dearth of PDB templates that independently align to the target sequence with high confidence. This situation precludes any meaningful clustering analysis and, therefore, imparts a large uncertainty to model quality.

Template-free prediction methods have an advantage of generating a large number of models that can be clustered. One noticeable feature of our method is the high correlation (R² = 0.85) between the average C_α-RMSD between models in the predicted cluster and the average accuracy (C_α-RMSD to the native) of the models within the cluster (Fig. 5). This trend suggests that template-free models that are reproduced with a high degree of structural similarity tend to be proportionately more accurate than models that are structurally further removed from their closest neighbors. Noticeably, the average C_α-RMSD between models in a cluster is typically 1 to 2 Å lower than the average C_α-RMSD to the native of the cluster, suggesting that the top cluster has converged upon a stable but slightly nonnative energy minimum. Nonetheless, this difference can be factored in when quantifying the predicted accuracy and may be diminished by improvements in the energy function and sampling distributions.

Figure 5.

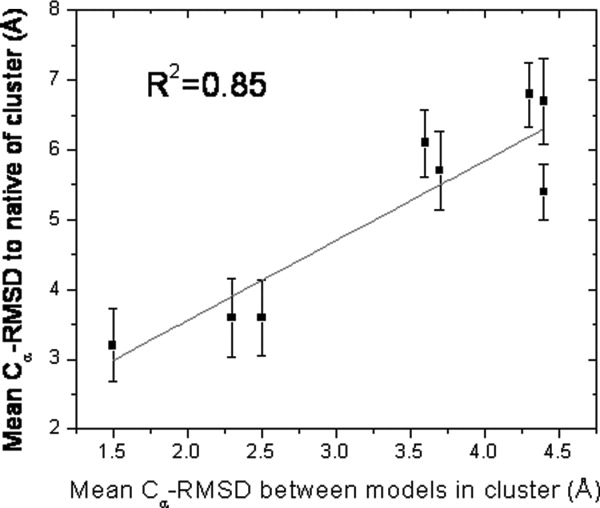
Assessing global accuracy from reproducibility of the top cluster. The mean C_α-RMSD to native of the top cluster is strongly correlated with the mean C_α-RMSD between the models in that cluster, indicating that the latter metric can be used as a measure of predicted model's accuracy.

In addition to global accuracy, the residue level RMSD at each position is calculated to quantify the confidence of the prediction for each amino acid in the protein (Fig. 6). Specifically, the average and standard deviation of the distance at each position between the aligned models in the cluster are highly correlated to the respective average distance and standard deviation at each position between the aligned cluster models and the native model, suggesting that the accuracy and uncertainty at each position in the protein can be predicted.

Figure 6.

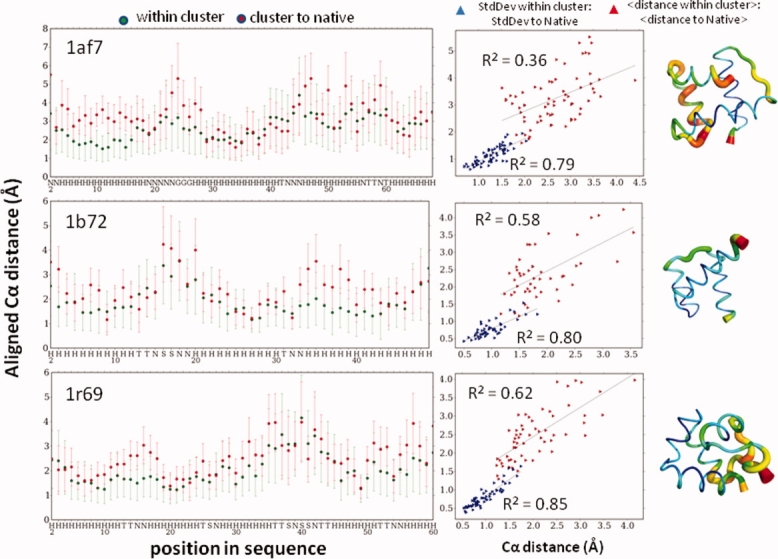
Assessing local accuracy from reproducibility of top cluster. Position-resolved model accuracy and confidence. The average aligned distance between all models in the predicted cluster and the standard deviation of that distance is determined for each position. These values are highly correlated to the respective average aligned distance and standard deviation at each position between each model in the cluster and the native structure. The standard deviation for each of these values also is highly correlated, suggesting the ability to use clustering to determine confidence for each position in a predicted model.

This finding has implications for other template-free methods, which may suffer method-specific difficulties when trying to quantify the confidence of model predictions. Most template-free methods rely on large fragments from PDB models.^6,14,17 In the cases where the number of such fragments is limited, a bias would be introduced due to the highly restricted nature of the conformational search. In other words, independently converging on very similar models may not be as meaningful when the likelihood of sampling the same conformation is very high. Because the conformational changes in ItFix feature the rotation of only a single pair of ϕ,ψ angles, a resulting ensemble consisting of a cluster of very similar models can be treated with higher confidence given that the accessible conformation space is much larger than in fragment based methods. Similarly, the bias likely is even weaker for all-atom physics-based simulations⁸ and ab initio folding simulations,⁷ which have the least restricted conformational search. ItFix-SPEED may combine the best of both a restricted and unbiased conformational search in regards to assessing accuracy from the structural diversity of the largest cluster.

Performance in CASP8

We have applied an early version of the ItFix-SPEED protocol in the 2008 Critical Assessment of Structure Prediction (CASP8) for the human/server targets when a suitable template from the PDB could not be identified by the threading program RAPTOR,^31,32 one of the top performing entries in the server category. Of these targets, the 120 residue T0482 is the only small, globular, single-domain free-modeling target with no confident templates, making it a prime candidate for the ItFix-SPEED methodology. This target has been subjected to multiple rounds of ItFix-SPEED, and our final three submitted models are very similar with highly accurate 2° and 3° structures [Fig. 7(a)]. Our predicted 2° structure is slightly improved over the PSIPRED¹² prediction. Because of time constraints, we initially assigned PSIPRED's high confidence (>90%) predictions at ∼10% of the positions (total wall clock time for prediction was under 12 hr from start of prediction to submission). When the central 100 residues (ignoring the solvent exposed ends of the NMR structure) of these models are aligned to the now published structure, the C_α-RMSD to native is 4.8 Å. Hence, our algorithm is able to confidently predict the correct structure without any false positive submissions. In addition, our top model has the lowest C_α-RMSD among all submitted #1 models. We have performed commendably for other challenging template-free modeling targets, such as the D1 subdomain of protein T0405 [Fig. 6(b)]. These results constitute strong evidence of the predictive capabilities of the ItFix-SPEED algorithm.

Figure 7.

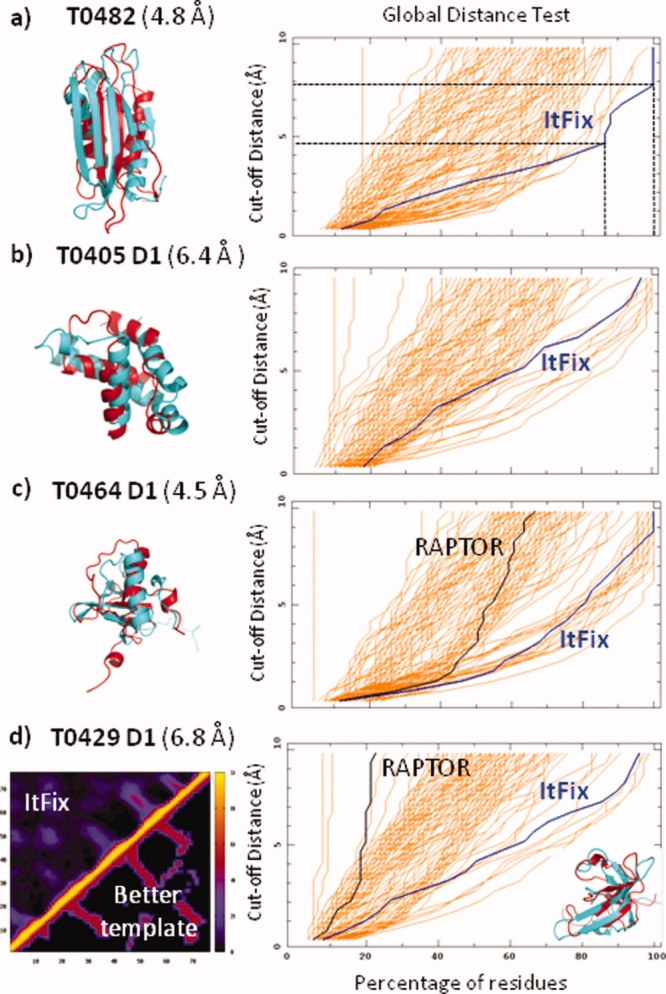
ItFix-SPEED blind predictions in CASP8. (a) 2° and 3° structure prediction of target T0482. The ItFix 2° structure prediction compares favorably to the native at 84% accuracy, which is slightly superior to the 82% accuracy of PSIPRED. The Global Distance Test (GDT) value is the percentage of the residues within a cutoff distance of the native structure. This cutoff distance is the y-value on the plot (e.g., for the ItFix prediction, 83% and 100% of the residues are predicted to within 4.7 and 7.8 Å of the native structure, respectively). The GDT trace for the ItFix prediction (blue line) is the rightmost of all the Model 1 predictions indicating that the method is able to predict more residues with higher accuracy. In addition, the Cα-RMSD to native is the lowest of all the Model 1 predictions. The Itfix-SPEED prediction for (b) the entire Domain 1 of target T0405, and (c) the 24-residue insertion in RAPTOR's predicted template for T0464. (d) Itfix-SPEED selection of the best template identified by RAPTOR based on average predicted tertiary contacts. Contact map, upper left: ItFix average contacts for the final structures from 100+ folding trajectories; lower right: contacts of one of RAPTOR's lower ranked templates, which is the closer to the native structure than its top ranked template, which has a less similar contact map. Values in parenthesis are the Cα-RMSD between predictions and the native structure. GDT plots are taken from the CASP8 website (http://www.predictioncenter.org/casp8/index.cgi).

Our participation in CASP8 also includes predictions for sequences that have only poor templates and are considered template-free modeling targets. For target T0429, RAPTOR chooses multiple homology-based templates, but it is uncertain as to which template is correct for the C-terminal domain. ItFix-SPEED folding simulations for this domain have been used to compare the average contact matrix of our folding simulations with the contacts of each possible template [Fig. 7(d)]. This process has enabled us to choose a better template (T0429-2ckk) than RAPTOR's top scoring template.

The SPEED-based sampling protocol also has been used to determine the structure of the insertions of unknown structure that are present in RAPTOR-generated models. These situations have been treated by breaking the chain at one end of the insertion and then folding this free end in the context of the entire protein. The most successful outcome is for a 24-residue insertion for target T0464, where our prediction ranks as one of the top submissions [Fig. 6(c)].

Discussion

Our computationally rapid algorithm using only single (φ,ψ) dihedral angle pivot moves can generate very accurate predictions of both 2° and 3° structures without relying on any known structures, templates, or fragments. For the test set, we typically predict 2° structure with ∼90% accuracy, while the best 3° structure for 4/12 of the targets have Cα-RMSD less than 2 Å. Hence, given intelligent search strategies and scoring functions, C_β representations can be used to accurately predict 2° and 3° structures.

Structure prediction is beyond current capabilities for the vast majority of the families identified by large-scale sequencing efforts.^4,33 The number of sequences with minimal sequence similarity to known structures is increasing at a rate that outpaces our ability to identify new families.⁴ Currently, only about one third of the single-domain architectures have known folds.⁴

Conclusion

The ItFix-SPEED procedure is well suited to contribute to mapping the protein universe, particularly for low homology sequences. Because our procedure uses only MSAs, it can take advantage of the 10⁷ known sequences and is not limited to the ∼10⁴ unique structures in the PDB. For CASP8 target T0482, no member of its family had a known structure, although its fold is not new. The ItFix-SPEED procedure accurately predicted its structure using only 50 nonredundant sequence homologues and no structural information. Furthermore, the ItFix-SPEED procedure is able to quantify the global and local accuracy of its prediction from the reproducibility of the trajectories, a highly desirable feature from the perspective of users of any sequence database annotation.

Methods

Generation of sequence alignments

Sequence alignments are generated by PSI-BLAST³⁴ using the executables from NCBI on the nonredundant database. An intersequence similarity cutoff of 65% is imposed with CD-HIT.³⁵ PSI-BLAST searches are performed in three passes with an E-value cutoff of 1.0. We choose only sequences that cover more than 90% of the target sequence length and have gaps that span at most one position. These constraints are chosen such that sequences are very likely to approximate the same structure as the target. As a result of these constraints, the average E-value of each sequence in an alignment is orders of magnitude lower than 1.0.

SPEED sampling

The MSA is used to generate an amino acid substitution matrix at each position in the target sequence. Any amino acid that occurs in more than 10% of the alignments is included at that position. If a position only has only one amino acid in its substitution matrix, the amino acid occurrence threshold is decremented by 1% until there is more than 1 substitution, with the exception of proline, which is kept as the sole amino acid at a position down to 5% probability as long as there are no neighboring positions with prolines that occur at a greater probability. If proline is the sole amino acid in the MSA-generated substitution matrix, we mutate the target sequence at that position to proline. In all other cases, the sequence used during folding remains the same as the target sequence.

We initially tried calculating the SPEED distribution of a position by adding the Rama distributions at that position for each sequence in the alignment. The SPEED distributions created from this method, however, are more similar to the homology-free distribution because the target sequence amino acid often has the highest-probability in the alignment and would be weighted proportionately in the SPEED distribution. Using a substitution matrix, conversely the other hand, weights all amino acids above a threshold equally, thereby rendering the resulting Rama distribution less similar to the homology-free distribution.

Because the statistics for the distributions constructed from an MSA permit many different combinations of amino acids, the area of the Rama map with vanishing probability tends to be much lower for the SPEED distribution than previously used because of the added MSA-identified combinations. In fact, the average number of angles per position used to generate a SPEED distribution is three- to five-fold larger than the number of angles used to generate a homology-free distribution (Table I). As seen in Figure 1(b) and the subsequent predictions, this added diversity does not dilute the specificity of the conformational search; indeed the distributions are more native-like.

Ramachandran sampling

Our prior treatment used a sampling of specific ϕ,ψ angle pairs from a library generated from high resolution crystal structures, conditional on the 2° structure and nearest neighbor amino acid identities. The present study likewise employs a distribution of ϕ,ψ angles with the same dependencies, but instead of sampling from a large list of angles extracted from PDB models, the ϕ,ψ angles are chosen from a Rama distribution that is generated for each position based on the amino acid identity and the 2° structure specification of that position and of its nearest neighbors. Thus, Rama distributions are calculated for the central residue in each of the distinct 8000 combinations of three contiguous amino acids, conditional on the amino acid identity and on the 2° structure of all three residues. Because the ItFix simulations consider six possible categories of 2° structure for the construction of the sampling distributions (H: helix, E: strand, C: coil, A: everything, O: not helix, and Q: not strand), 1,728,000 possible Rama distributions are constructed to describe the possible 8000 amino acid triplets. Each Rama distribution has 72² 5° × 5° bins, and each bin is assigned a probability that is determined by frequency of occurrence of these backbone dihedral angles in the PDB for the specific conditions of amino acid identities and 2^o structure. A Rama distribution accommodates the increase in PDB-derived angles introduced by SPEED without increasing the system memory, as occurs when each angle is explicitly stored in memory.

The sampling of ϕ,ψ angles begins by selecting a bin in Rama space according to the probability assigned to that bin (e.g., a bin that contains 1.5% of the angle counts for the distribution at that position has a 0.015 probability of being selected). This bin selection is followed by the selection of a random angle uniformly from within the 5° × 5° window of that bin. The Rama distribution of the central residue of the triplet INE (position 4 in 1tif) with all allowed 2° structures is an example of one such sampling distribution [Fig. 1(b), top]. If the subsequent round of ItFix eliminates a 2° structure option at a position, the Rama distribution at that position is changed accordingly [Fig. 1(b), middle, bottom].

Clustering algorithm

After the ItFix protocol generates a predicted 2^o structure, a further 10,000 folding simulations are run to maximize the exploration of conformational space. The pairwise C_α-RMSD matrix of the resulting 10,000 models is used to cluster the ensemble into groups of models that all align to each other below a C_α-RMSD cutoff, an approach that is similar to the SPICKER algorithm.²⁵ Other methods³⁶ cluster according to the C_α-C_α distance instead of the pairwise C_α-RMSD, but we find that the C_α-C_α distances in some cases are highly correlated even though the C_α-RMSD between the models are quite different [Fig. 4(b)].

When identifying clusters, the upper limit of the cutoff distance of the inter-model C_α-RMSD is increased in increments of 1 Å starting at 1 Å until at least five clusters are found, or a 7 Å limit is reached. Every model in the cluster must have a C_α-RMSD to every other model in the cluster that is less than the cutoff distance. Targets with predicted all-α 2° structures have a minimum cluster size of 5%, whereas the minimum size for targets with other predicted 2° structure types can be as low as 0.04%. A cluster is eliminated if it contains a model present in a larger cluster. The largest cluster is selected as the predicted model, unless it has an above average energy and there is another cluster with an energy that is greater than one standard deviation below average. For αβ and β targets, the predicted cluster cannot consist of a fold that contains a predicted β-strand that is not part of a β-sheet.

Model refinement

One of the most important challenges of structure prediction is an effective exploration of conformational space. Ideally an exhaustive refinement is performed for every model generated by folding, but we take a computationally thrifty approach and refine only the models in the largest cluster of each target. Refinement consists of the same move set and energy function as folding, with the addition of the fact that we reject moves that increase the Rg, Br, or Ru of the starting model. Each model in the cluster is refined 100 times, and the model with the lowest average energy among all the refined models is chosen at the prediction listed in Table I.

Parallel scripting with swift

The ItFix-SPEED algorithm has been implemented, tested and evaluated³⁷ using an innovative parallel scripting language called Swift.³⁸ The Swift runtime system automates parallelization, data management, and error recovery, and supports execution on a wide variety of parallel computer systems. This allows the composition of flexible structure prediction scripts to address new energy functions and explore algorithm enhancements, and to compare the behavior of the algorithm under a wide range of conditions and parameter settings.

Glossary

Abbreviations:

MCSA

Monte Carlo simulated annealing

MSA

multiple sequence alignment

2^o

secondary

3^o

tertiary.