Table 1.
The method ContDetApprox (left) and the main procedure sWindow (right)
| ALGORITHM ContDetApprox (z, τ, b+, b-) | ALGORITHM sWindow(y, t, ϵ, δ) |
|---|---|
Input: initial state z, length τ of time interval, old boundaries 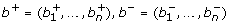
|
Input: initial state y, times t = (t0, ..., tr), error ϵ > 0, threshold δ > 0 |
Output: new boundaries 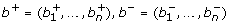
|
Output: probability vectors p0, ..., pr |
| 1 for each branch i ∈ {1, ..., 2n} do | 1 p0 = (1y)T; //start with probability one in y |
| 2 x⟨i⟩:= z; //z is initial state of all branches | 2 for j := 1 to r do |
| 3 end | 3 τj := tj - tj-1; //length of next time step |
| 4 time := 0; | //define Sjfor construction of Wj |
| 5 Δ := step_size; //choose length of time steps | 4 Sj := {x | pj-1(x) >δ}; |
| 6 while time <τ do | 5 numStates := min(10, size(Sj)); |
| 7 for each branch i ∈ {1, ..., 2n} do | //choose numStates random states from Sj |
| //compare current state variables with boundaries | 6 Aj := rand(Sj, numStates); |
| 8 for d = 1 to n do | 7 b+: -∞; b- : +∞; //initial boundaries |
9 if 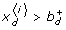 then then
|
8 for each z in Aj do |
10 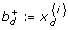 ; //adjust upper bound ; //adjust upper bound
|
//run continuous determ. approximation |
| 11 end | //on z and update boundaries |
12 if 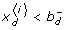 then then
|
9 (b+, b-) := ContDetApprox (z, τj, b+, b-); |
13 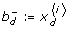 ; //adjust lower bound ; //adjust lower bound
|
10 end |
| 14 end | 11 Qj := generator (Sj, b+, b-); //construct Qj |
| 15 end | //construct diagonal matrix for Wj (cf. Eq. (7)) |
| 16 for m := 1 to k do | 12 Dj := diag(Sj, b+, b-); |
| //choose more/fewer transitions of type Rm | 13 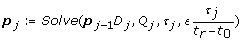 ; //solve Eq. (7) ; //solve Eq. (7) |
| //depending on branch i | 14 end |
| 17 κm := choose(αm(x⟨i⟩)·Δ, i); | |
| 18 end | |
19 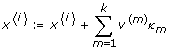 ; //update state (cf. Eq. (11)) ; //update state (cf. Eq. (11)) |
|
| 20 end | |
| 21 time := time + Δ; | |
| 22 end | |
