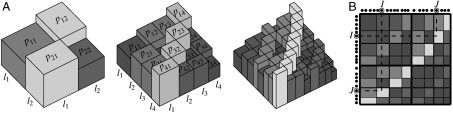
Fig. 1.

Schematic illustration of the multifractal graph generator. (A) The construction of the link probability measure. We start from a symmetric generating measure on the unit square defined by a set of probabilities p_ij = p_ji associated to m × m rectangles (shown on the left). In the example shown here m = 2, the length of the intervals defining the rectangles is given by l₁ and l₂, respectively, and the magnitude of the of the probabilities is indicated by both the height and the color of the corresponding boxes. The generating measure is iterated by recursively multiplying each box with the generating measure itself as shown in the center and on the right, yielding m^k × m^k boxes at iteration k. The variance of the height of the boxes (corresponding to the probabilities associated to the rectangles) becomes larger at each step, producing a surface that is getting rougher and rougher; meanwhile, the symmetry and the self-similar nature of the multifractal are preserved. (B) Drawing linking probabilities from the obtained measure. We assign random coordinates in the unit interval to the nodes in the graph and link each node pair I,J with a probability given by the probability measure at the corresponding coordinates.