Electronic pathway in reaction centers from Rhodobacter sphaeroides and Chloroflexus aurantiacus

Abstract

The reaction centers (RC) of Chloroflexus aurantiacus and Rhodobacter sphaeroidesH(M182)L mutant were investigated. Prediction for electron transfer (ET) at very low temperatures was also performed. To describe the kinetics of the C. aurantiacus RCs, the incoherent model of electron transfer was used. It was shown that the asymmetry in electronic coupling parameters must be included to explain the experiments. For the description of R. sphaeroidesH(M182)L mutant RCs, the coherent and incoherent models of electron transfer were used. These two models are discussed with regard to the observed electron transfer kinetics. It seems likely that the electron transfer asymmetry in R. sphaeroides RCs is caused mainly by the asymmetry in the free energy levels of L- and M-side cofactors. In the case of C. aurantiacus RCs, the unidirectionality of the charge separation can be caused mainly by the difference in the electronic coupling parameters in two branches.

Introduction

Photosynthesis is a reaction in which light energy is converted into chemical energy. The primary process of photosynthesis is carried out by a pigment-protein complex embedded in the membrane, that is, the photosynthetic reaction center (RC). In photosynthetic purple bacteria, the cyclic electron transfer reaction is performed by the RC and two other components: the cytochrome (Cyt) bc₁ complex and the soluble electron carrier protein. The RC is a special pigment-protein complex that functions as a photochemical trap. The precise details of the charge separation reactions and subsequent dark electron transport (ET) form the central question of the conversion of solar energy into the usable chemical energy of a photosynthetic organism. The function of the RC is to convert solar energy into biochemically usable energy. Therefore, we wish to understand which features of the RC are responsible for the rate constants of these reactions.

Insight into the molecular organization of the RC has been derived, initially, from spectroscopic studies and, subsequently, from the development and analysis of high-resolution crystal structures of several photosynthetic organisms. The first RC structurally resolved (3 Å) was of the purple bacterial RC from Rhodopseudomonas viridis [1]. This was soon followed by the elucidation of several other purple bacterial structures. Good progress is also being made toward achieving two- and three-dimensional structures of photosystem II (PSII) crystals. It is surprising that the structures of all the different RCs show a dimeric core with a pseudo-C₂ axis of symmetry.

A remarkable aspect of the RC structures is the occurrence of two almost identical electron acceptor pathways arranged along the C₂ axis relative to the primary charge-separating dimer (bacterio) chlorophyll (Fig. 1). This finding posed a key question: Does electron transfer involve both branches? In the purple bacterial RC, only one branch is active, although the inactive branch can be forced into operation with modification of amino acid side chains on the active branch [2]. Moreover, the charge-separating electron transfer reactions occur with a remarkably high quantum yield of 96%, where, from two possible symmetric branches, only the branch L is active in the electron transfer. This efficiency relies on the rates of the charge-separating reactions being two to three orders of magnitude faster than the rates of the competing reactions.

Fig. 1.

The RC of purple bacteria are composed of three protein subunits called L, M, and H. Dimer P is described by molecule 1. Cofactors in the L subunits are represented as molecules 3 (BChl_L), 5 (BPh_L) and 6 (Q_L); similarly, in the subunits M, BChl_M is described as molecule 2, and molecule 4 represents BPh_M. Cytochrome C serve as a source of electrons for RC

The strong asymmetry imposed on primary charge separation photo-chemistry in the purple bacterial RC results from two homologous polypeptides that function as a heterodimer. A heterodimer is also involved in the core of the RCs of PSI and PSII. However, some RCs, such as heliobacteria [3] and green sulfur bacteria [4], contain two identical homodimeric polypeptides, and electron transfer is potentially bifurcated.

Genetic sequence information has greatly improved the understanding of the origin of the RC proteins. From the sequence analysis, it became clear that the purple bacteria RC is remarkably similar to that of PSII, and PSI was also discovered to have similarity with that of the green sulfur bacteria [5]. Recent structural comparisons between PSI and PSII, for example, show a distinct structural homology, which suggests that even these two RCs likely share a common ancestor [6].

After extensive studies, the rate is now established to be critically coupled to the properties of the bacteriochlorophyll monomer that lies between the donor and bacteriopheophytin acceptor (Fig. 1). The involvement of the bacteriochlorophyll monomer may give rise to multiple pathways for electron transfer [7] and can partially determine the unidirectionality of charge separation along one branch [8, 9].

The chain located on subunit M is inactive in ET, and the highly asymmetric functionality, however, can be decreased by amino acid mutations or cofactor modification. We used this approach to explain the effect of individual amino acid mutation or cofactor modifications on the observed balance between the forward ET reaction on the L side of the RC, the charge recombination processes, and ET to the M-side chromophores [10–14].

The theoretical models describe the charge transfer in RCs using parameters with clear physical interpretations. Some of these input parameters cannot be deduced from independent experimental work. The information regarding the energetic parameters, the medium reorganization energies, the high-frequency modes, and electronic coupling terms can be achieved with quantum mechanical computations. However, until now, these parameters characterizing the RCs have not been available. We thus use the set of parameters that fit the experiments. Several sets of parameters were used to describe a charge transfer in the RC [15–17]. The method for determining the input parameters from theory is by comparison with observed kinetics for different mutated RCs. The problem is that the impact of mutation on the input parameters is not always clear. In this paper, we focus on the electron transfer in two RCs. The first one is the RC of the green bacterium Chloroflexus (C.) aurantiacus. The second is the H(M182)L mutant from Rhodobacter (R.) sphaeroides. Generally, it is believed that RCs have similar structures, where high efficiency of solar energy conversion to chemical energy is based on common electronic properties. The peculiarity of C. aurantiacus RC is that it contains the Bacteriopheophytin (BPh) in the M-branch, where the Bacteriochlophyll (BChl) molecule is placed in the R. sphaeroides RC [18]. The M branch is active in RCs where the BChl molecule is replaced by the BPh molecule. It is thought that this replacement lowers the energy of accessory molecules, which causes branch M to be active. This is not the case for the C. aurantiacus RC.

We adapt in this work the set of parameters that characterizes the observed L-side experimental kinetics of wild-type (WT) RCs of R. sphaeroides very well [16, 17]. The C. aurantiacus RCs and the H(M182)L RC mutant from R. sphaeroides have a structural similarity, but their charge separation kinetics are different. Both these RCs contain BPh pigment in the M-branch at the position where BChl monomer is placed in WT RCs of R. sphaeroides. In contrast with this structural similarity, the H(M182)L mutant reveals the electron transfer through the M branch; in C. aurantiacus RCs, the M-branch is inactive.

Model of reaction center

The RC is an open system. If we describe the RC as a closed system, there ought to be, after some time, a Boltzmann distribution of electron localization on cofactors, and consequently, both branches must be active. To describe the leak of electrons from RC, we have to impose sink parameters into the model. It can be assumed that the system of interest interacts with another part of the overall system with quasicontinuum spectrum, and when an electron is transferred to this subsystem, backward transfer is practically impossible (in the duration of the experiment). There is, for instance, also the possibility of the deactivation of the RC to its ground state. In other words, the system of interest interacts with another part of the whole system, which is not investigated. This part can be assumed to have a continuum spectrum from which the backward electron transfer to the system of interest is not possible in real time. We describe this interaction (channel) by the imaginary part of the effective Hamiltonian, and this imaginary part cannot be neglected in the memory kernel function or in the free electron propagator [19].

Using the standard projection operator techniques [20–23], we can derive a generalized master equation for the populations,

1

where

2

Here, ε_j is the site energy, V_ij are electronic coupling parameters, has the meaning of the life time of the electron at site j in the limit of zero electronic coupling parameters, ω_α is the frequency of the αth mode, 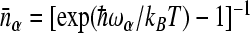is the thermal population of the αth mode, and

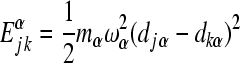3

is the reorganization energy of the αth mode when the system transfers from state to state . Here, m_α is the mass of the αth oscillator and d_jα is the equilibrium configuration of the αth oscillator when the system is in the electronic state j.

To describe the first step of the electron transfer processes in the RCs, we have used the five-site kinetic model of RC. We designate the special pair P as site 1, sites 2 and 3 represent the molecules BChl_M and BChl_L, and sites 4 and 5 then represent the molecules BPh_M and BPh_L (Fig. 1). We assume that we can neglect the backward electron transfer from quinone molecules, and so we use the complex energies of molecules at sites 4 and 5. Based on experimental observations of ET in RC, it is expected that bacteriochlorophyll plays a crucial role in ET. In this five-site model, we have assumed that ET in RC is sequential. It means that the P⁺BChl− state on both the L and M branch is a real chemical intermediate of electron transfer and not only a virtual state, which is used in the superexchange electron transfer [24]. The imaginary part of energy level 1 describes the probability of electron deactivation to the ground state.

Chloroflexus aurantiacus reaction center

We describe the ET in C. aurantiacus RCs by the following kinetic model:

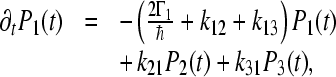4a

4b

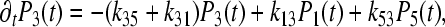4c

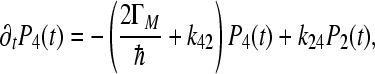4d

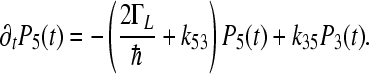4e

Here, we denote 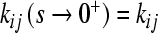and .

We assume that the rate constant that characterizes ET can be described by both a low-frequency medium vibrational mode ω_m and a high-frequency intramolecular vibrational mode ω_c. We will work in the limit where the molecular modes are frozen, 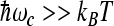. In this regime, the constant k_ij is in the form [16, 25]:

5

Here, 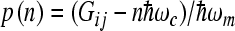, G_ij = ε_i − ε_j, and is the scaled reorganization constant of the high-frequency ijth mode when electron is transferring from the state 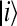to the state 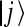, and is the scaled reorganization constant of the low-frequency mode. I_p(z) is the modified Bessel function of order p and 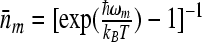. The back electron transfer reaction rate constant can be calculated by using the detailed balance relation and can be expressed in the form .

The quantum yields Φ_L, Φ_M of electronic escape via branch L, M, the quantum yields Φ_G of direct ground state recombination, and 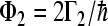deactivation to the ground state from the site 2 cofactor can be characterized for a five-site kinetic model by the expressions

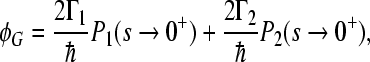6a

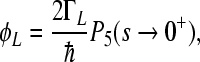6b

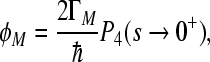6c

where the condition Φ_L + Φ_M + Φ_G = 1 has to be fulfilled. We start with the assumption that Γ₂ = 0; this means that we consider no direct decay of the state into the ground state. The expressions for electron transfer are given by the inverse Laplace transformation. Therefore, we firstly apply the Laplace transformation to P(t) in the system of Eqs. 4, where the Laplace transformation is defined as

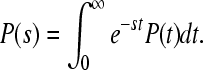7

Next, we apply the inverse Laplace transformation of P(s), where the inverse Laplace transformation is represented by a set of simple poles of P(s). Evaluating it, we obtain

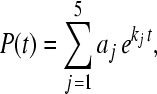8

where a_j are the amplitudes and k_j are the rate kinetic constants describing the electron transfer.

Using the model described above, we would like to find the electron transfer kinetics for the RCs of C. aurantiacus [18], where, on the M branch, BChl_M is replaced by BPh_M in the corresponding position. Thus, C. aurantiacus RCs contain altogether three BPh molecules and only one BChl monomer. There exists an agreement that the primary charge separation step in purple bacterial RCs occurs with a lifetime of approx. 3 ps at room temperature. This process is slower in RCs of C. aurantiacus. We weakly decrease the electronic coupling parameters in comparison with R. sphaeroides RCs because the kinetics in this RC is slower than in R. sphaeroides RCs. To characterize C. aurantiacus, we start with the set of parameters that characterize the kinetics of WT RCs of R. sphaeroides. We assume that the free energy difference of the 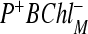state in R. sphaeroides RCs and the state of C. aurantiacus RCs is about 1,000 cm^− 1, similar to the L-branch of R. sphaeroides RCs. The values 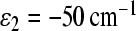and were used in our computations. The value 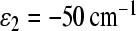is less favorable for electron transfer to the M-branch when the high-frequency modes 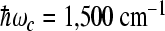are used. The following values of input parameters were used: scaled reorganization constants S_mij = 10, S_cij = 0.5, high-frequency modes  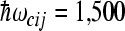cm^− 1, and low-frequency mode  cm^− 1, where i,j = 1,3,5 for the L-side and i,j = 1,2,4 for the M-side of RC. The values for electronic coupling parameters V₂₄ = V₃₅ = 32 cm^− 1 and V₁₂ = V₁₃ = 15 cm^− 1 were used. 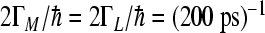The sink parameters , were used in accordance with experimental observation, which characterizes the ET to quinone molecules and decay to the ground state. The value 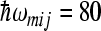 cm^− 1 for low-frequency medium mode was chosen in accordance with results of the work [26]. The value S_mij = 10 of the scaled reorganization energy constant was used to obtain the reorganization energy of medium mode  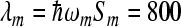cm^− 1. Since BChl_M is replaced by BPh_M in the corresponding position, we decrease the free energy in site 2. The calculated rate constants and quantum yields for the concrete energy levels are collected in Table 1, upper part.

Table 1.

Computed constants 1/k_ij and quantum yield dependence on temperature for C. aurantiacus RCs

Sample	T K	ε2 cm − 1a	ε3 cm − 1	ε4 cm − 1	ε5 cm − 1	1/k12 ps	1/k21 ps	1/k13 ps	1/k31 ps	1/k24 ps	1/k42 ps	ΦG	ΦM	ΦL
C. aurant.	295	−50	−450	−1,000	−2,000	12	15	6	52	2	188	0.02	0.31	0.67
V12 = V13	200					15	21	5	138	2	1,559	0.02	0.25	0.73
C. aurant.	295	−650	−450	−1,000	−2,000	9.1	217	11	96	2.7	14.6	0.03	0.49	0.48
V12 = V13	200					7.7	826	9.6	246	2.5	31	0.02	0.54	0.44
C. aurant.	295	−50	−450	−1,000	−2,000	47	60	11	93	2	188	0.05	0.16	0.79
V12 ≠ V13	200					58	84	10	246	2	1,559	0.05	0.12	0.83

The constants 1/k₃₅ = 3(3.8) ps and  ps for T = 295(200)K

We can see that, in this case, we get electron transfer through the M branch, which is not in accordance with experimental observations. To avoid this discrepancy, we must assume that asymmetry in the electronic coupling exists. To describe the experimental kinetics for the C. aurantiacus RC, we used the following asymmetry in electronic couplings: V₁₂ = 10 cm^− 1 and V₁₃ = 15 cm^− 1. We used the energy ε₂ = − 50 cm^− 1 in the calculation because this case is less favorable for electron transfer through the M-branch, and so needs less asymmetry in the electronic coupling to achieve agreement with experimental data.

The calculated rate constants and quantum yields for the concrete energy levels are shown in Table 1, bottom part. The solution of Eq. 4 can be expressed in the form (T = 295K)

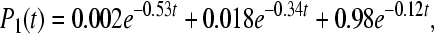9a

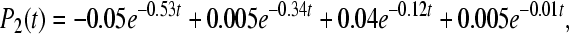9b

9c

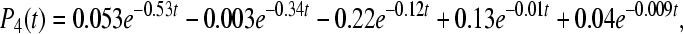9d

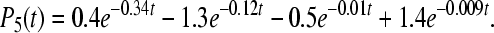9e

The behavior of the occupation probabilities P_i(t) at 295K is shown in Fig. 2. Similar to the work [18], we describe the kinetics with five exponential components. In our case, it is because the five-site model was used.

Fig. 2.

The occupation probabilities P(t) for C. aurantiacus RC in the asymmetric case V₁₂ = 10 cm^− 1 and V₁₃ = 15 cm^− 1

Rhodobacter sphaeroidesH(M182)L reaction center

In this mutant, BChl_M is replaced with BPh_M. The new cofactor is referred to as ϕ_B. The new state 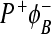is formed during the decay of P ^* and recombines to the ground state with a lifetime of 200 ps. The yield of is about 0.35 at room temperature and the yield of is about 0.65. There does not appear to be any further electron transfer from ϕ_B to BPh_M. The yield of the state decreases to 0.12 at 77 and 9K. It is thought that, in the H(M182)L mutant, the 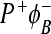state is lower in energy than 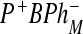[27, 28].

To elucidate the electron kinetics in this RC, we test two models. The first model is a coherent model where we assume that the free energies of the and states are closely spaced and the reorganization energy is practically zero when an electron is transferred between these two states. The second model is an incoherent model where the free energy of the state is substantially below 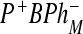. Both models predict a small probability of finding electron at site 4. The following values of input parameters were used: scaled reorganization constants S_mij = 10, S_cij = 0.5, high-frequency mode  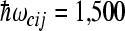cm^− 1, low-frequency mode  cm^− 1 where i,j = 1,3,5 for theL-side and i,j = 1,2,4 for theM-side of RC. The values for electronic coupling parameters V₂₄ = V₃₅ = 59 cm^− 1,V₁₂ = V₁₃ = 32 cm^− 1 were used. 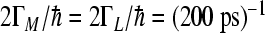The sink parameters , were used in accordance with experimental observation, which characterizes the ET to quinone molecules and decay to the ground state.

To explain the electron transfer in this mutant, we started with the coherent model. This means that we assume that the reorganization energy for ET from the 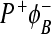state to is practically zero. The electron kinetics has to be described by the following system of equations:

10a

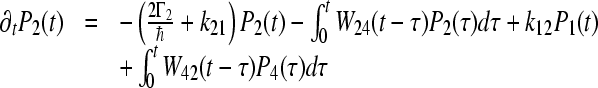10b

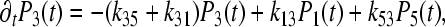10c

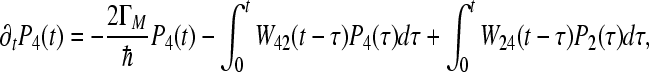10d

10e

In this case, the memory function W₂₄ = W₄₂ can be expressed in the form: , we begin with the assumption that Γ₂ = 0. This means that recombination to the ground state from site 2 does not exist. The calculated values of parameters for the coherent model, which describes the mutant RCs, are collected in Table 2, upper part. As can be seen, there is very small decay to the ground state. To fit the experimental data of the mutant RCs, we need to introduce the possibility of a recombination of the state directly into the ground state. So we also include sink Γ₂ ≠ 0 into Eq. 10, where . The computed rate constants and quantum yields after this assumption are shown in the bottom part of Table 2. In this case, the occupation probabilities P_i(t) at 295K can be expressed in the form:

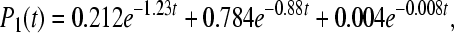11a

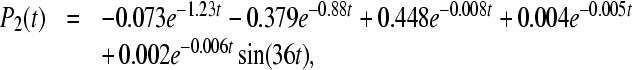11b

11c

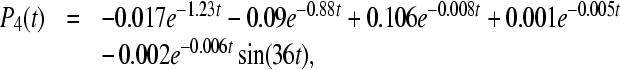11d

11e

We can see in this case that occupation probabilities P₃(t) and P₄(t) have an oscillating character. The frequency of oscillations depends on the free energy difference and electronic coupling parameter between these two sites [29]. The electron transfer kinetics for coherent models are shown in Fig. 3.

Table 2.

Computed constants 1/k_ij and quantum yield dependence on temperature for R. sphaeroidesH(M182)L mutant RCs

Coherent sample	T K	ε2 cm − 1	ε3 cm − 1	ε4 cm − 1	ε5 cm − 1	1/k12 cm − 1	1/k21 ps	1/k13 ps	1/k31 ps	1/k24 ps	1/k42 ps	ΦG	ΦM	ΦL
	295	−850	−450	−1,000	−2,000	1.9	121	2.4	21	1,293	1,293	0.01	0.09	0.90
Γ2 = 0	200					1.6	729	2.1	54	1,293	1,293	0.01	0.30	0.69
	77					1.1	106	1.9	8,479	1,293	1,293	0.004	0.628	0.368
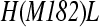	295	−850	−450	−1,000	−2,000	1.9	121	2.4	21	646	646	0.29	0.07	0.64
Γ2 ≠ 0	200					1.6	729	2.1	54	646	646	0.43	0.10	0.47
	77					1.1	106	1.9	8,479	646	646	0.51	0.12	0.37

The constants 1/k₃₅ = 0.9(1.1)(3.3) ps and 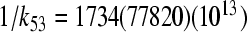 ps for T = 295(200)(77)K,

Fig. 3.

The occupation probabilities P(t) for the mutant H(M182)L in the case of the coherent model of electron transfer where , T  =  295K

Now we intend to elucidate the observed ET kinetics with incoherent models. The value of the free energies used to calculate the rate constant are listed in Table 3. It was assumed that the free energy of is significantly below because of the electron transfer stops at ϕ_B [27, 30]. In the case Γ₂ = 0, we get a very small probability of finding an electron on the BPh_M molecule, but the quantum yield through the branch M is substantial (Table 3, upper part). So we have to impose, as in the previous case, the possibility that the 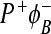state can recombine directly into a ground state. The value was used. The computed rate constants and quantum yields after this assumption are collected in the bottom part of Table 3. We found the following expressions for the occupation probabilities P_i(t) for an incoherent model at 295K in this case:

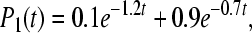12a

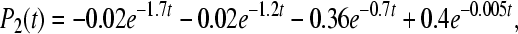12b

12c

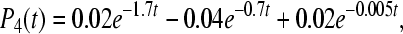12d

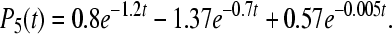12e

The time dependence of the site-occupation probabilities P_i(t) for an incoherent model is presented in Fig. 4.

Table 3.

Computed constants 1/k_ij and quantum yield dependence on temperature for R. sphaeroidesH(M182)L mutant RCs

Incoherent sample	T K	ε2 cm − 1	ε3 cm − 1	ε4 cm − 1	ε5 cm − 1	1/k12 ps	1/k21 ps	1/k13 ps	1/k31 ps	1/k24 ps	1/k42 ps	ΦG	ΦM	ΦL
	295	−1,600	−450	−1,000	−2,000	3.2	7,797	2.4	21	11	0.6	0.01	0.34	0.65
Γ2 = 0	200					3.9	398,011	2.1	54	39	0.5	0.01	0.33	0.66
	77					12	1014	1.9	8,479	27,477	0.37	0.01	0.13	0.86
	295	−1,600	−450	−1,000	−2,000	3.2	7,797	2.4	21	11	0.6	0.42	0.02	0.56
Γ2 ≠ 0	200					3.9	398,011	2.1	54	39	0.5	0.35	0.01	0.64
	77					12	1014	1.9	8,479	27,477	0.37	0.14	0	0.86
	9					4.9	10111	0.68	1031	1041	0.38	0.125	0	0.875

The rate constants 1/k₃₅ = 0.9(1.1)(3.3)(3.11) ps and 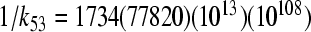 ps for T = 295(200)(77)(9)K,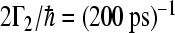

Fig. 4.

The occupation probabilities P(t) for the H(M182)L mutant in the case of the incoherent model of electron transfer where , T = 295K

The system deactivates to the ground state mainly through the state. To get the quantum yields in accordance with experimental data, we have to use the value S_mij = 5 at T = 9K.

Conclusion

We have dealt with electron transfer in C. aurantiacus and R. sphaeroidesH(M182)L mutant RCs. In spite of their structural similarity, their functionality is very different. The H(M182)L mutant reveals the M-branch active in electron transfer.

Discussions about the main factors determining electron transfer directionality can be found in the papers [26, 31–34]. Previously, it was suggested that the difference in the electronic coupling parameters in the two branches is the dominant factor. Later, experimental work cast doubt on the dominance of electronic coupling as a mechanism that causes the asymmetry in ET through branches [27, 30]. Our position is that the parameters describing electron transfer from the bacteriochlorophyll dimer to bacteriochlorophyll monomers are crucial for unidirectionality. Obviously, mutations in RCs with a goal to change these parameters can identify what the most important parameter for unidirectionality is.

In RCs, electron transfer is sensitive to the free energy difference between the charge-separated states. In the case of C. aurantiacus RCs, we assume that the free energy of the state at site 2 is in the range of 1,000 cm^− 1 below the 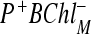state at site 2 of R. sphaeroides RCs. It is estimated that this energy is about 800 cm^− 1 above P ^* in R. sphaeroides RCs [35]. We have examined two possible values of the free energy of the state at site 2, 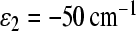and 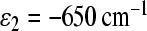. The value is less favorable for electron transfer through the M-branch. In both cases, the M-branch is active. So we have to introduce coupling integrals asymmetry with to get accordance with the experimental data.

In the case of the R. sphaeroidesH(M182)L mutant RCs, we have investigated two possibilities. The first one has free energy of the and states closely spaced. The second one has free energy of the state 600 cm^− 1 below free energy of . In the first case, we used the model where, between the sites 2 and 4, electron transfer has a coherent character. This means that the electron is delocalized between these two sites. It was assumed that reorganization energy is small when electron is transferred from ϕ_B to the BPh_M molecule. The coherent model was used because is not clear why this mutation can decrease the free energy of the BPh (refereed as ϕ_B) molecule so substantially below the P ^* state. The incoherent model in this case gives a significant probability to find the system at the 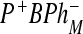state. Without assuming the possibility that the 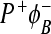state can decay directly to the ground state, the coherent model gives more realistic results then the incoherent model. But in both models, there is the outlet through the M branch, which is not in accordance with experimental observations. The problem of both the coherent and incoherent models is that they do not predict enough decay to the ground state without the assumption that there is a possibility of 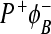state recombination to the ground state. If we take this possibility into account, both models give results in good agreement with experimental observation at 295K. The coherent model predicts an incorrect dependence of quantum yield on temperature. The coherent model does not produce results that are in accordance with experimental data in this case but can be used, for instance, when we want to investigate how the BChl dimer can contribute to electron transfer asymmetry [36]. A similar model ought to be used to characterize electron transfer in the PSII (PSI) system, where dimer molecules of BChl are not so close as in the bacterial RCs.

The incoherent model can elucidate electron transfer in R. sphaeroidesH(M182)L mutant RCs without asymmetry in electronic coupling parameters using the set of parameters that characterizes the observed L-side experimental kinetics very well [16, 17, 23]. To characterize the H(M182)L mutant, we used the value 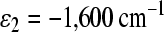for the free energy of the state. At 9K, the value S_mij = 5 has to be used to fit the experimental data. To get appropriate results at T = 9K, we have to change the reorganization energy of the low-frequency mode from the value 800 cm^− 1 to the value 400 cm^− 1. Using the value 800 cm^− 1, the yield of the state is 0.04, which is not in accordance with experimental data. The decrease of the reorganization energy at low temperature can be due to the fact that friction with the surrounding medium is greater. The result is that the configuration displacement d_mi − d_mj at low temperature is smaller than that at room temperature.

One of the unsolved problems of electron transfer in the RC is unidirectionality. The electron used only one of two possible branches. Much experimental work has been performed to solve this problem [9, 10, 27, 28, 37, 38]. Generally, it is assumed that RCs have common features and the unidirectionality is caused mainly by asymmetry in the coupling integral or asymmetry in the free energy, or that both these asymmetries contribute to unidirectionality. This paper shows that there is a possibility that different RCs can have different grounds for unidirectionality.

To derive the kinetic equations, the projection operator technique has been used. The physics depends on the concrete projection operator, which was used. If we assume that, after excitation, the electron transfer is so fast that relevant vibrational modes have no time to relax, we can average over the surrounding medium, which is in equilibrium with the dimer in the ground state and not in the excited state. The models used in the presented paper can describe such quick electron transfer.

To also describe the bath dynamics, additional free parameters are needed [39]. The theoretical model where the bath relaxation is imposed also has to fit the experimental data. The data determine a model in which phonon relaxation may or may not play an important role. If the relaxation is important, there has to be another set of parameters in the model, in which this process is taken into account in comparison with the presented model. For instance, both models give different predictions for electron transfer in experiments where the electric fields are applied. In the optimal case, a comparison with experimental data can guide the selection of a correct model, and establish a role of phonon relaxation in the electron transfer in the RCs.

To describe both the unidirectionality and the results of the experiments with mutated RCs, we used the five-site model. For this complex system, the parameters, which describe the L-side electron transfer very well, were applied. Despite a large discussion about these parameters, the key problem is, however, to determine the M-side parameters. Because of the two-fold symmetry of RCs, the L-side parameters were also used to describe the M-side electron transfer. But there must be asymmetry in some parameter to get unidirectionality of electron transfer. Our goal was to determine which parameters are critical and what are the values of these parameters. Previously, it was presumed that the asymmetry in coupling integrals results in the asymmetry of electron transfer. Several studies with mutated RCs showed that it is not a sufficient explanation. It cannot be only the asymmetry of coupling integrals, but rather the asymmetry of the free energy of bacteriochlorophyll monomers located on different branches that appears to be the key factor of unidirectionality. We believe that the presented model can identify the parameters that are changed in the mutated RC in comparison to WT and also determine the impact of mutation on the RCs. We also believe that we can identify the parameters that play a key role in the unidirectionality in the RC of C. aurantiacus. The values of these parameters are reasonable. Without their change in comparison to R. sphaeroides mutant RC, we have L-side electron transfer, which is not observable in the RC of C. aurantiacus. Generally, it was believed that asymmetry in coupling integrals or asymmetry in free energy or both these asymmetries together are the main reason for unidirectionality in bacterial RCs. We show here that there is some diversification of mechanisms among different RCs. In some RCs, the main impact on the unidirectionality comes from the asymmetry in coupling integrals (C. aurantiacus), and in others, the key factor can be the asymmetry in free energies (R. sphaeroides). Until now, such a possibility has not been taken into account, and it can be important if artificial RCs with similar performance are constructed. We utilized the rate constant, which allows us to make a prediction for electron transfer at very low temperature (9K).

It is important to compute the temperature dependence of quantum yields and also to compute the electron transfer kinetics. It can help to estimate more correctly the values of model parameters and subsequently to contribute to better understanding of the primary processes of photosynthesis.