Abstract
There is a long history of using allele sharing distance (ASD) and closely related metrics for population stratification analysis. However, the theory for this practical usage has not been reported. In this paper, we describe the theoretical background for using ASD on single nucleotide polymorphism (SNP) genetic data for human population stratification analysis. In showing the proof, we lay the ground work for a general distance-based method for classifying subpopulations using SNPs and ASD. We also show its relation to other closely related distance metrics using HapMap Phase I SNP data.
Key Words: Population stratification, Coancestry coefficient, Single nucleotide polymorphism, Allele sharing distance
Introduction
With the advent of rapid single nucleotide polymorphism (SNP) genotyping and the availability of genome-wide SNPs there is a growing need for population stratification detection methods that can take advantage of large datasets and eliminate dependency on model parameter estimations. One particularly appealing approach is using the allele sharing distance (ASD) [1], or the similar metric identity by state (IBS) [2]. It does not require allele/genotype frequency estimation, which makes it still valid when sample sizes are small. It is also suitable for population outlier detection, is robust to high linkage disequilibrium (LD) among SNPs, and can be rapidly calculated.
There is a long history of using ASD and closely related metrics (either proportion of allele sharing or IBS) for population stratification analysis [1,2,3,4,5,6,7,8]. Despite the difference in the clustering approaches employed, the pair-wise ASD distance matrix is nearly the same for all the distance-based clustering methods. It seems that the pair-wise ASD distance matrix contains sufficient information for separation and is a basis for many distance-based clustering approaches. However, to date there has not been a rigorous theoretical foundation for using ASD for human population classification.
A.W.F. Edwards [9] showed that different haploid populations can be distinguished through the half matrix of pair-wise distances between individuals, but it is not clear how the rational applies to dipoid populations. For haploid populations, at a single biallelic locus there are only two possible categories, and they can be modeled by a binomial distribution [9]. However, human populations are diploid. If we consider biallelic SNPs, then there are three possible categories for the genotypes at each locus, and a simple binomial distribution no longer applies. Does Edwards's rational still apply to diploid populations? If so, then human population stratification analysis can be greatly simplified since we can rely on the pair-wise distance matrix for the classification.
The work in this paper extends Edwards's idea [9] to diploid populations using a coancestry approach and lays the ground work for a general distance-based method for classifying subpopulations using SNPs and ASD. In this work, we derive the statistical background for using ASD on SNPs for population stratification detection using standard population genetics theory. We show that large numbers of random genome-wide SNPs provide sufficient information for accurate clustering. Diploid individuals from different subpopulations can be separated using the pair-wise distance matrix without estimation of allele frequencies.
Theory
Without loss of generality, we consider two subpopulations descended from a single reference ancestral population. Random mating is assumed within each subpopulation. The subpopulations have the same expected allele frequencies in the absence of disturbing forces, e.g. unequal selection in different subpopulations [10]. We denote θ as the probability that two alleles at a locus in the same subpopulation are identical by descent (IBD). Therefore, different alleles within a subpopulation are related to a magnitude θ. θ is also sometimes referred to as FST [11]. We assume that subpopulations have reached equilibrium so that θ is not changing over time [12].
Throughout the paper we consider only biallelic SNPs. We denote the population frequencies of alleles A1 and A2 at a locus as p1 and p2, respectively, and their values may be unknown in practice. The probability that an allele drawn from the subpopulation is of type A1 is P(A1) = p1 and similarly P(A2) = p2 for A2 and p1 + p2 = 1. Given that the coancestry coefficient between alleles at a locus is θ, the probability of observing two alleles both of type A1 is P(A1A1) = θp1 + (1 – θ)p21, and similarly P(A1A2) = 2(1 –θ)p1p2. If P(A1mA2n) is the probability of observing m copies of A1 alleles and n copies of A2 alleles in a random drawing of m + n alleles, then it can be shown [13, 14] that
| (1) |
The above formulas can also be derived through a Dirichlet approach [14,15,16] by realizing that the probability that the next allele sampled is of type Ai given that mi copies of Ai have already been found in a set of m alleles is,
| (2) |
where {pi} are the population allele frequencies.
In randomly mating subpopulations, DNA profiles are essentially samples of alleles [14, 15]. Therefore, the joint genotype probabilities for biallelic SNP markers for randomly drawn members of the same subpopulation with evolutionary relatedness can be obtained through successive implementation of equations (1) or (2) and are represented in the following series of equations:
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
where p2 = 1 – p1. The equations above already account for the different possible ordering of the genotypes and the two alleles within each genotype.
In order to quantify the distance among individuals and construct the pair-wise distance matrix, we need a distance measure. ASD, and closely related distance measures, are popular metrics in distance-based population structure analysis with a long history [1,3,4,5,6,7,8]. In this work, we chose to use ASD to construct the distance matrix between all pairs of individuals.
The ASD distance between individuals i and j is defined as
| (9) |
where
| (10) |
and L is the number of SNP loci used.
At a SNP locus, there are nine possible genotype combinations between individuals i and j. Using the following notation, a genotype before a comma is from person i and a genotype after a comma is from person j, there are three situations where d = 0, i.e., (A1A1, A1A1), (A1A2, A1A2) and (A2A2, A2A2); four where d = 1, i.e., (A1A1, A1A2), (A2A2, A1A2), (A1A2, A1A1) and (A1A2, A2A2); and two where d = 2, i.e., (A1A1, A2A2) and (A2A2, A1A1). For a given θ, we denote d as dθ. Therefore, the distribution of dθ at a locus is
| (11) |
After slightly tedious calculations, the expected value of dθ is
| (12) |
and the variance of dθ is
| (13) |
With E(dθ) and Var(dθ) derived, we can now examine the effects of different values for θ. In the simplest case the subpopulations have been isolated since the ancestral population and alleles in each subpopulation are not related to those in the other. Therefore, alleles between subpopulations are independent (θ = 0) [10]. Then
| (14) |
and
| (15) |
The expected allele sharing distance difference between individuals from different subpopulations and individuals from the same subpopulation is
| (16) |
which is >0 ∀p1 ∈ (0, 1) since p1p2 ≤ 0.25.
It is also possible that alleles in different subpopulations are related by a nonzero coancestry, e.g. when there is migration between subpopulations [10]. However, it can be shown that the partial derivative of the expected value of dθ with respect to θ is
| (17) |
which is <0 ∀p1 ∈ (0, 1) since p1p2 ≤ 0.25. Therefore, the expected value of dθijis a decreasing function over θ, which means that the expected ASD is always greater between than within subpopulations even when the coancestry between subpopulations is nonzero since the coancestry within is greater than between subpopulations. This relationship holds for all allele frequencies.
Now suppose that there are L independent SNP loci (the independent assumption is valid given the number of loci required to separate populations is much lower than the number of SNPs in the human genome), the expected value and variance of allele sharing distance D over these loci for a given θ are
| (18) |
| (19) |
It is not difficult to show that the maximum value of the variance of dθ is 0.4375. Therefore, the variance of D decreases as more SNPs are used because Var(dθl) has the upper bound 0.4375 and L2 increases much faster than the increase of ΣLl= 1Var(dθl), Var(D) → 0 as L → ∞. Increasing the number of SNP loci used makes it more apparent that there are significant ASD differences between subpopulations, as compared with the differences within subpopulations, and the expectation of D between individuals from the same subpopulation will hardly overlap with individuals from different subpopulations. Therefore it is possible to differentiate subpopulations from the half-matrix of pair-wise distances without explicitly estimating allele frequencies for each subpopulation. The population stratification problem is thus reduced to contrasting the ASD means of different groups. It is through the accumulated effect of many SNP loci and the coancestry among individuals within subpopulations that population stratification can be identified.
Numerical Examples
Given the ASD properties that we have just derived, we can use numerical examples to explore it. Specifically, for a given coancestry coefficient we can determine the number of SNPs required to separate subpopulations. In calculating the variance of ASD, we will use the upper bound of variance (0.4375) for all SNP loci. Thus, Var(D) ≈ 0.4375/L. This approach of variance approximation is simple, though slightly conservative. In order for the expected ASD of between (E(Dθb)) and within subpopulations (E(Dθw)) to be x standard deviations apart, i.e. , the L has to be at least x2 0.4375/(E(Dθb) – E(Dθw))2. Also, while allele frequencies are discrete in nature, it is reasonable to approximate them as continuous values [17,18,19]. Therefore, we model the distribution of allele frequencies by two kinds of distributions: Uniform and Beta.
In the first example we consider p1 as the minor allele frequency (MAF) and model it by a Uniform [0.1, 0.5] distribution (consider only common SNPs). This approximation is reasonable, though biased given the distribution of allele frequencies for genome-wide autosomal SNPs appear to be ‘flat’ in the Hapmap Phase I dataset under predisposed ascertainment [20]. If we treat E(dθ) as a function of p1 and denote f(p1) = E(dθ), the expected ASD between individuals can be derived as
Suppose θ = 0.15 and θ = 0 for individuals within subpopulations and between subpopulations, then the corresponding values for E(D) are 0.534 and 0.623, respectively. For a set of 497 independent loci, the means ± SD are 0.534 ± 0.03 and 0.623 ± 0.03. Thus, the difference between means, 0.089, is about 3 SD away. In cases when alleles in different subpopulations are related by a nonzero coancestry, we assume θ = 0.05, and thus, E(D) = 0.593. For a set of 1,131 independent loci, the means ± SD for individuals within subpopulations and between subpopulations are 0.534 ± 0.020 and 0.593 ± 0.020, respectively. Thus, the difference between means, 0.059, is about 3 SD away. This demonstrates that it requires more SNP loci to reach similar separation between ASD means when different subpopulations are related by a nonzero coancestry. With enough SNP loci, the entries of the triangular-matrix of pair-wise distances will divide into two separate groups with hardly any overlap.
In the second example we adopt Wright's two-state mutation model [18] for the stationary pdf of allele frequencies, q, as
where N is the effective population size, v is the mutation rate from allele a to A and rate u for A to a and Γ() denotes the gamma function. Assuming N is 106 and the SNP mutation rate equals 10–8, we approximate MAF as a Beta(0.04, 0.04) distribution (4 × 106 × 10–8 = 0.04). Again, we only consider common SNPs with MAF ∈ [0.1, 0.5]. As shown in the previous example, we can derive the E(D) by integration for θ = 0.15 and θ = 0 and get the corresponding means of ASD as 0.500 and 0.587, respectively. For a set of 520 independent loci, the means ± SD are 0.500 ± 0.029 and 0.587 ± 0.029, respectively. Thus, the difference between means, 0.087, is about 3 SD away. When alleles in different subpopulations are related by a nonzero coancestry, we assume θ = 0.05, and thus, E(D) = 0.557. For a set of 1,212 independent loci, the means ± SD for individuals within subpopulations and between subpopulations are 0.500 ± 0.019 and 0.557 ± 0.019. Thus, the difference between means, 0.057, is then about 3 SD away. Again, we see that with enough SNP loci, the entries of the triangular-matrix of pair-wise distances will divide into two separate groups with hardly any overlap. Individuals from different subpopulations are separable based on the ASD matrix without having to calculate the allele frequencies.
Relation to Other Work
Recently, principal component analysis (PCA)-based approaches were proposed to address population stratification issues [21, 22], which use covariance among normalized genotype scores of individuals. ASD and the covariance-based approaches are similar in nature. In the ASD-based approaches, individuals with small ASD tend to cluster together. While in PCA-based approaches, large eigenvalues (nonrandom population stratification) are consequences of high correlation among vectors of genotype scores. Intuitively, small ASD among individuals will correspond to high correlation among genotype vectors. Both small ASD and high correlation should be due to the result of evolutionary relatedness, coancestry, which can be captured by genome-wide random SNPs.
While ASD and correlation-based methods are related, they lend themselves to different types of analysis and this makes it difficult to make a definitive statement about the superiority of one method over another. Depending on the starting matrix, different ordination or clustering methods can be used to inspect the ethnic relationship among individuals. If a dissimilarity matrix like ASD is used, multidimensional scaling (MDS) and Ward's minimum variance method can be used [1, 2, 23]. If the starting matrix is a correlation matrix, PCA can be used instead [21, 22] as well as MDS.
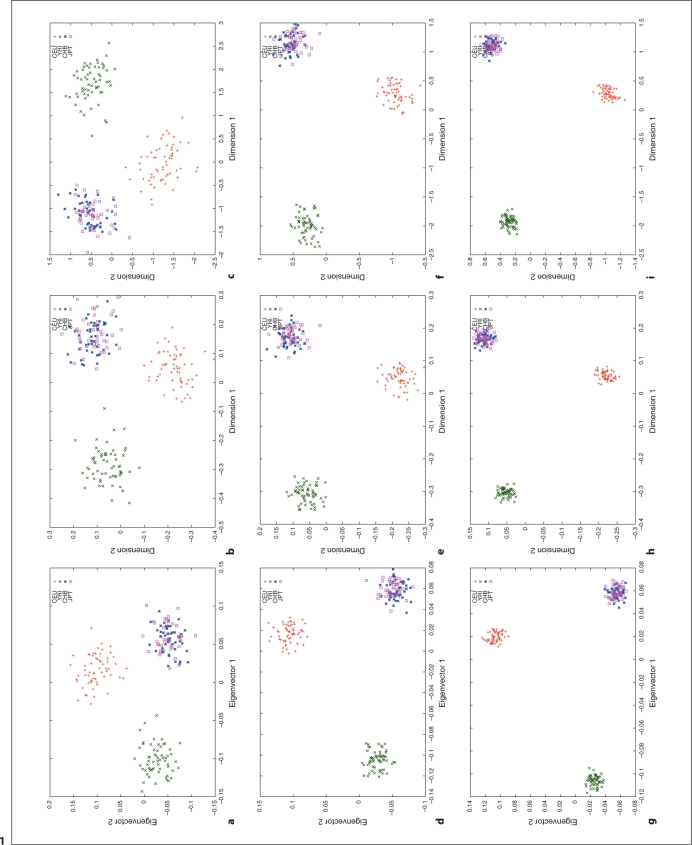
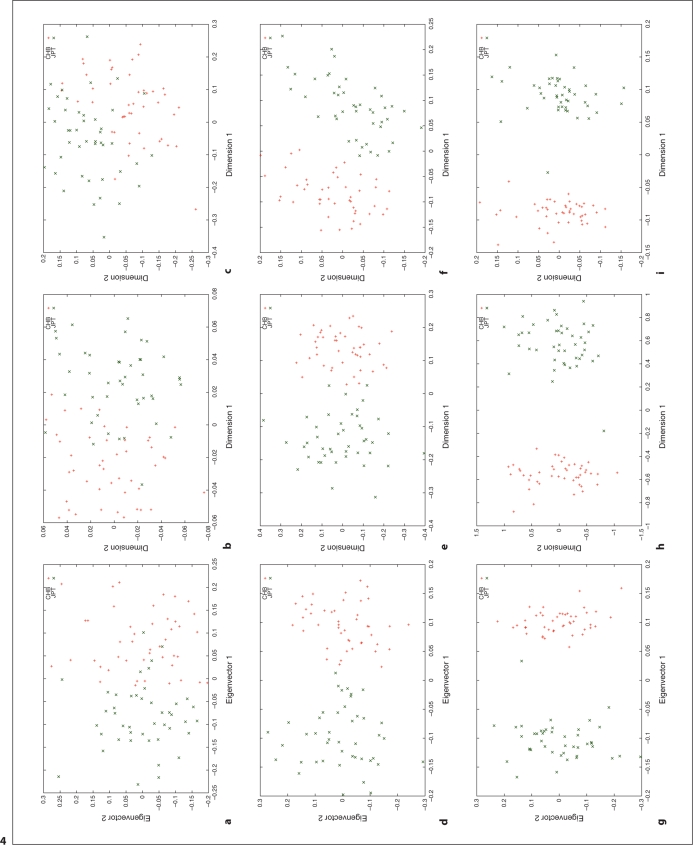
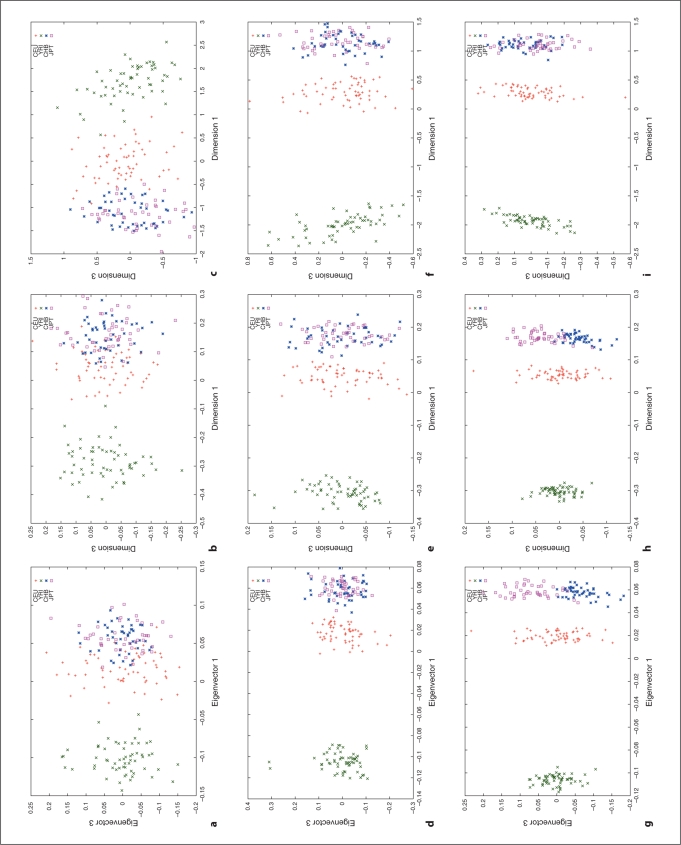
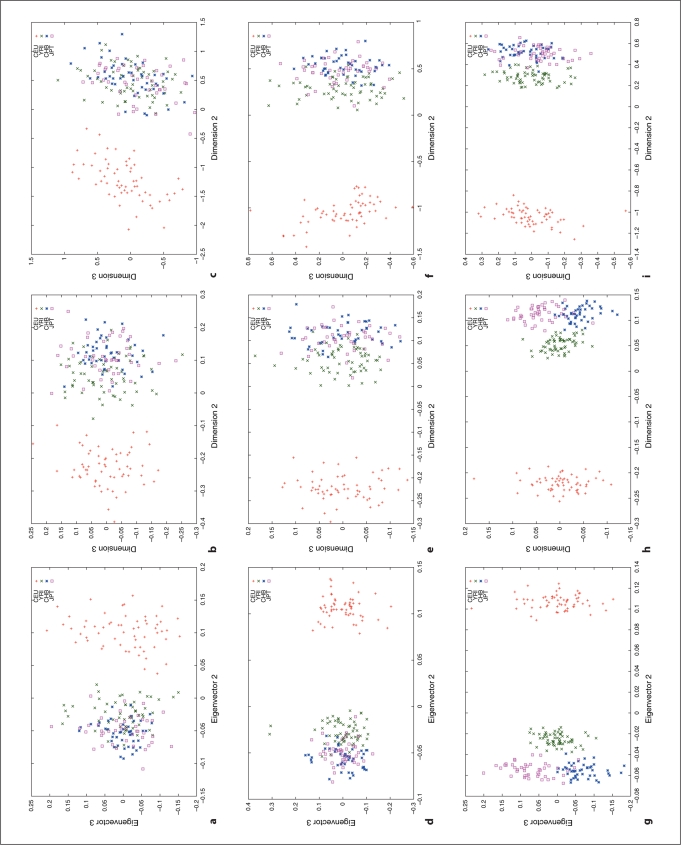
We used HapMap Phase I SNP data [20, 24] to explore the relation between different distance metrics, i.e. ASD vs. correlation/covariance, using corresponding clustering methods, MDS as implemented in R (http://www.r-project.org/) and PCA as implemented in the software, EigenSoft (http://genepath.med.harvard.edu/reich/Software.htm). In the HapMap Phase I SNP data, about 1.1 million SNPs were genotyped genome-wide in 269 individuals from four ethnic populations: Yoruba in Ibadan (YRI), CEPH in Utah residents with ancestry from northern and western Europe (CEU), Han Chinese from Beijing, China (CHB), and Japanese from Tokyo, Japan (JPT), among which there are 209 unrelated individuals: 60 CEU, 60 YRI, 45 CHB and 44 JPT. For this study, we only used unrelated individuals and genomewide random autosomal SNPs. The cluster results are plotted in figures 1–4. Figures 1, 2 and 3 show the clustering results (Dimension 1 vs. 2, Dimension 1 vs. 3 and Dimension 2 vs. 3, respectively) for the CEU, YRI and CHB + JPT individuals using different distance metrics and clustering methods with a number of genome-wide autosomal SNP loci. 100, 500 and 2,000 SNPs are used in the top, middle and bottom panel, respectively. Figure 4 shows the clustering results for the CHB and JPT individuals using different distance metrics and clustering methods with a number of genome-wide autosomal SNP loci. 1,000, 5,000 and 20,000 SNPs are used in the top, middle and bottom panel, respectively. In figures 1–4, clusters in the left, middle and right column are generated using the covariance matrix and PCA, the ASD matrix and MDS, the correlation matrix and MDS, respectively.
Fig. 1.
Cluster results for the CEU, YRI and CHB + JPT individuals (Dimension 1 vs. 2). This figure shows the clustering results using different distance metrics and clustering methods with a number of genome-wide random autosomal SNP loci. In the left column, (a), (d) and (g) correspond to the clusters generated using the covariance matrix and PCA. In the middle column, (b), (e) and (h) correspond to the clusters generated using the ASD matrix and MDS. In the right column, (c), (f) and (i) correspond to the clusters generated using the correlation matrix and MDS. In the top row, (a), (b) and (c), 100 SNPs are used. In the middle row, (d), (e) and (f), 500 SNPs are used. In the bottom row, (g), (h) and (i), 2,000 SNPs are used. Abbreviation: SNP, single nucleotide polymorphism; PCA, principal component analysis; ASD, allele sharing distance; MDS, multidimensional scaling.
Fig. 4.
Cluster results for the CHB and JPT individuals. This figure shows the clustering results using different distance metrics and clustering methods with a number of genome-wide random autosomal SNP loci. In the left column, (a), (d) and (g) correspond to the clusters generated using the covariance matrix and PCA. In the middle column, (b), (e) and (h) correspond to the clusters generated using the ASD matrix and MDS. In the right column, (c), (f) and (i) correspond to the clusters generated using the correlation matrix and MDS. In the top row, (a), (b) and (c), 1000 SNPs are used. In the middle row, (d), (e) and (f), 5,000 SNPs are used. In the bottom row, (g), (h) and (i), 20,000 SNPs are used. Abbreviation: SNP = single nucleotide polymorphism; PCA = principal component analysis; ASD = allele sharing distance; MDS = multidimensional scaling.
Fig. 2.
Cluster results for the CEU, YRI and CHB + JPT individuals (Dimension 1 vs. 3). The figure legend is the same as that in figure 1.
Fig. 3.
Cluster results for the CEU, YRI and CHB + JPT individuals (Dimension 2 vs. 3). The figure legend is the same as that in fig ure 1.
Figures 1–4 show the same pattern: with the increasing number of SNPs used, the within subpopulation individuals are closer and closer to each other while the between subpopulation individuals are farther and farther away from each other. Moreover, different distance metrics, ASD and correlation/covariance, with different clustering methods, MDS and PCA, identified very similar clusters in these data sets except that covariance + PCA and ASD + MDS showed better separation on CHB and JPT individuals than correlation + MDS did when enough SNPs were used, e.g. 2000 SNPs, in figures 2 and 3 g and h versus i. Multiple runs also gave similar results (data not shown).
Discussion
The importance of this work is to provide theoretical support for the observation that human populations can be separated simply through a pair-wise distance matrix, which has been shown in a large empirical study using Hapmap [20, 24] and Perlegen [25] SNP data sets [1]. Moreover, through the derivation of the distance method, the population stratification problem is reduced to contrasting the means of different clusters. We focus on explaining why ASD works in population stratification analysis rather than how to cluster genetic data using ASD. Based on the ASD matrix, standard statistical clustering algorithms, e.g. Ward's minimum variance and MDS methods, can be used to further inspect the ethnic relationship among individuals. We concentrate on biallelic SNPs in this study. The multiallelic genetic markers, microsatellites, are also effective in human evolutionary studies using the pairwise distance matrix of proportion of allele sharing [3] and should follow similar reasons: individuals within subpopulations have a higher proportion of allele sharing than between subpopulations since the match probabilities within is greater than between subpopulations due to coancestry.
From the ASD derivation, we see that when sufficient SNP loci are used in the analysis, the distribution of within-subpopulation ASD and between-subpopulation ASD hardly overlap with each other and the subpopulations are separable. One of the advantages of the distance method is that there is no need to specify the allele frequencies explicitly. Therefore, population allele frequencies do not have to be approximated by sample allele frequencies. This is important because sample allele frequencies may give biased results due to high variability. The allele frequencies and coancestry information are embedded in the pair-wise distance matrix over a large number of random SNP loci. In contrast, model-based methods, like, STRUCTURE [26] and L-POP [27], which use sample allele frequencies as surrogates for subpopulation allele frequencies, need relatively large data sets for each subpopulation in order to estimate allele frequencies reliably, which may not be feasible in practice. Another advantage of the distance method is it is easy to calculate with no decrease in accuracy and is also suitable for population outlier detection (it is unlikely to know the allele frequencies for the outlier individuals).
In summary, we have shown the theoretical foundation for using ASD for human population stratification analysis. The ASD method combined with SNP markers have considerable power in population stratification analysis and it is not necessary to estimate allele frequencies to separate individuals with different ethnic backgrounds. The correlation/coancestry among individuals within subpopulations, which can be captured by the ASD, contributes to the classification. Diploid individuals from different subpopulations can thus be separated from half-matrix of pair-wise distances.
Acknowledgements
This work was supported in part by NIH grants R01HL08770002S1, U01AG02374605, GM45344 and NS39764. Dr. Bruce Weir provided initial guidance for population genetics theory. Dr. Joshua Starmer gave advice in manuscript preparation. We thank anonymous reviewers for providing constructive feedback for this work.
References
- 1.Gao X, Starmer J. Human population structure detection via multilocus genotype clustering. BMC Genet. 2007;8:34. doi: 10.1186/1471-2156-8-34. doi:10.1186/1471-2156-8-34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira MA, Bender D, Maller J, Sklar P, de Bakker PI, Daly MJ, Sham PC. Plink: A tool set for whole-genome association and population-based linkage analyses. Am J Hum Genet. 2007;81:559–575. doi: 10.1086/519795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bowcock A, Ruiz-Linares A, Tomfohrde J, Minch E, Kidd J, Cavalli-Sforza L. High resolution of human evolutionary trees with polymorphic microsatellites. Nature. 1994;368:455–457. doi: 10.1038/368455a0. [DOI] [PubMed] [Google Scholar]
- 4.Mountain J, Cavalli-Sforza L. Multilocus genotypes, a tree of individuals, and human evolutionary history. Am J Hum Genet. 1997;61:705–718. doi: 10.1086/515510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Nakamura T, Shoji A, Fujisawa H, Kamatani N. Cluster analysis and association study of structured multilocus genotype data. J Hum Genet. 2005;50:53–61. doi: 10.1007/s10038-004-0220-x. [DOI] [PubMed] [Google Scholar]
- 6.Shriver M, Kennedy G, Parra E, Lawson H, Sonpar V, Huang J, Akey J, Jones K. The genomic distribution of population substructure in four populations using 8,525 autosomal snps. Hum Genomics. 2004;1:274–286. doi: 10.1186/1479-7364-1-4-274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Shriver MD, Mei R, Parra EJ, Sonpar V, Halder I, Tishkoff SA, Schurr TG, Zhadanov SI, Osipova LP, Brutsaert TD, Friedlaender J, Jorde LB, Watkins WS, Bamshad MJ, Gutierrez G, Loi H, Matsuzaki H, Kittles RA, Argyropoulos G, Fernandez JR, Akey JM, Jones KW. Large-scale snp analysis reveals clustered and continuous patterns of human genetic variation. Hum Genomics. 2005;2:8189. doi: 10.1186/1479-7364-2-2-81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bauchet M, McEvoy B, Pearson LN, Quillen EE, Sarkisian T, Hovhannesyan K, Deka R, Bradley DG, Shriver MD. Measuring European population stratification with microarray genotype data. Am J Hum Genet. 2007;80:948–956. doi: 10.1086/513477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Edwards AWF. Human genetic diversity: Lewontin's fallacy. BioEssays. 2003;25:798–801. doi: 10.1002/bies.10315. [DOI] [PubMed] [Google Scholar]
- 10.Weir BS. Genetic Data Analysis II. ed 2. MA, USA: Sinauer Associates Inc.; 1996. [Google Scholar]
- 11.Weir BS, Hill WG. Estimating F-statistics. Annu Rev Genet. 2002;36:721–750. doi: 10.1146/annurev.genet.36.050802.093940. [DOI] [PubMed] [Google Scholar]
- 12.Anderson AD, Weir BS. A maximum-likelihood method for the estimation of pairwise relatedness in structured populations. Genetics. 2007;176:421–440. doi: 10.1534/genetics.106.063149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Balding DJ, Nichols RA. DNA profile match probability calculation: how to allow for population stratification, relatedness, database selection and single bands. Forensic Sci Int. 1994;64:125–140. doi: 10.1016/0379-0738(94)90222-4. [DOI] [PubMed] [Google Scholar]
- 14.Balding DJ, Nichols RA. A method for quantifying differentiation between populations at multi-allelic loci and its implications for investigating identity and paternity. Genetica. 1995;96:3–12. doi: 10.1007/BF01441146. [DOI] [PubMed] [Google Scholar]
- 15.Ayres KL. Relatedness testing in subdivided populations. Forensic Sci Int. 2000;114:107–115. doi: 10.1016/s0379-0738(00)00289-9. [DOI] [PubMed] [Google Scholar]
- 16.Weir BS, Anderson AD, Hepler AB. Genetic relatedness analysis: modern data and new challenges. Nat Rev Genet. 2006;7:771–780. doi: 10.1038/nrg1960. [DOI] [PubMed] [Google Scholar]
- 17.Fisher RA. The Genetical Theory of Natural Selection. Oxford, UK: Oxford University Press; 1930. [Google Scholar]
- 18.Wright S. Evolution in medelian populations. Genetics. 1931;16:97–159. doi: 10.1093/genetics/16.2.97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kimura M. Solution of a process of random genetic drift with a continuous model. Proc Natl Acad Sci USA. 1955;41:144–150. doi: 10.1073/pnas.41.3.144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.The international HapMap consortium A haplotype map of the human genome. Nature. 2005;437:1299–1320. doi: 10.1038/nature04226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Patterson N, Price AL, Reich D. Population structure and eigenanalysis. PLoS Genetics. 2006;2:e190. doi: 10.1371/journal.pgen.0020190. doi:10.1371/journal.pgen. 0020190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Price AL, Patterson NJ, Plenge RM, Weinblatt ME, Shadick NA, Reich D. Principal components analysis corrects for stratification in genome-wide association studies. Nat Genet. 2006;38:904–909. doi: 10.1038/ng1847. [DOI] [PubMed] [Google Scholar]
- 23.Gao X, Starmer J. AWclust: point-and-click software for non-parametric population structure analysis. BMC Bioinformatics. 2008;9:77. doi: 10.1186/1471-2105-9-77. doi:10.1186/1471-2105-9-77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.The international HapMap consortium The international HapMap project. Nature. 2003;426:789–796. doi: 10.1038/nature02168. [DOI] [PubMed] [Google Scholar]
- 25.Hinds D, Stuve L, Nilsen G, Halperin E, Eskin E, Ballinger D, Frazer K, Cox D. Whole genome patterns of common DNA variation in three human populations. Science. 2005;307:1072–1079. doi: 10.1126/science.1105436. [DOI] [PubMed] [Google Scholar]
- 26.Pritchard JK, Stephens M, Donelly P. Inference of population structure using multilocus genotype data. Am J Hum Genet. 2000;67:945–959. doi: 10.1093/genetics/155.2.945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Purcell S, Sham P. Properties of structured association approaches to detecting population stratification. Hum Hered. 2004;58:93–107. doi: 10.1159/000083030. [DOI] [PubMed] [Google Scholar]