Abstract
Species abundance distributions (SADs) are widely used as a tool for summarizing ecological communities but may have different shapes, depending on the currency used to measure species importance. We develop a simple plotting method that links SADs in the alternative currencies of numerical abundance and biomass and is underpinned by testable predictions about how organisms occupy physical space. When log numerical abundance is plotted against log biomass, the species lie within an approximately triangular region. Simple energetic and sampling constraints explain the triangular form. The dispersion of species within this triangle is the key to understanding why SADs of numerical abundance and biomass can differ. Given regular or random species dispersion, we can predict the shape of the SAD for both currencies under a variety of sampling regimes. We argue that this dispersion pattern will lie between regular and random for the following reasons. First, regular dispersion patterns will result if communities are comprised groups of organisms that use different components of the physical space (e.g. open water, the sea bed surface or rock crevices in a marine fish assemblage), and if the abundance of species in each of these spatial guilds is linked to the way individuals of varying size use the habitat. Second, temporal variation in abundance and sampling error will tend to randomize this regular pattern. Data from two intensively studied marine ecosystems offer empirical support for these predictions. Our approach also has application in environmental monitoring and the recognition of anthropogenic disturbance, which may change the shape of the triangular region by, for example, the loss of large body size top predators that occur at low abundance.
Keywords: species abundance, biomass, community structure, relative abundance, species abundance distribution, guilds
1. Introduction
Species abundance distributions (SADs) summarize a universal feature of ecological communities; all communities have a few common and many rare species. However, while this pattern of commonness and rarity is so pervasive that it has been dubbed as a law of ecology (McGill et al. 2007), it is also a pattern that defies easy explanation (Wilson & Lundberg 2004). Over 40 hypotheses (Magurran 2004; McGill et al. 2007), including both statistical (Preston 1948) and biological (Sugihara 1980) models, have been proposed in the 75 years since Motomura (1932) suggested that the geometric series could be used to explain species abundances. The challenge is not simply to replicate mathematically the SADs seen in nature, which many of the existing models do, albeit on the basis of different and sometimes incompatible assumptions, but to make distinct and testable predictions (McGill et al. 2007).
One aspect of SADs that is beginning to attract attention, and which has the potential to shed light on the underlying mechanisms, is the relationship between the shape of the distribution and the currency used to measure species importance (Morlon et al. 2009). The measure of abundance is far from trivial as it can influence the shape of SADs (Thibault et al. 2004). For example, SADs of fishes and coral are lognormal at local scales if biomass is used, and it is only at large geographical scales that a lognormal distribution of individuals becomes apparent (Connolly et al. 2005). Abundance is usually expressed as numerical abundance (number of individuals) because this is the currency in which the taxa (e.g. birds and trees) that predominate in such analyses are typically recorded. Biomass is an alternative preferred by some ecologists (Magurran 2004; Saint-Germain et al. 2007) as it is assumed to provide a more direct measure of resource use; energy flow is correlated to the body mass of individuals as metabolism scales with body mass to the 0.75 power (Kleiber 1962; Brown et al. 2004). There has been much debate about whether numerical abundance and biomass provide equivalent insights into the way in which species subdivide resources (Sugihara 1989; Pagel et al. 1991; Taper & Marquet 1996; White et al. 2004). Recently Morlon et al. (2009) used probability theory to explore the linkages between SADs constructed using different currencies and concluded that the shape of the distribution is not generally conserved during conversion from one measure of species importance to another.
Here, we draw on niche theory to link the SADs generated by alternative currencies—biomass and numerical abundance—and predict the circumstances under which the two distributions will be similar. We focus on local scales (where community processes such as competition are likely to be important) and on well-sampled communities (so that sampling effects, which can have a large influence on the perceived shape of the abundance distribution, are minimized). We also examine discrete time periods to avoid the confounding effects of autocorrelation (McGill 2003) and turnover (Magurran & Henderson 2003).
2. Theoretical basis of the biomass–numerical abundance conversion
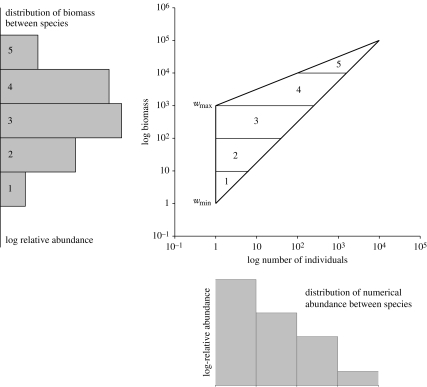
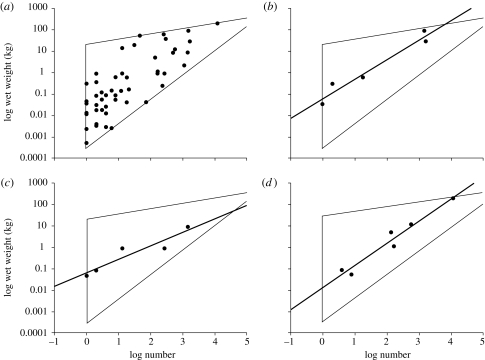
When species data for a single community are simultaneously quantified using biomass, M, and number, N, a log–log scatter plot of the two abundances will be constrained within an approximately triangular-shaped region (figure 1). The vertical side of this triangle is defined by the range of body mass for singleton species. For many communities, this range extends over several orders of magnitude. The minimum point for this line, wmin, is the minimum biomass of a single individual retained by the sampling method. This may, for example, be determined by the mesh size of the net or sieve, or limited by the particular taxonomic group under investigation. For instance, if birds or fishes were the subject of study, wmin would typically be about 1 g. The maximum, wmax, is the weight of the largest singleton species within the area of study.
Figure 1.
The derivation of the shape of the SAD in terms of biomass and number based on the assumption that the distribution of species within natural communities are scattered at random or are regularly distributed within a triangular region. In this example, we assume an obtuse triangle, which is probably the commonest pattern in well-sampled communities. wmin is the minimum biomass of a single individual retained by the sampling method. wmax is the weight of the largest singleton species within the area of study. The figure shows how the shape of the SAD can be predicted. The areas within the triangle marked 1–5 give the relative frequency of species within each log biomass size class and are plotted as a histogram to the left. The same analysis can be undertaken perpendicular to the x-axis to predict the SAD using numerical abundance.
The other two sides reflect the maximum and minimum increase in total biomass per species with numerical abundance. The lower bound tracks increasing total biomass, Mi, for populations of size, N, comprising individuals which on average have approximately the minimum mean individual weight, wmin. It is therefore simply
| 2.1 |
The upper bound defines the maximum biomass that a population of N individuals can attain. This will be defined by energetic constraints and by the niche size. It is well established that metabolic rate per unit mass declines with body size for animals, suggesting that the same total energy flux would support a larger biomass of a large bodied species than a smaller bodied species. However, set against this trend is the fractal nature of niche space that results in an increasing availability of niche space with declining size and weight of the organism. These conflicting factors mean that the slope of the upper bound of the triangle could potentially range from negative to positive and may vary between communities and the organisms under study. For some communities, there may be a maximum biomass carrying capacity that can be supported which is approximately independent of numerical abundance and individual body size so that the upper bound can be assumed to be a constant.
If we know how species are distributed within this space, we can use the boundaries of the triangular domain to link the SADs in the alternative currencies (figure 1). We predict that this distribution will lie between regular and random for the following reasons. First, the amount of habitat space available increases with declining size of an organism. For any natural surface, the distance between two points is determined by the length of the ruler used for the measurement. A small ruler will track the bumps and hollows in a surface that a larger ruler ignores, with the result that the distance measured using the smallest ruler is the greatest. As the ruler length for an organism is its body size, the distances between points in the habitat will be greater for smaller individuals. For a single habitat and group of organisms, such as leaf beetles, the relationship between number of individuals (N) belonging to a single species and the average length of an individual, l, has been shown to be described by an equation of the form
| 2.2 |
where D is the fractal dimension of the habitat and k is a constant (Morse et al. 1985). D can take values between 2 and 3 for a surface such as the surface area of leaves or a coral reef. Morse et al. (1985) estimated that for arthropods on terrestrial vegetation, an order of magnitude decline in body length generated an increase of between 560-fold and 1780-fold in the number of individuals present, with the actual increase depending on the fractal dimension of the habitat. Gunnarsson (1992) found a similar relationship for spiders. Groups of species of differing size that share the same spatial habitat and form a sequence with a fractal dimension, D, can be termed a spatial guild.
Samples from a complex ecosystem may comprise a number of spatial guilds, each describing the change in abundance of species living in different structures within the habitat (Lawton 1990). For example, in a marine community, spatial guilds within a single community may include one relating to the area of rocky shore, a second linked to the distribution of crevice volume, a third associated with biogenic reef area, a fourth with kelp surface and so on. For each spatial guild, there will be a different relationship between biomass and abundance that will depend, in part, on the fractal dimension, D. For a community comprising a number of guilds of varying D, there would be a tendency for the species to be scattered along a number of sequences across the triangle as shown diagrammatically in figure 2. These sequences might have positive or negative slopes depending on how biomass scales with number and the magnitude of D. The effect of having a number of guilds of different fractal dimension is therefore expected to result in the species distributed approximately regularly along a number of bands that may overlay one another, or may differ in slope or intercept (figure 2). While each sequence would be expected to show a high correlation between log mass and log number, the combination of sequences is predicted to produce a triangular pattern with a reduced correlation.
Figure 2.
Diagrammatic representations of how two spatial guild sequences, each with a different fractal dimension, D, could span the triangular space and distribute the species. Each line is for a different spatial guild, for example, benthic fishes and open water fishes.
Second, a number of factors will act together to randomize this guild patterning. Species do not have a fixed abundance or biomass. Not only do they change over a single season with growth, recruitment and death, but, for longer-lived species, populations change their size distribution and biomass between years as birth and death processes change. As a result, the relationship between the numerical abundance and biomass of a species will vary through time. So, whereas, on average, species will be arranged on the graph in a series of guild sequences as described above, a snapshot survey will capture only a single point around this long-term mean. In addition, the distribution of species on the plot will be affected by stochastic sampling error. If the above considerations are correct, they will result in a different form to the SAD depending on the use of biomass or numerical abundance as currency (figure 1).
3. Predicted forms of the sad under different sampling regimes
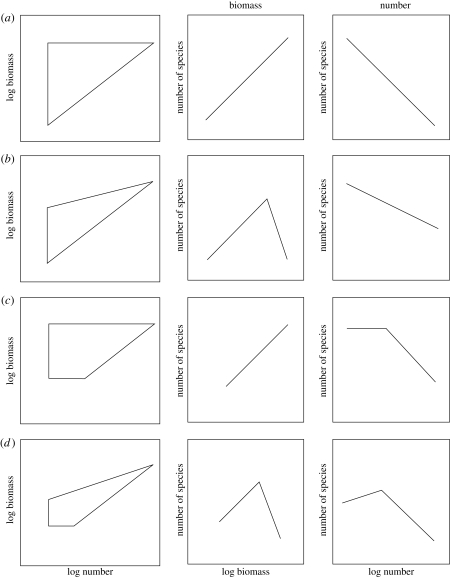
Our approach draws on the observation that communities are composed of species that vary in body size. Sampling considerations, such as the decision to focus on a particular taxonomic group, or the use of selective gear such as plankton nets or light traps, may limit the size range of species included in an SAD (Southwood & Henderson 2000; Magurran 2004). To take an extreme example, although elephant, buffalo, termites and ants play major ecological roles in the African savannah community, large mammals and insects are almost never included in the same SAD. On a less extreme level, SADs for plants rarely encompass both trees and herbs. Our approach means that it should be possible to make predictions about the consequences that different sampling methods will have for the observed shape of the SAD. Figure 3 shows the range of distributions that will arise from the different biomass–numerical abundance couplets that we assume can be generated under different sampling regimes. We argue, for simplicity, that on a log–log scale the points are bounded within a straight-sided region and that within this region the individual species are distributed at random or are evenly dispersed. The shape of the SAD is easy to visualize as simply the distance across the polygon perpendicular to the x-axis for the number SAD and the y-axis for the biomass SAD.
Figure 3.
The predicted shape of the SAD in terms of both biomass and number for different log number–log biomass domains. It is assumed that the individual species are scattered at random within the polygons.
Figure 3a is the predicted form when all species with the sampled size range, irrespective of size, are sampled with equal efficiency and all sizes of population have the same potential maximum total biomass. This would only be likely when the range of weights of individual species is insufficiently great to generate an appreciable effect relating to the change in metabolism with body weight. This would therefore be predicted to occur when sampling was markedly size restrictive. It is notable that in figure 3a, frequency of species per class decreases with increasing numerical abundance but increases when abundance is measured in terms of biomass.
Figure 3b shows the pattern when the least numerically abundant species do not have the total biomass of the numerically most abundant forms. Because of the power relationship between metabolism and body weight this is predicted to be the natural state in many communities, but can also be a sampling artefact when large, low abundance species are under-sampled. For example, in fisheries studies, nets and other techniques used to sample typical fishes in the 101–104 g weight range are unsuitable for large sharks and other fishes with weights in excess of 105 g and thus fail to catch very large species. This effect can be seen in figure 4b where the upper left-hand corner of the triangle holds no fishes; the sampling method used for this study almost never caught fishes weighing greater than or equal to 10 kg. The SAD peaks at an intermediate biomass per species. Although the diagram represents this peak as the intercept of two straight lines, in practice this would form a peaked smooth curve because of the non-regular distribution of the individual species points within the triangle. This curve might, in some circumstances, be indistinguishable from a lognormal.
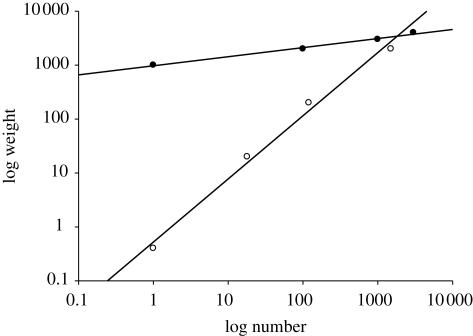
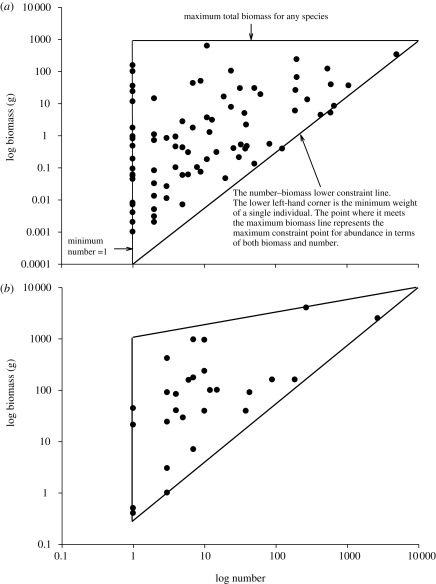
Figure 4.
The relationship between biomass and numerical abundance for two well-sampled communities. (a) The Milford Haven sub-tidal benthic community sampled by grab. (b) The Hinkley Bridgwater Bay fish community sampled using a nuclear power station cooling water intake in February 2008. Each dot represents the biomass and abundance for a single species. The maximum total biomass increases with number for the Hinkley dataset probably because fishes of large individual size (greater than 10 kg in weight) are under-sampled as they can avoid capture.
Figure 3c represents the situation where there is a lower cut-off in the mass of individuals sampled. This could occur, for example, when the mesh size of a net allows small individuals to escape capture or when stems below a certain diameter are excluded from a survey of trees. This cut-off results in a numerical abundance SAD with a possibly flat-topped maximum at the lowest abundance classes, similar to a lognormal distribution with a veil line close to the modal class, or to a log series distribution.
Figure 3d shows the region in which the random points would be scattered given a sampling cut-off in biomass for both the maximum and minimum size of individuals sampled. It is assumed that the unsampled large individuals can only occur in small numbers. Such sampling methodologies lead to SADs with a peaked distribution in both mass and number SADs which may approximate a lognormal in shape.
4. Empirical examination of biomass–abundance conversion
(a). Methods
We test our hypotheses that species lie within a triangular-shaped polygon, and that the distribution within this region lies between regular and random, using two thoroughly surveyed assemblages. In both cases sampling is intense, to ensure that most species present have been sampled, and completed within 1 day to exclude temporal change. We then use one of these communities (which has also been repeatedly sampled through time) to test our prediction that species belong to spatial guilds, and that these regular patterns are randomized by temporal shifts in the numerical abundance/biomass relationship.
(i). Marine benthic community
The Milford Haven marine benthic dataset comprises 52 Day grabs of 0.1 m2 each collected from sub-littoral soft sediment in Milford Haven, Pembrokeshire, Wales, in June 2007. The samples were collected from a grid of 12 stations with three or five replicate grabs at each station. The individual samples were passed through a 0.1 mm sieve and all the animals in the retained sample were picked under a lens. The individuals in each sample were identified to the species and the blotted wet weight of each species in each sample measured to the nearest 0.001 g. For this analysis, the sum of the number and biomass of each species over all 52 samples was used. Quality control assessments were undertaken with four randomly selected samples re-picked. No species not previously recorded from the first pick were detected in the four samples re-picked. The second pick generally comprised very small molluscs, which are easily missed because the substratum held large amounts of shell. The second pick held between 0.547 and 7.15 per cent the biomass of the first, indicating that the first pick consistently collected greater than 90 per cent of the total biomass and between 9.44 and 21.3 per cent of the number of individuals collected in the first sample, indicating that the first pick removed greater than 80 per cent of the individuals present. It was therefore concluded that the summed total over the 52 samples gave an accurate measurement of the relative abundance of the benthic macrofauna both in terms of biomass and number.
(ii). Estuarine fish and macro-crustacean community
For the Hinkley fish and macro-crustacean study, 6 h of sampling from two intakes of Hinkley B filter screens was undertaken in February 2008. Hinkley Point B Nuclear Power Station is situated on the southern bank of the Bristol Channel in Somerset, UK, and the intakes placed in front of a rocky promontory within Bridgwater Bay to the east are the extensive Stert mud flats with an intertidal area of about 40 km2. The water intakes are placed between −1 and −5 m mean low water spring so the fishes are sampled from water varying between 8 and 18 m in depth. A full description of the intake configuration and sampling methodology is given in Henderson & Seaby (1994). The standard lengths (SL) of all captured fishes were recorded to the nearest millimetre and weighed to the nearest 0.1 g. The filter screens have a solid square mesh of 10 mm and start to retain fishes greater than 25 mm SL. Complete retention for many species occurs at SLs > 40 mm. For fishes such as sprat, whiting and pout, the screens will retain all fishes captured with an SL greater than approximately 60 mm (Turnpenny 1981). The sampling method will therefore catch adults and juveniles older than six months for all known British marine fishes. The February sample comprised 679 individuals from 24 species of fishes and 2736 individuals from six species of crustacean.
(iii). Distribution of points within triangle
A nearest neighbour method is used to test the pattern of scatter of the species. The nearest neighbour index (NNI) is defined as
| 4.1 |
and can detect clumped, random or regular distributions (Belcher 2008), where A is the area of the region containing the species, n the number of species and L the average distance between species. The species are clustered when NNI = 0, regularly spread when the index is close to 2.15 and distributed at random when the index is around 1. For large n and a 5 per cent significance level, the null hypothesis of the points being randomly distributed is rejected in favour of them being clustered if NNI < 1 − 1.64(0.522/√n) and tending to regular if NNI > 1 + 0.86/√n (Belcher 2008). For small n, critical values are placed further from 1 and are given graphically at http://geographyfieldwork.com/nearest_neighbour_analysis.htm. For the values of n used here, the upper value of the NNI for randomness to be accepted is in the region of 1.2.
(iv). Spatial guild analysis
To test for the existence of spatial guilds, an intensive period of sampling was undertaken at Hinkley Point between late February and July 2009. Fourteen samples were each collected over 24 h from four intake screens in a similar fashion to that described above for the standard sampling regime. This sample was approximately 100 times the size of a typical monthly sample and comprised approximately 20 000 individuals from 49 fish species. We asked if three groups of fishes that use the habitat in contrasting ways formed identifiable spatial guilds across the log numerical abundance–log biomass plot. The first group comprised benthic fishes such as plaice, Pleuronectes platessa, and sole, Solea solea; these are typically found on the sea bed. The second group consisted of pelagic fishes such as the herring family that live in open water and avoid surfaces. Our third group, termed proximo-benthic, swim in proximity to surfaces and structures but usually avoid touching the substrate; typical examples are members of the cod family. To demonstrate that the fishes from the three spatial guilds had different relationships between numerical and biomass abundance, power curves were fitted to each sequence using linear regression on the logged abundance data.
(v). Randomizing factors: temporal shifts in numerical abundance/biomass position of species
To examine the temporal variation in the biomass and numerical abundance of individual species, 24 consecutive monthly samples collected from January 1987 were used. While regular monthly abundance data have been collected from 1981 to the present, this was the only extended period when the number and weight of all individuals in every sample were recorded. Each sample was collected in similar manner to the February 2008 sample described above.
(b). Results
(i). The triangular nature of the log numerical abundance–log biomass plot
As expected, the species in both communities lie within a triangular region. The Milford Haven marine benthic community (figure 4a) forms an approximately right-angled triangle. The NNI for these data is 1.185. The critical upper value for randomness for n = 84 species at the 5 per cent level is 1.202, indicating that the observed distribution did not differ significantly from a random one. In the second example, the estuarine fishes and crustacean species lie within an obtuse triangle, with an NNI of 1.260, for n = 28 species (figure 4b). As the critical value at the 5 per cent level for a random distribution is 1.220, we conclude that this dataset shows a weak tendency towards regularity.
The clear difference in shape between these two triangles may, in part, be owing to the under sampling of large, low abundance, fishes species in the Bridgwater Bay dataset. The sampling method is unlikely to capture fishes greater than 10 kg in weight and greater than 1 m in length, such as sharks, because they have the swimming ability to escape the intake. By contrast, the grab sampler used in Milford Haven was able to sample the full size range of benthic invertebrates present.
(ii). Evidence for spatial guilds
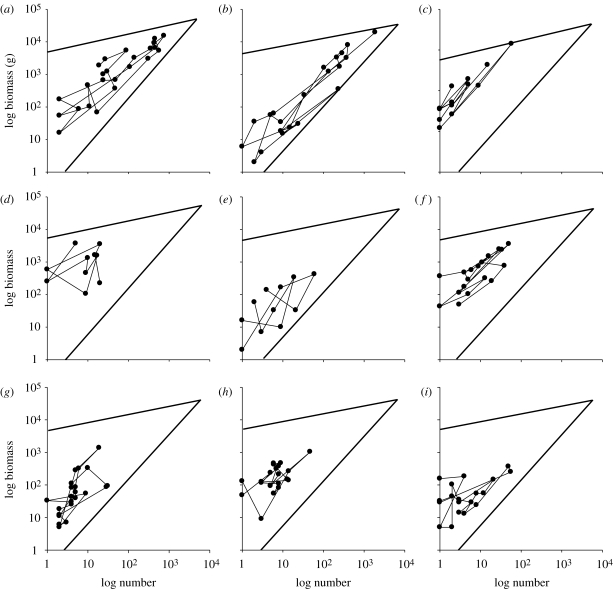
Figure 5 shows the dispersion and different slopes for three spatial guilds, together with the total plot for all species of fishes collected from Bridgwater Bay between February and July 2009. All three sequences have different fitted power curves. The flatfishes comprise a discrete group of five bottom-living species morphologically adapted to rest camouflaged on the seabed. For this flatfish guild, the fitted curve was M = 0.0631N0.904, R2 = 0.95. The pelagic guild comprises clupeiform fishes that actively swim in open water and avoid all surfaces; for this group M = 0.0627N0.6328, R2 = 0.88. This guild differs in slope from the flatfishes but has a similar intercept. The third group comprises species belonging to the cod family. These proximo-benthic fishes live close to underwater structures but do not rest on the seabed nor do they enter or live in holes in the seabed. These had a fitted curve described by the equation M = 0.0123N1.0423, R2 = 0.95. The coefficient of determination, R2, for the entire dataset is 0.63, appreciably lower than for individual niche sequences as predicted. A test of coincidence between the three regression coefficients did not show a significant difference between the three regression lines at the 5 per cent level (F4,10 = 2.42, p = 0.11).
Figure 5.
(a) The log number–log biomass triangle generated by an intensive period of study of the fish in Bridgwater Bay collected between February and July 2009. The log number-log biomass relationships for three spatial guilds comprising (b) the benthic flatfishes, (c) pelagic open water fishes and (d) the proximo-benthic cod family are each plotted together with their power curves fitted by linear regression.
All three groups of fishes showed a positive, statistically significant, correlation between the numerical abundance and biomass but no single group alone generated the triangular pattern typically observed for entire communities. The triangular form of the log number–log biomass relationship begins to form when the three sequences are combined.
(iii). Evidence for randomizing factors
Figure 6 shows the position of the nine commonest fish species in 24 monthly samples collected from Bridgwater Bay between 1987 and 1989, a period when number and weight were systematically recorded. The points are joined in temporal order. Movements within the triangle are particularly extensive for the two commonest species, sprat and whiting. These plots demonstrate that even over small periods of time species do not maintain fixed places within the numerical abundance–biomass triangle. However, it is clear that species do not move at random throughout the area but tend to be distributed around individual, different, centres of gravity. A discriminant function analysis showed the differences in the centroids of the nine fish species to be highly significantly different (Wilk's lambda = 0.6573, F = 4.348, d.f. = 16, p = 1.1 × 10−7).
Figure 6.
The changing relationship between biomass and numerical abundance for the common fishes caught in Bridgwater Bay over 24 consecutive monthly samples. The plots are for the most abundant species in terms of biomass or numerical abundance. (a) Whiting, (b) sprat, (c) five bearded rockling, (d) cod, (e) dab, (f) flounder, (g) sole, (h) pout, and (i) poor cod.
4. Discussion
We have drawn on ecological insights to relate the SADs that arise when species abundances are measured in the alternative currencies of numerical abundance (number of individuals) and biomass. Theory, together with simple assumptions, indicates that when species are plotted on a log–log plot using both measures of abundance, they will lie within a roughly triangular area. Two intensively sampled communities support this conjecture. If we are to link the SADs for the different currencies, we need to know not just the shape of this triangular domain, but also the distribution of species within it. We argued that three factors will lead the species to adopt an approximately random distribution. These are: (i) the fractal nature of niche space and the presence of spatial niche guild sequences, (ii) the natural variation in the biomass–abundance of individual species through time, and (iii) stochastic variation in abundance and sampling. Factor (i) would nudge the species towards a regular pattern, while factors (ii) and (iii) will randomize this distribution. Our data support our prediction that the species distribution within the abundance/biomass triangle lies between random and regular, but we await data from additional communities to confirm that this is generally true.
Our results suggest that large communities may be divided into different spatial guilds each comprising species that use space or other resources in a different fashion. We believe this is the primary explanation for the triangular shape of the log biomass–log numerical abundance plot. If this is the case, then these sequences will be acting to distribute the species across the plot. We therefore predict that a triangular plot will not occur if a study is limited to a selected group of organisms forming a sequence within a single spatial component of the habitat, for example, insects on tree bark or fishes in leaf-litter banks.
There is an ongoing debate about the extent to which resource apportionment can be inferred from the distribution of numerical abundance. Some models, for instance, the Sugihara (1980) sequential breakage model and the Hubbell (2001) neutral model, are framed in terms of numbers of individuals and assume that these distributions are indicative of the way that species divide resources. This assumption is supported by a number of empirical and modelling studies (e.g. Sugihara 1989; Taper & Marquet 1996; Marquet et al. 2003). A second set of investigations, also drawing on data and allometric theory, indicate that numerical abundance and biomass can provide different insights into assemblage structure (e.g. Harvey & Godfray 1987; Pagel et al. 1991; White et al. 2004; Connolly et al. 2005).
Our results support Morlon et al.'s (2009) contention that there is no single answer to the question. They show that while there are cases, for example, when the species are all sampled from a single guild sequence, in which numerical abundance is a proxy of biomass (and hence resource use), this is not automatically the case. Our view that the relationship between the distributions of numerical abundance and biomass is mediated by body size is supported by research on desert rodents. Using a long-term dataset, White et al. (2004) conclude that changes in species composition and the distributions of numerical abundance and biomass can result from changes in masses of the individual species—even if overall energetic availability remains constant. They suggest that shifts in body size are linked to changes in the desert system itself, such as the transition from grassland to shrubland. The idea that there is an ecological space, bounded by the upper and lower limits of biomass and numerical abundance and constrained by body size, has implications for species packing. Although the numerical abundance of desert rodents increased over time (White et al. 2004), this was matched by a decrease in biomass, community energy use remained approximately constant and species richness did not vary. In the same way, increased species richness at lower latitudes could be linked to the increase in the numerical abundance–biomass envelope in tropical systems relative to temperate ones.
Guild sequences assume that species differ in their use of space and resources and the amount of resource available to them. It is becoming clear that SADs should not treat species as identical (MacNally 2007; Alonso et al. 2008). If species differences are insignificant, then one would expect the various measures of abundance to be proportional to one another, thereby resulting in similar SADs across currencies. This study and others suggest that this is not the case. It is also evident that partitioning a SAD can shed light on the processes that underpin community structure (McGill et al. 2007). Previously, we showed how a temporal partition of species presence into core members of the community that are almost always present and occasional migrants can help explain the form of an SAD (Magurran & Henderson 2003). Here, we have found that partitions based on spatial niche use can also be illuminating. Heterogeneity in species resource use in time and/or space may underpin multimodality in empirical SADs (Dornelas & Connolly 2008; Dornelas et al. 2009).
Our analysis offers an explanation for the wide range of forms for SADs reported from empirical studies. As shown in table 1, the form of SADs depends on a combination of both the unit of measurement for abundance and the variation in sampling efficiency with organism size. There are strong arguments in favour of the combined use of both biomass and numerical abundance as this will more clearly show the influence of sampling strategy on the form of the SAD.
Table 1.
A summary of the predicted form of SADs when measured as biomass and numerical abundance for different sampling regimes.
| sampling regime | log biomass–log number relationship | SAD using biomass | SAD using numerical abundance |
|---|---|---|---|
| sampling restricted to a single group of organisms which all belong to the same spatial guild | biomass and numerical abundance correlated; no triangular distribution apparent | the SAD relationship cannot be inferred | the SAD relationship cannot be inferred |
| all organisms over a wide size range sampled with similar efficiency | biomass–abundance plot distribution forms an approximately right-angled triangle if maximum biomass is independent of numerical abundance (figure 3a) | number of species–log biomass plot reaches a maximum at the highest biomass category | number of species–log abundance plot reaches a maximum at the lowest abundance category |
| large organisms under-sampled | biomass–abundance plot distribution forms an obtuse triangle (figures 1 and 3b) | SAD peaks at an intermediate biomass category; it may approximate a lognormal distribution | number of species–log abundance plot reaches a maximum at the lowest abundance category |
| small organisms under-sampled | biomass–abundance plot distribution forms polygon ideally like an approximately right-angled triangle with the lower corner cut-off (figure 3c) | number of species–log biomass plot reaches a maximum at the highest biomass category | SAD with a maximum at the lower abundance classes; may be similar to a lognormal with veil line |
| both large and small organisms under-sampled | biomass–abundance plot distribution forms polygon ideally approximately kite-shaped (figure 3d) | SAD peaks at an intermediate biomass category; it may approximate a lognormal distribution | SAD peaks at an intermediate abundance category; it may approximate a lognormal distribution |
Finally, our approach will allow researchers to predict changes in the SADs of biomass and numerical abundance in impacted communities relative to their undisturbed counterpart (MacNally 2007). The different responses of numerical abundance and biomass to pollution have already been noted (Warwick 1986). Our method shows how changes in the SADs come about and provides a framework in which the responses of individual species to disturbance can be understood.
Acknowledgements
We thank Dr Richard Seaby and Mr Robin Somes for assistance with fieldwork and Ms Rowena Henderson and Dr Claire Henderson for sample sorting and weighing. A.E.M. is a member of the NCEAS working group on ‘Tools and fresh approaches for species abundance distributions’ and thanks her colleagues there for many stimulating discussions on SADs. She also acknowledges the Royal Society of Edinburgh for a support fellowship. Since studies began at Hinkley Point in 1981 many organizations have financially supported the fieldwork, including the Central Electricity Generating Board, National Power Plc, Nuclear Electric Plc and the Environment Agency. The two anonymous referees made important contributions to the final form of this paper.
References
- Alonso D., Ostling A., Etienne R. S.2008The implicit assumption of symmetry and the species abundance distribution. Ecol. Lett. 11, 93–105 (doi:10.1111/j.1461-0248.2007.01127.x) [DOI] [PubMed] [Google Scholar]
- Belcher P.2008Nearest neighbour: a test to see if data points attract one another, repel one another or are randomly distributed. Int. J. Math. Educ. Sci. Technol. 39, 371–383 (doi:10.1080/00207390701607315) [Google Scholar]
- Brown J. H., Gillooly J. F., Allen A. P., Savage V. M., West G. B.2004Toward a metabolic theory of ecology. Ecology 85, 1771–1789 (doi:10.1890/03-9000) [Google Scholar]
- Connolly S. R., Hughes T. P., Bellwood D. R., Karlson R. H.2005Community structure of corals and reef fishes at multiple scales. Science 309, 1363–1364 (doi:10.1126/science.1113281) [DOI] [PubMed] [Google Scholar]
- Dornelas M., Connolly S. R.2008Multiple modes in a coral species abundance distribution. Ecol. Lett. 11, 1008–1016 (doi:10.1111/j.1461-0248.2008.01208.x) [DOI] [PubMed] [Google Scholar]
- Dornelas M., Moonen C., Magurran A. E., Barberi P.2009Species abundance distributions reveal environmental heterogeneity in modified landscapes. J. Appl. Ecol. 46, 666–672 (doi:10.1111/j.1365-2664.2009.01640.x) [Google Scholar]
- Gunnarsson B.1992Fractal dimension of plants and body size distribution in spiders. Funct. Ecol. 6, 636–641 (doi:10.2307/2389957) [Google Scholar]
- Harvey P. H., Godfray H. C. J.1987How species divide resources. Am. Nat. 129, 318–320 (doi:10.1086/284638) [Google Scholar]
- Henderson P. A., Seaby R. M. H.1994On the factors influencing juvenile flatfish abundance in the lower Severn Estuary. Neth. J. Sea Res. 32, 321–330 (doi:10.1016/0077-7579(94)90009-4) [Google Scholar]
- Hubbell S. P.2001The unified neutral theory of biodiversity and biogeography. Princeton, NJ: Princeton University Press [Google Scholar]
- Kleiber M.1962The fire of life. New York, NY: Wiley [Google Scholar]
- Lawton J. H.1990Species richness and population dynamics of animal assemblages. Patterns in body size: abundance space. Phil. Trans. R. Soc. Lond. B 330, 283–291 (doi:10.1098/rstb.1990.0199) [Google Scholar]
- MacNally R.2007Use of the abundance spectrum and relative-abundance distributions to analyze assemblage change in massively altered landscapes. Am. Nat. 170, 319–330 (doi:10.1086/519859) [DOI] [PubMed] [Google Scholar]
- Magurran A. E.2004Measuring biological diversity. Oxford, UK: Blackwell Science [Google Scholar]
- Magurran A. E., Henderson P. A.2003Explaining the excess of rare species in natural species abundance distributions. Nature 422, 714–716 (doi:10.1038/nature01547) [DOI] [PubMed] [Google Scholar]
- Marquet P. A., Keymer J. E., Cofré H.2003Breaking the stick in space: of niche models, metacommunities and patterns in the relative abundance of species. In Macroecology: reconciling divergent perspectives on large scale ecological patterns (eds Gaston K. J., Blackburn T. M.), pp. 64–84 Oxford, UK: Blackwell [Google Scholar]
- McGill B.2003Does Mother Nature really prefer rare species or are log-left-skewed SADs a sampling artefact? Ecol. Lett. 6, 766–773 (doi:10.1046/j.1461-0248.2003.00491.x) [Google Scholar]
- McGill B. J., et al. 2007Species abundance distributions: moving beyond single prediction theories to integration within an ecological framework. Ecol. Lett. 10, 995–1015 (doi:10.1111/j.1461-0248.2007.01094.x) [DOI] [PubMed] [Google Scholar]
- Morlon H., et al. 2009Taking species abundance distributions beyond individuals. Ecol. Lett. 12, 488–501 (doi:10.1111/j.1461-0248.2009.01318.x) [DOI] [PubMed] [Google Scholar]
- Morse D. R., Lawton J. H., Dodson M. M., Williamson M. H.1985Fractal dimension of vegetation and the distribution of arthropod body lengths. Nature 314, 731–733 (doi:10.1038/314731a0) [Google Scholar]
- Motomura I.1932On the statistical treatment of communities. Zool. Mag. Tokyo (in Japanese) 44, 379–383 [Google Scholar]
- Pagel M. D., Harvey P. H., Godfray H. C. J.1991Species-abundance, biomass and resource-use distributions. Am. Nat. 138, 836–850 (doi:10.1086/285255) [Google Scholar]
- Preston F. W.1948The commonness, and rarity, of species. Ecology 29, 254–283 (doi:10.2307/1930989) [Google Scholar]
- Saint-Germain M., Buddle C. M., Larrivée M., Mercado A., Motchula T., Reichert E., Sackett T. E., Sylvain Z., Webb A.2007Should biomass be considered more frequently as a currency in terrestrial arthropod community analysis? J. Appl. Ecol. 44, 330–339 (doi:10.1111/j.1365-2664.2006.01269.x) [Google Scholar]
- Southwood R., Henderson P. A.2000Ecological methods. Oxford, UK: Blackwell Science [Google Scholar]
- Sugihara G.1980Minimal community structure: an explanation of species abundance patterns. Am. Nat. 116, 770–787 (doi:10.1086/283669) [DOI] [PubMed] [Google Scholar]
- Sugihara G.1989How do species divide resources? Am. Nat. 133, 770–787 (doi:10.1086/284929) [Google Scholar]
- Taper M. L., Marquet P. A.1996How do species really divide resources? Am. Nat. 147, 1072–1068 (doi:10.1086/285893) [Google Scholar]
- Thibault K., White E., Ernest S. K. M.2004Temporal dynamics in the structure and composition of a desert rodent community. Ecology 85, 2649–2655 (doi:10.1890/04-0321) [Google Scholar]
- Turnpenny A. W. H.1981The use of multiple regression analysis in formulating operating strategies for power impingement problems. Report of the Central Electricity Generating Board, UK, RD/L/2043N81 [Google Scholar]
- Warwick R. M.1986A new method for detecting pollution effects on marine macrobenthic communities. Mar. Biol. 92, 557–562 (doi:10.1007/BF00392515) [Google Scholar]
- White E. P., Ernest S. K. M., Thibault K.2004Trade-offs in community properties through time in a desert rodent community. Am. Nat. 164, 670–676 (doi:10.1086/424766) [DOI] [PubMed] [Google Scholar]
- Wilson W. G., Lundberg P.2004Biodiversity and the Lotka–Volterra theory of species interactions: open systems and the distribution of logarithmic densities. Proc. R. Soc. Lond. B 271, 1977–1984 (doi:10.1098/rspb.2004.2809) [DOI] [PMC free article] [PubMed] [Google Scholar]