ROBUST MAXIMUM LIKELIHOOD ESTIMATION IN Q-SPACE MRI

Abstract

Q-space imaging is an emerging diffusion weighted MR imaging technique to estimate molecular diffusion probability density functions (PDF's) without the need to assume a Gaussian distribution. We present a robust M-estimator, Q-space Estimation by Maximizing Rician Likelihood (QEMRL), for diffusion PDF's based on maximum likelihood. PDF's are modeled by constrained Gaussian mixtures. In QEMRL, robust likelihood measures mitigate the impacts of imaging artifacts. In simulation and in vivo human spinal cord, the method improves reliability of estimated PDF's and increases tissue contrast. QEMRL enables more detailed exploration of the PDF properties than prior approaches and may allow acquisitions at higher spatial resolution.

1. INTRODUCTION

Q-space imaging is an analysis technique for diffusion weighted (DW) magnetic resonance (MR) imaging that shows great promise as a tool to study tissue microstructure [1]. As with other DW imaging techniques, the Brownian motion of water within a voxel is noninvasively inferred from signal attenuations observed in the presence of sensitization gradients. Rather than assuming a Gaussian distribution for the water diffusion probability density function (PDF) as in diffusion tensor imaging (DTI), q-space analyses experimentally determine non-parametric PDF's for single diffusion directions. The PDF represents the probability that a spin (i.e., water hydrogen) diffuses a particular distance from its initial position during the DW time. To date, q-space studies reported in the literature have used limited diffusion models to regularize noisy data. These models make ad hoc assumptions and do not accurately account for the properties of MR noise. This study presents a robust M-estimator for estimating PDF's from q-space data that accounts for Rician distributed noise. This novel approach specifically addresses the joint likelihood of all observations within a general non-parametric model, denoted Q-space Estimation by Maximizing Rician Likelihood (QEMRL).

Noise in magnitude MR data is well to know to be Rician distributed and to introduce intensity bias at low SNR [2]. The observed signal intensity (S) distribution is

$$<no>\left(1\right)<∕no>p(S;S_0,\sigma )=\frac{S}{{\sigma }^2}{e}^{-\frac{s^2+s_0^2}{2{\sigma }^2}}{I}_0\left(\frac{{\mathit{SS}}_0}{{\sigma }^2}\right),$$

where S₀ is the noise free signal and σ is the standard deviation of the noise on the unobserved complex valued images. Maximum likelihood (ML) approaches for bias correction have been presented for scalar MR images [3]. Recently, ML methods have been extended to estimate tensors in DTI [4], but ML has not yet been applied to q-space imaging.

Rician noise distorts calculated PDF's from GM (gray matter) and WM (white matter) differently and, thus, reduces tissue contrast. In q-space imaging, q is an experimental parameter that modulates signal attenuation related to diffusion. In GM, the acquired signal at large q is highly attenuated (indicating that diffusion is relatively unrestricted), so the observed signal is substantially biased by Rician noise. The bias in Fourier space leads to artifactual sharpening of the calculated PDF (i.e., high pass filtering). Meanwhile, in WM, the acquired signal at large q is less attenuated due to tight restriction boundaries, so there is less bias and the PDF is less distorted. Since the Rician noise introduces more PDF sharpening in GM than WM, the calculated PDF's for these tissue types are more similar than they would be if calculated from noise free data.

Prior approaches to q-space imaging have recognized that using substantially biased observations has a detrimental impact on the calculated results, but have not considered the noise in a likelihood framework. Two compartment models have been fit to limited datasets to reduce the impact of noise and avoid complexities in calculated PDF's [5]. For more general q-space imaging, Assaf et al. replaced all observations below twice a noise level estimate with zero and extrapolated any non-zero signals with a bi-Gaussian [1]. Farrell et al. calculated a “noise floor” and subtracted this level from the observed signal and also extrapolated non-zero signals with a bi-Gaussian [6]. These level adjustment approaches can be viewed as adaptive low-pass filters. The extrapolation step uses prior parametric assumptions to increase apparent resolution and reduce ringing. These methods partially address the problem of sharpened PDF's, but they are heuristics and do not make optimal use of all available data.

The key principle of the new method is an explicit accounting for the noise properties in the DW images that constitute a q-space dataset. In simulation, we show that QEMRL estimates PDF derived contrasts (e.g., mode probability, P0, full width at half maximum, FWHM, and the root mean square displacement, RMSD) that are closer to their true (i.e. noise-free) values. When applied to in vivo human spinal cord dataset, QEMRL improves the reliability of PDF estimation and increases tissue contrast. Finally, we present a compact and intuitive visual representation of the information obtained with the PDF, and discuss how robust estimation of the PDF may aid the assessment of diffusion properties in multiple sclerosis (MS) lesions.

2. METHODS

In q-space imaging, the Fourier transform of the diffusion PDF is sampled through DW acquisitions with different diffusion sensitizations (Fig. 1). The observed signal is

$$<no>\left(2\right)<∕no>S\left(q\right)=S\left(0\right)\int p_t\left(r\right)\exp \left(i2\pi \mathit{qr}\right)\mathit{dr}~{\mathcal{F}}^{-1}\left\{p_t\left(r\right)\right\},$$

where S(q) is the observed signal at q (an experimental parameter) and p_t(r) is the PDF that a spin moves a distance of r in time t. Typically, the sampling locations are regularly spaced in q (with fixed t), and a discrete Fourier transform is used to recover p_t(r) under the assumption that the PDF is sufficiently band limited.

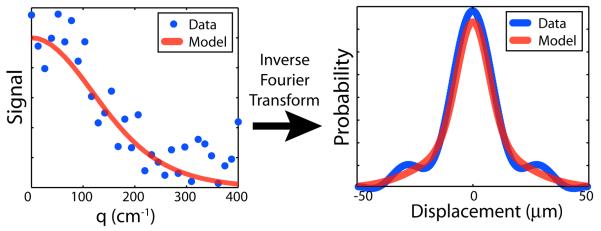
Fig. 1.

In a general q-space experiment, data are observed at regularly spaced q-values (left), which are transformed to PDF's (right). To improve reliability over direct calculations (note ringing on data curve at right), data are typically fit with a model. In QEMRL, the fitting process utilizes a maximum likelihood model.

The attenuation signal was modeled as a positive mixture of Gaussian distributions restricted to a physically realistic range of diffusivities (3 × 10⁻⁵ to 3 × 10⁻³ mm²/s). The number of Gaussian components was determined for each voxel with sequential search using an L-curve criterion on log-likelihood. To maintain a non-parametric approach, the number of mixtures was intentionally selected higher than would be indicated by a Bayesian information theoretic criteria. Huberization (truncation) of the likelihood measure reduced the impact of artifacts; the truncation point was adaptively determined from the data. To regularize the estimate, a Gaussian Bayesian prior was placed on the noise level with a mean of the initial estimate (σ̂₀) and ten percent standard deviation. The optimal solution was numerically found by a coordinate descent Nelder-Mead simplex algorithm[4]. For a mixture of j components, the objective function was

$$<no>\left(3\right)<∕no>\left\{\widehat{{\mathcal{N}}_{1\dots j}}\right\}={\mathrm{argmax}\mathcal{L}}^{\ast }\left(S\left(q_{1\dots N}\right)\right);{\mathcal{N}}_{1\dots j},\sigma ),$$

where S(q_i) are the observations at N q-values and 𝒩_j is a zero mean Gaussian with restricted variance. The robust likelihood (𝓛*) incorporated Huberization (ℋ) and a Bayesian prior with the traditional likelihood (𝓛) of each observation under a Rician noise model (Eq.1),

$$<no>\left(4\right)<∕no>{\mathcal{L}}^{\ast }\left(S(q_{1\dots N};•)\right)=p(\sigma ;{\widehat{\sigma }}_0)\prod _{i=1}^N\mathcal{H}\left(\mathcal{L}(S\left(q_i\right);•)\right).$$

The search was initialized with a minimum mean squared error solution and a spatially varying noise level estimate using the method presented in [4] where a robust Q_n scale metric was used in place of the sample standard deviation [7].

The mixture model provides analytic representations of the attenuation signals, so PDF's may be recovered without use of the discrete Fourier transform. Note that the inverse Fourier transform of a positive mixture of zero-mean Gaussians is also a positive mixture of zero-mean Gaussians. Thus, the estimated PDF's are guaranteed to be monotonically decreasing, strictly positive, and symmetric, which is in accordance with physical principles. Since the Fourier transform is linear, estimated ML attenuation signals represent ML PDF's.

3. SIMULATIONS

Simulations were performed with two-component exponential mixtures (with diffusivities drawn at random from 3 × 10⁻⁵ to 3 × 10⁻³ mm²/s) (Fig. 2). Each simulation consisted of two repetitions of 32 data points that linearly spanned the signal decay curve from q=0 to 400 cm⁻¹ at an SNR of 7:1 on the q=0 images. The SNR on other DW images is variable and depends on signal attenuation. For comparison, a traditional two compartment bi-Gaussian (Bi-Gaus) method was implemented that discarded all data with intensity less than the noise level.

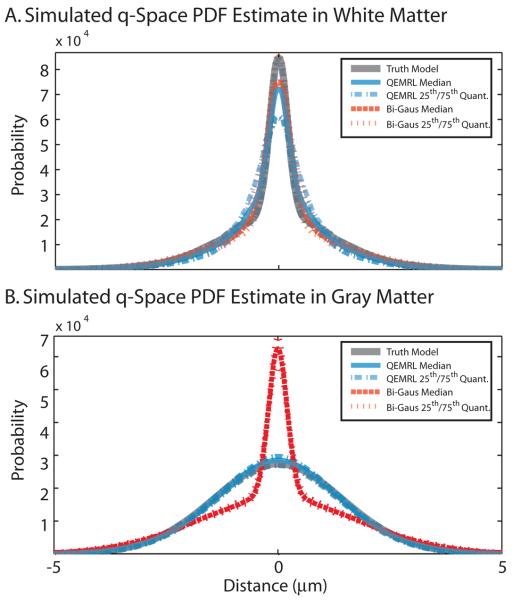
Fig. 2.

Two compartment (bi-Gaussian) simulations demonstrate that QEMRL slightly improves performance for white matter (A) and greatly improves performance for gray matter (B). QEMRL estimates show much less bias towards artifactual sharpening of broad PDF's than a traditional approach.

QEMRL reduced the median MSE on the estimated PDF by 95% (25th-75th quantiles: 78-99%) compared to the Bi-Gaus method. For simulations that used low diffusivities (representative of WM, Fig. 2A), QEMRL offered less of an improvement over Bi-Exp (21%), which is to be expected as the bi-exponential model contains a parsimonious representation of the truth model when little Rician bias is present. However, for simulations that used high diffusivities (representative of GM, Fig. 2B), QEMRL was able to more accurately account for the bias due to the “noise floor” and offered substantial improvements (98%).

4. IN VIVO EXPERIMENTS

The QEMRL technique was studied in the in vivo human spinal cord. Four repetitions of a standard q-space protocol were acquired for a healthy volunteer on a 3T Philips MR scanner. Thirty axial slices were acquired perpendicular to the long axis of the spinal cord covering C2 to C6 (1.3×1.3×3.0 mm, FOV=84×84×90 mm, matrix=64×64, 32 linearly spaced q-values from 0 to 414 cm⁻¹) with single-shot EPI (SENSE=1.8, TR/TE=7000/106 ms). To improve SNR and mitigate the impacts of artifacts, each DW image was collected with diffusion weighting along two orthogonal directions ([Gx, Gy, Gz]=[1,1,0] and [1,−1,0]) with a total acquisition time of ~10 min. The SNR was ~7:1 on the q=0 images. A second control and one patient with MS were each scanned once with a similar q-space protocol (TE=112 ms, FOV=62×62×90 mm, matrix=48×48). Structural images were acquired for lesion identification (spin density/T2*w 3D-GRE with three-shot EPI, SENSE=2). Informed written consent and local institution review board approval were obtained prior to study.

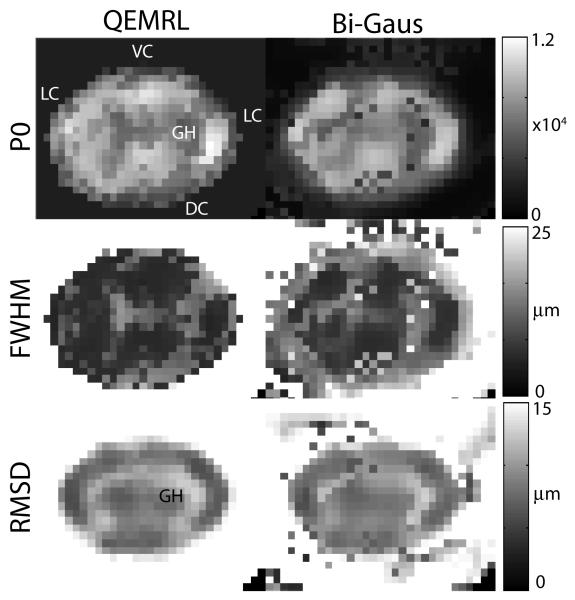
In the scan-rescan dataset, QEMRL reduced the mean variability of estimated PDF's within the spinal cord by 30% over the Bi-Gaus method. The adaptive model order selection procedure identified 3.6 ± 1.1 mixture compartments per voxel within the spinal cord. QEMRL more clearly revealed GM/WM contrast in the cervical spinal cord in the P0, FWHM, and RMSD contrasts (Fig. 3).

Fig. 3.

QEMRL increases contrast between the gray matter horns (GH) and the spinal cord white matter, include the lateral (LC), dorsal (DC), and ventral (VC) columns.

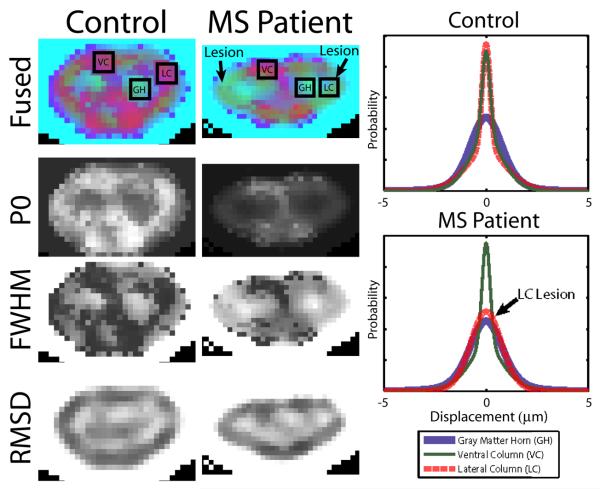
Results for a representative slice for the healthy control (Fig. 4) show that PDF's in WM are tall and narrow, whereas PDF's in GM are low and broad. Results are also shown for the MS patient with lesions in the lateral columns (hyperintense on the T2*w GRE, not shown). MS lesions show abnormal height and shape of PDF's; however, quantitative analysis of the PDF's is complicated by the high dimensionality. To address this complexity, the PDF shape is often summarized by the P0 and FWHM properties, however, this fails to describe the extent to which the observed PDF is truly non-Gaussian. Analysis of the RMSD captures information relating to the heavy tails.

Fig. 4.

Slices at the level of C4 are shown for a control (left) and a MS patient with a LC lesion (center). Mean PDF's within the indicated regions are presented at right.

These contrasts may be fused into a color image that imparts greater information about the PDF than any single contrast (Fig. 4 top row: red corresponds to P0, green to FWHM, and blue to RMSD). With this visualization technique, the differences between narrow and wide PDF's and the presence of heavy tails can be readily appreciated. P0 is most sensitive to strongly peaked PDF's which are indicative of highly restricted diffusion environments, such as in WM. FWHM tends to measure the width of the primary lobe, so a high FWHM indicates a weakly restricted diffusion environment. RMSD is also sensitive to weakly restricted environments, but places more emphasis on the tails of the distribution. In the multi-spectral images for the control, WM columns are primarily red/magenta, indicating peaked PDF's with narrow FWHM and RMSD. The central areas of the GM horns are green/teal, indicating a high FWHM, but a low RMSD. The dorso-lateral GM horns demonstrate a purple or light blue color, which indicate both a high FWHM and high RMSD. The purple hue appears to point out the transition between the dorsal and lateral columns in the control. These features may also be used to observe the regional extent of the MS lesions. The large lateral column lesions reduce P0 and increase FWHM (a decrease in the purple color) near the lesion boundaries.

5. DISCUSSION

Through improved estimation, QEMRL permits the wealth of information in diffusion PDF's to be more fully explored and utilized to assess microstructure in both healthy and diseased tissue. QEMRL improves the accuracy and reliability of PDF's derived from q-space by accounting for the Rician noise properties in magnitude images. Specifically, while the Rician bias at low SNR causes the PDF's computed with the Bi-Exp method to be artificially narrow (Fig. 2), QEMRL produces PDF's that more closely resemble the true PDF. Outlier rejection and stable numerical optimization reduce the impact of imaging artifacts and result in increased empirical q-space PDF reliability. Incidentally, QEMRL estimates a projection of PDF's onto a finite basis set, which has a physical interpretation as the mixture of diffusion compartments and may be useful as a biomarker for micro-structural changes. For example, the GM heterogeneity in the RMSD images seen in the posterior dorsal horns compared to the dorso-lateral anterior horn would not be apparent if the RMSD were derived from the FWHM (Fig. 3). With QEMRL, future studies may employ measures of Gaussianity beyond RMSD, such as kurtosis. These contrasts may be indicative of cytoarchitecture and structure within the GM, for example, due to differing WM concentrations related to merging of the dorsal root collaterals. Additionally, analysis of q-space data with QEMRL improves reliability of estimation process, which may allow acquisition at higher spatial resolution images that provide contrasts at an equivalent SNR to current techniques.

PDF's for water diffusion can be measured in vivo in the spinal cord, and are sensitive to tissue damage caused by MS. These PDF's contain a wealth of information (beyond the typically reported P0 and FWHM) and reveal interesting and subtle properties of the biophysical diffusion restriction environment. There is visual and quantitative heterogeneity in the spinal cord, which may be indicative of substructure within WM and GM. Further histological and theoretical validation will be necessary to determine if it is possible to attribute specific observations of PDF's to intra-voxel compartments (i.e., substructural differences) or to partial volume effects (i.e., mixtures of WM and GM within voxels).