Development of Contrast Mechanisms in Humans: A VEP Study

Abstract

Purpose

The visual system undergoes major developmental changes in infancy and continues to mature throughout childhood. This study was designed to investigate the developmental change in the contrast response function and the neural mechanisms that contribute to this change.

Methods

Participants were 29 infants from 15–28 weeks of age, 2 children, 1 adolescent, and 9 adults. Visual evoked potentials (VEPs) were elicited by horizontal square-wave gratings contrast-reversed at 7.5 Hz. Spatial frequencies of 0.75 and 1.5 c/deg were used, and contrast was swept in seven octave steps from 1 to 64% with an initial step at 0%. There were ten runs of each condition (8.5 s each). Fourier analysis was used to derive amplitude and phase of the dominant (second harmonic) frequency component in the response, which were then plotted vs. contrast. The empirical contrast response functions were fitted using a nonlinear model, which generates estimates of shunting inhibition, conductance, and the integrative time constant in the system.

Results

Typically, in comparison to older observers, contrast response functions in infants are relatively linear with increases in contrast, and they exhibit little if any contrast gain control (amplitude compression and phase advance with increasing contrast). Time constants in infants are longer than in adults, and infants demonstrate less decrease in time constant values with increasing contrast than do adults.

Conclusions

These results are consistent with greater shunting inhibition in the visual cortex of older observers.

Luminance contrast perception is an essential task of the visual system, and there are parallel neural pathways dedicated to the processing of positive and negative contrast information.¹ The behavior of the visual system associated with a contrast-modulated input signal is characterized by the contrast response function which is typically expressed in plots of amplitude and phase of the response vs. contrast. The slope of the amplitude plot is referred to as contrast gain (i.e., the amount of increase in amplitude per percent increase in contrast).

“Contrast gain control” is a phenomenological term that refers to a nonlinearity in the system associated with a speeding up of the neural response as contrast increases. Strictly speaking, the integrative time constant of the system decreases as contrast increases. A consequence of this change in time constant is curvilinear behavior in the relations of amplitude and phase of the response with contrast – the amplitude vs. contrast function exhibits compression (i.e., a decrease in the slope of the function as contrast increases) and the phase (relative timing) of the response vs. contrast function advances with contrast. The concept of contrast gain control was introduced by Shapley and Victor, ^2,3 and it has been shown to be a characteristic of retinal ganglion cells of cat ^2,3 and monkey ⁴, magnocellular dorsal lateral geniculate nucleus (LGN) cells of monkey ⁴ and cortical cells of cat ^5,6 and monkey ^7,8. Contrast response functions from adult humans have been shown to exhibit strong contrast gain control. ⁹ One goal of the current study was to obtain contrast response functions from infants and compare them to functions obtained from older observers.

Contrast-dependent visual evoked potentials (VEPs) to positive-contrast and negative-contrast stimuli obtained from children have previously been shown to differ from those of adults in both amplitude and phase. ¹⁰ Behavioral and VEP studies of contrast sensitivity indicate that the human visual system is immature at birth, develops rapidly during the first year of life, and continues to develop throughout childhood. ^{11,12,13,14,15,16,17,18,19,20} In general, the peak of the contrast sensitivity function shifts to higher spatial and temporal frequencies, and there is an increase in peak sensitivity with age. Behavioral and VEP studies also show that grating acuity develops beyond the first year of life. ^{17,18,19,21,22,23,24,25,26,27} In comparison to adults, spatial functions of infants exhibit larger amplitudes and relatively small changes in phase with increases in spatial frequency. ²⁷ These findings complement anatomical evidence that indicates significant maturational changes occur at the level of the retina, ^28,29,30 the lateral geniculate nucleus, ^31,32 and primary visual cortex. ^32,33,34

A nonlinear model based on shunting inhibition has been proposed to explain the contrast gain control observed in cortical responses from simple cells in macaque monkeys. ⁷ Zemon and Gordon ⁹ used a biophysical model which incorporates shunting inhibition to characterize the contrast gain control in contrast response functions obtained with the VEP in human adults. A second goal of the current study was to apply this biophysical model to quantify the contrast response functions in infants.

To our knowledge, the current study is the first to examine monocular contrast response functions in human infants. Monocular assessment of these functions may be of clinical relevance for conditions that cause a monocular loss of contrast sensitivity, such as amblyopia.³⁵

METHODS

Participants

Twenty-nine typically-developing human infants ranging from 15 to 28 weeks of age (11 females, 18 males), two children (a 3-year-old male and a 10-year-old female), one 14-year-old adolescent (female), and nine adults (20–39 years, all females) were recruited for this study. Most infants were recruited through The New York Presbyterian Hospital-Weill Medical College of Cornell University. Some infants, children and adults were also recruited by word of mouth or through notices posted on bulletin boards near the Psychology Department offices at Hunter College, City University of New York. This research followed the tenets of the Declaration of Helsinki, and it was approved by the Institutional Review Boards at Hunter College and The New York Presbyterian Hospital-Weill Medical College of Cornell University. This project also complied with HIPAA (Health Insurance Portability and Accountability Act) privacy regulations. Written consent was obtained from all adults and parents of all infants and children tested. In addition, oral consent was obtained from children younger than 12 years of age, and written assent from children older than 12 years of age.

Stimuli

An Enfant system (Neuroscientific Corp.) was used for presenting stimuli and recording electrophysiological responses. A Nokia monitor (Multigraph 447X) was used as a stimulus display, and it had a mean luminance of 78 cd/m². At the viewing distance of 57 cm, the stimulus field was 20 deg. A contrast sweep technique was used. Sweep VEPs have been obtained previously to assess the maturation of spatial mechanisms in infants. ^25,27 The stimulus conditions considered in this study included contrast sweeps at two spatial frequencies: 0.75 and 1.5 c/deg. Horizontal square-wave gratings were contrast reversed with a square-wave modulation signal at 7.5 Hz (synchronized to the frame rate of the display.) The duration of a run was approximately 8.5 seconds. The depth of luminance modulation (Michelson contrast) of the gratings increased in seven octave steps from 1–64% with an initial step at 0%. (Here, depth of modulation and contrast are synonymous and are used interchangeably.) There were 64 frames per step (8 frames per cycle), and each step was approximately 1 s in duration. The frame rate of the display was approximately 60 Hz.

VEP Recording

For all VEP recording sessions, the same three electroencephalographic (EEG) electrode placements were used. These placements are based on the International 10–20 System, ³⁶ and standard gold-cup electrodes were attached to these midline sites. One electrode at Oz (positive lead; located at 10% of the distance from the inion to the nasion) was referenced to another one at Cz (negative lead; at 50% of the distance from the inion to the nasion) with a floating ground electrode placed at Pz (at 30% of this distance).

Optically-isolated differential amplifiers were used to enlarge the EEG signal 10,000 times and bandpass filter the signal with a low- and a high-frequency cut-off of 0.5 Hz and 100 Hz respectively (6 dB/octave roll-off). The signal was then digitized by an analog-to-digital converter and stored in a PC/AT compatible computer. A rectangular EEG analysis window was used. ²⁷ The size of the window was equal to the duration of a step. Five EEG samples were taken per frame (synchronized to the frame rate of the display), which yielded a total of 320 samples per step.

Analysis of the VEP

Steady-state VEPs were analyzed by a discrete Fourier transform to derive the amplitudes and phases of frequency components that occur at multiples of the stimulus frequency. These are the only driven components in the VEP to such an input signal. The dominant (second harmonic) component of interest in this study occurs at twice the stimulus frequency. In the analysis, response phase is defined relative to a cosine reference signal. Thus, even though the stimulus modulation signal is in sine phase, a response component in sine phase yields a phase angle of - 90 deg.

The T² _circ statistic ³⁷ which was specifically designed for the analysis of variability in Fourier components of the VEP was used to estimate 95% confidence regions about the mean vector response. Vector-mean amplitude and phase values along with corresponding 95% confidence regions were plotted vs. depth of modulation. Phase data that were determined to be in the noise were excluded from the plots.

The Nonlinear Model

A biophysical model developed by Zemon and Gordon ⁹ was used to fit jointly the amplitude and phase measures of the responses. A nonlinearity incorporated into the model to explain the curvilinear behavior in the contrast response functions was based on the neurophysiological mechanism of shunting inhibition. This form of inhibition was first described by Fatt and Katz.³⁸ The term refers to the fact that a fraction of the excitatory current entering through open ion channels in the plasma membrane of a neuron is shunted out of the cell through neighboring ion channels, ³⁹ which appear to be controlled by the inhibitory neurotransmitter γ-aminobutyric acid (GABA).⁴⁰ Model fits yield estimates of the following four free parameters: initial membrane conductance, initial phase, coefficient of shunting inhibition, and threshold depth of modulation. Then, the system’s integrative time constant can be computed (for details about the model, see Appendix (available online at www.optvissci.com), also Zemon & Gordon⁹). Here, plots of time constant vs. depth of modulation are given along with the amplitude and phase data to illustrate the model’s behavior over the range of depths of modulation used. (These time constant plots are not used to extrapolate the observers’ responses below the noise level.)

Initial conductance of the system, g_o, is a measure of initial contrast gain, and the main determinant of the initial slope of the function. The shunting coefficient, m, determines the magnitude of shunting conductance at a given contrast level, and therefore, it is a measure of contrast gain control, which determines the magnitude of amplitude compression and phase advance. ϕ_o is the initial phase of the second harmonic response (response phase excluding any contrast-dependent phase change). d_o is the threshold depth of modulation, and a negative d_o is indicative of high spontaneous activity at the frequency component in the EEG. η² is the proportion of total variance in the data explained by the model fit. τ₁ is the time constant at 1% contrast and τ₃₂ is the time constant at 32% contrast.⁹

The application of this model to the VEP implies a close correspondence between the properties of single neurons and the extracellular signals that produce the scalp potentials known as the VEP. This gross response measure is thought to reflect the net extracellular current flow generated by a large number of neurons primarily in the superficial layers of visual cortex. ^41,42 The most numerous cells in the neocortex are the pyramidal neurons in layers 2/3, ⁴³ and apical dendrites of pyramidal neurons are the main neuronal structures in the superficial layers of cortex. Apical dendrites possess the dipole-like properties required of an evoked potential generator ^42,44 There is evidence to indicate that both excitatory and inhibitory postsynaptic potentials contribute to the net extracellular currents that generate the VEP. ^42,45 The linear sum of these extracellular currents are expected to reflect the membrane properties of the neuronal structures (i.e., apical dendrites) that produce them, and therefore, the VEP, as a scalp manifestation of this activity, is expected to reflect these membrane properties as well.

The fitting procedure is based on the Generalized Reduced Gradient (GRG2) Algorithm for optimizing nonlinear problems developed by Leon Lasdon and Allan Waren. ⁴⁶ This algorithm is incorporated in Microsoft Excel Solver and a least-squares criterion is used to fit the data. Local minima in the fitting procedure were avoided by first estimating values of the free parameters to give an approximate fit to the data, based on visual inspection, and then running the Solver algorithm. No constraints were placed on the four free parameters.

In some observers, the amplitude of the response decreased at the highest contrast level tested. The model, however, can only produce monotonically increasing functions, and therefore, in these cases, the last datum at the highest contrast was not included in the fitting procedure. Data that fell initially into the noise range, however, were included.

Procedures

Observers were tested in a dark room. Infants sat on their parent’s laps to view the stimuli. The electrical activity of the brain was recorded using electrodes attached to the scalp with water-soluble paste. Contrast sweeps were performed during a single one-hour session (which included time for breaks.) Ten runs were collected from each participant under each stimulus condition. Infants viewed the stimuli first monocularly, and, if time permitted, infants viewed the stimuli binocularly. (Only the monocular data are reported here.) During monocular testing, one eye was covered with a soft non-transparent eye patch. In approximately half of the infants, the right eye was tested first; in the other half the left eye was tested first.

One person attracted the infant to focus on the stimuli with the aid of a small toy dangling in the center of the display screen. Another person initiated stimulation, recorded the data file information on a sheet, and stored the data on the computer.

RESULTS

Not all participants were run under all conditions. Of those tested at a spatial frequency of 0.75 c/deg (22 infants, one 10-year-old, one 14-year-old and nine adults), one infant and two adults consistently did not produce reliable responses above the noise level, and therefore, they were excluded from subsequent analyses.

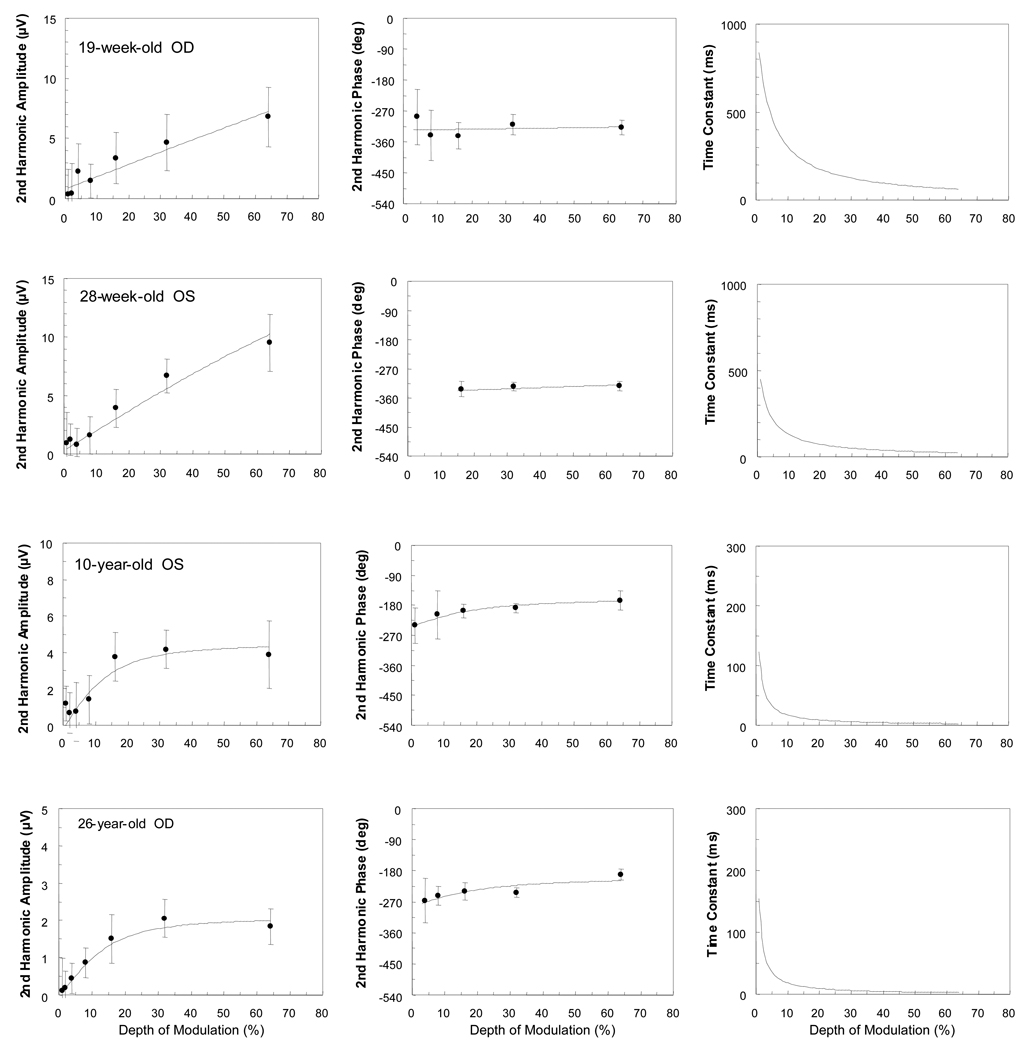
Second harmonic amplitude and phase data as a function of depth of modulation for a 19-week-old, a 28-week-old, a 10-year-old and a 26-year-old observer at the 0.75 c/deg condition are displayed in Figure 1. Corresponding time constants are also plotted in this figure. The model’s parameter estimates for each of these data sets are shown in Table 1.

Figure 1.

Amplitude and phase of second harmonic responses and corresponding time constants as a function of contrast (depth of modulation) for the 0.75 c/deg condition. The lines represent the best model fits obtained using the amplitude and phase of the response jointly. Data from a 19-week-old, a 28-week-old, a 10-year-old, and a 26-year-old are shown. Each participant’s age and eye tested are indicated. Note the different amplitude and time constant scales for the different observers. Error bars represent 95% confidence limits.

Table 1.

Model’s parameter estimates for each of the data sets plotted in Figure 1 and Figure 3.

Spatial Frequency	Participant	go (µS/cm2)	ϕo (deg)	do (%)	m (µS/cm2/%)	η2	τ1(ms)	τ32(ms)
0.75 c/deg	19-week-old	0.77	−237	−7.93	0.19	0.93	836.16	118.48
	28-week-old	1.29	−254	−1.63	0.49	0.96	449.48	46.93
	10-year-old	2.02	−153	0.78	4.51	0.92	122.37	5.46
	26-year-old	0.89	−193	0.57	4.27	0.91	155.12	5.81
1.5 c/deg	21-week-old	1.29	−305	−3.85	0.51	0.97	443.98	45.08
	3-year-old	0.48	−156	−7.38	1.17	0.95	484.19	21.06
	26-year-old	3.33	−231	1.51	14.72	0.94	44.33	1.69

g_o: initial specific conductance in the system, ϕ_o initial phase, d_o threshold depth of modulation, m: shunting coefficient, η² proportion of total variance in the data accounted for by the model fit, τ₁ time constant at 1% depth of modulation and τ₃₂ time constant at 32% depth of modulation

There are striking differences between the contrast functions of the infants and the functions of the 10- and 26-year-olds. The functions from infants are nearly linear: they show little amplitude compression and phase shift with increases in depth of modulation. In general, response amplitudes from infants are larger than those from adults. (Note that the amplitude and time constant scales differ from panel to panel.) Both the 10-year-old and the 26-year-old exhibit contrast gain control (amplitude compression and phase advance) with increases in depth of modulation. For the infants, the values of the shunting coefficient (m) are below one, whereas for the older observers, they are around four. Infants yield longer time constants than do adults. Here, time constant values decrease with increasing depth of modulation in both infants and adults. In the 10- and the 26-year-olds, there is a greater than 20-fold decrease in time constant, whereas in the infants there is less than a 10-fold decrease over the range of contrasts calculated (1–32%). The infants’ functions are nearly linear, however, and therefore their data sets could have been fitted well with the shunting coefficient (m) set to zero, which would have resulted in a straight amplitude plot, phase invariance, and no change in time constant as a function of contrast. There were no constraints, however, placed on this or any other parameter in the model.

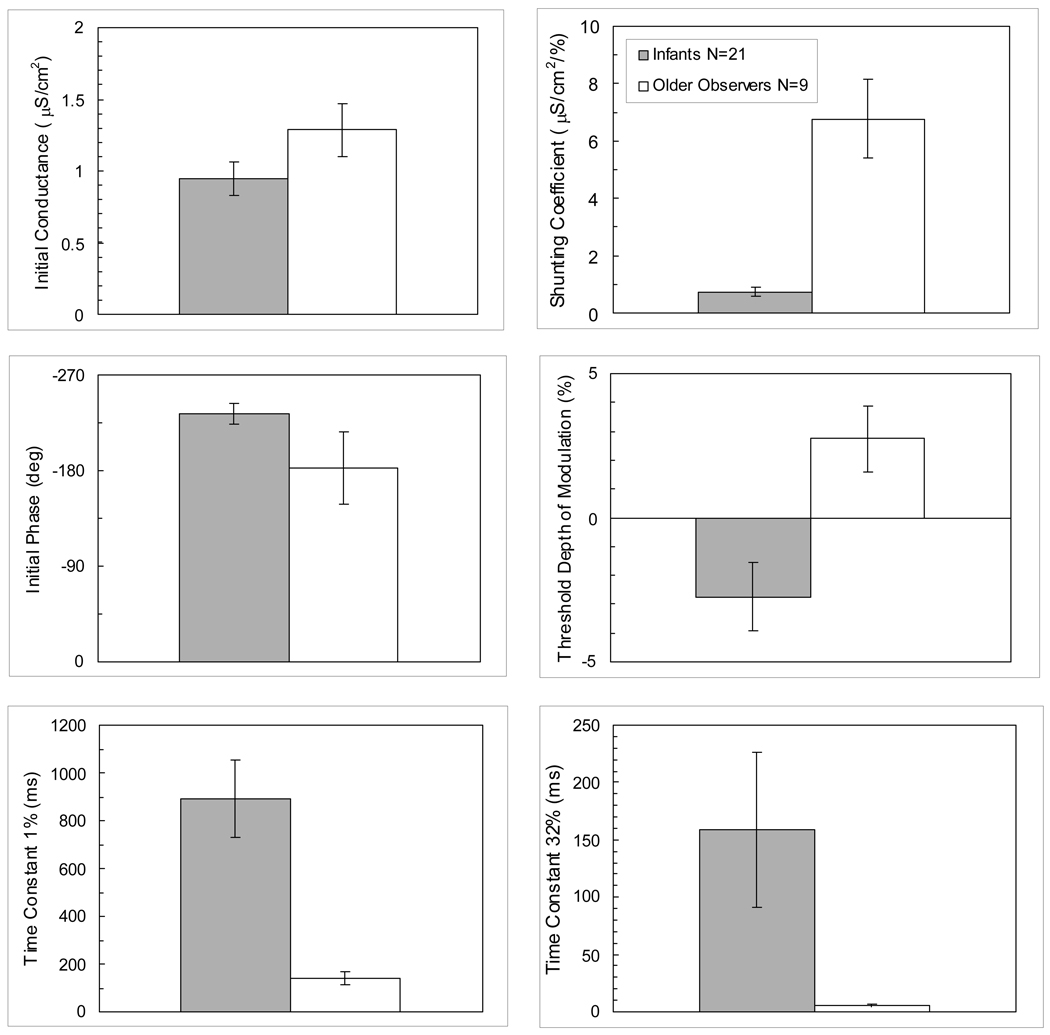
Figure 2 shows bar graphs of the mean values of the parameters and time constants for the 0.75 c/deg condition in infants and older observers. The 10- and the 14-year-olds had similar parameter estimates as the adults and were therefore included in the group of older observers. One set of monocular data was selected from each observer – whichever set had the greater amount of variance accounted for by the model with at least three pairs of points above the noise level (established by the 95% confidence region). The mean amount of variance accounted for by the model for each age group was 90%.

Figure 2.

Bar graphs of the model’s mean parameter values for each age group (infants and older observers) obtained from the best eye of each observer for the 0.75 c/deg condition. Error bars represent ±1 SEM.

For the shunting coefficient and resulting time constants, negative values were occasionally obtained, which have been explained in terms of negative conductance in the system. ⁹ In these cases, absolute values were used to compute means for the group. Mean values for the shunting coefficient in infants and adults were 0.74 µS/cm²/% (±0.15 SEM) and 6.78 µS/cm²/% (±1.36 SEM) respectively. There are prominent differences between infants and older observers for the shunting coefficient (unequal variance t(8.2) = 4.43, 2-tail p =.002) and the time constants at both 1% (unequal variance t(21.1) = 4.54, 2-tail p <0.001) and 32% (unequal variance t(20.0) = 2.28, 2-tail p =0.03) depths of modulation. Infants have higher mean values for corresponding time constants than do older observers. Time constant mean values at 1% and 32% depth of modulation were 890.3 ms (±162.9 SEM) and 158.8 ms (±67.3 SEM) respectively in infants versus 140.3 ms (±27.5 SEM) and 5.2 ms (±1.2 SEM) in older observers. The decrease in the time constant from 1 to 32% depth of modulation is larger in the older participants than in infants. The ratio of the mean absolute time constants at 1% and 32% depths of modulation for infants is relatively small (5.6) compared to that for older observers (27.2).

The initial conductance and initial phase parameters do not differ significantly between infants and older observers (unequal variance t(14.5) = 1.56, 2-tailed p = 0.14; unequal variance t(9.4) = 1.46, 2-tailed p = 0.18 respectively). Initial conductance mean values were 0.94 µS/cm² (±0.11 SEM) and 1.28 µS/cm² (±0.18 SEM) in infants and adults respectively. Mean values for initial phase in infants and adults were −233.76 deg (±9.76 SEM) and −182.45 deg (±33.80 SEM) respectively. Phase data at high contrasts, however, are quite different between the groups. At the highest contrast tested, 64%, older observers were advanced in phase relative to infants by more than 100 deg. The threshold depth of modulation parameter is different between these two groups, with a negative mean value for infants (−2.76 % ±1.19 SEM) and a positive value (2.75 % ±1.15 SEM) for older observers (unequal variance t(23.5) = 3.33, 2-tail p =0.003). In the restricted age range of infants tested (19–28 weeks), there were no significant correlations in the model parameters with age (r ranged from 0.07 to 0.27, 2-tailed p> .05).

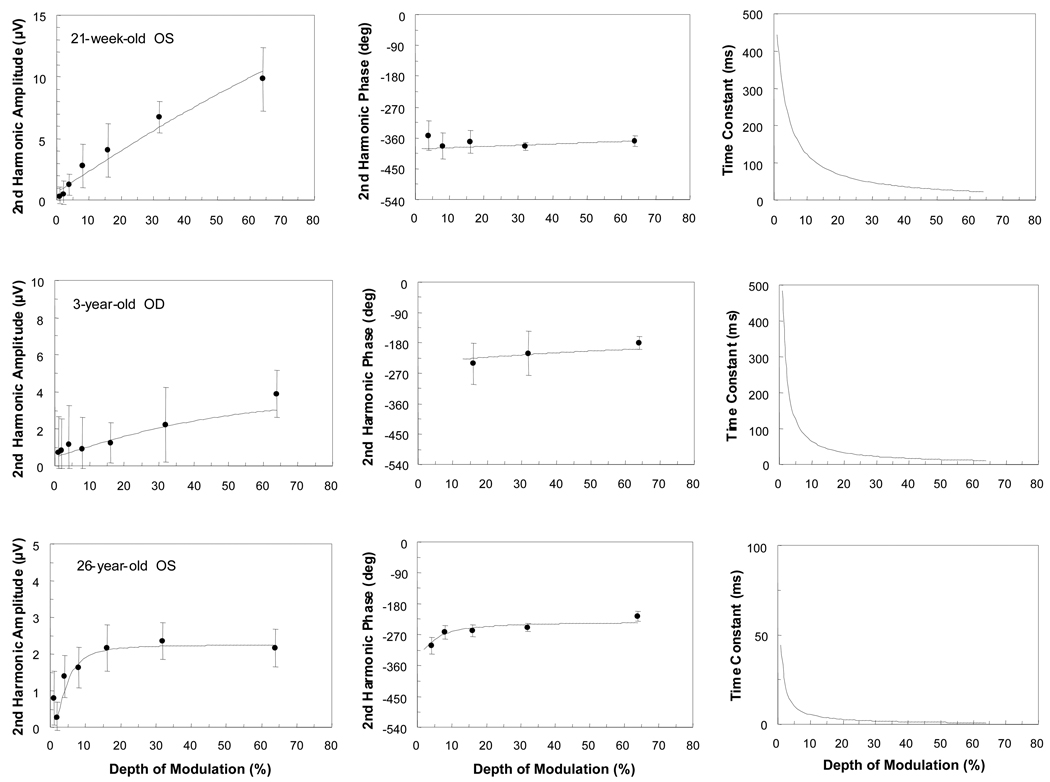
Preliminary data were also collected under the 1.5 c/deg condition for seven other infants, a 3-year-old, and the same 10-year-old, 14-year-old and nine adults tested with the 0.75 c/deg condition. Five of the seven infants and nine of the 12 older observers yielded responses adequate to be fitted by the model. Figure 3 shows data for a 21-week-old, a 3- and a 26-year-old tested under the 1.5 c/deg condition. The pattern observed in these data is similar to the one seen when participants were tested under the 0.75 c/deg condition (Figure 1). Again, there are marked differences between the contrast functions of infants and older observers. The response from the 21-week-old is nearly linear. The model fit to the data from the 3-year-old exhibits increased characteristics of contrast gain control (amplitude compression and phase advance with depth of modulation) as compared to that from the infant. The shunting coefficient is greater for the 3-year-old (m=1.17) than for the infant (m=0.51), but it is considerably weaker than that for the adult (m=14.72). The 26-year-old exhibits a steep slope in the amplitude function at low contrasts with near saturation by 16% depth of modulation. Also, this observer exhibits a steep phase advance with increases in depth of modulation. Again, the time constants decrease with increasing depth of modulation over the range tested. Here, there is approximately a 10-fold decrease in the infant’s function, whereas the decrease is more than 20-fold in the 3- and the 26-year-olds’ functions. The shunting coefficients range from nearly zero (0.16) in the 16-week-old’s data to a high value of 14.72 in the 26-year-old’s data.

Figure 3.

Amplitude and phase of second harmonic responses and corresponding time constants as a function of contrast (depth of modulation) for the 1.5 c/deg condition. The lines represent the best model fits obtained using the amplitude and phase of the response jointly. Data from a 21-week-old, a 3-year-old and a 26-year-old are shown. Each participant’s age and eye tested are indicated. Note the different amplitude and time constant scales for the different observers. Error bars represent 95% confidence limits.

DISCUSSION

This study explored the development of contrast mechanisms from infancy through adulthood. One key finding is that contrast-response functions in infants 15–28 weeks of age are nearly linear whereas the more mature visual systems produced functions with notable nonlinear characteristics of contrast gain control (amplitude compression and relative phase advance with increases in depth of modulation). Given that contrast gain control has been attributed to the presence of shunting inhibitory synapses on the neuronal membrane, ⁷ a nonlinear model based on shunting inhibition ⁹ was used to quantify both the amplitude and phase data with four free parameters and estimate the integrative time constant of the system as a function of contrast.

Shunting inhibition appears to have a divisive effect on subthreshold excitatory postsynaptic potentials. ^47,48 It is mediated by GABA_A receptors, and via this mechanism, increases in contrast result in increases in cellular conductance and, consequently, decreases in the integrative time constant of the system. ^9,40 The model used in the present work was applied principally to estimate the magnitude of shunting inhibition in infants and to investigate the developmental time course of this mechanism. In this model, shunting conductance is linearly related to depth of modulation. The much lower value (nearly zero) of the shunting coefficient (m) in infants (up to 28 weeks of age) as compared to older observers, and the corresponding lack of contrast gain control in infants, indicates that this inhibitory process matures later than early infancy.

Strong contrast gain control effects are found in the visual cortex of cats, ^5,6 monkeys, ^7,49 and humans. ⁵⁰ Thus, the maturational effects observed in this study may be cortical in origin, which is consistent with previous developmental work.¹⁰

Additional studies support the view that cortical inhibition increases with age. In one VEP study, Morrone and Burr ⁵¹ examined cross-orientation inhibition in infants over a period of eight months and concluded that multiplicative (divisive) attenuation was not evident before six months of age. By ten months of age, the response characteristics were similar to those in adults. In another VEP study of human infants, Sokol, Zemon, and Moskowitz ⁵² showed that nonlinear lateral interactions that are presumably of GABAergic origin were not manifested in the responses until infants reached the age of about six months. In addition, Murphy, Beston, Boley, and Jones ⁵³ studied the expression of glutamatergic receptors and GABA_A receptors in human primary visual cortex during the first five years of life. They noted that expression of GAD65, a GABA synthetic enzyme found mainly in axon terminals, increased significantly by one to three years of age. In future work, it would be of interest to examine the effects of drugs that modulate GABAergic activity, such as benzodiazepines ^54,55 or certain antiepileptic medications (e.g., gabapentin ^56,57) on the contrast response functions of adults. These studies might elucidate further the mechanisms underlying contrast gain control. In a recent study, administration of gabapentin (which is thought to elevate GABA-mediated inhibition) to patients with epilepsy resulted in enhancement of lateral interactions in the VEP that are attributed to GABA-mediated intracortical inhibition.⁵⁷

In the model, the integrative time constant is computed as the ratio of system capacitance to total system conductance. Thus, as shunting conductance increases with depth of modulation, the total conductance (initial conductance plus shunting conductance) increases and the time constant decreases. This change in time constant was quantified here by computing the ratio of time constant values obtained at 1% and 32% depth of modulation. In a few cases, total conductance in the model fit was negative as a result of a negative shunting coefficient, and therefore, the time constant estimates were negative as well. Negative conductance with respect to this model has been obtained in previous work, ⁹ and in that study it was pointed out that this result has been observed at the cellular level and is associated with NMDA-receptor function. ⁵⁸ Here, we were interested in the magnitude and change in temporal integration in the system, and therefore, we used the absolute values of the shunting coefficient and time constants in the analysis. In some cases (i.e., when the shunting coefficient was zero), infants exhibited no change in time constant with contrast. On average, however, this ratio was about 5 for infants and about 27 for older observers tested at 0.75 c/deg. At a given contrast level, infants’ time constant values were considerably longer than those measured in older observers. This finding is consistent with developmental changes in temporal integration reported for neurons of infant monkeys. ⁵⁹ Larkum et al. ⁴³ examined synaptic integration in pyramidal neurons from layers 2/3 in rat neocortical slices using dual somatic and dendritic whole-cell (patch-clamp) recordings. They obtained membrane time constants of about 8 ms for both dendritic and somatic sites. These estimates are consistent with our estimates of time constants at high contrasts in older observers.

The initial conductance (g_o) parameter (which is a measure of the contrast gain of the system) as measured with the model did not change much with age for the 0.75 c/deg condition. Thus, the initial slopes of the amplitude vs. depth of modulation functions were similar for infants and older observers. This might indicate that the excitatory input to the visual cortex is about the same for these two age groups. VEP amplitudes from infants, however, are considerably larger at high contrasts than are respective amplitudes from adults. This finding appears to be a result of the lack of contrast gain control in the infant visual system.

The initial phase parameter, ϕ₀, is the measure of phase shift in the response prior to any phase change induced by contrast modulation, and it is mostly associated with transmission delay in the system. ⁹ In this study, there was no significant difference in this parameter value for infants and older observers. At high contrasts, however, there is a sizeable phase difference between the groups, with the older observers advanced in phase relative to the infants. This separation in response phase is the result of the contrast gain control phenomenon of phase advance with increases in contrast that is present in the mature visual systems. The large phase difference between the groups found at high contrasts is consistent with that reported for infant vs. adult data collected under comparable spatial and temporal frequency conditions in previous work. ²⁷ It should be noted that an alternative explanation for phase shifts related to changes in contrast level is a change in the relative contributions from excitatory and inhibitory activity to the VEP.¹⁰

The final free parameter in the model, threshold depth of modulation, was significantly different between the two age groups, with infants yielding negative values and older observers yielding positive values. The finding of lower (negative) thresholds in infants is a paradoxical result which may be due to elevated spontaneous activity at the response frequency (15 Hz). This greater level of activity without stimulation may be a consequence of reduced intracortical inhibition in the infant visual system. The presence of spontaneous activity, or noise in the recording, prevents the use of the threshold parameter to estimate an observer’s contrast sensitivity.

The nonlinear mechanism of contrast gain control is also present in the precortical magnocellular stream, but it is not present in the precortical parvocellular stream. The magnocellular pathway, which originates in the retina and projects to the two ventral layers of the LGN, exhibits high contrast sensitivity whereas the parvocellular pathway, which also originates in the retina but projects to the four dorsal layers of the LGN, exhibits low contrast sensitivity. ⁶⁰ The nearly linear response functions obtained from infants are similar to those obtained from neurons in parvocellular-projecting ganglion cells and parvocellular neurons in the LGN of primates. ^4,60 The contrast response functions obtained from children and adults are similar to the functions obtained from magnocellular-projecting ganglion neurons and magnocellular neurons in the LGN: ^4,60 they exhibit the nonlinear effects of amplitude compression and phase advance with increasing contrast. Thus, an alternative explanation for the present results is that there is a relatively greater input from the parvocellular pathway in early infancy (due to differential maturation of the magnocellular and parvocellular systems), and that difference could contribute to the more linear responses obtained from infants. Hickey ³¹ studied the postnatal development of neurons in magnocellular and parvocellular layers of the human LGN and discovered different time courses for cellular growth in these two populations of neurons. Parvocellular neurons had a rapid growth phase ending at about six months and a more gradual growth phase during the subsequent six months, whereas, magnocellular neurons increased rapidly in size for one full year and then continued to increase gradually for another year. Thus, although the evidence discussed above supports a dominant cortical contribution to the developmental changes reported here, additional research is needed to determine the extent of retinal, LGN, and cortical contributions to the maturational effects observed in these contrast response functions.

There are major anatomical changes in the visual system throughout infancy and childhood, and these changes are reflected in behavioral and VEP data. The contrast response functions obtained in this study show developmental alterations that are consistent with increased shunting inhibition with age. Thus far, these functions have been examined under limited spatial and temporal conditions. It would be worthwhile, in future work, to explore the dependence of these functions and the model parameters on a wide range of spatiotemporal conditions. The VEP technique described here may prove to be a sensitive tool to measure the strength of contrast gain control (level of shunting inhibition) and the time constant for neural integration in humans.

APPENDIX

Nonlinear Model

The nonlinear model ⁹ applied here to fit the amplitude and phase data of the VEP contrast response functions is based on the physiological mechanism of shunting inhibition that occurs at a cellular level. A conductance change across the cellular membrane associated with the opening of shunting inhibitory ion channels results in a change in the transfer characteristics and integrative time constant of the system. In the model, the shunting conductance (g_s) is assumed to be linearly related to the stimulus contrast (depth of modulation, D). The total integrative time constant for the system (τ) is given by:

$$\tau =\frac{C}{g_0+g_s}=\frac{C}{g_0+m(D-d_0)}$$

where g₀ is the initial specific conductance of the system (i.e., membrane conductance in the absence of stimulation and 1^st free parameter in the model), C is the specific capacitance of the cellular membrane (assumed to be 0.8 µF/cm²), m is the shunting coefficient (constant of proportionality and 2^nd free parameter), which is used as a measure of strength of shunting inhibition, and d₀ is the threshold depth of modulation required to open the shunting ion channels (3^rd free parameter). This parameter is used to explain a clear threshold effect (rightward shift of the contrast response function along the depth of modulation axis) observed in some data sets, and elevated activity at the relevant (second harmonic) frequency in the EEG without stimulation (leftward shift of the contrast response function along the depth of modulation axis) observed in other data sets.

A shunting effect was first noted for the crustacean nerve-muscle synapse by Fatt and Katz.³⁸ More recently, Borg-Graham et al. ⁴⁰ have shown that, in cat primary visual cortex, stimulus-driven conductance change is associated with shunting inhibition at γ–aminobutyric acid (GABA_A) receptor-mediated synapses.

The model’s differential equation yields the system’s frequency response, which in turn yields the model’s estimates of amplitude and phase of the relevant (second harmonic) frequency component in the response, given below:

$$\begin{array}{ll}\mathit{\text{Response}}\mathit{\text{Amplitude}}\hfill & A_R=(D-d_0)\left(k\frac{g_0/C}{\sqrt{p^2+{\omega }^2}}\right)\hfill \\ \mathit{\text{Response}}\mathit{\text{Phase}}\hfill & {\varphi }_R=\varphi +{\varphi }_o\hfill \end{array}$$

where p is the reciprocal of the total integrative time constant:

$$p=\frac{g_0+g_s}{C}=\frac{1}{\tau }$$

and ω is the angular temporal frequency of the relevant response component (in radians/second), K is a gain setting (which is fixed at a value of 10 for all fits because this value was found empirically by Zemon and Gordon ⁹ to yield good fits across observers and conditions and provide physiologically plausible values for initial specific conductance), ϕ_o is initial phase (the 4^th and final free parameter in the model), and ϕ is given by:

$$\varphi =-{\text{tan}}^{-1}\left(\frac{\omega }{p}\right)$$

For each contrast response function, an algorithm based on the Generalized Reduced Gradient (GRG2) nonlinear optimization code (developed by Leon Lasdon and Allan Waren ⁴⁶) and incorporated in Microsoft Excel Solver is used with a least-squares criterion to fit the model to the second harmonic cosine and sine coefficients that result from applying a discrete Fourier transform to the EEG data. The model estimates for these coefficients were calculated from the response amplitude and phase equations given above as follows:

$$\begin{array}{l}\text{Cosine}\text{coefficient}={\mathrm{A}}_{\mathrm{R}}•\text{cos}(\mathrm{\varphi }\mathrm{R})\\ \text{Sine}\text{coefficient}={\mathrm{A}}_{\mathrm{R}}•\text{sin}(\mathrm{\varphi }\mathrm{R})\end{array}$$

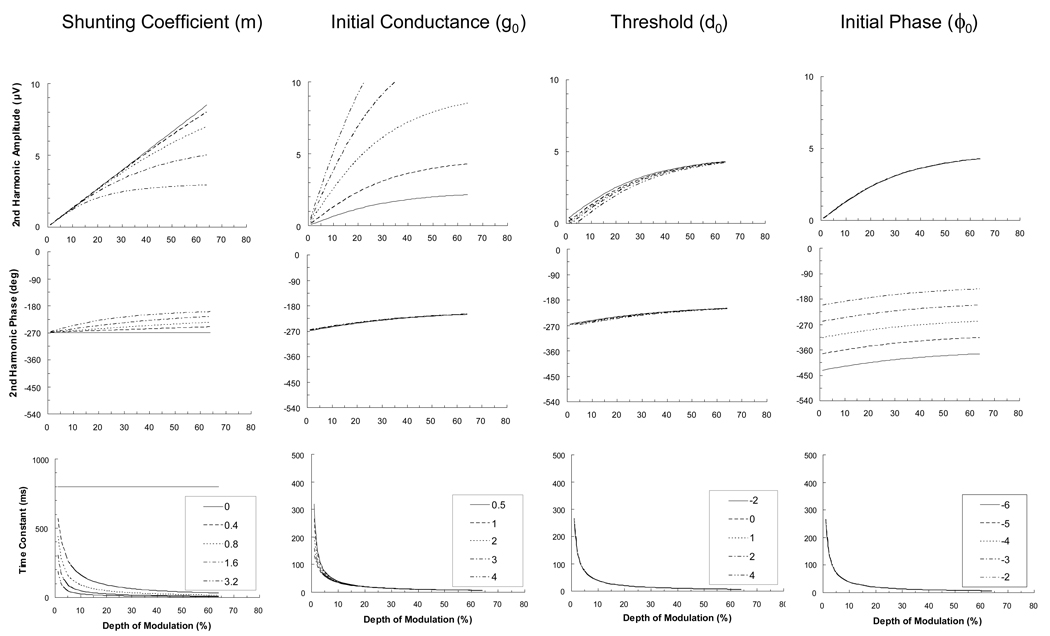
Figure 4 depicts the effects of varying each of the model’s parameters on amplitude, phase, and the computed time constant. (The initial parameter values were set as follows: m = 2 µS/cm²/%, g₀ = 1 µS/cm², d₀ = 0 %, ϕ₀ = − π rad). It is clear that increases in the value of the shunting coefficient (m) results in increases in amplitude compression and phase advance, in addition to a shortening of the system’s time constant. When this coefficient is set to zero, the amplitude function is linear and phase and time constant plots are invariant, with a time constant of 800 ms over the entire range of depth of modulation. The main effect of manipulating initial conductance, g₀, is a change in initial slope (contrast gain) of the amplitude function. The main effect of manipulating the threshold depth of modulation, d₀, is to translate the amplitude function along the depth of modulation axis. The manipulation of initial phase, ϕ₀, is simply to translate the phase function along the phase axis.

Figure 4.

Model plots of second harmonic amplitude, phase, and time constant. These plots show simulations of the effect of changing one of the four free parameters (shunting coefficient, m; initial conductance, g₀; threshold, d₀; and initial phase, ϕ₀) while keeping the others fixed. Parameter values manipulated in the simulations are shown in the legend box. Units for the four parameters are as follows: m (µS/cm²/%), g₀ (µS/cm²), d₀ (%), ϕ₀ (rad). The first column of plots shows the effects of varying m. When m is equal to zero, the amplitude function is linear, the phase function is invariant, and the time constant is invariant at 800 ms. With larger values of m, the plots show more curvilinear behavior (amplitude compression, phase advance, and decreasing time constant). The second column shows the effects of changing g₀. Increasing g₀ affects mainly the amplitude plots, increasing the slope (initial contrast gain) of the function. The third column illustrates that increasing d₀ shifts the amplitude curve to the right. The last column demonstrates that increasing ϕ₀ produces an upward shift of the second harmonic phase plot.