Skip to main content
PMC home page
BMC Neurology logoLink to BMC Neurology
. 2010 Apr 26;10:26. doi: 10.1186/1471-2377-10-26

The Subjective Index for Physical and Social Outcome (SIPSO) in Stroke: investigation of its subscale structure

Paula Kersten 1,✉, Ann Ashburn 1, Steve George 2, Joseph Low 3
PMCID: PMC2873322  PMID: 20420687

Abstract

Background

Short and valid measures of the impact of a stroke on integration are required in health and social settings. The Subjective Index of Physical and Social Outcome (SIPSO) is one such measure. However, there are questions whether scores can be summed into a total score or whether subscale scores should be calculated. This paper aims to provide clarity on the internal construct validity of the subscales and the total scale.

Methods

SIPSO data were collected as part of two parallel surveys of the met and unmet needs of 445 younger people (aged 18-65) with non-recent stroke (at least one year) and living at home. Factor, Mokken and Rasch analysis were used.

Results

Factor analysis supported a two factor structure (explaining 68% of the variance) as did the Mokken analysis (overall Loevinger coefficient 0.77 for the Physical Integration subscale; 0.51 for the Social Integration subscale). Both subscales fitted the Rasch model (P > 0.01) after adjusting for some observed differential item functioning. The 10-items together did not fit the Rasch model.

Conclusions

The SIPSO subscales are valid for use with stroke patients of working age but the total SIPSO is not. The conversion table can be used by clinicians and researchers to convert ordinal data to interval level prior to mathematical operations and other parametric procedures. Further work is required to explore the occurrence of bias by gender for some of the items.

Background

Between 174 and 216 people per 100,000 per year suffer a stroke in the UK[1]. Of these about a third will have long-term disability[2]. The advent of better treatment, such as thrombolysis and improvements in acute rehabilitation services, means that more people will survive a stroke. A good quality of life after stroke, maximising independence, well-being and choices, is therefore an important focus for rehabilitation services [3,4]. Measuring such outcomes can be carried out by health care professionals, using tools such as the Barthel Index or the National Institutes of Health Stroke Scale. However, the impact of a stroke upon an individual's life is more appropriately measured by patients themselves. A candidate measure for this area of interest is the Stroke Impact Scale (SIS), which contains a domain measuring social participation [5], but also seven other domains. Thus, the SIS is rather long, placing significant burden on the participant in terms of completion. A much shorter scale, the Subjective Index of Physical and Social Outcome (SIPSO) (10 items) has a focus on physical and social integration after a stroke. The SIPSO was developed using extensive qualitative work [6] and validity and reliability has been shown to be good, when examined with traditional psychometric methods [7-9]. The SIPSO is much shorter than health status measures frequently used in stroke[10]. Thus, this shorter stroke specific measure is worthy of further exploration for use in clinical practice and research. The measure has been used in studies exploring unmet needs amongst people with stroke [11,12], the benefits of a community based exercise and education intervention [13] and a community ambulation intervention[14]. Although the scale has been shown to consist of two subscales, a physical and a social integration subscale [8], the originators have also proposed that a total score can be used[9]. They base this on a somewhat lower Cronbach alpha for the Social Integration subscale, even though this is acceptable for individual use (0.82) and somewhat lower correlations for items 6 and 10 with this subscale (though acceptable with correlation values of 0.67 and 0.74 respectively and greater than the correlation with the physical integration subscale). Items 6 and 10 measure how often someone feels bored and how s/he feels about appearing in public. Thus, there is a conflict between earlier statements that the scale consist of two subscales [8,9] and that the SIPSO also can be used in its totality [9] and at present total SIPSO scores are used in research [13,14]. Further, researchers use parametric analyses to analyse SIPSO data. Since the measure produces ordinal data it would be of use if an interval transformation could be produced. Interval transformations can be produced if the scale fits the Rasch model.

Rasch analysis is useful in testing whether items from a scale measure a unidimensional construct [15,16], which is required to justify the summation of scores. Rasch analysis transforms ordinal scores to the logit scale and thus to an interval-level measurement [15,16]. Furthermore, fitting data to the Rasch model allows for a detailed examination of the internal validity of the measure.

The aims of this paper are therefore twofold: (1) to provide clarity on the internal construct validity of the subscales and the total scale using factor analysis, Mokken analysis and Rasch analysis, and (2) to provide an interval conversion table if the SIPSO is found to meet the requirements of the Rasch model.

Methods

The study design and recruitment procedures have been described in detail elsewhere[7]. Briefly, SIPSO data were collected as part of two parallel surveys of younger people (aged 18-65) with non-recent stroke (at least one year ago) and living at home. The studies aimed to measure met and unmet needs. Recruitment occurred via registers maintained by national stroke centres [11] and Young Stroke groups affiliated to the Stroke Association of England and Wales[12]. People were excluded if they had a diagnosis of subarachnoid haemorrhage, had other disabling illnesses (e.g. rheumatoid arthritis or multiple sclerosis) or lived in residential care. Clinicians in charge of the stroke registers [11] and Young Stroke group coordinators [12] checked for eligibility. Eligible people were sent the SIPSO as part of the Southampton Needs Assessment Questionnaire for People with Stroke (SNAQs) and asked to return the completed forms to the researcher in Southampton. Up to two follow-up attempts were made to contact non-responders (three weeks apart).

Data Analysis

We used factor analysis, with parallel analysis to determine the significant eigenvalues [17], to examine the structure of the SIPSO and Mokken analysis to determine if the SIPSO was a valid ordinal scale [18-21]. Mokken scaling determines how likely it is that an item will be endorsed (item difficulty) and the amount of construct a person has (in this case level of integration). It assumes that a person with a certain amount of the construct (integration) will give a positive response to an item that is easier to endorse than his or her level of integration and a negative response to an item that is more difficult to endorse. It then tests this notion against the probability that the opposite will occur. Thus, Mokken scaling determines if a non-parametric probabilistic Guttman-style relationship exists in the data. Loevinger H-coefficients greater than 0.3 for individual items and the (sub) scale(s) as a whole were deemed acceptable of the probabilistic relationship.

Rasch analysis is a parametric probabilistic version of Guttman Scaling [16,22]. It is a simple logistic model, which assumes that more able people (in this case with more integration) are more likely to answer all items correctly (in this case give a more favourable response) and that easier items are more likely to be answered correctly (endorsed) by all. The interpretation of Rasch analysis has been explained in detail by others[23]. Briefly, fit to the Rasch model is acceptable when the summary chi-square interaction statistic is non-significant, showing no deviation from model expectation; where item and person summary fit statistics show a mean of zero and standard deviation of one; where individual items show non-significant chi-square fit statistics (Bonferroni adjusted), and where individual item and person residuals are within the range of +/- 2.5. Each item is examined to check that log-transformed item scores generated from the response choices reflect the increasing or decreasing latent trait to be measured. For example, a person scoring high on the subscale (good integration) should be more likely to tick the response option 4 (a positive response) than 0 (a negative response) on items which have been estimated as easy to endorse. Thresholds are the points where the probabilities of a response of either 0 or 1, and 1 or 2 (and so forth) are equally likely. If the SIPSO categories reflect increasing amount of integration, then we would expect thresholds defining the categories to be ordered along the trait accordingly. For disordered items categories can be collapsed.

In addition, the scale is expected to show invariance across key groups (e.g. gender). This requirement, also called absence of Differential Item Functioning (Dif), tests the requirement that people from different groups, with equal amounts of the underlying trait under investigation, respond to the item in the same manner; this is indicated by a non-significant ANOVA of the residuals where the key group is the main factor. Dif was examined for key groups including gender, age, centre, sample, and time since stroke.

Data should also be locally independent, in other words people's item responses should depend only on their trait level, not on their responses to other test items. This is examined with inter-item residual correlations, which should be below 0.30.

An independent t-test is used to examine if the scale is unidimensional. This tests whether any subset of items measures the same thing as another subset of items, using t-tests. If the 95% confidence interval of t-tests includes 5% unidimensionality is supported.

A reliability index, the Person Separation Index (PSI), is also calculated. The Person Separation Index (PSI) is similar to the Cronbach alpha but is derived from the linear estimates of the person's ability[22]. In a previous publication we demonstrated the reliability of the SIPSO with Cronbach's alphas of 0.93 for the Physical Integration subscale and 0.82 for the Social Integration subscale[7]. Targeting of the scale to the sample is also explored visually with person-item threshold maps.

Where data fit the model the manifest raw score from summated items can be transformed into interval scale measurement[24]. Bonferroni corrections were applied throughout the analysis to allow for multiple testing (P < 0.01)[25].

Mokken and Rasch analysis were conducted separately for the two subscales and for the SIPSO in its entirety to explore the internal construct validity of the subscales and the total SIPSO.

Factor analysis and all descriptive analyses were conducted using SPSS version 15[26]. Mokken scale analysis was undertaken with procedure 'msp' within STATA[27]. Rasch analysis was conducted using RUMM2020 software[28].

Ethics

The study was approved by the South West Multi-Centre Research Ethics Committee.

Results

In total 445 people took part (57% male, 39% female, 4% not declared). Their mean age was 53.7 (SD 9.0) and on average they had their stroke 3.5 years before we contacted them (SD 3.7, range 1-27).

Factor analysis

The SIPSO items were subjected to a Principal Component Analysis. Suitability of data for this analysis was confirmed by correlations above 0.30, a Kaiser-Meyer-Oklin value of 0.91 (above the recommended value of 0.6) and a significant Bartlett's Test of Sphericity. Two eigenvalues were greater than those produced by a Monte Carlo Parallel Analysis, together explaining 68% of the variance. This supports the originally proposed two factor structure. With a correlation of 0.56 between the two factors an Oblimin Rotation was conducted, which also supported the two-factor structure. Table 1 and 2 display the Pattern Matrix and Structure Matrix.

Table 1.

Structure Matrix SIPSO

Items Component
1 2
Item 4 .899 .529
Item 2 .889 .502
Item 1 .866 .415
Item 5 .857 .485
Item 3 .848 .660
Item 8 .539 .854
Item 7 .351 .822
Item 6 .406 .748
Item 10 .536 .683
Item 9 .434 .666
Open in a new tab

Table 2.

Pattern Matrix SIPSO

Items Component*
1 2
Item 1 .919
Item 2 .882
Item 4 .876
Item 5 .851
Item 3 .697
Item 7 .908
Item 8 .801
Item 6 .756
Item 9 .614
Item 10 .557
Open in a new tab

Mokken analysis

The Physical and Social subscales were supported by the Mokken analysis with an overall Loevinger of 0.77 for the Physical Integration subscale and 0.51 for the social integration subscale. The total scale was also subjected to Mokken analysis and we found an overall Loevinger of 0.55, which is above the accepted cut off value of 0.30. However, Mokken analysis assumes the scale is unidimensional and the data were therefore further subjected to Rasch analysis.

Rasch analysis

The Physical Integration subscale initially did not fit the Rasch model as indicated by the significant chi-square value and uniform Dif by gender for items 1 (difficulty dressing) and 5 (independence in local neighbourhood) (Table 3, analysis 1). Combining items 1 and 5 into a subtest dealt with the Dif satisfactorily and the subscale was found to fit with a non-significant chi-square, sufficient fit statistics, local independence, unidimensionality, ordered item thresholds, and item fit (analysis 2). Targeting of the subscale to the sample was good (Figure 1). We were able to produce a conversion table for the subscale (Table 4). Reliability was high with a PSI of 0.93, (similar to the Cronbach alpha of 0.93), suggesting the subscale can distinguish between 4-5 groups of people[29].

Table 3.

SIPSO Rasch analysis results

Analysis number Item fit residual Person fit residual χ2 interaction PSI Unidimensionality Independent t-test (95% CI)
Mean SD Mean SD Value (df) P
Physical Integration
1 0.145 1.271 -0.319 0.891 50.96
(30)		 0.009 0.93 2.9% (0.7 to 5.2)
2 0.033 1.544 -0.351 0.881 37.87
(24)		 0.036 0.93 1.6% (-0.6 to 3.8)
Social Integration
3 0.340 1.787 -0.329 1.059 49.70
(30)		 0.013 0.82 1.7% (-0.4 to 3.7)
4 0.188 2.824 -0.365 1.016 38.02
(24)		 0.035 0.83 2.1% (0.1 to 4.2)
5 -0.097 2.413 -0.527 0.891 8.98
(12)		 0.705 0.85 2.2% (0.1 to 4.3)
Total SIPSO
6 -0.109 3.097 -0.310 1.198 179.62
(60)		 <0.001 0.91 16.8% (14.8 to 18.9)
7 -0.261 2.801 -0.305 1.198 171.25
(60)		 <0.001 0.91 14.5% (12.4 to 16.6)
8 -0.595 3.181 -0.382 1.064 158.19
(48)		 <0.001 0.90 9.2% (7.1 to 11.3)
9 -0.328 2.619 -0.341 0.946 118.85
(36)		 <0.001 0.92 4.7% (2.5 to 6.9)
10 0.115 1.323 -0.313 0.871 58.49
(30)		 0.001 0.92 3.5% (1.3 to 5.7)
11 -0.041 1.529 -0.353 0.863 41.12
(24)		 0.016 0.92 2.7% (0.5 to 4.9)
Open in a new tab

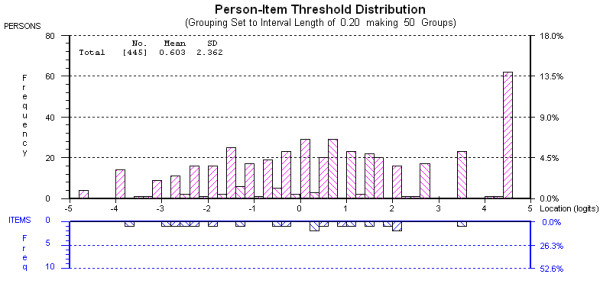
Figure 1.

Figure 1

Open in a new tab

Person Item Threshold Map Physical Integration subscale.

Table 4.

Conversion table for the Physical and Social Integration subscales

Subscale raw score (ordinal) Physical Integration Rasch log-transformed score (interval) Social Integration Rasch log-transformed score (interval)
0 0.00 0.00
1 2.05 1.79
2 3.52 3.02
3 4.55 3.89
4 5.40 4.57
5 6.18 5.17
6 6.94 5.75
7 7.65 6.30
8 8.36 6.85
9 9.05 7.46
10 9.70 8.06
11 10.37 8.72
12 11.04 9.45
13 11.73 10.24
14 12.47 11.10
15 13.22 12.05
16 14.05 13.13
17 15.01 14.33
18 16.17 15.78
19 17.77 17.61
20 20.00 20.00
Open in a new tab

The Social Integration subscale also suffered from significant uniform Dif by gender (items 7 and 10; communication and appearance in public respectively) as well as sample (item 9; visiting friends) and subsequently did not fit the Rasch model (Table 3, analysis 3). Initially we created a subtest, combining items 7 and 10 and testing these against the remaining three items but the data again did not fit as other Dif was not dealt with (analysis 4). Therefore, another subset was created combining item 9 with items 6 and 8, which visually appeared to be biased in the opposite direction (though not significantly so). This resulted in satisfactory fit to the model and unidimensionality (analysis 5). With two (super) items remaining, reliability was sufficient for individual use (PSI 0.85) and the subscale can distinguish between 3-4 groups of people [29]. Again this value was similar to the Cronbach alpha of 0.82. As above, a conversion table was produced (Table 4) and targeting was good (Figure 2).

Figure 2.

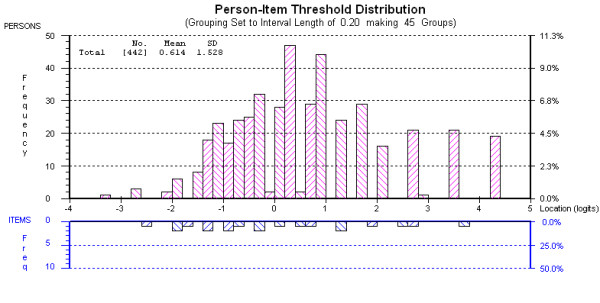
Figure 2

Open in a new tab

Person Item Threshold Map Social Integration subscale.

To test the assertion that the SIPSO makes a valid scale in its entirety all 10 SIPSO items were fitted to the Rasch model. The data deviated significantly from the Rasch model. Table 3 (analysis 6) shows a very high item fit residual standard deviation and chi-square value. Four items were disordered. Collapsing categories did not result in satisfactory fit (analysis 7); two items had high negative fit residuals (items 3 & 4), two had high positive fit residuals (items 6 & 7) and five had significant p-values (items 2, 3, 4, 6, 7). High positive fit residuals are indicators that they do not belong to the construct under investigation and should be deleted. After deletion of items 6 and 7, a further two showed significant misfit (high positive residuals, items 8 & 9, analysis 8). We deleted these two items (one at a time), at which point item 10 showed significant misfit (analysis 9) and had to be deleted. The resulting five-item subscale contained all the items belonging to the physical integration subscale and as before this showed Dif by gender (analysis 10). Creating the subtest as described above resulted in satisfactory fit to the Rasch model (analysis 11). The slightly different fit statistics between analysis 2 and 11 arises from the fact that in the latter data was rescored.

Discussion

The complementary use of factor analysis, Mokken scaling and Rasch analysis allowed us to conduct a thorough investigation of scaling properties of the SIPSO. The three analyses provided incremental evidence for the validity of the two SIPSO subscales: Factor analysis confirmed the two-factor subscale structures proposed by its originators [8]; Mokken analysis showed that the two subscales were valid ordinal scales; and Rasch analysis demonstrated that they conformed to the most stringent requirements of measurement and were unidimensional. Therefore, we are confident that the two subscales can be used.

The Mokken scaling showed an acceptable H-Loevinger Coefficient for the total SIPSO. Mokken scaling determines if an ordinal scale has been constructed but assumes that the scale is unidimensional. Unidimensionality is a requirement for summating any set of items and this is part of the basic science of measurement. Factor analysis and Rasch analysis showed that the 10 SIPSO items did not form a valid, unidimensional scale. The findings from the former found two significant eigenvalues and the latter demonstrated misfit to the Rasch model when all items were tested against the Rasch model. Rasch analysis is strict in terms of satisfying the requirement for transformation to interval scaling [30,31]. The iterative process of Rasch analysis requires unidimensionality tests to be done at each stage. Thus, factor analysis and Rasch analysis provide their own hierarchical ordering of scalability with the assumption of unidimensionality and finally the potential for interval scale transformation. Thus, the three analyses provided incremental evidence of the two subscales, but not the total SIPSO.

The Rasch model has specific properties associated with fundamental measurement, specifically, the raw score as a sufficient statistic, and the separation of person and item parameters[15]. The former is important as clinicians and others add up the set of responses to make a total score and use these to calculate change scores. As ordinal scales do not support such mathematical operations this is inappropriate. The Rasch model is the only Item Response Theory model that provides an interval scale transformation of the data. As our subscale data fit the Rasch model we were able to produce a conversion table. This table will aid clinicians and researchers in the conversion of the raw data into interval level data for the purpose of mathematical procedures such as summing subscale totals, calculating change scores and for parametric statistical analyses.

The SIPSO is relatively new and there are not many publications reporting its use even though it uniquely measures stroke specific physical and social outcome. There are no other measures that enable the evaluation of physical and social outcome in stroke although there are self-reported health related quality of life (HRQOL) scales, which include aspects of these domains. For example, frequently cited [10] stroke specific HRQOL measures include the Stroke-Specific Quality of Life Scale [32] and the Stroke Impact Scale[5]. However, these measures are much longer, contain other domains and do not have this specific focus on physical and social integration. A direct comparison between these longer HRQOL measures and the SIPSO would enable the comparison of their research and clinical utility. In addition, to compare findings in stroke populations with other groups of patients it will be useful to also include a generic measure in research.

The sample size (n = 445) for the study was estimated for the two parallel needs studies [11,12]. A retrospective sample size calculation for the Rasch analysis took into account that in order to be able to report the transformation of ordinal to interval scores normally requires a minimum of 250 cases, or 20 times the number of items, whichever is the greater. Therefore, with a ten item scale this requires 200 cases. As our sample included 445 people this was more than sufficient.

This study included only patients aged 18 to 65. Only 25% of people experience a stroke are younger than 65[2]. Therefore, our study makes no claims about the appropriateness of the SIPSO in older patients although this has been established by others [6,8,9]. The SIPSO does not include items that are only specific to people of a certain age. In addition, a key characteristic of Rasch analysis is that of specific objectivity. This is the estimation of item difficulty (or endorsability) independent of the distribution of the person estimates (in this case the amount of physical or social integration someone experiences) in the particular group of patients, and vice versa[15]. In other words, Rasch analysis is said to enable sample-free estimates of item difficulty. We can therefore conclude that the SIPSO subscales are valid and unidimensional for stroke patients, irrespective of their age.

The SIPSO was completed by post and the overall response rate in the two surveys was 53% [11,12] despite strategies that have been shown to improve response rates such as follow-up letters together with the questionnaire and the supply of self-reply envelopes [33,34]. However, this response rate tends to be in line with other postal surveys[35]. In a survey of people discharged from UK hospitals after their stroke it was shown that of those who rated their care as very poor to fair immediately following discharge, fewer responded to the follow-up survey one year later than those who had said the care was good to excellent[36]. Whether or not our surveys incurred this self-selection bias is impossible to say as we did not the opportunity to collect such data. Non-responders in our first survey were similar to responders in terms of their age and gender[11]. As for the second survey we were unable to record data on non-responders we are not able to comment on differences between responders and non-responders[12]. For future studies it would be useful to collect more data on non-responders, though the Research Governance Framework for Health and Social Care [37] and the Data Protection Act pose significant challenges in achieving such ambitions.

Conclusions

The SIPSO subscales are valid for use with stroke patients of working age but the total SIPSO is not. The conversion table can be used by clinicians and researchers to convert the raw data to interval level data after which mathematical operations (e.g. summing up subscale scores, calculating change scores) and other parametric procedures can be performed. Further work is required to explore the occurrence of bias by gender for some of the items.

Competing interests

The authors declare that they have no competing interests.

Authors' contributions

PK, AA and SG conceived of the study, were responsible for its design and coordination and helped to draft the manuscript. JL collected the data. PK performed the analyses and drafted the manuscript. All authors read and approved the final manuscript.

Pre-publication history

The pre-publication history for this paper can be accessed here:

http://www.biomedcentral.com/1471-2377/10/26/prepub

Contributor Information

Paula Kersten, Email: P.Kersten@soton.ac.uk.

Ann Ashburn, Email: Ann@soton.ac.uk.

Steve George, Email: Pluto@soton.ac.uk.

Joseph Low, Email: J.Low@medsch.ucl.ac.uk.

Acknowledgements

The authors thank the participants in this study and group co-ordinators from the Young Person's groups, without whom this study would not have been possible. This project was funded by two Stroke Association grants. The funders played no role in the design, data collection and analysis or interpretation of the data. Similarly the funders were not involved in the production of this manuscript.

References

  1. Mant J, Wade DT, Winner S. In: Health Care Needs Assessment: Stroke. Health care needs assessment: the epidemiologically based needs assessment reviews. Stevens A, Raftery J, Mant J, Simpson S, editor. Oxford: Radcliffe Medical Press; 2007. [Google Scholar]
  2. National Audit Office. Reducing Brain Damage: Faster access to better stroke care. London: National Audit Office; 2005. [Google Scholar]
  3. Department of Health. National Stroke Strategy. London. 2007.
  4. Intercollegiate Stroke Working Party. National clinical guideline for stroke. Third. London: Royal College of Physicians; 2008. [Google Scholar]
  5. Duncan PW, Wallace D, Lai SM, Johnson D, Embretson S, Laster LJ. The stroke impact scale version 2.0: Evaluation of reliability, validity, and sensitivity to change. Stroke. 1999;30:2131–40. doi: 10.1161/01.str.30.10.2131. [DOI] [PubMed] [Google Scholar]
  6. Trigg R, Wood VA, Hewer RL. Social reintegration after stroke: The first stages in the development of the subjective index of physical and social outcome (SIPSO) Clin Rehabil. 1999;13:341–53. doi: 10.1191/026921599676390259. [DOI] [PubMed] [Google Scholar]
  7. Kersten P, George S, Low J, Ashburn A, McLellan L. The subjective index of physical and social outcome: Its usefulness in a younger stroke population. Int J Rehabil Res. 2004;27:59–63. doi: 10.1097/00004356-200403000-00008. [DOI] [PubMed] [Google Scholar]
  8. Trigg R, Wood VA. The Subjective Index of Physical and Social Outcome (SIPSO): A new measure for use with stroke patients. Clin Rehabil. 2000;14:288–99. doi: 10.1191/026921500678119607. [DOI] [PubMed] [Google Scholar]
  9. Trigg R, Wood VA. The validation of the subjective index of physical and social outcome (SIPSO) Clin Rehabil. 2003;17:283–9. doi: 10.1191/0269215503cr609oa. [DOI] [PubMed] [Google Scholar]
  10. Geyh S, Cieza A, Kollerits B, Grimby G, Stucki G. Content comparison of health-related quality of life measures used in stroke based on the international classification of functioning, disability and health (ICF): A systematic review. Qual Life Res. 2007;16:833–51. doi: 10.1007/s11136-007-9174-8. [DOI] [PubMed] [Google Scholar]
  11. Kersten P, Low JTS, Ashburn A, George SL, McLellan DL. The unmet needs of young people who have had a stroke: Results of a national UK survey. Disabil Rehabil. 2002;24:860–6. doi: 10.1080/09638280210142167. [DOI] [PubMed] [Google Scholar]
  12. Low JTS, Kersten P, Ashburn A, George S, McLellan DL. A study to evaluate the met and unmet needs of members belonging to young stroke groups affiliated with the stroke association. Disabil Rehabil. 2003;25:1052–6. doi: 10.1080/0963828031000069753. [DOI] [PubMed] [Google Scholar]
  13. Harrington R, Taylor G, Hollinghurst S, Reed M, Kay H, Wood VA. A community-based exercise and education scheme for stroke survivors: a randomized controlled trial and economic evaluation. Clin Rehabil. 2010;24:3–15. doi: 10.1177/0269215509347437. [DOI] [PubMed] [Google Scholar]
  14. Lord S, McPherson KM, McNaughton HK, Rochester L, Weatherall M. How feasible is the attainment of community ambulation after stroke? A pilot randomized controlled trial to evaluate community-based physiotherapy in subacute stroke. Clin Rehabil. 2008;22:215–25. doi: 10.1177/0269215507081922. [DOI] [PubMed] [Google Scholar]
  15. Bond TG, Fox CM. Applying the Rasch model. Fundamental measurement in the human sciences. London: Lawrence Erlbaum Associates; 2001. pp. 144–6. [Google Scholar]
  16. Rasch G. Probabilistic models for some intelligence and attainment tests. Copenhagen: Danish Institution for Educational Research; 1960. [Google Scholar]
  17. Horn JL. A rationale and test for the number of factors in factor analysis. Psychometrica. 1965;30:179–85. doi: 10.1007/BF02289447. [DOI] [PubMed] [Google Scholar]
  18. Mokken RJ. The theory and procedure of scale analysis with applications in political research. New York, Berlin: Walter de Gruyter, Mouton; 1971. [Google Scholar]
  19. Mokken RJ, Lewis C. A nonparametric approach to the analysis of dichotomous item responses. Appl Psychol Meas. 1982;6:417–30. doi: 10.1177/014662168200600404. [DOI] [Google Scholar]
  20. Molenaar IW. A weighted Loevinger H-coefficient extending Mokken scaling to multicategory items. Kwantitatieve Methoden. 1988;9:115–26. [Google Scholar]
  21. van Shuur WH. Mokken scale analysis: Between the Guttman scale and parametric Item response theory. Political Analysis. 2003;11:139–63. doi: 10.1093/pan/mpg002. [DOI] [Google Scholar]
  22. Andrich D. Rasch models for measurement series: quantitative applications in the social sciences no. 68. London: Sage Publications; 1988. [Google Scholar]
  23. Tennant A, Conaghan PG. The Rasch measurement model in rheumatology: What is it and why use it? When should it be applied, and what should one look for in a Rasch paper? Arthritis Care Res. 2007;57:1358–62. doi: 10.1002/art.23108. [DOI] [PubMed] [Google Scholar]
  24. Wright BD, Stone MH. Best test design. Chicago: Mesa press; 1979. [Google Scholar]
  25. Bland JM, Altman DG. Multiple significance tests: the Bonferroni method. BMJ. 1995;310:170. doi: 10.1136/bmj.310.6973.170. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. SPSS Inc. SPSS 15.0 for Windows. Release 15.0.1. 2007.
  27. StataCorp. Stata Statistical Software: Release 10. College Station, TX: StataCorp LP; 2007. [Google Scholar]
  28. Andrich D, lyne A, Sheridan B, Luo G. RUMM 2020. Perth: RUMM Laboratory; 2003. [Google Scholar]
  29. Fisher WJr. Reliability Statistics. Rasch Measurement Transactions. 1992;6:238. [Google Scholar]
  30. Perline R, Wright BD, Wainer H. The Rasch model as additive conjoint measurement. Appl Psychol Meas. 1979;3:237–56. doi: 10.1177/014662167900300213. [DOI] [Google Scholar]
  31. Rasch G. Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability. IV. Berkeley: University of Chicago Press; 1980. On general laws and the meaning of measurement in psychology; pp. 321–34. [Google Scholar]
  32. Williams LS, Weinberger M, Harris LE, Clark DO, Biller J. Development of a stroke-specific quality of life scale. Stroke. 1999;30:1362–9. doi: 10.1161/01.str.30.7.1362. [DOI] [PubMed] [Google Scholar]
  33. Edwards P, Roberts I, Clarke M, Di Guiseppi C, Pratap S, Wentz R. Increasing response rates to postal questionnaires: systematic review. BMJ. 2002;324:1183–5. doi: 10.1136/bmj.324.7347.1183. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Oppenheim AN. Questionnaire design, interviewing and attitude measurement. 2. London: Continuum; 1992. [Google Scholar]
  35. Bowling A. Investigating health and health services. Buckingham: Open University Press; 1997. Research methods in health. [Google Scholar]
  36. Healthcare Commission. Survey of patients 2006. Caring for people after they have had a stroke. A follow-up survey of patients. Commission for Healthcare Audit and Inspection. 2006.
  37. Department of Health. Research Governance Framework for Health and Social Care. 2. London, Department of Health; 2005. [Google Scholar]

Articles from BMC Neurology are provided here courtesy of BMC

RESOURCES