Skip to main content
. Author manuscript; available in PMC: 2010 May 24.
Published in final edited form as: Antivir Ther. 2009;14(3):459–464.

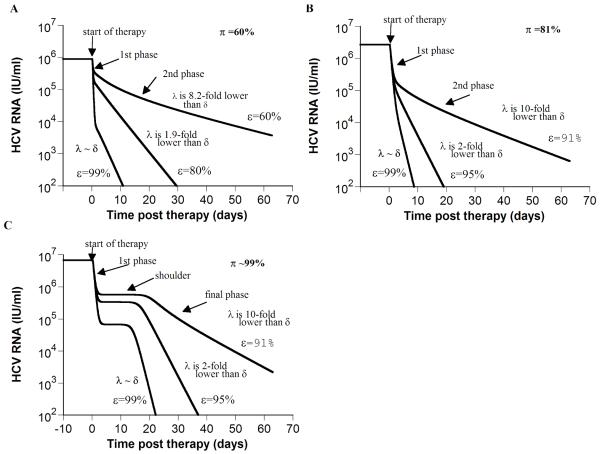
Figure 1. Model predictions of HCV RNA kinetics during successful treatment (ε >εc).

Figure 1

If the total drug efficacy, ε, is higher than the critical drug efficacy, εc, our model, which includes hepatocyte proliferation [5], predicts two HCV RNA kinetic patterns: biphasic (A and B) and triphasic (C). Using Eq. 3 and parameter values of each in-silico patient, we calculated the theoretical final viral decay slope, λ. In addition, we directly measured from the final phase the viral decline slope (λestimated) via linear regression of the kinetic data. When ε is low (i.e., 60% in (A) or 91% in (B and C)), λ ranged from 10-fold to 8-fold lower than δ, and λestimated = 0.06, 0.08 and 0.12 day−1, respectively. Whereas when ε =99% λ is close to δ, and λestimated = 0.46, 0.85 and 0.84 day−1 in A, B and C, respectively. Note the strong dependence of the final phase slope, λestimated, on effectiveness, ε,. e.g., in (B) λestimated increases from 0.08 day−1 to 0.85 day−1as ε increases from 91% to 99%. The calculated baseline percentage of hepatocytes that are HCV-infected, π (see Online Supplementary material), is 12%, 90% and 99% in (A), (B) and (C), respectively. Parameter values in (A) are Tmax = 7.3 × 106 cells ml−1; dT = 3.5 × 10−3 day−1; δ = 0.47 day−1; β = 5.7 × 10−7 ml virions−1 day−1; c = 6.0 day−1; p = 1.5 virions cell−1 day−1; rT = 3.0 day−1; rI = 0.7 day−1; s = 1 cell day−1 ml−1;εc = 55%. With these parameter values T0 =7.3 × 106 cells ml−1, T̄ =2.4 × 106 cells ml−1, Ī =3.6 × 106 cells ml−1, V̄ =5.95 log10 IU/ml. For both (B) and (C), Tmax = 9.8 × 106 cells ml−1; dT = 1.34 × 10−2 day−1; δ = 1.0 day−1; β = 8.3 × 10−7 ml virions−1 day−1; c = 2.4 day−1; p = 2.9 virions cell−1 day−1; rT = 3.0 day−1; s = 1 cell day−1 ml−1; εc = 89.9%, T0 =9.8 × 106 cells ml−1. As previously explained [5], if we increase the infected cell replication rate – here from rI = 0.7 day−1 (used in (B)) to rI = 2.3 day−1 - a shoulder phase emerges in (C). In (B) and (C), T̄ =4.9 × 105 and 0.23 cells ml−1, Ī = 2.2 × 106 and 5.6 × 106 cells ml−1, V̄ = 6.4 and 6.8 log10 IU/ml, respectively.