Mechanisms for the Intracellular Manipulation of Organelles by Conventional Electroporation

Abstract

Conventional electroporation (EP) changes both the conductance and molecular permeability of the plasma membrane (PM) of cells and is a standard method for delivering both biologically active and probe molecules of a wide range of sizes into cells. However, the underlying mechanisms at the molecular and cellular levels remain controversial. Here we introduce a mathematical cell model that contains representative organelles (nucleus, endoplasmic reticulum, mitochondria) and includes a dynamic EP model, which describes formation, expansion, contraction, and destruction for the plasma and all organelle membranes. We show that conventional EP provides transient electrical pathways into the cell, sufficient to create significant intracellular fields. This emerging intracellular electrical field is a secondary effect due to EP and can cause transmembrane voltages at the organelles, which are large enough and long enough to gate organelle channels, and even sufficient, at some field strengths, for the poration of organelle membranes. This suggests an alternative to nanosecond pulsed electric fields for intracellular manipulations.

Introduction

The cell interior contains complex electric signaling circuits and intracellular bioelectric interactions that are important for regeneration, morphogenesis, and left-right patterning (1). Embryonic development, for example, is controlled by electrophoretic morphogen gradients within multicellular arrays, and perturbations cause randomization of gene expression (2). Cell organelles themselves are also capable of generating and conveying electric signals (3). Mitochondria are prominent examples, as their dysfunction underlies many diseases (4).

The manipulation of cellular organelles by external electric fields is therefore of significant interest and has recently received much attention by the application of megavolt-per-meter (10⁶–10⁷ V/m), nanosecond-pulsed electric fields (nsPEF), for which a more sophisticated pulse generation technology is required (5–13). Supra-EP then occurs in all of the cell's membranes (14,15). Pores remain small, however—able to transport only small ions and molecules, but not significant amounts of conventional EP markers. Molecular dynamics (MD) simulations of very small, finite-size membrane patches for these extremely large field strengths provide detailed molecular information about the complex dipolar interplay of lipids, water, and ions during EP (16,17). MD simulations confirm the formation of pores and validate the main features of earlier ideas about pore geometries and dipole reorientations. MD also demonstrates the translocation of charged lipids via a pore (18,19).

The plasma membrane (PM) of cells is a frequency-dependent amplifier of the applied electromagnetic field E_app(f) and becomes electrically transparent at frequencies f > ∼100 kHz (20). This can be understood from the PM gain G_PM(f) = E_PM(f)/E_app(f), which is G_PM ∝ 3r_cell/2d_PM ≥ 10³ at low frequencies, but rapidly decreases for f ≥ 100 kHz (20). Accordingly, it has been argued that nsPEFs with frequency components f ≥ 100 kHz provide a unique way to extend the reach of an applied electric field to intracellular structures, e.g., by altering the nuclear or mitochondrial transmembrane voltage (5–7). Here we argue that nsPEFs may not be required. Instead we submit that much longer pulses (with frequency components f < 100 kHz), which have conventionally been used for the electroporation (EP) of the PM, can also cause nonthermal intracellular effects, including organelle EP.

Conventional EP pulses are defined to involve characteristic times (pulse duration and rise and fall times) that are longer than the PM charging time τ_PM—typically 0.1–1 μs for mammalian cells in suspension. If passive mathematical models are applied to membranes under conventional EP conditions, as above for G_PM and shown back in 1959 by Pauly and Schwan (21), then the cell interior is essentially shielded from the external electric field after displacement currents decay. This occurs because small electrolyte ions have sufficient time to charge the PM for exposure times exceeding τ_PM and thus to completely polarize the PM (21). The nsPEFs, then, are defined by characteristic times shorter than τ_PM—i.e., too short to shield the cell interior by charging of the PM.

However, the above amplification and charging time concepts apply only as long as there is no EP at the PM. Passive conductive and dielectric mathematical models (22) neglect membrane alterations, which must occur during EP to deliver molecules into cells (23,24). This is fundamental to gene therapy by DNA transfection (25–27), electro-chemotherapy (28), delivery of plasmid DNA to treat solid tumors (29–32), transport of drugs through tissue barriers such as skin (33), high-throughput siRNA delivery and screening of gene-specific silencing by RNA interference (34), and solid tumor treatment without drugs (35–37).

The creation of transient aqueous pores is generally regarded as a robust and universal mechanism by which cells, depending on their size, respond to conventional EP pulses of magnitudes larger than ∼10⁴ V/m and thus provide transient electrical pathways into the cell (38). Therefore, the cell interior is not shielded from the extracellular electric field under EP conditions and the electric field penetrates into the cell through pores (39,40).

Can we then expect organelle EP due to conventional pulses? Due to the size-dependence of G_organelle ∝ 3r_organelle/2d_organelle, the smaller organelles require a somewhat larger field strength than the PM to reach a sufficient transmembrane potential for EP. This larger field strength may be estimated from the factor r_PM/r_organelle, which is 10:3 for typical values of the PM and the nucleus, but depends eventually on the actual value of intracellular electric field. The quantification of this intracellular electric field emerging due to conventional EP and the likely consequences is a central object of this article. In particular, we demonstrate that conventional EP can lead to significant internal electric fields, sufficient to gate ubiquitous voltage-dependent organelle channels and to cause organelle EP.

Methods

System model for a cell with organelles, multiscale transport lattices, and dynamic EP model

We use a multiscale transport lattice (TL) (14,15,20,41,42) to represent increasingly realistic cell models. Our present cell system model includes relevant organelles (nucleus, endoplasmic reticulum, mitochondria) and a dynamic EP model at the membrane level. Dynamic pore size behavior in tissue models under conditions of irreversible EP and supra-EP has been described with this approach (36,37). This article and a recent article by Krassowska and Filev (43) are, to our knowledge, the first EP studies of isolated cells to describe dynamic pore size changes by a mathematical model. Our results provide new insights into electric conditions at both the PM and inside a cell, from which we infer a mechanistic basis for direct intracellular electric effects. The system model for a cell with organelles and its implementation through modular, multiscale TL is detailed in the Supporting Material. Specific emphasis is given to the integration of the dynamic EP model into the TL method.

Pulse waveforms

Exponential pulses E_app(t) = $E_{\text{app}}^0$ exp [−t/τ_pulse] with time constant τ_pulse are widely used conventional EP waveforms and are easy to generate. The applied field for parallel plane electrodes with spacing L is $E_{\text{app}}^0$ = V_app⁰/L, with the applied voltage V_app⁰. For an illustrative case, we focus on pulses with τ_pulse = 40 μs, which were reported to induce apoptosis in Jurkat T-lymphoblasts and HL-60 cells (44), and assume a pulse rise time of 1 μs. The robustness of the EP mechanism suggests that our conclusions are also valid for other waveforms, as shown in the Supporting Material for the case of a trapezoidal pulse with duration of 100 μs, and pulse rise and fall times of 1 μs.

Results

Dynamic and asymmetric EP

The PM transmembrane voltage Δψ_PM(t) plays a central role in interaction mechanisms that stimulate and modify cells by physiologic electric fields (45) and is dominant for EP at larger fields (38). Fig. 1 A shows Δψ_PM(t) at the cathodic and anodic poles of the cell model for the exponential pulse (E_app⁰ = 1 kV/cm, τ_pulse = 40 μs, rise time 1 μs) on a logarithmic timescale. Initially Δψ_PM(t) starts off at the PM resting potential of –90 mV. Note that Δψ_{PM, anode}(t) at the anodic side is displayed here, for display purposes, as –Δψ_{PM, anode}(t) for a better comparison of the temporal behavior and respective magnitudes at both sides. Therefore, Δψ_{PM, anode}(t) starts off at +90 mV in Fig. 1 A.

Figure 1.

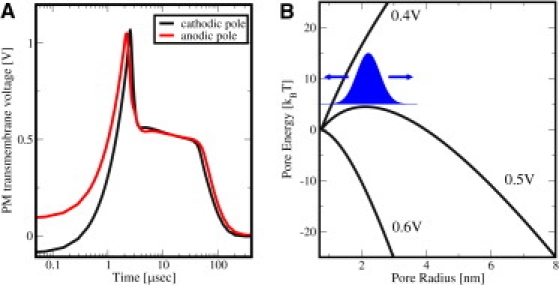
(A) PM transmembrane voltage for the exponential pulse (E⁰_app = 1 kV/cm, τ_pulse = 40 μs) anodic and cathodic poles of the cell model. Δψ_{PM, anode} is displayed here as –Δψ_{PM, anode} for better comparison with the behavior of the cathodic pole. Starting at the resting potential, both Δψ_PM rise to their respective peaks, followed by a drop and a voltage-regulated plateau value of ∼0.5 V. Notably, Δψ_PM does not follow the time-dependence of the exponential pulse. After the pulse Δψ_PM remains at approximately zero voltage (depolarized PM) for the lifetime of the pores. (B) Pore energy W (relative to the minimum pore size energy W(r_{p, min} = 0.8 nm), see Supporting Material) as function of pore radius for three transmembrane potentials. For Δψ_PM = 0.5 V, the plateau value typical for conventional EP, an energy maximum at pore radius of 2.1 nm causes the part of the pore distribution (sketched by blue profile) with pore sizes smaller than 2.1 nm to shift to smaller pore sizes, and simultaneously the other part with pore sizes larger than 2.1 nm to shift to larger pore sizes. In contrast, lower (e.g., 0.4 V) and larger (e.g., 0.6 V) values of Δψ_PM lead exclusively to either pore shrinkage or pore expansion, respectively. As the postpulse transmembrane voltage is essentially zero for EP, all pores eventually shrink to minimum size in this model (reversible EP).

After the initial rise of Δψ_PM due to membrane charging, Δψ_PM at the anodic pole reaches a peak. Membrane charging cannot continue at this peak, as the formation of pores in the PM leads to a high-conductance of the membrane and partly discharges the membrane. The peak is followed by a sudden drop of Δψ_{PM, anode}(t) associated with pore expansion. The cathodic pole follows in time, whereby the Δψ_PM peak value is ∼5% larger on the cathodic side. After the voltage drop, a voltage-regulated plateau occurs at ∼0.5 V. At the end of the plateau, Δψ_PM(t) decays exponentially on both poles and follows the time-dependence of the external pulse, but does not immediately return to the resting potential. Instead, the many pores discharge the PM with a slow recovery, while minimum size pores vanish with a mean lifetime of 3 ms (46). Hence, Δψ_PM is essentially zero after the pulse. Overall Δψ_PM values at the anodic and cathodic poles are only slightly different.

The spatially distributed electric response of the cell system model to this exponential pulse (E_app⁰ = 1 kV/cm, τ_pulse = 40 μs, rise time 1 μs) is given in Fig. 2. Equipotential lines (black) in the left panels (A–D) show the dynamic redistribution of the electric field around the cell and, due to EP at the PM, also partially penetrating into the cell interior. White dots at the PM indicate local membrane areas with at least 50 pores. This corresponds to a pore density of N_p = 10¹³ m⁻², based on local discretized membrane areas of l × d_sys = 4.7 μm². Pore size histograms in the right panels of Fig. 2 give the total number of pores on the anodic and cathodic PM sides with a particular pore radius range, using a bin size of 0.1 nm.

Figure 2.

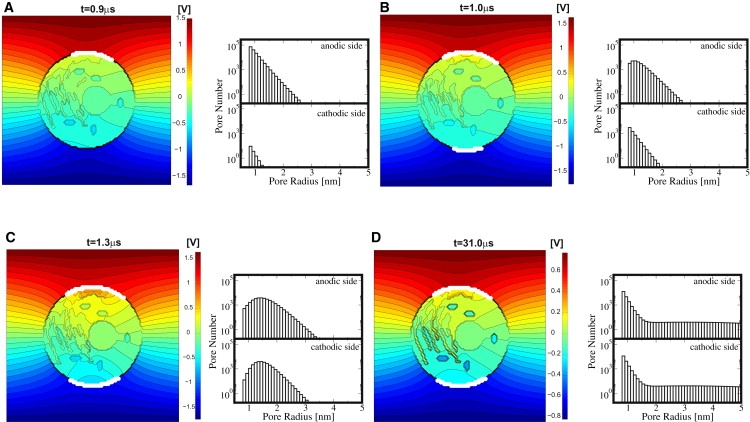
(Left panels) Distributed electrical response of the cell model to exponential pulse (E⁰_app = 1 kV/cm, τ_pulse = 40 μs, 1 μs rise time); color bar shows the potential scale. White dots are local membrane sites with ≥50 pores (corresponding to a pore density of N_p = 10¹³m⁻²). (Right panels) Pore histograms for the anodic and cathodic membrane side give the total number of pores and their size within intervals of 0.1 nm. (A) EP starts at t = 0.9 μs on the anodic side, followed at t = 1.0 μs on the cathodic side in panel B. Pore expansion also starts initially at the anodic side. (C) Significant pore expansion at t = 1.3 μs at both the anodic and cathodic side; the presence of intracellular equipotential lines reveal the emergence of electric fields in the cell interior. (D) At t = 31 μs, the pore histograms regain maxima at r_{p, min}, but simultaneously show nonequilibrium tails toward larger pores. Pore histograms are similar on both cell sides, anodic and cathodic side mean pore sizes, and pore number differ only slightly (see text). Note that the organelles do not show intraorganelle electric fields, as there is no organelle EP here.

EP at the PM is strikingly dynamic and asymmetric. At early times, a significant asymmetry appears in the EP spatial distribution and also in the associated pore histograms (Fig. 2 A). This asymmetry is caused by the PM's resting potential source. Specifically the anodic side is hyperpolarized by the applied pulse and pores are created there first at t = 0.9 μs (during the pulse rise time). EP of the cathodic side follows at t = 1 μs, as shown in Fig. 2 B. Pore expansion at the anodic side has then already started. The lateral extent of the electroporated region on each cell side increases with time on both sides. This agrees with the important result in Krassowska and Filev (43) that EP sets in at different times at the anodic and cathodic sides. There is a difference of 0.1 μs here, but this time delay decreases with increasing field strength because of faster PM charging (not shown).

At t = 1.3 μs, shown in Fig. 2 C, pore expansion has occurred at both PM sides. These expanding pores are available for uptake and release of larger molecules. Pore expansion after the transmembrane potential peak, as discussed in Fig. S1 and in the Supporting Material, leads to a further reduction in Δψ_PM. Because the pore formation term (Eq. S2 in the Supporting Material) in our model depends exponentially on the local Δψ_PM value squared, the creation of new pores is then greatly reduced. Thus, after EP onset, pore creation is reduced and pore expansion becomes important.

The contribution of the electric pore energy, W_el (see Supporting Material), to the total pore energy, W, decreases for lower values of Δψ_PM. Fig. 1 B shows that, while all pores expand for Δψ_PM = 0.6 V, those pores shrink again as soon as Δψ_PM reaches values of 0.4 V and below. A particular case (indicated by the blue profile in Fig. 1 B) occurs at Δψ_PM = 0.5 V, where pore expansion is expected for pores larger than a 2-nm radius while pore shrinkage is expected for pores smaller than ∼2 nm in radius. Incidentally, Δψ_PM reaches a plateau with values of ∼0.5 V during the pulse, as discussed above and shown in Fig. 1 A.

Hence, pore shrinkage occurs for most pores even during the pulse, as shown in Fig. 2 D. Therefore, not all pores increase in size with pulse duration. In fact, our in silico results suggest that most pores do not expand and instead remain at a size below 2 nm. Only some pores from the entire pore distribution, that is, those which have reached a 2-nm radius before the Δψ_PM plateau, expand to significantly larger sizes. In other words, a subpopulation of larger pores emerges during the Δψ_PM-plateau. Thus, the pore histograms in Fig. 2 D show a maximum at the minimum pores size (r_p, min = 0.8 nm), but retain long tails extending to large pore radii > 2 nm. After the pulse, as membrane discharge has Δψ_PM→ 0, all pores eventually shrink to a minimum-size and decay (reversible EP).

A somewhat larger lateral PM region is electroporated on the anodic side, but not symmetric in polar angle (the angle between the electric field direction and membrane site). This occurs due to the presence of organelles that are purposefully unevenly distributed within the cell model. Organelles distort the intracellular electric field and contribute further to EP asymmetries at the PM. To our knowledge, this effect has not been previously noted.

The largest local pore densities occur in both polar regions because they experience the largest Δψ_PM-peak values. However, the largest pores are found at the boundary of the electroporated-to-nonelectroporated region, as shown by Krassowska and Filev (43). Importantly, the Δψ_PM at the pole and most of the electroporated region (white dots in Fig. 2) has essentially the same Δψ_PM-plateau value (≈0.5 V). Only at the border to the nonelectroporated region is Δψ_PM larger (≈0.6 V).

As explained through Fig. 1 B, larger Δψ_PM-values give rise to a larger pore-expanding force, even for pores that are still small. The pore size distribution along the PM is thus not uniform, and also the membrane conductance is spatially dependent. EP models thus disagree with phenomenological electropermeabilization descriptions that assign a uniform permeability to a perturbed membrane region. All these findings agree qualitatively with the results by Krassowska and Filev (43), even though their EP model is slightly different. This suggests robustness of the underlying biophysical mechanisms.

Because of the cell's resting potential, the total number of PM pores created on the anodic side is ∼18% smaller than the cathodic side. Note that we use here the conductivity of physiologic saline (σ = 1.2 S/m) for both extra- and intracellular electrolytes. However, even with this difference, the mean pore radius 〈r_p〉 on both sides remains similar (anode 〈r_p〉 = 1.84 nm, cathode 〈r_p〉 = 1.78 nm). Remarkably, this finding depends on the ionic strengths of the electrolytes, and may be even reversed if the extracellular conductivity σ_ex of the medium exceeds the intracellular conductivity σ_in. In agreement with the results of Krassowska and Filev (43), for example, a choice of σ_ex = 5 S/m and σ_in = 0.4 S/m leads to 16% more pores on the anodic side, even with the resting potential present.

Note that reported volume-averaged intracellular conductivities are three-to-five times smaller than the extracellular value for physiologic saline, and are due to the crowded environment that excludes electrolyte volume. The presence of organelles is tantamount to having a smaller effective intracellular conductivity, as can be shown from the behavior of pore number reversal, but the inclusion of many more organelles to represent a truly crowded cell interior is not yet computationally feasible.

Asymmetric features of EP are well known. They have been observed in the transport of molecules and dyes, with entry predominantly through either the anodic or cathodic cell hemispheres for monopolar pulses (48–55). This asymmetric transport has been also associated with primary electric asymmetries in the transmembrane voltage Δψ_PM, the membrane conductance G_PM (11,49), and also with the pore distributions n_p itself (53), leading to asymmetric current-voltage (I-V) behavior. Intriguingly, synthetic nanopores also exhibit an asymmetric current-voltage behavior (56), but this is attributed to the intrinsic pore geometry, which is asymmetric. An asymmetric shape is not generally expected for pores due to EP, and to date has not been a notable MD finding.

To date, four major contributions to asymmetric EP have been proposed: 1), electrolyte ionic strength of the solution and ionic differences between the cell interior and exterior; 2), the cell's resting potential; 3), phospholipid asymmetry (54,56); and 4), an intrinsic membrane property such as the membrane dipole potential (57,58). As shown here, properties 1–3 can contribute to EP asymmetry, but the differences in Δψ_PM, G_PM, and n_p between the anodic and cathodic sides are rather small. As discussed above, they appear insufficient to explain the observed effects. Also note that asymmetric transport can occur even for small ions such as Ca²⁺ under experimental conditions in which the inner and outer membrane leaflets have identical composition and a resting potential is zero (58). While the dynamic EP pattern at the PM thus shows considerable complex detail (43), we now focus here on intracellular fields and interactions that are the consequence of EP at the PM.

Intracellular electric fields emerging from conventional EP

As indicated in Fig. 2 by the presence of black equipotential lines inside the cell, intracellular electric fields E_int appear because of EP of the PM. This leads to a partial redistribution of the external electric field and therefore an electric current through the cell. As such, the intracellular electric field, E_int, emerges as an intrinsic consequence and thus a secondary effect of EP. As shown in the left panels of Fig. 2, E_int is heterogeneous and changes over time: E_int emerges with the onset of EP at t = 0.9 μs, increases during the pulse due to pore expansion, and eventually decays.

E_int also varies spatially within the cell. For simplicity and illustration, Fig. 3 A shows E_int at the center of the cell without any organelles present as function of time for the exponential pulse ($E_{\text{app}}^0$ = 1 kV/cm, τ_pulse = 40 μs, 1 μs rise time) for an active and a passive PM. For a passive PM (EP turned off), the pulse results in insignificant values of E_int arising only from membrane displacement currents. These are largest during the pulse rise time, and decay afterwards.

Figure 3.

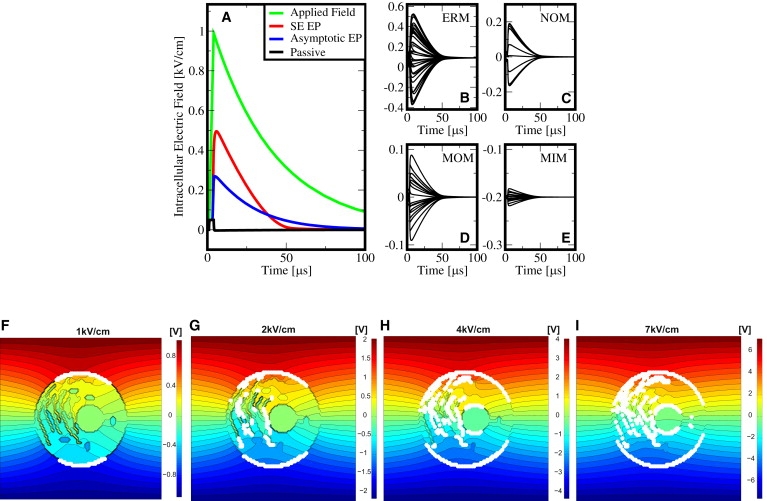
Intracellular electric fields in response to the exponential pulse of Fig. 2. (A) The intracellular field E_int, at the cell center without any organelle present: a passive PM yields essentially zero E_int except during the brief pulse rise time (black). The asymptotic EP model without pore expansion leads to E_int values of ∼25% of E_app (blue). The SE EP model (based on Eq. S1 and Eq. S2 in the Supporting Material) leads to ∼50% of the applied field due to pore expansion and therefore further membrane conductance increase (red). (B–E) Local organelle transmembrane voltages change at the ERM, NOM, MIM, and MOM from their respective resting potentials by several tens of millivolts, whereby a larger size of the organelle leads to a larger change in the organelle transmembrane voltage. These deviations from organelle resting potentials (hyper- and depolarized) provide the possibility of stimulating voltage-dependent organelle channels. (F–I) Distributed electric response of the cell system model to the exponential pulse of Fig. 2 (τ_pulse = 40 μs) but for different field strengths at a time point of t = 20 μs. EP is highlighted by white dots that correspond to local sites with at least 50 pores (corresponding to a pore density of N_p = 10¹³ m⁻²). With increasing field strength, the distance of the intracellular equipotential lines decreases compared to the distance of the extracellular potentials, demonstrating increased values of the intracellular electric fields. Organelle EP emerges at larger field strengths, in particular for 2 kV/cm at the ERM (G), for 4 kV/cm at the NOM and NIM (H), and for at 7 kV/cm at the MOM (I). The boundary between the electroporated and nonelectroporated region along the PM circumference also depends on the field strength and expands toward the equatorial region for larger field strengths (also seen for the NOM) (41). Compare the progressively increased organelle EP shown here to the smaller magnitude conventional EP pulse of Fig. 2, for which there is no intracellular EP.

The active membrane response (EP turned on) is strikingly different. The asymptotic EP model (59) yields a partial redistribution of the external electric field through the cell interior because of minimum-sized pores (r_p, min = 0.8 nm) in the PM and therefore E_int reaches ∼25% of $E_{\text{app}}^0$. Moreover, EP based on the Smoluchowski equation (SE, see Supporting Material), which includes the expansion of pores to larger than minimum sizes, leads to an internal electric field E_int of almost 50% of E_app⁰. Even larger values of E_int thus result from the nonlinear increase of pore conductance G_m due to pore expansion. In other words, the larger the pores the larger the resulting intracellular electric field. In contrast to reports that nsPEFs are necessary to achieve intracellular manipulation (5–13), electric pulses with duration longer than τ_PM, as shown here, can also achieve significant intracellular electric fields E_int.

Why are these values of E_int significant?

First, they can cause transient electric perturbations of all organelle transmembrane voltages, potentially affecting membrane processes in organelles and thus leading to a response by voltage-sensitive organelle channels and pumps. Fig. 3, B–E, shows, for example, transient changes of organelle transmembrane voltages due to the exponential pulse (E_app⁰ = 1 kV/cm, τ_pulse = 40 μs, rise time 1 μs) presented in Fig. 2. Notably, the membranes of the larger extended organelles—endoplasmic reticulum (ERM), inner (NIM), and outer (NOM) membrane of the nucleus—experience the largest perturbation of their transmembrane voltages (up to 500 mV), whereas the smaller extended mitochondria experience a smaller perturbation of their inner membrane (MIM) and outer membrane (MOM) transmembrane voltages (up to 100 mV). These changes in transmembrane voltage values are sufficient in magnitude to activate membrane channels and pumps (45).

As a consequence, voltage-dependent Ca²⁺ channels in the ERM that are known to participate in the control of cytoplasmic Ca²⁺ concentration (60,61) may be affected. These channels regulate cell processes such as secretion and gene transcription and have also been identified as a second-messenger signal for the induction of either apoptosis or necrosis (62). Thus, changes in the intracellular Ca²⁺ concentrations may be expected for conventional EP pulses, driven by the release of intracellular stores.

Intraorganelle pH values are regulated by many organelles to suit their individual biochemical functions (63), and transient changes can be caused by the electric perturbation of V-ATPase proton pumps. Furthermore, the mitochondrial permeability transition pore reacts to changes in the transmembrane voltage of the MIM and, if sufficiently depolarized, may inhibit oxidative phosphorylation and the stimulation of ATP hydrolysis (64,65). These are three examples of unexplored possibilities that may exist for causing intracellular effects by changing organelle transmembrane voltages through conventional EP.

Channel activation, however, also requires time, typically on the millisecond timescale (45). But the described mechanism for generating significant intracellular electric fields via EP of the PM holds true also for longer (and shorter) than the above 40-μs exponential pulses. For example, Fig. 4 B shows transmembrane voltage changes at various local sites at the ERM, which result from a 2-ms trapezoidal pulse with $E_{\text{app}}^0$ = 0.7 kV/cm, demonstrating sufficient values of Δψ_ERM for membrane channel activation (45). This response may be considered as nonthermal, as an associated increase due to Joule heating is estimated to be <3°C.

Figure 4.

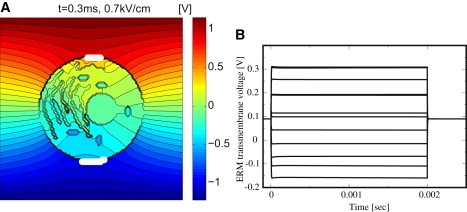
(A) Distributed electrical response to a 2 ms trapezoidal pulse with E⁰_app = 0.7 kV/cm at t = 0.3 ms (long after the high conductance state is achieved at the PM). EP occurs in a smaller PM region than compared to Figs. 1 and 2 due to the smaller field strength E⁰, but still sufficient to yield significant intracellular electric fields E_int, as shown by the presence of equipotential lines inside the cell. (B) Transients of resulting transmembrane voltages changes, Δψ_ERM(t), at various local sites of the ERM in panel A. Δψ_ERM(t) starts off at the ERM resting potential of 0.09 V and returns to this value postpulse. During the pulse, significant values of Δψ_ERM(t) in duration and magnitude for channel activation are shown.

Second, as EP of the PM leads to significant E_int, pulse parameters may be specified that lead to organelle EP. Experimental indications for intracellular EP by conventional pulses based on fluorescein-transfer into organelles have been reported with microelectrodes that are positioned close to individual cells, and which create spatially focused inhomogeneous electric fields (23). Isolated organelles such as mitochondria are known to be electroporatable, but their smaller size requires applied field strengths (66) that are larger than typically used for mammalian cell EP. Indeed, organelle EP by conventional field pulses emerges in our model at larger electric field amplitudes, as shown in Fig. 3 (F–I). EP of the ERM is shown at 2 kV/cm, followed by EP at the NM at 4 kV/cm, and EP at the MOM at 7 kV/cm.

Each larger field strength thus opens new pathways for molecular, ionic, and potentially genetic transport between the cytoplasm and different intracellular compartments (organelles). For example, EP of the nucleus provides a direct path for nucleo-cytoplasmic exchange of genetic material in parallel to nuclear pore complexes, and is relevant for optimized nucleofection protocols (67–69). In addition, the organelle membranes, if sufficiently electroporated, become depolarized after the pulse for the duration of the average pore lifetime. Depolarization of the MIM has relevance in cell death by apoptosis (64,65).

Applied electric fields within biological systems inescapably generate some Joule heating even if the predominant interaction mechanism (e.g., voltage-gated channels, conventional EP for widely employed conditions) is nonthermal. The possibility of effects due to intracellular electric fields from unusually large magnitude conventional EP fields considered here also falls into this category. This can be understood by noting that for organelle EP predicted here the largest electric field pulse (7 kV/cm; τ_pulse = 40 μs) results in an expected worst case (adiabatic) temperature rise of ∼3°C. Even for a human-core-body temperature of 37°C, the maximum temperature is ∼40°C. Initial temperatures in the extremities and for in vitro experiments are smaller, so that maximum values are also smaller. Our overall conclusion is therefore that the emerging intracellular electric fields described here can result in organelle interactions, which are essentially nonthermal in nature.

Discussion

As argued here, complex and increasingly realistic cell models can predict the extent of EP in membranes throughout a cell. We have shown that conventional EP leads to pores in the PM that may expand to several nanometers in radius, in general agreement with Krassowska and Filev (43). The postpeak transmembrane voltage during the pulse is ∼0.5 V, leading to the simultaneous presence of both small and larger pores. Further, intracellular electric fields emerge due to EP of the PM, and are unavoidable. For typical exposures through conventional EP protocols they are large enough to perturb the biochemical nature of organelles or even electroporate organelle membranes. Organelle EP has been described for supra-EP by nsPEFs (14,15,70), but is shown here to occur also for characteristic conventional EP pulses. Conventional EP may thus be large enough to even porate cytoplasmic organelles in cells.

This article is the first, to our knowledge, to quantify this possibility, demonstrating that nsPEFs for the EP of intracellular organelles are not necessary for intracellular manipulations. Several consequences have been presented here. The PM barrier to successful manipulation of signal transduction mechanisms can be surpassed and the biochemical nature of organelles may be controlled and manipulated even by conventional EP. Our results suggest that conventional EP pulses may elicit similar intracellular effects to those reported for nsPEFs, and thus provide a counter example to the assertion that only pulses with timescales shorter than τ_PM provide a unique way to achieve intracellular effects (5–13). A comparative understanding of the relative advantages and disadvantages of nsPEFs and longer pulse protocols will be of great interest, but remains to be determined.

There is, however, an essential and important difference between supra- and conventional organelle EP. The SE model of EP shows that pores expand insignificantly during nanosecond pulses (37,70). Pores remain small, whereas conventional pulses are sufficiently long for pores to expand to large radii (Fig. 2 here and Fig. S3 in the Supporting Material). This may have important consequences for molecular uptake and release, and for downstream cellular mechanisms, and needs to be further quantified.

The emergence of an intracellular electric field due to conventional EP was also previously demonstrated in Stewart et al. (14) by the use of the asymptotic EP model. More recently Mossop et al. (71) discussed the possibility of intracellular fields, however, not on the basis of an explicit EP model as presented here, but instead based on some assumptions about the effect of EP on the membrane resistivity. In contrast we quantify the intracellular electric field when dynamic pores are present explicitly and demonstrate its influence on the cell organelles.

Conventional EP pulses are broadly employed to deliver externally supplied molecules over a wide range of molecular sizes into a cell, with a strong emphasis on delivering genetic material. For this reason there is a need to optimize EP protocols for each cell and delivered molecule. Virtually all studies that focus on the process of EP state that the molecular mechanism is not completely understood. But we argue that a complete understanding of the molecular process is neither achievable in the foreseeable future—even the most sophisticated MD simulations use some approximations—or necessary.

For this reason, we suggest that the present goal should be to gain a sufficient understanding such that a specific outcome, for example the number of molecules being taken up, can be usefully predicted and ultimately controlled for research as well as for clinical and biotechnological applications. Advanced in silico methods, as presented here, predict the resulting distribution of pores sizes and thus the resulting membrane permeability and transport of any molecule for virtually any waveform, and might thus be used to perform rapid screening for many different EP conditions. The use of arbitrary waveform generators allows for waveform design, a capability that, although hardly discussed in the EP literature, may have been under consideration for commercial applications and may remain hidden for proprietary reasons.

Here we have shown that a logical conclusion of a cell system model comprised of individually plausible ingredients leads to the expectation of significant intracellular electric fields for conventional EP. Surprisingly, this general conclusion has received little attention. We argue that there are many possibilities worthy of consideration, and that existing and improving in silico methods should lead to new experimental studies of intracellular effects based on electric field pulses that are longer than the microsecond timescale.

Supporting Material

Four figures and four equations are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00313-9.