Figure 2.

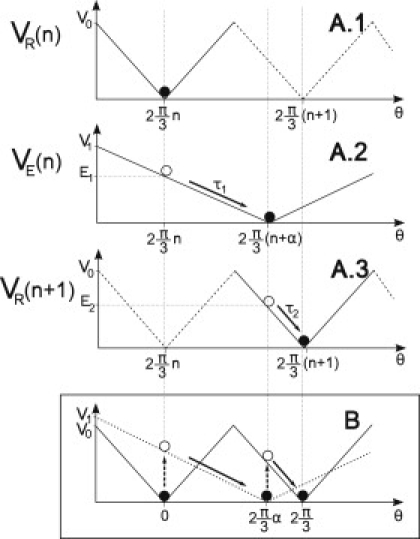
Dynamics of the two-states flashing ratchet model. (A1, A2, and A3) Detailed dynamics along the complete n^th step. The step involves two flashes of the potential that perform two different strokes. The n^th step starts when the motor switches the relaxed state potential V_R(θ, n) (A1) to the excited state potential V_E(θ, n) (A2) so V_E(θ, n) produces a torque τ₁ that moves the shaft to the minimum of V_E(n), therefore performing the first substep. The length of the first substep is determined by the parameter α (0.5 < α < 1). After this substep, the motor switches the potential from V_E(θ, n) (A2) to V_R(θ, n + 1) (A3) so V_R(θ, n + 1) produces a torque τ₂ that moves the shaft to the minimum of V_R(θ, n + 1), completing the second substep. The step is then finished and the shaft rests in the next minimum until a new excitation. In the scheme, the shaft is represented by a solid circle in the steady states and by an open circle in the transient ones. Solid lines show the potential acting on the γ-shaft in the corresponding state, and dashed lines indicate the periodicity of V_R. (B) Merger of panels A1, A2, and A3 for a compact visualization of the whole step including the relaxed (solid line) and the excited (dotted line) potentials. Initial minimum is chosen at θ = 0, allowing us to compare angular distances. Along the step, this is equivalent to chose n = 0. Dashed arrows indicate potential switching.