How Robust Are “Isolation with Migration” Analyses to Violations of the IM Model? A Simulation Study

Abstract

Methods developed over the past decade have made it possible to estimate molecular demographic parameters such as effective population size, divergence time, and gene flow with unprecedented accuracy and precision. However, they make simplifying assumptions about certain aspects of the species’ histories and the nature of the genetic data, and it is not clear how robust they are to violations of these assumptions. Here, we use simulated data sets to examine the effects of a number of violations of the “Isolation with Migration” (IM) model, including intralocus recombination, population structure, gene flow from an unsampled species, linkage among loci, and divergent selection, on demographic parameter estimates made using the program IMA. We also examine the effect of having data that fit a nucleotide substitution model other than the two relatively simple models available in IMA. We find that IMA estimates are generally quite robust to small to moderate violations of the IM model assumptions, comparable with what is often encountered in real-world scenarios. In particular, population structure within species, a condition encountered to some degree in virtually all species, has little effect on parameter estimates even for fairly high levels of structure. Likewise, most parameter estimates are robust to significant levels of recombination when data sets are pared down to apparently nonrecombining blocks, although substantial bias is introduced to several estimates when the entire data set with recombination is included. In contrast, a poor fit to the nucleotide substitution model can result in an increased error rate, in some cases due to a predictable bias and in other cases due to an increase in variance in parameter estimates among data sets simulated under the same conditions.

Introduction

Knowledge of molecular demographic parameters, such as current and historical effective population sizes, species divergence times, and rates of gene flow between populations or species, informs our understanding of many important phenomena, from the biogeographic histories of species groups to the process of speciation itself to the status of populations or species of conservation concern. However, reliable estimates of these parameters have historically been extremely difficult to make, in part because patterns of genetic diversity and differentiation can often be explained at least to a rough approximation by a wide range of divergence time and gene-flow combinations (Slatkin and Maddison 1989); and even in the absence of gene flow, estimates of divergence time can be confounded by changes in effective population size (Edwards and Beerli 2000). Advances in coalescent theory (Kingman 1982a, 1982b; Tavare 1984) have spurred the development of Bayesian and likelihood approaches to distinguish between “isolation” and “migration” models and to estimate demographic parameters (Nielsen and Wakeley 2001; Hey and Nielsen 2004). These approaches, which typically rely on Markov chain Monte Carlo (MCMC) simulations to sample among possible genealogical histories (Kuhner et al. 1995), have been incorporated into a number of computer programs (e.g., Nielsen 1998; Bahlo and Griffiths 2000; Beerli and Felsenstein 2001; Rannala and Yang 2003; Kuhner 2006; Drummond and Rambaut 2007; Heled and Drummond 2008; reviewed in Kuhner 2009), As a result, it is now feasible to document the molecular demographic histories of species representing virtually the entire diversity of life on earth, including viruses (Rambaut et al. 2008; Ramsden et al. 2009), bacteria (Moodley et al. 2009), fungi (Stukenbrock et al. 2007), animals (Alter et al. 2007; Gifford and Larson 2008), and plants (Lawton-Rauh et al. 2007; Strasburg and Rieseberg 2008), with unprecedented sophistication and precision.

Two related computer programs, IM and IMA (Hey and Nielsen 2004, 2007), are together perhaps the most widely used programs for estimating divergence times and levels of gene flow between recently diverged, hybridizing species. The “Isolation with Migration” (IM) model implemented in IM and IMA involves several simplifying assumptions, at least one of which is likely violated in virtually every natural system. These assumptions include no recombination within each locus, free recombination among all loci, no population structure within each species, no genetic contribution from unsampled populations or species, and selective neutrality. Violations of individual assumptions have been investigated or justified in various systems (e.g., Hey 2005; Bull et al. 2006; Strasburg and Rieseberg 2008). However, to our knowledge, there has been no rigorous, systematic examination of the robustness of the IM model to violations of these assumptions (but see Becquet and Przeworski 2009 for an examination of some violations related to timing of gene flow and to ancestral population structure).

Here, we present a simulation study examining the effects of a number of violations of the IM model on estimates of population sizes, divergence time, and rates of introgression made using IMA. We also examine the effects of analyzing sequences with patterns of nucleotide substitution that do not follow the infinite sites (IS, in which each mutation occurs at a unique site—Kimura 1969) or Hasegawa–Kishino–Yano (HKY, in which transition vs. transversion rates and base frequencies can be unequal—Hasegawa et al. 1985) substitution models available in IMA. We find that most biases introduced by IM model violations are small over what we consider to be biologically realistic conditions. Nucleotide substitution model violations also lead to biases that are relatively small in most cases; however, although averages of parameter estimates over multiple data sets are generally fairly close to the true value, certain substitution model violations can lead to significantly increased error rates due to an increased variance across data sets in parameter estimates. Overall, our findings indicate that the method of demographic inference implemented in the IMA program can be a powerful approach for estimating demographic parameters in many real-world scenarios, but researchers should give particular attention to patterns of nucleotide substitution in their data sets.

Materials and Methods

Simulated data sets, most involving one of several IM demographic model or nucleotide substitution model violations (see below), were created using one of four sequence simulation programs, and these simulated data sets were then used as input for IMA analyses. Most simulations were performed under the IS substitution model using the program make sample (MS—Hudson 2002). For each simulation condition, five independent data sets were simulated and analyzed as described below; for each data set, five loci of 500 base pairs (bp) each were simulated, and 40 sequences were sampled from each of two species. We chose data sets of five loci and 80 sequences in part because this is a reasonable if somewhat modest size for current real-world data sets: in papers published in the Journal Molecular Ecology using IM or IMA, the median numbers of loci and sequences were five and 154, respectively (data not shown). In addition, computational constraints prevented the use of larger data sets because of the number of separate runs required (testing of all conditions, including replicate data sets and replicate runs per data set as well as preliminary runs, necessitated roughly 600 runs).

Our baseline demographic model, hereafter referred to as the IM model, involves two species of equal effective population size (N_ef), 1 million individuals, that initially diverged 1 Ma from an ancestral species (which split evenly into the two descendant species) with an N_ef of 1 million and since then have exchanged genes at a constant, symmetrical rate of N_efm = 0.25. There is no population structure within either species, and neither species exchanges genetic material with any other unsampled species. In addition, there is no natural selection, no recombination within loci, and free recombination among loci. Parameters in the particular coalescent model simulated in IMA are 4N_efu for the three population sizes, m1/u, m2/u, and tu, where m1 and m2 are the rates of introgression per gene per generation into populations 1 and 2, respectively, t is the divergence time in generations, and u is the geometric mean of the mutation rates for each entire locus (not per bp) per generation. For computational convenience, we used a 1-year generation time. In order to translate these IMA parameter estimates into demographic quantities, we chose a mutation rate of 2.2 × 10⁻⁹ substitutions/site/year as a typical nuclear mutation rate for a wide range of organisms (Kumar and Subramanian 2002; Lynch 2006), corresponding to a rate of 1.1 × 10⁻⁶ substitutions/locus/year. Thus, our demographic quantities of 1 million for the three population sizes, 0.25 for N_efm in each direction, and 1 million years for divergence time correspond to IMA parameter values of 4.4, 0.22727, and 1.1, respectively. Note that these parameter values are dependent on the demographic quantities scaled by the mutation rate we chose, not on the specific demographic quantities themselves (in other words, other combinations of demographic quantities and mutation rates would result in the same parameter value estimates). Also note that N_ef2, N_efA, m, and t are parameterized differently in MS, as reflected in the MS commands we used (supplementary file S1, Supplementary Material online).

We tested seven violations of this IM model, as implemented in IMA: 1) intralocus recombination; 2) genetic exchange with a third unsampled species; 3) population structure within each species; 4) linkage among loci; 5) a divergent-selective sweep acting at one locus in one species; 6) incorrect DNA substitution model specification; and 7) more complex demographic scenarios involving unequal population sizes, asymmetric introgression rates, and population-size changes (population-size change is not considered in IMa, although it is included in the related program IM—Hey 2005). For each violation except selection, we simulated five to six different levels of severity; for selection, we simulated four divergent-selective sweeps that differed in timing and intensity (table 1). Details of the five violations are as follows:

1. Levels of intralocus recombination ranged from 0.005 to 0.05 per bp for the population recombination parameter ρ = 4N_efr (constant across loci). The incorporation of intralocus recombination resulted in violations of the IS substitution model in IMA based on the four-gamete criterion of Hudson and Kaplan (1985), necessitating the use of the HKY model instead. To avoid introducing any additional bias by simulating data under a different substitution model than was used in the IMA analysis, these data sets were generated by simulating trees under the appropriate demographic scenario in MS and then simulating sequence evolution along these trees under the HKY model in the program SEQ-GEN (Rambaut and Grassly 1997). A transition:transversion rate ratio of 1.6:1 (chosen as a fairly typical Tr:Tv ratio for nuclear DNA) was used for these simulations, and nucleotide frequencies were equal. For each level of recombination, the effects of paring the data set down to apparently nonrecombining blocks were also examined. Nonrecombining blocks were identified based on the four-gamete algorithm implemented in the program DNASP version 4.50.1 (Rozas et al. 2003), with sites containing three or more character states excluded. Apparently nonrecombining blocks were also made for HKY data sets that included no simulated recombination; in this case, violations were due to multiple mutations at the same site.

2. Levels of gene flow between the first focal species and a third unsampled species ranged from 0.1 to 1.0 for symmetrical N_efm values (gene flow did not occur between the second focal species and the third species). To ensure sufficient genetic divergence, the third species was simulated to have diverged from the common ancestor of the two focal species 5 My before present.

3. Population structure was simulated as four populations within each species, each of equal N_ef, 250,000, so that the sum of the individual population sizes was 1 million. Sequences were sampled equally from all populations, 10 each from the 4 populations within each species, maintaining an overall sample size of 40 sequences per species. Levels of structure were determined by varying rates of symmetrical gene flow among all pairs of populations within each species, with values ranging from N_efm = 0.1–2.0 (lower N_efm values correspond to more structure). To maintain consistent levels of gene flow between species, each population in one species exchanged genetic material with each population in the other species at a rate of N_efm = 0.015625, or 1/16 the IM model value of 0.25. Validation of this method of simulating population structure was performed by simulating a very high rate of gene flow among populations of the same species and verifying that parameter estimates converged on expected values for the IM model (data not shown).

4. For linkage among loci, simulations were performed using the program MSHOT (Hellenthal and Stephens 2007), which performs simulations similar to MS but incorporates recombination “hotspots.” The five loci were simulated as a single 2,500-bp “locus” with recombination hotspots at 500-bp intervals (between bp 500 and 501, 1,000 and 1,001, etc.). MSHOT requires that a baseline rate of recombination be specified and that hotspots then be defined based on recombination occurring at a multiple of that baseline rate. We chose a baseline recombination rate of ρ = 0.001 for the entire 2,500-bp locus, corresponding to a per bp ρ of 4 × 10⁻⁷ and a per bp r of 1 × 10⁻¹³, to ensure that this baseline level of recombination was too low to have an effect on IMA analyses. For two of the 125 loci simulated this way (five levels of linkage × five repeated simulations per linkage level × five loci per simulation), a recombination event occurred within a locus; these simulations were redone using a different starting seed. We then chose multipliers of this baseline level such that recombination rates between loci ranged from 0.005 to 0.1 per gene copy per generation, where a recombination rate of 0.5 per gene copy per generation would correspond to free recombination.

5. We simulated four types of divergent-selective sweeps, each occurring at a single locus within the first species. Sweeps were simulated as a short-term reduction in effective population size at the swept locus (Galtier et al. 2000), followed by a postsweep decrease in the effective migration rate at that locus. These included a weak and a strong sweep that occurred immediately after initial divergence and a weak and a strong sweep that occurred 10,000 years before present. A weak sweep was defined as a selective bottleneck of 1,000 individuals and a postsweep introgression rate for the selected locus of N_efm = 0.05 in each direction, or one-fifth the neutral rate. A strong sweep was defined as a selective bottleneck of 100 individuals and a postsweep introgression rate for the selected locus of N_efm = 0.01 in each direction, or 1/25 the neutral rate. In all cases, presweep introgression rates were N_efm = 0.25 for all loci, and postsweep introgression rates remained at N_efm = 0.25 for the four neutral loci. Selective bottlenecks lasted for 100 years, and N_ef changes at the swept locus occurred in a single generation.

6. We investigated the effect of nucleotide substitution model in two ways: First, five baseline IM simulations performed under the IS model in the program SIMDIV (http://lifesci.rutgers.edu/∼heylab/HeylabSoftware.htm#SIMDIV) were analyzed in IMA using both the HKY and IS models under the same conditions and with the same starting seeds, and the results of these analyses were compared. The sequence simulations were performed using SIMDIV instead of MS because MS only simulates ancestral and derived states without regard to base identity, but IMA analyses under the HKY substitution model require simulation of both transitions and transversions at realistic rate ratios (Hey J, personal communication). Simulations in SIMDIV were performed using a transition:transversion rate ratio of one and equal base frequencies, which are the only options available under the IS substitution model. It was not possible to perform the opposite comparison directly, with simulations performed under the HKY model in SEQ-GEN and analyzed in IMA using the IS substitution model, because of occurrences of multiple mutations at the same site. Therefore, we used the zero-recombination HKY data set that had been pared down to the largest apparently nonrecombining sequence blocks based on the four-gamete criterion for analysis in IMA using the IS substitution model. Second, we also took the trees from the five baseline IM simulations performed in MS and simulated sequence evolution along these trees under a more complex general time reversible (GTR; in which base frequencies and all six symmetrical substitution rates can be unequal—Tavare 1986) model in SEq-GEN. Five loci were simulated for each data set under GTR model parameters estimated using the program Modeltest version 3.7 (Posada and Crandall 1998) for five loci used in a previous molecular demographic study in sunflowers (Strasburg and Rieseberg 2008; GTR model parameters are given in SEQ-GEN commands in supplementary file S1, Supplementary Material online). These data sets were then analyzed in IMA using the HKY substitution model. For IS simulation/HKY analyses and HKY simulation/IS analyses, we compared the results of analyses using the wrong model with results using the correct model, rather than comparing them with the simulated demographic values; this allowed us to focus more explicitly on the effects of substitution model choice without the confounding effects of stochastic variation in the simulations. This was not possible for the GTR-simulated data analyzed using the HKY model, so in these analyses, results were compared with the simulated demographic values.

7. Finally, we simulated more complex demographic scenarios involving unequal population sizes, asymmetric introgression rates, and population-size changes. Our motivation for using a simple demographic scenario above was to more clearly isolate and document the effects of the various model violations; however, it may be the case that demographic complexity, such as is likely to be found in most real-world situations, may also create difficulties in parameter estimation. In particular, population-size change is not modeled in IMA, and so current effective population size estimates will likely be affected by the degree, timing, and rate of population growth. In these simulations, current N_efs were 2 million and 400,000 for the first and second species, respectively, the ancestral N_ef was 1 million, divergence time was 1 My, and rates of effective migration into the first and second species were N_efm = 0.4 and N_efm = 0.02, respectively. We simulated population-size changes in two ways: as exponential population growth from splitting to the present and as instantaneous population-size changes to the current sizes at splitting. There were no other violations of the IM model.

Table 1.

Summary of Simulations Performed.

Model Violation	# Simulations (39 Total)	Parameter, Simulated Values	Further Details
IM model (baseline – no violations), IS evolution	1	NA	IS simulation using MS; IS model specified in IMA
IM model, HKY evolution	1	NA	HKY simulation using SEQ-GEN based on trees simulated in MS; HKY model specified in IMA
IM model, IS evolution, HKY substitution model	1	NA	Same data sets, priors, and starting seeds as baseline IS runs, but with HKY model specified in IMA
IM model, HKY evolution, IS substitution model	1	NA	HKY simulation using SEQ-GEN based on trees simulated in MS; analyzed largest sequence blocks with no four-gamete test violations; IS model specified in IMA
IM model, GTR evolution, HKY substitution model	1	NA	GTR simulation using SEQ-GEN based on trees simulated in MS; HKY model specified in IMA
Intralocus recombination, full data set	6	ρ per bp = 0.005, 0.01, 0.02, 0.03, 0.04, 0.05	HKY simulation using SEQ-GEN based on trees simulated in MS; HKY model specified in IMA
Intralocus recombination, nonrecombining blocks	7	ρ per bp = 0, 0.005, 0.01, 0.02, 0.03, 0.04, 0.05	Four-gamete criterion used to identify recombination; HKY simulation using SEQ-GEN based on trees simulated in MS; HKY model specified in IMA
Introgression from third, unsampled species	5	Nefm between first focal species and third species = 0.1, 0.2, 0.3, 0.5, 1.0	5-Ma divergence time between third species and common ancestor of focal species; gene flow only with first focal species
Population structure	5	Nefm among populations within each species = 0.1, 0.2, 0.5, 1.0, 2.0	Four populations of equal size within each species
Linkage among loci	5	r among loci = 0.005, 0.01, 0.02, 0.05, 0.1
Divergent-selective sweep	4	Timing: 1 Ma, 10 kYA	Bottlenecks last 100 years; Nef changes are instantaneous; presweep, neutral Nefm = 0.25
		Bottleneck size: 1,000, 100
		Postsweep Nefm: 0.05, 0.01
IM model, IS evolution, more complex demography	2	NA	Population-size change simulated as instantaneous change or exponential growth

All 39 simulation conditions (summarized in table 1) were simulated five times. All MS, SEQ-GEN, MSHOT, and SIMDIV commands for the various simulations are given in supplementary file S1, Supplementary Material online. For each simulation, basic diversity summary statistics were calculated using DNASP version 4.50.1. The “0”s and “1”s in the MS/MSHOT output, corresponding to ancestral and derived character states at polymorphic sites, were arbitrarily reclassified to A's and T's, respectively, and additional A's were added to ensure that the length of each locus in the IMA analysis was 500 bp (for IS nonrecombining blocks simulations, invariant sites were placed between polymorphic sites according to position information given in MS/MSHOT in order to determine the sizes of nonrecombining blocks). All analyses were performed using the IS substitution model except as noted above. Inheritance scalars were set to one for all loci.

Each IMA analysis was run at least three times with different random number seeds to ensure convergence. Runs involved 10–20 independent chains with geometric heating and ranged from 4 to 32 million steps following a 100,000 step burn-in, and for all runs included in the analyses, the lowest effective sample size (ESS) among the parameters was at least 50, as recommended in the IMA documentation (in most cases, ESS values ranged from several hundreds to >10,000). Upper bounds of the prior distributions for each parameter were set based on the results of a preliminary run and were chosen to be at least ∼10 times higher than the “true” values (upper bounds were 10–14 million for the three population sizes, 8–20 My for divergence time and 0.0022 for m1 and m2). Priors were the same for all analyses. In most cases, posterior distributions converged within the prior range; exceptions (mostly for divergence-time estimates) are noted below. Results were highly consistent across the three runs for each simulated data set, and a single representative run is presented here.

Results

Average maximum likelihood estimates (MLEs) and 90% highest posterior density (HPD) intervals for the six demographic parameters, as well as information on posterior distribution completeness and accuracy, are given in tables 2–4. Biases in average MLEs for the six demographic parameters under various simulation conditions are shown graphically in figure 1, as is variation among data sets within each simulation condition. In addition, averaged summary statistics for the simulated loci are given in supplementary file S2, Supplementary Material online, and graphs of MLEs, HPD intervals, and coefficients of variation in MLE for the six parameters under various model violations and levels of severity are given in supplementary file S3, Supplementary Material online.

Table 2.

Simulation Results—Current Effective Population Sizes for Each Species.

	Current Nef, First Species, ×106 (1 million)				Current Nef, Second Species, ×106 (1 million)
Model	MLE	HPD90	# Completea	# Trueb	MLE	HPD90	# Completea	# Trueb
Baseline—IS	0.92	0.66–1.28	5	5	0.98	0.71–1.35	5	5
Baseline—HKY	0.94	0.66–1.30	5	4 (1,0)	1.03	0.73–1.41	5	5
Recombination, ρ = 0.005	1.13	0.83–1.51	5	4 (0,1)	1.27	0.95–1.67	5	3 (0,2)
Recombination, ρ = 0.01	1.35	1.01–1.78	5	2 (0,3)	1.37	1.02–1.80	5	3 (0,2)
Recombination, ρ = 0.02	1.52	1.14–1.98	5	2 (0,3)	1.70	1.30–2.20	5	0 (0,5)
Recombination, ρ = 0.03	2.00	1.56–2.56	5	0 (0,5)	2.31	1.81–2.93	5	0 (0,5)
Recombination, ρ = 0.04	2.35	1.84–2.98	5	0 (0,5)	2.66	2.10–3.36	5	0 (0,5)
Recombination, ρ = 0.05	2.88	2.29–3.62	5	0 (0,5)	2.97	2.35–3.75	5	0 (0,5)
NR blocks, ρ = 0	0.93	0.63–1.32	5	4 (1,0)	1.00	0.69–1.40	5	5
NR blocks, ρ = 0.005	0.83	0.54–1.23	5	3 (2,0)	0.97	0.67–1.38	5	4 (1,0)
NR blocks, ρ = 0.01	0.76	0.48–1.16	5	3 (2,0)	0.75	0.48–1.14	5	3 (2,0)
NR blocks, ρ = 0.02	0.82	0.51–1.26	5	4 (1,0)	0.81	0.51–1.25	5	5
NR blocks, ρ = 0.03	0.99	0.62–1.53	5	4 (1,0)	1.10	0.68–1.75	5	4 (1,0)
NR blocks, ρ = 0.04	0.81	0.48–1.32	5	5	0.95	0.57–1.54	5	5
NR blocks, ρ = 0.05	0.68	0.39–1.19	5	3 (2,0)	0.74	0.42–1.25	5	4 (1,0)
Third species g.f., Nefm = 0.1	1.15	0.85–1.53	5	5	0.83	0.59–1.14	5	4 (1,0)
Third species g.f., Nefm = 0.2	1.19	0.87–1.57	5	5	0.91	0.67–1.22	5	5
Third species g.f., Nefm = 0.3	1.07	0.79–1.42	5	5	1.00	0.75–1.31	5	4 (1,0)
Third species g.f., Nefm = 0.5	1.41	1.07–1.83	5	3 (0,2)	0.84	0.60–1.13	5	4 (1,0)
Third species g.f., Nefm = 1.0	1.29	0.98–1.69	5	2 (0,3)	0.80	0.57–1.09	5	4 (1,0)
Pop. structure, Nefm = 2.0	0.95	0.68–1.31	5	5	0.91	0.65–1.26	5	5
Pop. structure, Nefm = 1.0	0.99	0.71–1.35	5	5	0.97	0.70–1.35	5	5
Pop. structure, Nefm = 0.5	0.93	0.67–1.27	5	5	1.05	0.77–1.41	5	4 (0,1)
Pop. structure, Nefm = 0.2	1.14	0.82–1.55	5	4 (0,1)	1.25	0.90–1.68	5	4 (0,1)
Pop. structure, Nefm = 0.1	1.02	0.74–1.37	5	4 (0,1)	0.96	0.69–1.32	5	5
Linkage, r = 0.1	0.89	0.62–1.21	5	4 (1,0)	0.96	0.69–1.30	5	5
Linkage, r = 0.05	0.87	0.61–1.22	5	5	1.04	0.75–1.42	5	5
Linkage, r = 0.02	0.98	0.69–1.32	5	5	0.81	0.56–1.13	5	4 (1,0)
Linkage, r = 0.01	1.01	0.73–1.35	5	5	0.94	0.67–1.28	5	5
Linkage, r = 0.005	0.97	0.69–1.31	5	5	0.83	0.58–1.16	5	4 (1,0)
Selection—early weak	1.02	0.74–1.39	5	5	1.02	0.74–1.39	5	5
Selection—early strong	0.89	0.64–1.22	5	5	0.83	0.60–1.14	5	3 (2,0)
Selection—late weak	0.68	0.46–0.96	5	1 (4,0)	0.94	0.66–1.30	5	5
Selection—late strong	0.53	0.35–0.78	5	1 (4,0)	0.90	0.64–1.25	5	4 (1,0)

Values listed for MLE and HPD90 interval are averages over five independent simulated data sets. Numbers in parentheses next to parameters are values used in simulations.

^aNumber of runs for which the posterior probability distribution has zero density at the prior upper bound.

^bNumber of runs for which the HPD interval contains the true value. Numbers in parentheses are the number of simulated values that were significantly lower and higher than the true value, respectively.

Table 4.

Simulation Results—Effective Migration Rates.

	Nefm, Second Species → First Species (0.25)				Nefm, First Species → Second Species (0.25)
Model	MLE	HPD90	# Completea	# Trueb	MLE	HPD90	# Completea	# Trueb
Baseline—IS	0.24	0.06–0.58	5	4 (0,1)	0.17	0.04–0.53	5	5
Baseline—HKY	0.37	0.11–0.84	5	5	0.18	0.03–0.58	5	5
Recombination, ρ = 0.005	0.31	0.10–0.63	5	5	0.15	0.05–0.44	5	4 (1,0)
Recombination, ρ = 0.01	0.25	0.07–0.57	5	5	0.21	0.05–0.55	5	5
Recombination, ρ = 0.02	0.41	0.17–0.82	5	4 (0,1)	0.21	0.03–0.55	5	5
Recombination, ρ = 0.03	0.28	0.10–0.57	5	5	0.35	0.14–0.69	5	5
Recombination, ρ = 0.04	0.28	0.09–0.60	5	5	0.22	0.05–0.55	5	5
Recombination, ρ = 0.05	0.28	0.09–0.63	5	5	0.39	0.14–0.77	5	4 (0,1)
NR blocks, ρ = 0	0.37	0.11–0.90	5	5	0.16	0.02–0.57	5	5
NR blocks, ρ = 0.005	0.29	0.07–0.74	5	5	0.09	0.01–0.43	5	4 (1,0)
NR blocks, ρ = 0.01	0.17	0.03–0.57	5	5	0.19	0.02–0.65	5	4 (1,0)
NR blocks, ρ = 0.02	0.26	0.05–0.78	5	5	0.24	0.06–0.78	5	5
NR blocks, ρ = 0.03	0.12	0.02–0.71	5	5	0.26	0.01–1.15	5	5
NR blocks, ρ = 0.04	0.12	0.01–0.62	5	5	0.22	0.02–0.89	5	5
NR blocks, ρ = 0.05	0.16	0.02–0.91	5	5	0.31	0.04–1.13	5	5
Third species g.f., Nefm = 0.1	0.21	0.03–0.68	5	4 (1,0)	0.19	0.04–0.59	5	5
Third species g.f., Nefm = 0.2	0.31	0.08–0.62	5	5	0.25	0.09–0.55	5	4 (1,0)
Third species g.f., Nefm = 0.3	0.33	0.15–0.65	5	3 (0,2)	0.04	0.00–0.20	5	2 (3,0)
Third species g.f., Nefm = 0.5	0.48	0.23–0.84	5	3 (0,2)	0.16	0.03–0.39	5	4 (1,0)
Third species g.f., Nefm = 1.0	0.43	0.14–0.79	5	3 (0,2)	0.15	0.03–0.40	5	5
Pop. structure, Nefm = 2.0	0.18	0.02–0.56	5	5	0.34	0.09–0.74	5	4 (0,1)
Pop. structure, Nefm = 1.0	0.23	0.04–0.71	5	5	0.37	0.09–0.83	5	5
Pop. structure, Nefm = 0.5	0.37	0.15–0.73	5	5	0.21	0.06–0.53	5	4 (1,0)
Pop. structure, Nefm = 0.2	0.30	0.07–0.76	5	5	0.22	0.05–0.72	5	5
Pop. structure, Nefm = 0.1	0.25	0.04–0.60	5	5	0.40	0.15–0.85	5	4 (0,1)
Linkage, r = 0.1	0.25	0.07–0.55	5	5	0.21	0.07–0.51	5	4 (1,0)
Linkage, r = 0.05	0.34	0.10–0.72	5	5	0.16	0.02–0.55	5	5
Linkage, r = 0.02	0.14	0.03–0.44	5	5	0.28	0.11–0.58	5	3 (1,1)
Linkage, r = 0.01	0.15	0.04–0.44	5	5	0.25	0.09–0.54	5	5
Linkage, r = 0.005	0.21	0.07–0.49	5	4 (1,0)	0.31	0.11–0.60	5	5
Selection—early weak	0.28	0.08–0.67	5	5	0.21	0.03–0.54	5	5
Selection—early strong	0.19	0.04–0.46	5	5	0.14	0.02–0.39	5	4 (1,0)
Selection—late weak	0.28	0.08–0.65	5	5	0.29	0.07–0.65	5	5
Selection—late strong	0.23	0.07–0.56	5	5	0.21	0.07–0.56	5	5

Values listed for MLE and HPD90 interval are averages over five independent simulated data sets. Numbers in parentheses next to parameters are values used in simulations.

^aNumber of runs for which the posterior probability distribution has zero density at the prior upper bound.

^bNumber of runs for which the HPD interval contains the true value. Numbers in parentheses are the number of simulated values that were significantly lower and higher than the true value, respectively.

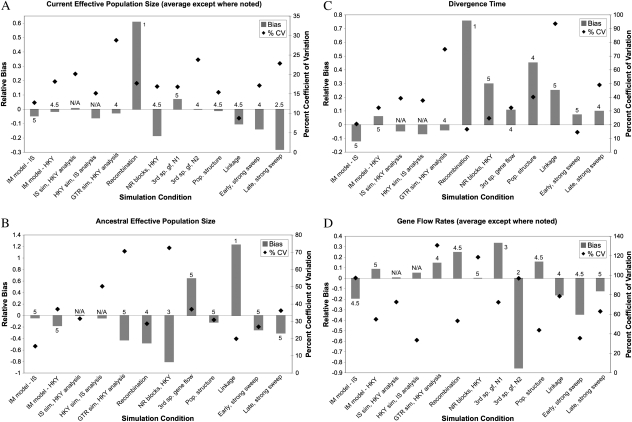
FIG. 1.

Relative bias based on average MLE and coefficient of variation (CV) in MLE values for various simulation conditions in estimates of (A) current effective population size, averaged over the two species (values reported separately for third species gene flow); (B) ancestral effective population size; (C) divergence time; and (D) interspecific gene flow, averaged over the two species (values reported separately for third species gene flow). Bias is calculated as (average MLE − true value)/(true value). For violations with multiple levels of severity, a single intermediate level was used here: ρ = 0.02 per bp for recombination violations, N_efm = 0.3 for third species gene flow, N_efm = 0.5 for population structure, r = 0.02 for interlocus linkage. Data for all levels of severity are shown in supplementary file S3, Supplementary Material online. Numbers above or next to bars are the number of replicates out of five (averaged over the two species or two directions for current N_ef and gene flow rates, respectively, except for third species gene flow) for which the HPD interval contains the true value. IS-simulated data analyzed with the HKY model and HKY-simulated data analyzed with the IS model were compared with analyses using the correct model rather than to the true values, so no numbers are given in those cases. Note that bias and CV are plotted on different axes.

No Violations of the IM Demographic Model

When there were no violations of the IM model, IMA results were very consistent with expectations based on simulation parameters, both for IS and HKY sequence evolution (tables 2–4, supplementary file S3A, Supplementary Material online). In each case, 29 of the 30 HPD intervals (six parameters × five independent simulated data sets) contained the true value, well within expected error rates based on chance. The average MLEs for all three N_ef estimates were fairly close to the true value of 1 million for both substitution models, as were the average MLEs for divergence time. Average MLEs for gene-flow rates varied somewhat more from the true values of N_efm = 0.25 in each direction, but individual MLEs both above and below the true value were recorded, with no obvious trend toward a bias in either direction. All posterior distributions were completely contained within the prior bounds with the exception of divergence time distributions, which often contained low plateaus that extended from a sharp peak near the true value to the upper bound of the prior. Divergence time posteriors for four IS data sets and three HKY data sets contained these plateaus; HPD estimates for these data sets should be interpreted with caution because the posterior distribution has nonzero density at the prior upper bound. But with few exceptions (discussed below), these incomplete divergence time posterior distributions consisted of sharp peaks in the vicinity of the true value followed by very low to moderately sized plateaus (well under the height of the MLE peak) that extended to 10–20 times the true value without an additional peak in the higher range; we therefore consider the MLEs for these divergence-time estimates to be reliable.

Intralocus Recombination

Recombination was addressed in two ways—by simulating various levels of recombination under HKY evolution and including the entire data sets in the IMA analysis, and by taking these same data sets but only including the largest nonrecombining blocks in the IMA analysis. When all data are included, results are largely consistent with previous reports for N_ef estimates (Bull et al. 2006; Strasburg and Rieseberg 2008). Current N_ef estimates show a roughly linear increase with recombination rate (table 2, supplementary file S3B, Supplementary Material online). Even at the lowest recombination level of ρ = 0.005 per bp, 3 of 10 current N_ef HPD intervals do not include the true values; for recombination levels above 0.02, average MLEs are two to three times above the true value, and no HPD intervals include the true values. Ancestral N_ef estimates are biased in the opposite direction, with average MLEs roughly 50–60% of the true value for all levels of recombination, and eight of 25 HPD intervals do not include the true value (table 3). In contrast to previous reports (Bull et al. 2006; Strasburg and Rieseberg 2008), we see a significant effect of recombination on divergence-time estimates—for all recombination levels, the average HPD_Lo was greater than the true value, and no HPD intervals included the true value for recombination levels of above 0.02 (table 3). HPD intervals for both ancestral N_ef and divergence time became smaller with increasing recombination (supplementary file S3B, Supplementary Material online). Only one divergence time posterior distribution has nonzero density at the prior upper bound for full data sets containing recombination, in contrast to the low plateaus seen in most zero-recombination HKY data sets. Recombination had little effect on estimates of gene flow; all average MLEs are fairly close to the true values (table 4).

Table 3.

Simulation Results—Ancestral Effective Population Size and Divergence Time.

	Ancestral Nef, ×06 (1 million)				Divergence Time, ×106 (1 million)
Model	MLE	HPD90	# Completea	# Trueb	MLE	HPD90	# Completea	# Trueb
Baseline—IS	0.96	0.16–4.26	5	5	0.88	0.46–7.53	1	5
Baseline—HKY	0.82	0.15–4.50	5	5	1.06	0.48–6.46	2	5
Recombination, ρ = 0.005	0.55	0.10–1.36	5	4 (1,0)	1.93	0.93–3.34	4	3 (0,2)
Recombination, ρ = 0.01	0.60	0.23–1.25	5	4 (1,0)	1.78	1.01–2.77	5	3 (0,2)
Recombination, ρ = 0.02	0.52	0.16–1.07	5	4 (1,0)	1.76	1.18–2.72	5	1 (0,4)
Recombination, ρ = 0.03	0.53	0.19–1.07	5	3 (2,0)	2.00	1.48–2.75	5	0 (0,5)
Recombination, ρ = 0.04	0.61	0.27–1.15	5	3 (2,0)	1.99	1.48–2.63	5	0 (0,5)
Recombination, ρ = 0.05	0.54	0.24–0.99	5	3 (2,0)	1.95	1.54–2.45	5	0 (0,5)
NR blocks, ρ = 0	0.75	0.01–5.87	5	4 (1,0)	1.16	0.55–8.34	1	5
NR blocks, ρ = 0.005	0.48	0.01–6.67	5	5	1.12	0.65–11.52	1	4 (0,1)
NR blocks, ρ = 0.01	0.45	0.01–7.99	5	5	1.13	0.41–13.19	0	5
NR blocks, ρ = 0.02	0.20	0.02–6.22	5	3 (2,0)	1.30	0.55–11.24	2	5
NR blocks, ρ = 0.03	0.27	0.01–5.07	5	3 (2,0)	1.20	0.54–12.78	2	5
NR blocks, ρ = 0.04	0.25	0.02–6.34	5	3 (2,0)	1.16	0.42–13.41	2	5
NR blocks, ρ = 0.05	0.20	0.01–7.97	5	5	1.09	0.39–20.78	0	5
Third species g.f., Nefm = 0.1	1.49	0.27–5.99	5	4 (0,1)	0.96	0.49–8.00	0	5
Third species g.f., Nefm = 0.2	1.34	0.25–9.42	5	5	1.35	0.89–9.09	0	3 (0,2)
Third species g.f., Nefm = 0.3	1.65	0.21–5.41	5	5	1.11	0.79–7.27	0	4 (0,1)
Third species g.f., Nefm = 0.5	1.01	0.01–3.84	5	5	0.94	0.70–7.27	0	5
Third species g.f., Nefm = 1.0	1.68	0.01–6.03	5	5	1.01	0.59–9.09	0	3 (0,2)
Pop. structure, Nefm = 2.0	0.86	0.17–5.14	5	5	0.91	0.47–6.00	2	5
Pop. structure, Nefm = 1.0	1.07	0.19–5.39	5	5	1.05	0.49–7.02	1	5
Pop. structure, Nefm = 0.5	0.88	0.08–5.50	5	5	1.45	0.77–7.66	1	4 (0,1)
Pop. structure, Nefm = 0.2	1.03	0.35–2.40	5	5	0.94	0.51–4.42	3	4 (1,0)
Pop. structure, Nefm = 0.1	0.83	0.05–6.13	5	4 (1,0)	1.19	0.63–7.63	1	5
Linkage, r = 0.1	1.74	0.67–9.43	5	4 (0,1)	0.91	0.52–9.09	0	5
Linkage, r = 0.05	1.36	0.39–8.89	3	4 (0,1)	0.95	0.55–9.09	0	5
Linkage, r = 0.02	2.23	1.04–6.83	5	1 (0,4)	1.25	0.44–7.65	2	5
Linkage, r = 0.01	1.59	0.49–8.88	3	4 (0,1)	1.03	0.62–7.50	1	4 (0,1)
Linkage, r = 0.005	2.13	0.69–9.76	5	3 (0,2)	1.44	0.59–8.97	0	5
Selection—early weak	0.56	0.02–3.09	5	3 (2,0)	1.27	0.76–5.09	3	3 (0,2)
Selection—early strong	0.75	0.10–4.02	5	5	1.07	0.62–7.65	1	5
Selection—late weak	0.81	0.07–6.05	5	5	1.02	0.52–7.24	0	4 (0,1)
Selection—late strong	0.69	0.01–6.08	5	5	1.10	0.60–8.51	0	4 (0,1)

Values listed for MLE and HPD90 interval are averages over five independent simulated data sets. Numbers in parentheses next to parameters are values used in simulations.

^aNumber of runs for which the posterior probability distribution has zero density at the prior upper bound.

^bNumber of runs for which the HPD interval contains the true value. Numbers in parentheses are the number of simulated values that were significantly lower and higher than the true value, respectively.

When data sets are pared down to nonrecombining blocks, current N_efs are overall biased somewhat low, as would be expected if the removal of regions showing recombination biases the data set toward regions of lower genetic variation (table 2, supplementary file S3C, Supplementary Material online). The bias does not appear to be very strong in terms of average MLE, although 13 of 60 (two current population sizes × five data sets × six recombination levels) HPD intervals do not contain the true value of 1 million, more than twice as many as would be expected by chance; and in every case, the true value is higher than the HPD interval (table 2). Ancestral N_ef estimates are also biased downward, and in this case, the bias is considerably more pronounced; average MLEs rapidly drop to approximately one-fourth to one-fifth the true value, and 6 of 30 HPD intervals do not contain the true value (all biased low; table 3). Divergence time and gene flow MLEs are largely unaffected, but HPD intervals for these parameters as well as population size parameters generally become larger with increasing recombination; this is also to be expected, as increasing levels of recombination yield increasingly smaller nonrecombining blocks, and thus increasingly smaller data sets (see supplementary file S2, Supplementary Material online) containing less information. When data sets with no true recombination are pared down to apparently nonrecombining blocks, the effect, if any, is extremely small for the population sizes and mutation rates simulated here.

Gene Flow with a Third Unsampled Species

When simulations contain gene flow between the first focal species and a third, unsampled species, a number of parameters are affected (supplementary file S3D, Supplementary Material online). Current N_ef estimates for the first focal species increase with increasing gene flow, whereas estimates for the second focal species decrease (table 2). For low to moderate levels of introgression that are probably realistic for most hybridizing species, the bias in focal species current N_ef estimates is minimal. But for higher levels (N_efm of 0.5 or greater), the effect becomes more noticeable. Half of the first species current N_ef HPD intervals for these levels are above the true value, and 20% of the second species current N_ef HPD intervals are below the true value. Third species gene flow also increases ancestral N_ef estimates, as well as increasing the width of ancestral N_ef HPD intervals (table 3). At the highest gene flow levels, all HPD intervals include the true value, but the average HPD_Lo is under 10,000, and the average HPD_Hi is greater than 6 million. There also appears to be some upward bias in divergence-time estimates, even for moderate levels of gene flow (N_efm of 0.2; table 3). Although this bias is quite small in terms of average MLEs, five of 20 HPD intervals for N_efm ≥ 0.2 are above the true value. This is presumably due to the fact that some sequences sampled from the first focal species are migrants from the third species (or descended from such migrants), which has a much more ancient divergence from the second species. Finally, third species gene flow causes an increase in estimated gene flow from the second focal species into the first focal species and a decrease in gene flow estimates in the opposite direction (table 4). These biases are small for low levels of gene flow (N_efm ≤ 0.2), but for higher levels, they become substantial. The bias in gene flow from the first to the second species in figure 1D for the intermediate level of N_efm = 0.3 appears extremely strong; in fact, this is the largest bias of all levels of severity (table 4), and as such may be somewhat unrepresentative. This pattern would presumably disappear with more simulations.

Population Structure

Most demographic parameter estimates in IMA are fairly robust to population structure within each species, at least over a range that we consider to be realistic for most species (down to N_efm of 0.1 among conspecific populations; supplementary file S3E, Supplementary Material online). There is no obvious bias in any of the six parameters, and rates at which HPD intervals do not include the true value are comparable with data sets with no IM model violations (tables 2–4).

Linkage among Loci

When the five loci are linked to some degree, the most obvious consequence is an upward bias in estimates of the ancestral N_ef (table 3, supplementary file S3F, Supplementary Material online); average MLEs increase to roughly twice the true value for recombination rates below 0.02 per gene copy per generation, and more than a third of HPD intervals for data sets with linkage among loci were higher than the true value. This is surprising, as linkage among loci is expected to increase the correlation in coalescence times among loci (McVean 2002), which should result in a downward bias in ancestral N_ef estimates. This is the most counterintuitive result of our simulations, and further study is needed to verify and, if necessary, explain it. Other parameters have average MLEs close to the true value and relatively few HPD intervals that do not contain the true value for all levels of linkage tested here.

Selection

We simulated a divergent-selective sweep at one locus in one species under four conditions: an early, weak sweep; an early, strong sweep; a late, weak sweep; and a late, strong sweep (supplementary file S3G, Supplementary Material online). As expected, late sweeps had considerably more impact on current N_ef estimates for the species undergoing the sweep than did early sweeps—all HPD intervals for early sweeps contained the true value, whereas only one of five HPD intervals for both late weak and late strong sweeps contained the true value (table 2). In contrast, early sweeps, after which gene flow is reduced for a much greater proportion of the species’ history, had a greater impact on estimates of gene flow (table 4). Average MLEs of N_efm are 13% lower and 25% lower for early weak versus late weak and early strong versus late strong sweeps, respectively. However, only one N_efm HPD interval did not include the presweep/neutral value—an estimate for one early strong simulation, in which the presweep value was higher than the HPD interval.

Incorrect Nucleotide Substitution Model

When data sets were simulated under the IS model but analyzed in IMA under the HKY model, biases are relatively small for all parameters; the most significant one is a roughly 5% decrease in average divergence-time MLE, although all divergence-time posteriors are still broadly overlapping (table 5, supplementary file S3A, Supplementary Material online). When HKY-simulated data sets were pared down to the largest apparently nonrecombining blocks and analyzed under the IS model in IMA, the biases were somewhat larger but still not excessive; four of the six parameter biases were larger than the largest bias for IS simulation/HKY analysis, but all were under 10%.

Table 5.

Simulation Results for Incorrect Nucleotide Substitution Models.

	IS Sim, HKY Analysis	HKY Sim, IS Analysis	GTR Simulation, HKY Analysis
Parameter	Relative Bias	Relative Bias	MLE	HPD90	# Completea	# Trueb
Current Nef, Sp. #1 (1 million)	0.008	−0.052	1.07	0.77–1.49	5	4 (0,1)
Current Nef, Sp. #2 (1 million)	0.005	−0.070	0.87	0.59–1.24	5	4 (1,0)
Ancestral Nef (1 million)	0.007	−0.044	0.57	0.08–4.33	5	5
Div. Time (1 My)	−0.046	−0.067	0.96	0.53–7.52	1	4 (0.1)
Nefm, Sp. #2 → Sp. #1 (0.25)	0.015	0.006	0.42	0.10–0.90	5	4 (1,0)
Nefm, Sp. #1 → Sp. #2 (0.25)	−0.003	0.097	0.16	0.05–0.91	5	4 (1,0)

For IS simulations analyzed using the HKY model in IMA and HKY simulations analyzed using the IS model in IMA, results are presented as relative bias for the various parameters, calculated as (average MLE using incorrect model – average MLE using correct model)/(average MLE using correct model). Because this was not possible for GTR simulations analyzed using the HKY model in IMA, these results are presented in the same format as tables 2–4. Numbers in parentheses next to parameters are values used in simulations.

^aNumber of runs for which the posterior probability distribution has zero density at the prior upper bound.

^bNumbers in parentheses are the number of simulated values that were significantly lower and higher than the true value, respectively.

Bias introduced by simulating data under a GTR model based on real DNA sequence data and analyzing it under the HKY model was relatively small for most parameters (table 5, supplementary file S3A, Supplementary Material online); however, ancestral effective population sizes were poorly estimated (the average MLE was more than 40% below the true value, although all ancestral N_ef HPD intervals contained the true value because they were exceptionally broad), and variation among data sets was high. Whereas only 2 of 60 HPD intervals for IS- and HKY-simulated data sets did not contain the true parameter value, 5 of 30 HPD intervals for GTR-simulated data sets analyzed using the HKY model did not contain the true parameter value, an error rate five times higher than when the model specified in IMA is accurate and 67% higher than expected by chance with a 90% HPD interval. This increase in variation among data sets is also reflected in the fact that GTR-simulated data sets have the highest coefficients of variation among the substitution model tests for all parameter estimates, usually by a wide margin (fig. 1).

Complex Demographic Scenarios

We also simulated data sets under a demographic scenario involving unequal population sizes and asymmetric introgression rates (table 6, supplementary file S3H, Supplementary Material online). When population sizes change to current values instantaneously at the time of initial divergence and are stable thereafter, accuracy of parameter estimates is comparable with the simple demographic scenario. However, under a scenario of exponential population growth since initial divergence resulting in the same current N_efs, current population size estimates are biased downward. Accuracy of other parameter estimates is comparable with the simple demographic scenario.

Table 6.

Simulation Results for More Complex Demographic Scenarios.

	Exponential Growth				Instantaneous Pop Size Change
Parameter	MLE	HPD90	# Completea	# Trueb	MLE	HPD90	# Completea	# Trueb
Current Nef, Sp. #1, ×106 (2 million)	1.29	0.94–1.85	5	1 (4,0)	1.92	1.45–2.54	5	5
Current Nef, Sp. #2, ×106 (400,000)	0.31	0.20–0.46	5	4 (1,0)	0.35	0.24–0.51	5	4 (1,0)
Ancestral Nef, ×106 (1 million)	1.05	0.27–9.37	4	4 (0,1)	0.78	0.13–6.25	5	5
Div. Time, ×106 (1 My)	0.91	0.54–9.09	0	5	1.22	0.66–6.26	2	5
Nefm, Sp. #2 → Sp. #1 (0.4)	0.41	0.13–0.75	5	5	0.50	0.20–0.94	5	4 (0,1)
Nefm, Sp. #1 → Sp. #2 (0.02)	0.02	0.00–0.12	5	5	0.03	0.00–0.13	5	5

Values listed for MLE and HPD90 interval are averages over five independent simulated data sets. Numbers in parentheses next to parameters are values used in simulations.

^aNumber of runs for which the posterior probability distribution has zero density at the prior upper bound.

^bNumbers in parentheses are the number of simulated values that were significantly lower and higher than true value, respectively.

Posterior Distribution Bimodality

In 20 cases from all simulation conditions (or 10.3% of 195 data sets—39 simulation conditions × five replicates per condition; see table 1), the posterior probability density distributions for divergence time were such that there was a smaller peak in probability in the general vicinity of the true value of 1 My, then a larger peak or slowly rising tail well above that range (generally at 5 My or greater; graphs of the marginal posterior probability densities for these 20 data sets are given in supplementary file S4, Supplementary Material online). In these cases, we took the divergence-time value associated with the smaller peak as the MLE, so as not to create an artificial upward bias in divergence-time estimates for these data sets. We consider this to be at least roughly analogous to setting the upper bound of the prior distribution at a biologically meaningful level, even if the posterior distribution has nonzero density at that upper bound (Hey 2005); in most cases, researchers are likely to know based on independent information that divergence-time estimates 5–10 times larger than the true divergence time are not biologically realistic, even if the true divergence time itself is not known precisely. Bimodal posterior distributions in particular should be interpreted with care, as they may represent two alternative demographic histories with significant likelihoods—an older divergence/higher gene flow scenario, and a more recent divergence/lower gene flow scenario. We see two distinct peaks (as opposed to one peak and a slowly rising tail) in 4 of these 20 data sets, but in none of them are either of the gene flow posteriors bimodal. In all but one case, the modified MLE was included within the original HPD interval, and the original HPD intervals are reported here. For that case, the modified MLE was below the HPD interval, and for the calculations in table 3, the low end of the HPD interval was set to the modified MLE.

Interestingly, more than half (11 of 20) of these data sets, and two of the four bimodal distributions, are from simulations involving gene flow with a third unsampled species, all at levels of N_efm ≥ 0.2. In the two bimodal distributions, the second peak is at roughly 5 My, which is the simulated divergence time between the third species and the common ancestor of the two focal species. It is possible that the presence of these more divergent alleles from the third species in the first species’ gene pool contributes to this second peak.

Computation Time

Analyses were run on several different personal computers and computing clusters with varying processor speeds. A representative analysis run on Indiana University's Quarry cluster using a 2.0-GHz quad-core Intel Xeon processor and using the IS substitution model ran at approximately 150,000 steps/h. We regularly ran nine analyses at a time on an Intel Mac with two 3.0-GHz quad-core Intel Xeon processors, and these analyses using the IS substitution model ran at approximately 90,000 steps/h. For the same substitution model, there was relatively little rate variation among different data sets (not counting pared down nonrecombining data sets); however, analyses run using the HKY substitution model were 50–60% slower than those using the IS model. Speed was also affected by the length of the sequences—analyses using a nonrecombining data set with an average locus length of 285 bp were approximately 30% faster than analyses using the full data set from which they were derived. The number of steps required to achieve satisfactory ESS values ranged from 4 million to 32 million, so the amount of time required also varied greatly, from roughly 2 days to more than 2 weeks.

Discussion

Accurate reconstruction of the demographic history of populations is required to address numerous issues in evolutionary biology, ranging from the role of gene flow during and after the initial divergence of lineages (Hey 2006), to inferences in bacterial and viral evolutionary epidemiology (Rambaut et al. 2008), to informed decisions on how to most effectively manage endangered populations and species (Hansen et al. 2008; Valdiosera et al. 2008). Analytical methods such as those discussed here allow more detailed inferences about demographic history than were possible in the past. However, there has been an ongoing need for an examination of their power and reliability under conditions likely to be encountered in natural systems. Important questions to be addressed include the power of IMA and related methods to detect low levels of gene flow (e.g., Nielsen and Wakeley 2001), the likelihood of false inferences of gene flow (e.g., Becquet and Przeworski 2009), the appropriateness of inferring timing of gene flow or mode of speciation based on these analyses (e.g., Niemiller et al. 2008), and optimal locus- and individual-sampling schemes (e.g., Felsenstein 2006). Here, we have addressed the robustness of IMa inferences to violations of the IM model.

Specific violations of the model, such as population structure (Hey 2005) and recombination (Strasburg and Rieseberg 2008) have been addressed in some cases. Muster et al. (2009) used simulated data sets in conjunction with IMa analyses of real data to test whether levels of gene flow inferred by IMa were consistent with various continuous or episodic migration scenarios. Likewise, Becquet and Przeworski (2009) performed a simulation study of IM and their program MIMAR (Becquet and Przeworski 2007) in which they examined the effects of ancestral population structure and temporal variation in introgression rates, but other violations of the IM model were not addressed.

We have simulated numerous violations of the IM model to varying degrees of severity, from minimal violations, at least one of which is likely found in most if not all real-world data sets (e.g., a small amount of population structure within species) to levels of severity that would rarely be expected in real-world data sets (e.g., strong linkage among all loci or introgression at a rate of N_efm = 1 with a third species). For moderate demographic model violations, IMA is reasonably robust for most parameters. For example, perhaps the most common violation of the IM model is population structure within one or both species. Population structure results in an effective size for the species as a whole that is greater than the sum of the individual population sizes, and the increase is inversely proportional to the migration rate among populations (Wright 1943; Hey 1991; Nei and Takahata 1993). Theoretical work by Wakeley (1998, 2000, 2001) indicates that biases in divergence time and gene flow estimates are also expected, although this work assumes a large number of populations within each species, and it is not clear how it would apply when this assumption is not met (Wakeley 2000). We simulated levels of population structure as strong as N_efm levels down to 0.1 among populations within each species (more than 90% of species have intraspecific gene flow levels of 0.1 or higher—Morjan and Rieseberg 2004) and found essentially no bias in any of the six estimated parameters (see tables 2–4). Likewise, moderate levels of gene flow with a third unsampled species (e.g., N_efm ≤ 0.2), which are unlikely to be exceeded by nonsister species in most systems (but see, e.g., Lawton-Rauh et al. 2007; Strasburg and Rieseberg 2008), produce relatively modest biases.

When recombination is not accounted for in our analyses, it creates substantial biases in all parameter estimates except gene flow, with the most dramatic biases being in current N_efs and divergence time. Ignoring recombination is expected to create biases in a number of parameter estimates (Schierup and Hein 2000). Current N_ef estimates are biased upward as variation actually caused by recombination is inferred to have been caused by mutation. Recombination also creates patterns similar to exponential growth in haplotype trees, which may help explain a downward bias in ancestral N_ef for a given set of current N_ef values. Likewise, divergence-time estimates are expected to be biased upward (Schierup and Hein 2000), a pattern we see in our analyses. However, paring down the data sets to apparently nonrecombining blocks effectively removes most of these biases, with the conspicuous exception of ancestral N_ef.

Linkage among loci is probably the IM model violation tested here that is least likely to be a concern for most real-world data sets. For many species, linkage maps allow researchers to confirm that their chosen loci are unlinked; and even in the absence of a map, it is unlikely that a modest number of randomly selected loci will show significant linkage by chance. One possible exception would be if nonrecombining blocks at the same locus are treated as independent “loci” for the purposes of IMA analyses, as was suggested by Hey and Nielsen (2004) in their initial presentation of the IM methodology as one possible way of dealing with recombination. However, to our knowledge, this approach is not widely used; researchers typically pick a single nonrecombining block from each locus, chosen either randomly or based on size, as we have done here. One might expect that linkage, which would result in correlated histories among loci, would cause artificially narrow confidence intervals around point estimates (Hey and Nielsen 2004), but we do not see evidence of this in our data. This would presumably be more of a concern if a single locus were broken up into multiple nonrecombining loci, which would involve much tighter linkage than did our simulations.

Divergent-selective sweeps are likely to play a role in shaping patterns of gene flow between many recently diverged species. More generally, loci associated with reproductive isolation or species differences will also affect patterns of gene flow and genetic differentiation in genomic regions containing them. Levels of introgression inferred from some moderate number of loci are sometimes interpreted as representing the overall or baseline amount of introgression between species, but in fact, patterns of gene flow and genetic differentiation are expected to vary widely throughout the genome, depending on the number of loci contributing to reproductive isolation or species differences, and their relative strengths (Rieseberg and Burke 2001; Wu 2001; Lexer and Widmer 2008; Strasburg et al. 2009). Various tests based on patterns of sequence variation may be used to infer divergent selection at some loci (e.g., Tajima 1989; McDonald and Kreitman 1991); but in the absence of prior functional data or detailed genomic mapping, it can be difficult to distinguish increased divergence caused by linkage to some factor contributing to reproductive isolation from stochastic variation in the mutational and coalescent processes. An additional way to examine the effects of selection at one or more loci would be to treat the inheritance scalars for each locus as parameters, rather than fixed, identical values as we have done here (Hey and Nielsen 2004), which is possible in the IM and IMA programs. Becquet and Przeworski (2009) attempted to identify loci that had experienced no gene flow in simulated data sets by 1) applying a goodness-of-fit test based on additional data simulated using parameter values sampled from the posterior distributions estimated by IM (as well as a second program, MIMAR); and 2) examining locus-specific gene flow rates estimated by IM. They found the former approach had some power to detect outlier loci, whereas in the latter approach, the outlier loci did not typically show unusually low gene flow rates.

Modest violations of the IM demographic model present relatively few problems, but a potentially more problematic bias can arise if substitution patterns do not match one of the two models available in IMA, HKY and IS. Although the effect of nucleotide substitution model on phylogenetic inference has been a subject of substantial investigation (Felsenstein 1988; Goldman 1993; Felsenstein 2004), it has received considerably less attention in analyses at the level of populations and closely related species. But it is clear that choice of model can have a significant impact on inferences (Palsbøll et al. 2004; Pastene et al. 2007). Here, we found that analyzing HKY-simulated data sets using the IS model and vice versa resulted in relatively small biases. However, when the HKY model is assumed for data simulated under the more complex, and often more realistic, GTR model, there appears to be a consistent downward bias in ancestral N_ef estimates. In addition, variance in parameter estimates among data sets increases, and overall accuracy decreases (fig. 1), with five times as many HPD intervals not containing the true value compared with when the mutation model specified in IMA is correct.

Deviations from the HKY model in the form of among-site rate heterogeneity and rate variation among different transition and transversion classes are likely to be found in many data sets (e.g., Templeton et al. 2000; Whelan et al. 2001). Further investigations into the effects of these substitution model violations on demographic parameter estimation using MCMC methods would be extremely valuable, as would incorporation of more complex nucleotide substitution models into programs that use these methods. Until the effects of more complex substitution patterns are better understood or these models are incorporated into computational methods, researchers would be wise to consider the degree to which their data fit an HKY model when making molecular demographic inferences.

Becquet and Przeworski (2009) found significant increases in the variance of parameter estimates among independent data sets under certain violations of the basic IM model. For the most part, we do not see this pattern, except for data simulated using a GTR substitution model (fig. 1, supplementary file S3, Supplementary Material online). In addition, Becquet and Przeworski (2009) found that model violations tended to lead to poorer convergence properties and increasing multimodality in posterior distributions. We also did not see this pattern, with the exception of divergence-time posteriors for simulations involving gene flow with a third unsampled species. One possible explanation for the differences between our results and those of Becquet and Przeworski (2009) is that their simulations for the most part dealt with different model violations (ancestral population structure, variation in gene flow rate through time) than did ours.

Testing of more complex demographic scenarios indicates that recent population-size changes are likely to introduce a bias in current N_ef estimates (see table 5). However, even our simulated scenarios of instantaneous size change followed by long-term stability or continuous rates of exponential growth throughout the species’ histories are unrealistic for many real-world species pairs. For example, cyclical population-size changes such as those caused by range expansions/contractions associated with climatic cycles have affected many species, especially in temperate regions (Hewitt 2000; Lessa et al. 2003); such episodic patterns of growth can introduce bias into parameter estimates under some circumstances (Adams and Hudson 2004). Likewise, levels of interspecific gene flow are also expected to be episodic in many cases, on both short and long time scales (Gee 2004; Strasburg et al. 2007). Population structure within the ancestral species is another important factor to test, as it may lead to significant overestimation of divergence time (Edwards and Beerli 2000; Wakeley 2000; Arbogast et al. 2002). Becquet and Przeworski (2009) performed some simulations involving ancestral structure and found that it produced an upward bias in ancestral N_ef estimates, perhaps explaining many inferences of surprisingly large ancestral N_ef that have been made using IM and IMa (Becquet and Przeworski 2009 and references therein). Our results indicate that such a bias may also result from linkage among loci or gene flow with a third unsampled species (see fig. 1B). In addition, some empirical studies (e.g., Buhay and Crandall 2005; Strasburg and Rieseberg 2008) report a small ancestral N_ef and significant growth since divergence in at least one descendant species, which may reflect bias caused by some violation of the IM demographic model or nucleotide substitution model (see fig. 1B).

Our five-locus, 80-sequence data sets were sufficient to estimate all parameters with reasonable accuracy under the baseline IM model. However, in most cases, the divergence time posterior probability distribution had nonzero density at the prior upper bound, which was roughly an order of magnitude larger than the true value; and confidence intervals for ancestral N_ef and gene flow were also generally quite large. Additional loci and sequences are expected to improve both the accuracy and the precision of demographic parameter estimates and yield narrower HPD intervals. The ability of IMA and related programs to accurately and precisely estimate the various demographic parameters depends on a number of factors in addition to the number of loci and individuals sampled, including the amount of variation in the loci and the degree of haplotype sharing between species. Further simulations or empirical studies examining the relative benefits of additional loci and/or sequences under various demographic conditions would be extremely valuable (Jennings and Edwards 2005; Felsenstein 2006).

Supplementary Material

Supplementary files S1–S4 are available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).