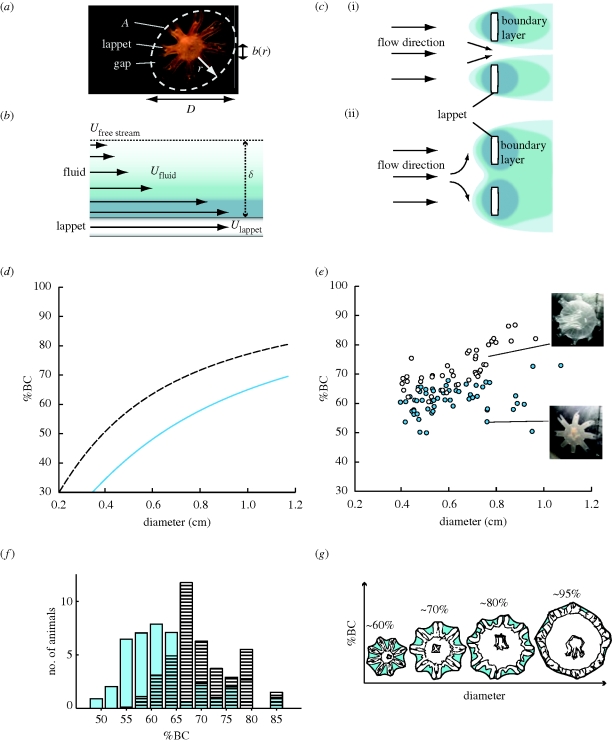
Figure 1.

(a) Characteristic parameters of ephyra morphology. A, potential bell area; D, diameter; r, radial lappet position; b(r), lappet width at radial position r. (b) Model of boundary layer formation on solid surface. U, velocity. Arrows represent velocities relative to free stream flow. Thickness of boundary layer (δ) denotes distance from solid surface to the point where U_fluid = 0.99 × U_{free stream}. (c) Schematic illustration of the two operation modes of the lappet array with different flow Reynolds numbers: (i) filter mode with no boundary layer overlap (high Re); (ii) paddle mode with complete boundary layer overlap (low Re). Different shades of blue correspond to velocity gradient in boundary layer as in (b). (d) Stokes model of bell continuity (BC) as a function of diameter, with C = 0.8. Blue line, model for 13°C; black dashed line, model for 21°C. (e) Morphometric data of Aurelia aurita. BC is plotted against diameter. Blue circles, G₁₃ ephyrae; white circles, G₂₁ ephyrae. Right: two ephyrae from G₂₁ (top) and G₁₃ (bottom) are depicted to illustrate the differences in morphology. (f) Histogram of BC values of the two temperature groups (n = 41 for each group, equal distribution of diameters). Blue bars, G₁₃ ephyrae; black striped bars, G₂₁ ephyrae. (g) Model of continuous boundary layer overlap at all stages of bell development.