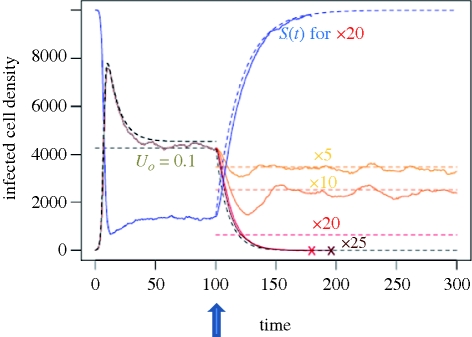
Figure 3.

Effect of a mutagenic treatment on the course of an infection. The dynamics of the infected and susceptible host densities when a mutagen treatment is applied after the start and stabilization of an infection (curative treatment). The treatment consists in an increase in mutation rate relative to the natural rate (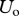 = 0.1, constant mutation model here). The dashed black curve gives the expected dynamics in the absence of mutation (one strain SIS) before the onset of treatment, at t = 100, indicated by the dark blue arrow. From that point each colour corresponds to different mutagen efficiencies (given on the graph). Plain lines give the simulated dynamics at each mutagen efficiency, and dashed lines show the corresponding predicted equilibrium (equation (3.2)): in the absence of extinction, simulated dynamics fluctuate around this prediction. The dashed red curve starting at the onset of the treatment, gives the expected fastest dynamics to extinction (exponential decrease at rate −ν). The dashed blue curve gives the corresponding expected fastest possible increase for S(t), with the plain blue curve giving the corresponding dynamics of S(t) in simulations with a mutagen of effect (×20). The coloured crosses give the time point of extinction in the treatment of the corresponding colour. Mutation effects parameters: shape α = 1.5, mean s̄ = 0.1 with p_L = 20% of true lethals, predicted critical mutagen efficiency is U_c/ ≈ 23 from equation (3.5). Epidemiological parameters: same as figure 2 except λ = 500, and the infection was started at I(0) = 10 and S(0) = S_max = λ/δ.