TABLE 3.

Statistical models describing mutational fitness effects for 77 viable, nonbeneficial, mutations

Model	Probability density functiona	Parameter estimatesb	Log-likelihoodc	Goodness of fitd
Exponential		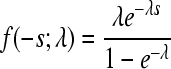λ = 8.144 (6.867;9.564)	35.11	0.957
Gamma		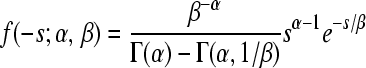α = 0.344 (0.276;0.425)	58.80	0.993
		β = 0.387 (0.262;0.676)
Beta		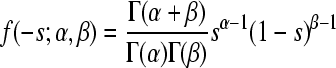α = 0.315 (0.257;0.385)	58.35	0.992
		β = 2.265 (1.661;3.017)
Log-normal		μ = −2.895 (−3.848;−0.916)	60.97	0.994
		σ = 3.473 (2.550;4.691)
Weibull		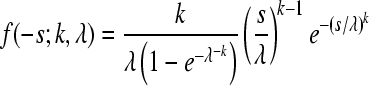λ = 0.079 (0.049;0.161)	60.32	0.994
		k = 0.440 (0.358;0.530)

^aThe constraint 0 ≤ −s ≤ 1 was imposed (0 < −s ≤ 1 for the Log-normal) and probability density functions were normalized accordingly.

^bObtained by maximum likelihood, accounting for experimental error; confidence intervals correspond to an increase of one log-likelihood unit.

^cCalculated from probability densities. Since the latter can be larger than 1, the log-likelihood can be positive.

^dSquared correlation coefficient (r²) between the observed and predicted cumulative distribution functions.