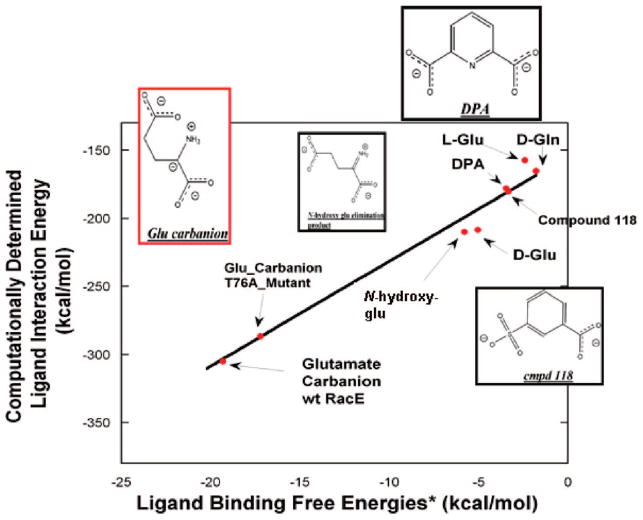
Figure 6.

Experimental binding free energy vs computational interaction energies of glutamate racemase–ligand complexes. Experimental binding energies are all ΔG values, while computational values are ligand–enzyme interaction energies calculated with MMFF94 from energy-minimized structures. The black line is a fit (slope = 7.6 ± 0.5; R = 0.989) to all data. All experimental binding energies were calculated using the standard ΔG = −RT ln(K) relationship. As one cannot directly measure the binding of a transition state/high-energy intermediate by direct binding, one must employ the thermodynamic relationship between the rate of the noncatalyzed reaction vs the rate of the enzyme-catalyzed reaction,⁶⁹ K^‡ = k_non/(k_cat/K_M), where K^‡ is the dissociation constant for the enzyme–transition state complex, k_non is the rate constant for the uncatalyzed reaction (~10⁻¹¹ s⁻¹ for α amino acids⁵²), k_cat is the experimentally determined k_cat, and K_M is the experimentally determined K_M (both k_cat and K_M are taken from the current study). This same procedure is used for both wild-type and T76A RacE. The K_i and IC₅₀ for DPA (2.7 mM) and Compound 118 (2.9 mM), respectively, were taken from the current study. N-Hydroxyglutamate forms an elimination product (structure shown above) upon abstraction of its Cα proton by the Lactobacillus fermenti MurI, with K_i = 54 μM.¹⁴ D-Gln is a weak competitive inhibitor of Aquifex pyrophilus, with K_i = 50 mM.⁴⁷ The K_M values of D- and L-Glu, from the current study, were used to estimate the equilibrium dissociation constants for D- and L-Glu, respectively. A 1 M standard state is used for both the transition-state and inhibitor dissociation constants.