A novel quantitative explanation for the autonomic modulation of cardiac pacemaker cell automaticity via a dynamic system of sarcolemmal and intracellular proteins

Abstract

Classical numerical models have attributed the regulation of normal cardiac automaticity in sinoatrial node cells (SANCs) largely to G protein-coupled receptor (GPCR) modulation of sarcolemmal ion currents. More recent experimental evidence, however, has indicated that GPCR modulation of SANCs automaticity involves spontaneous, rhythmic, local Ca²⁺ releases (LCRs) from the sarcoplasmic reticulum (SR). We explored the GPCR rate modulation of SANCs using a unique and novel numerical model of SANCs in which Ca²⁺-release characteristics are graded by variations in the SR Ca²⁺ pumping capability, mimicking the modulation by phospholamban regulated by cAMP-mediated, PKA-activated signaling. The model faithfully predicted the entire range of physiological chronotropic modulation of SANCs by the activation of β-adrenergic receptors or cholinergic receptors only when experimentally documented changes of sarcolemmal ion channels are combined with a simultaneous increase/decrease in SR Ca²⁺ pumping capability. The novel numerical mechanism of GPCR rate modulation is based on numerous complex synergistic interactions between sarcolemmal and intracellular processes via membrane voltage and Ca²⁺. Major interactions include changes of diastolic Na⁺/Ca²⁺ exchanger current that couple earlier/later diastolic Ca²⁺ releases (predicting the experimentally defined LCR period shift) of increased/decreased amplitude (predicting changes in LCR signal mass, i.e., the product of LCR spatial size, amplitude, and number per cycle) to the diastolic depolarization and ultimately to the spontaneous action potential firing rate. Concomitantly, larger/smaller and more/less frequent activation of L-type Ca²⁺ current shifts the cellular Ca²⁺ balance to support the respective Ca²⁺ cycling changes. In conclusion, our model simulations corroborate recent experimental results in rabbit SANCs pointing to a new paradigm for GPCR heart rate modulation by a complex system of dynamically coupled sarcolemmal and intracellular proteins.

theoretical modeling is an approach to unravel the complexity of cardiac pacemaker function. As early as 1960, a quantitative theory of membrane excitation by Hodgkin and Huxley (H-H) was modified to simulate spontaneous action potentials (APs) of cardiac pacemaker cells (39). Formulation of the 1960 model was a case of “theory leading experiment” (40). Numerous models of the primary cardiac pacemaker cell, the sinoatrial node cell (SANC), have been developed [12 models since 1980 (54)] based on the H-H formalism and extensive studies of sarcolemmal ion currents under voltage clamp. Accordingly, the regulation of the spontaneous SANC rate has been described so far based largely on modulatory changes of ion channels, such as “funny” current (I_f), L-type Ca²⁺ current (I_CaL), steady current (I_st), and acetylcholine-activated K⁺ current (I_KACh) (6, 12, 18, 58). Although the relative contributions of each channel type have been always debated (26, 40, 54), until very recently the dominant point of view was that I_f, sometimes called “the pacemaker current,” provides the major mechanism for heart rate regulation via its voltage activation shifts modulated by cAMP (9, 10). The most recent studies in genetically manipulated mice demonstrated, however, that the β-adrenergic receptor (β-AR) stimulation effect is preserved in the absence of I_f (16) or in the absence of cAMP sensitivity of I_f (1).

Thus, the SANC pacemaker system is likely more complex than just a H-H-type membrane voltage oscillator (i.e., a membrane clock or M clock) and includes additional critical contributions that have not been currently described by the existing numerical models of autonomic modulation of the SANC spontaneous rate (6, 12, 18, 58). Indeed, experimental data of the last two decades have demonstrated that the SANC pacemaker system has a substantial contribution of Ca²⁺ cycling by the sarcoplasmic reticulum (SR) (for reviews, see Refs. 27 and 34). Specifically, confocal imaging detects not only a global intracellular Ca²⁺ transient triggered by the AP but also spontaneous local Ca²⁺ releases (LCRs) from the SR. LCRs emerge beneath the cell membrane as multiple, relatively synchronous, locally propagating Ca²⁺ wavelets later in the cycle, i.e., during the late part of diastolic depolarization (DD) (3, 21). Importantly, the SR behaves as a true intracellular Ca²⁺ oscillator (recently dubbed a “Ca²⁺ clock”), generating rhythmic LCRs observed in voltage-clamped and chemically skinned SANCs (53). Variable periods of the SR Ca²⁺ oscillator are achieved via gradations in basal cAMP-dependent PKA signaling (50) that regulate the SR Ca²⁺ pump (via phospholamban phosphorylation) and likely Ca²⁺-release channels [ryanodine receptors (RyRs)]. LCRs activate the electrogenic operation of the sarcolemmal Na⁺/Ca²⁺ exchanger (NCX), generating an inward current (I_NCX) that imparts a steep, exponentially rising phase to DD (2, 3, 21). Furthermore, robust experimental evidence has indicated that PKA-dependent modulation of LCR characteristics is a major mechanism contributing to the pacemaker rate modulation via β-ARs (rate increase) (2, 49, 50) and cholinergic receptors (ChRs; rate decrease) (32). Specifically, β-ARs or ChRs shorten or prolong the LCR period (time from the peak AP-induced Ca²⁺ transient to the LCR peak), i.e., LCRs occur earlier or later during DD, respectively. Also, the integrated LCR signal or signal mass (the product of LCR size, amplitude, and number per cycle) concomitantly increases or decreases, respectively.

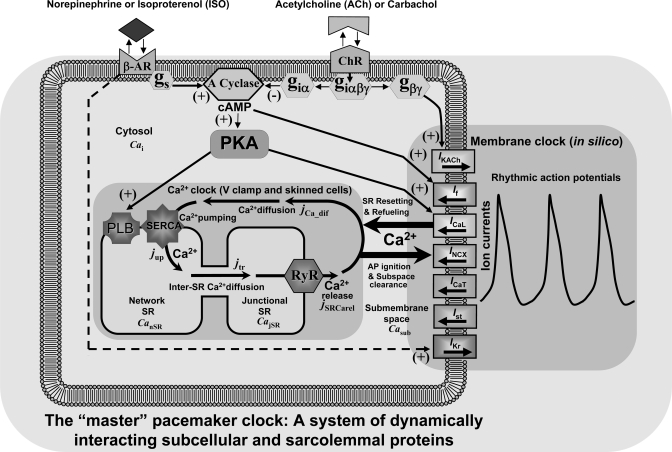
While these results can be interpreted to indicate that G protein-coupled receptor (GPCR) signaling modulates automaticity via the intracellular Ca²⁺ cycling that entrains rhythmic excitations of cell surface membrane (35, 51), the true mechanisms of GPCR modulation are, in fact, likely complex, and exploration of these complex interactions requires numerical modeling. Indeed, surface membrane proteins not only effect changes in membrane potential but also critically regulate intracellular Ca²⁺ cycling [e.g., via effecting the global Ca²⁺ transient, via balancing Ca²⁺ influx and efflux, via AP shape influencing NCX function, etc. (for a review, see Ref. 27)]. In other words, while either clock, by definition, exists without the other only under special experimental conditions (the Ca²⁺ clock under voltage clamp or in skinned cells) or in silico (36, 54), in nature, the clocks' mutual entrainment substantially alters the properties of each clock. Therefore, when operating as a system, the membrane clock and Ca²⁺ clock cease to exist as separate entities: there is only one “master” pacemaker clock (Fig. 1), i.e., a complex oscillatory system of dynamically interacting sarcolemmal and intracellular molecules (27, 36).

Fig. 1.

Schematic illustration of our model of autonomic modulation of a cardiac pacemaker cell system of dynamically interacting subcellular and sarcolemmal proteins. Rate regulation mechanisms were numerically explored for the stimulation of β-adrenergic receptors (β-ARs) or cholinergic receptors (ChRs), to increase or slow rate, respectively. Norepinephrine [or isoproterenol (ISO)] and ACh (or carbachol) bind to their receptors and regulate adenylyl cyclase (A Cyclase) and cAMP levels up and down via their G proteins, G_s and G_iα, respectively. Varying cAMP levels, in turn, via cAMP-dependent PKA phosphorylation of phospholamban (PLB) and L-type Ca²⁺ channels [generating L-type Ca²⁺ current (I_CaL)], couples the function of Ca²⁺ and membrane (M) clocks, resulting in orchestrated and balanced shifts in their function and interactions to robustly control the pacemaker rate. cAMP-dependent “funny” current (I_f) provides a safety mechanism at low rates and rate transitions. In addition, ACh slows the system also via classical ACh-activated K⁺ current (I_KACh) mechanism mediated by G_βγ, an effect that becomes dominant at higher levels (supraphysiological) of [ACh]. I_NCX, Na⁺/Ca²⁺ exchanger current; I_CaT, T-type Ca₂₊ current; I_st, steady current; I_Kr, rapid inward rectifying K⁺ current; SR, sarcoplasmic reticulum; Ca_i, cystolic Ca²⁺; V clamp, voltage clamp; j_{Ca_diff}, the Ca²⁺ diffusion flux from submembrane space to cytosol; SERCA, sarco(endo)plasmic reticulum Ca²⁺-ATPase; j_up, rate of SR Ca²⁺ uptake; j_tr, the Ca²⁺ diffusion flux from the network SR to junctional SR; RyR, ryanodine receptor; j_SRCare1, diastolic Ca²⁺ release; Ca_nSR, Ca_jSR, and Ca_sub, Ca²⁺ in the network SR, junctional SR, and submembrane space, respectively.

We (36) have recently developed a novel unique numerical model of the SANC that features spontaneous diastolic Ca²⁺ releases. Both amplitude (mimicking the LCR signal mass) and phase (mimicking the average LCR period) of Ca²⁺ releases can be graded in the model by gradations in the SR Ca²⁺ pumping capability, mimicking experimentally defined changes in phospholamban function resulting from gradations in phospholamban phosphorylation by the cAMP-mediated activation of PKA. The present study uses this model to explore a novel quantitative explanation for the autonomic modulation of the spontaneous AP rate of SANCs via β-AR and ChR stimulation.

METHODS

Numerical SANC Model

The present study is based on our recently published “basal state firing model” of rabbit SANCs (36). This numerical model can be downloaded and run in CellML format (http://models.cellml.org/workspace/maltsev_2009). The formulations of the original model (36) were upgraded (Fig. 1) to simulate the effects of stimulation of β-ARs and ChRs as described below. All model details, including mathematical formulations and specific parameter values, are provided in the Supplemental Material.¹ All 30 model variables and their initial values are listed in Supplemental Table S1.

Simulation of I_CaL in the Basal State

I_CaL is a major player in our model: it 1) generates the AP upstroke; 2) contributes to late DD; 3) “resets” Ca²⁺ cycling by triggering global Ca²⁺-induced Ca²⁺ release, resulting in strong SR Ca²⁺ depletion (36); and 4) “refuels” the SR by supplying (each cycle) SANCs with Ca²⁺ to be pumped into the SR (36). We used standard formulations for I_CaL described by activation and inactivation gating (variables d_L and f_L) and Ca²⁺-dependent inactivation (f_Ca) as previously described (24). A critical parameter determining the I_CaL contribution to DD is its activation threshold, and, therefore, this parameter was carefully considered in our model. The activation threshold has been measured in several patch-clamp studies of isolated rabbit SANCs and was found to be “positive to −45 to −50 mV” (8), “around −60 mV” (48), “between −50 and −40 mV” (38), or “approximately −40 mV” (52). A relatively low activation threshold of I_CaL in SANCs might be explained, at least in part, by two factors: 1) L-type Ca²⁺ channels could be phosphorylated by PKA, which is highly active in the basal state (43, 50); and 2) I_CaL in SANCs might be a combination of Ca_v1.2 and Ca_v1.3, as shown in mouse SANCs (37). Accordingly, we assigned the midpoint of the I_CaL steady-state activation curve (36) to −13.5 mV, to be in line with the aforementioned experimental data on the I_CaL activation threshold in rabbit SANCs (see Supplemental Table S2 for a comparison with different SANC models). With our settings, the magnitude of the simulated I_CaL peak induced by a voltage step to −60 mV (from −80 mV) is negligible (<1 pA), but the actual I_CaL activation begins at about −50 mV (3.17 pA or 0.1 pA/pF) and increases to 13.7 pA (0.43 pA/pF) at −40 mV (see the full current-voltage curve in Supplemental Fig. S1). During simulated AP firing, the I_CaL magnitude increases from 2.24 pA (0.07 pA/pF) to 8.87 pA (0.277 pA/pF) as DD progresses from −50 to −40 mV (Supplemental Fig. S2).

Specific Formulations for the Modulation of Ca²⁺ Cycling and Ion Channels by ACh

We included formulations for I_KACh that were previously suggested by Demir et al. (6):

$$I_{\text{KACh}}=a\times g_{\text{KACh,max}}\times (V_{\text{m}}-E_{\text{K}})$$ (1)

where E_K is the K⁺ equilibrium potential, g_KACh,max is the maximal conductance of I_KACh, and V_m is membrane voltage. The gating variable a(V_m, [ACh], t; where t is time) in this model is governed by an opening rate constant (β) that is [ACh] dependent and a closing rate constant (α) that is voltage dependent:

$$\beta =0.01232/(1+0.0042/[\text{ACh}])$$

$$\alpha =0.017\times \exp [0.0133(V_{\text{m}}+40)]$$

$$\text{d}a/\text{d}t=\beta (1-a)-\alpha \times a$$

where β and α are given in 1/ms, [ACh] in mM and V_m in mV. Modulation of I_f and I_CaL by ACh is formulated in the present study as suggested in the 2002 Zhang et al. model (58). In short, the shift (s; in mV) of the I_f activation curve by ChR stimulation is described by the following Michaelis-Menton-type equation:

$$s=s_{\max }{[\text{ACh}]}^{n_f}/\left(K_{0.5,f}^{n_f}+{[\text{ACh}]}^{n_f}\right)$$ (2)

where s_max = −7.2 mV is the maximum shift of the I_f activation curve, n_f = 0.69 is the Hill coefficient, and K_0.5,f = 12.6 nM is the ACh concentration that produces half-maximal shift of the I_f activation curve. The fractional block (b_CaL) of I_CaL conductance (g_CaL) by ChR stimulation is also calculated using the following Michaelis-Menton-type equation:

$$b_{\text{CaL}}=b_{\text{CaL,max}}\times [\text{ACh}]/(K_{0.5,\text{CaL}}+[\text{ACh}])$$ (3)

where K_0.5,CaL = 90 nM. As to the range of I_CaL modulation, the experimental data greatly vary: from very strong inhibition by 56%, as reported by Petit-Jacques et al. (43), to no effect, as reported at least in two studies (20, 42). Avoiding the extremes, we assigned a moderate maximum inhibition of I_CaL to 31% (b_CaL,max = 0.31) based on an experimental report by Zaza et al. (56).

Our model adopts formulations of Luo and Rudy (30) for the rate of SR Ca²⁺ uptake (i.e., pumping), j_up, in the form of the following simple Michaelis-Menton-type function of cytosolic [Ca] (Ca_i):

$$j_{\text{up}}=P_{\text{up}}/(1+K_{\text{up}}/{\text{Ca}}_{\text{i}})$$ (4)

where P_up is a maximum uptake rate, i.e., the capability of the SR to pump Ca²⁺ (at a given state of phospholamban phosphorylation), and K_up is the Ca_i sensitivity of the SR Ca²⁺ pump. A major new feature of the present model is that we introduced a dependence of P_up on ChR stimulation, mimicking the effect phospholamban dephosphorylation by ChR activation in rabbit SANCs (32):

$$P_{\text{up}}=P_{\text{up,basal}}\times (1-b_{\text{up}})$$ (5)

where P_up,basal is P_up in the basal state [P_up,basal = 12 mM/s, as in our original “basal state” model (36)] and b_up is the fractional block of SR Ca²⁺ pumping due to phospholamban dephosphorylation. Since PKA simultaneously regulates both phospholamban and L-type Ca²⁺ channels, we assumed that the inhibition of SR Ca²⁺ pumping capability by ChR stimulation closely follows the established relationship of the inhibition of I_CaL (Eq. 3) (58):

$$b_{\text{up}}=b_{\text{up,max}}\times [\text{ACh}]/(K_{\text{0.5,up}}+[\text{ACh}])$$ (6)

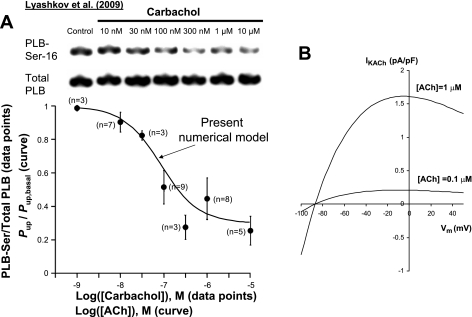
where K_0.5,up = K_0.5,CaL = 90 nM is the [ACh] for half-maximal inhibition and b_up,max = 0.7. The resultant relative decrease of P_up [i.e., P_up ([ACh])/P_up,basal] shown by the solid curve in Fig. 4A (see results for details) closely fits the dose-response relationship of the dephosphorylation of phospholamban at Ser¹⁶ previously experimentally measured in rabbit SANCs at graded levels of ChR stimulation (32).

Fig. 4.

A: the modeled relative decrease of the capability of SR Ca²⁺ pumping, P_up (“Present numerical model” curve) closely fits the relation of PLB dephosphorylation at Ser¹⁶ previously experimentally measured in rabbit SANCs at graded levels of ChR stimulation. The curve was calculated as follows: P_up/P_up,basal = 1 − b_up([ACh]), where b_up is defined according Eq. 6. B: model characterization of I_KACh at two ACh concentrations, using the classical I_KACh formulation by Demir et al. 1999 (6). I_KACh exhibits only a relatively small activation at 100 nM ACh. [All experimental data in A are reproduced from Ref. 32.]

Model Parameters in Simulations of the Effect of β-AR Stimulation

The key membrane parameters were changed in accordance with experimentally documented changes induced by β-AR stimulation by isoproterenol (see details in Supplemental Table 3). Specifically, g_CaL was increased by 75% (49). We did not shift the midpoint of the I_CaL steady-state activation curve in our simulations of β-AR stimulation because the threshold of I_CaL activation remained unchanged in rabbit SANCs after the application of isoproterenol in a thorough experimental study by Zaza et al. (56). The activation curve for I_f was shifted by 7.8 mV toward positive potentials (10). We increased the maximum conductance (g_Kr) for the rapid delayed rectifying K⁺ current (I_Kr) by 50% because isoproterenol reportedly increases K⁺ current in rabbit SANCs (29) [although likely via a PKC-dependent mechanism (15)]. In addition to changes of membrane conductances, we also changed the capability of SR Ca²⁺ pumping, P_up [mimicking the effect of the increased phospholamban phosphorylation (50)]. Since isoproterenol-induced changes of P_up are unknown, we performed a parametric sensitivity analysis for this parameter.

Numerical Integration

Source code for the model was developed using Borland Delphi-7 software. Model integration was performed on a Pentium 4 (2.8 GHz)-based PC with a fixed time step of 0.01 ms.

Steady-State Solutions

We followed the algorithm previously suggested by Kurata et al. (25): numerical integration was continued until the relative differences in both amplitude and period between the newly calculated cycle and the preceding cycle became <0.001.

RESULTS

Prediction of β-AR Stimulation

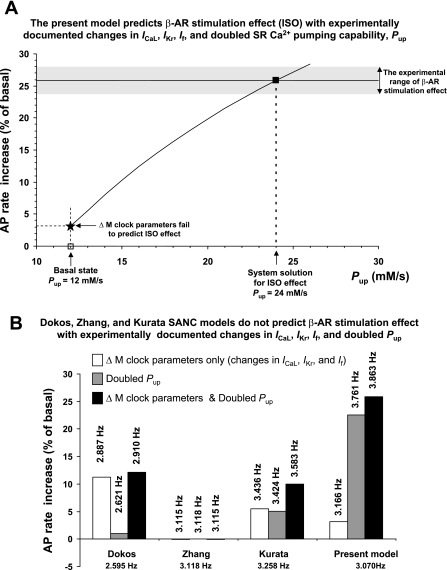
Supplemental Table S3 (“Primary model set”) shows specific parameter changes and numerical results (absolute and relative rate changes) of our simulations of β-AR stimulation. Surprisingly, substantial simultaneous changes of all three major membrane clock components (I_CaL, I_f, and I_Kr) produced only a moderate 3.15% increase of the AP firing rate (solid star in Fig. 2A) in our modelled SANC system when the capability of SR Ca²⁺ pumping remained at its basal state of 12 mM/s (left vertical arrow in Fig. 2A). This was far below the β-AR stimulation-induced effect that has been experimentally documented in rabbit SANCs, within 23.7% (49) to ∼28% (14), as marked by the shaded band in Fig. 2A.

Fig. 2.

Present numerical model solution (■ in A) for the SR Ca²⁺ pumping capability (P_up) to experimentally predict the documented range of β-AR stimulation on the action potential (AP) firing rate (14, 49) (shown by the shaded band). In contrast, previous SANC models, lacking diastolic Ca²⁺ release, do not predict experimental results (B). Models are labeled as follows: “Dokos”(11), “Zhang” (57), and “Kurata”(24). Respective bars show the effects of changes of M clock parameters, doubling P_up, or both changes combined. M clock changes included a 75% increase of I_CaL conductance (g_CaL) (49), a 7.8-mV shift of the activation curve for I_f (10), and a 50% increase of I_Kr conductance (g_Kr) (29). See Supplemental Table S3 for more details. The spontaneous rate change was negligible (within 0.1%) in the Zhang et al. model (note that this model has no Ca²⁺ dynamics, i.e., [Ca²⁺] = constant). Absolute AP firing rates predicted by the models are shown by the numbers above the respective bars.

Our previous experimental study (50) showed that β-AR stimulation greatly (by a factor of 2.4) increases phospholamban phosphorylation, resulting in an expected increase in P_up. However, the P_up value cannot be directly measured in SANCs and remains unknown. Since previous studies have also shown that Ca²⁺ releases from the SR critically contribute to β-AR stimulation (49, 50) and that these releases are controlled by SR Ca²⁺ pumping (50), we tested the hypothesis that graded increases in P_up (solid curve in Fig. 2A), in addition to the aforementioned major ion current changes, would provide a reasonable numerical solution for experimental results with β-AR stimulation. Indeed, a 25.8% rate increase (marked by the solid square in Fig. 2A, i.e., close to the middle of the experimental range) was achieved in the model, with P_up doubling from 12 to 24 mM/s.

We compared our model predictions for β-AR stimulation with those of some previous rabbit SANC models in response to similar changes of their parameters (Fig. 2B). The combined effect of the same relative changes in conductances for I_CaL and I_Kr and the same shift of I_f activation resulted in a moderate rate change in both the Dokos et al. model [Dokos model (11)] and Kurata et al. model [Kurata model (24)], a result that was similar to our model. Curiously, simulations of 2000 Zhang et al. model of central SANCs [Zhang model (57)] was not sensitive to the combined changes (note that in this particular model intracellular [Ca²⁺] was originally set to a constant).

In contrast to previous models, our model is highly sensitive to the SR Ca²⁺ pumping rate (shaded bars in Fig. 2B); doubling P_up, per se, produced a 22.5% rate increase, providing the major contribution to the β-AR stimulation effect. While the Dokos and Kurata models include formulations for Ca²⁺ dynamics, they do not have terms for diastolic Ca²⁺ release, and doubling P_up produces a mere 1% and 5% rate increase, respectively (shaded bars in Fig. 2B). Therefore, none of the tested classical models provides a solution for the effect of β-AR stimulation, either with experimentally documented changes in major sarcolemmal ion channels (open bars in Fig. 2B) or with these changes combined with a doubled capability of SR Ca²⁺ pumping (solid bars in Fig. 2B).

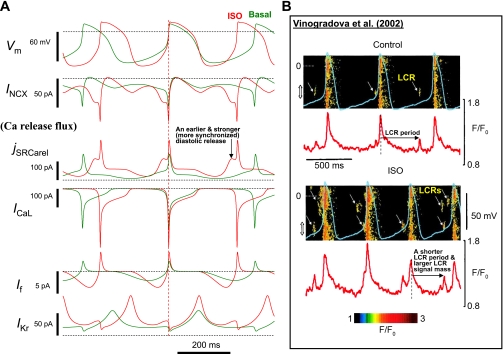
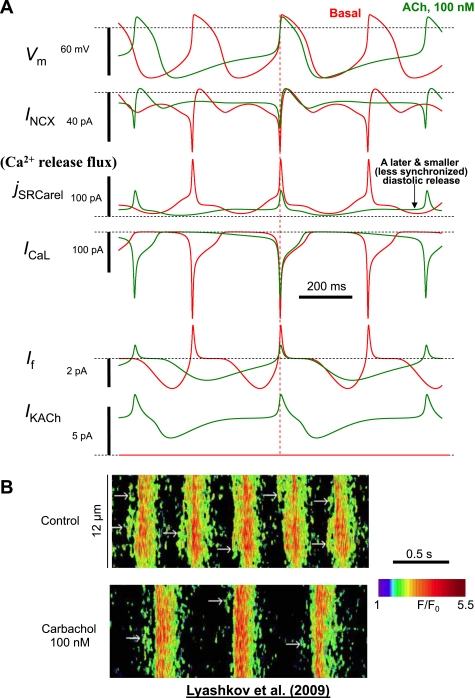
Our numerical mechanism of β-AR stimulation is demonstrated in Fig. 3A, which shows simulated dynamics of major components of the system. In addition to the well-known and expected increases in the amplitudes of ion channel currents (I_CaL, I_f, and I_Kr), diastolic I_NCX activation occured earlier in the cycle and doubled in amplitude, due to the earlier occurrence and concomitant strong increase of diastolic Ca²⁺ release (j_SRCarel), respectively. The earlier occurrence of the diastolic Ca²⁺ release in our model (j_SRCarel panel in Fig. 3A) reproduced the documented isoproterenol-induced shortening of the LCR period (50) (horizontal arrows in Fig. 3B). In turn, the stronger diastolic Ca²⁺ release reproduced the documented isoproterenol-induced increase in LCR signal mass, i.e., the product of LCR spatial size, amplitude, and number per cycle (49) (more frequent and larger-sized LCRs; Fig. 3B).

Fig. 3.

A: simulations showing the novel mechanism of β-AR stimulation to integrate the function of system components. While the major immediate mechanism of cycle length reduction is an earlier and stronger I_NCX, the stronger and more frequent I_CaL critically supports this I_NCX function by supplying more Ca²⁺ to the cell and thereby enhancing SR function. Simulated traces are synchronized at the phase of membrane potential (V_m) = 0 (vertical dashed line) to show the earlier and stronger activation of diastolic Ca²⁺ release (j_SRCarel) and I_NCX, resulting in the earlier and stronger diastolic depolarization(DD) acceleration. B: an example experiment, in which submembrane Ca²⁺ signals by confocal microscopy and V_m by perforated patch clamp were recorded in rabbit sinoatrial node cells (SANCs) in control and after stimulation of β-AR with ISO. Diastolic local Ca²⁺ releases (LCRs) are shown by yellow arrows. ISO increases the LCR signal mass and shifts the LCR occurrence to earlier times within the spontaneous cycle. Red curves (below the confocal images) show the time course of spatial averages calculated within the location marked by double-headed arrows along the scanning lines. This important effect is predicted by our model (see the Ca²⁺ release flux in A, solid vertical arrow). [Images and time series in B were reproduced for illustration from Vinogradova et al. (49) and modified by adding LCR labels and the arrows showing the LCR periods, respectively.]

We also simulated changes in the current-voltage curve for peak I_CaL and in subthreshold I_CaL dynamics during mid-DD (Supplemental Figs. S1 and S2) and found that I_CaL becomes activated earlier and to a greater extent during β-AR stimulation. Interestingly, this apparent I_CaL activation shift was linked to a larger g_CaL but not to intrinsic activation gating (because the midpoint of the I_CaL steady-state activation curve remained unchanged in our simulations; see methods). While the subthreshold I_CaL increased during β-AR stimulation, it was still much smaller than I_NCX during the entire DD, e.g., 3.1 vs. 39 pA at −50 mV and 11.8 vs. 40.9 pA at −40 mV; I_CaL and I_NCX became equal (−44.4 pA) only at −29 mV, i.e., above the I_CaL threshold. It is also important to note that Ca²⁺- and voltage-dependent responses to β-AR stimulation were well balanced within the system: increased Ca²⁺ influx via increased and more frequent I_CaL supported larger SR Ca²⁺ releases and greater Ca²⁺ efflux via the doubled I_NCX.

Prediction of ChR Stimulation

Previous experimental results (32, 47) have shown that the mechanism of SANC rate slowing via ChR activation is complex and includes changes in both sarcolemmal ion currents and diastolic Ca²⁺ release. Electrophysiological changes include PKA-dependent I_CaL reduction (43, 56), a shift of cAMP-dependent I_f activation toward negative potentials (9, 10), and G_i-dependent activation of I_KACh (6, 12) (Fig. 1). The change in diastolic Ca²⁺ release is mediated, at least in part, by a reduction in cAMP-dependent PKA signaling, resulting in phospholamban dephosphorylation (32), which is expected to decrease the capability of SR Ca²⁺ pumping (Eqs. 4 –6).

In the rabbit sinoatrial node, ACh application of up to 100 nM decreases the AP rate by up to ∼50%, an effect generally considered as physiological rate regulation (58). Since carbachol, a ChR agonist, decreases the AP rate by ∼50% in rabbit SANCs also at 100 nM (32), its efficacy to stimulate ChRs must be similar to that of ACh, and, therefore, (Eqs. 5 and (6 reasonably describe P_up inhibition at various [ACh] (solid curve in Fig. 4A) based on experimental data of phospholamban dephosphorylation at various carbachol concentrations (data points in Fig. 4A). In line with these experimental results, our model predicted an approximate half-maximal effect (52.6%) of SR Ca²⁺ pump inhibition at 100 nM [ACh], i.e., a 36.8% in P_up, which is a decrease from its basal state value of 12 to 7.58 mM/s.

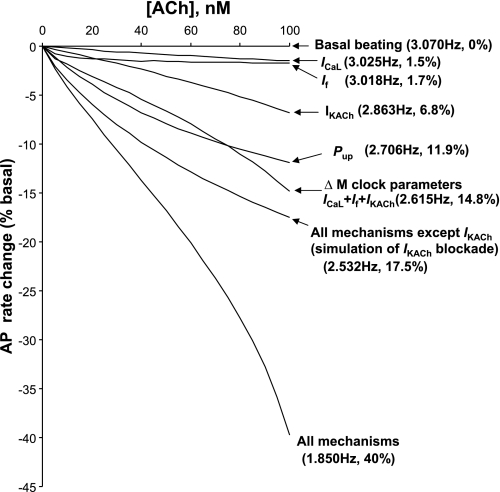
Next, we tested the effects and interactions of all four aforementioned ACh-dependent mechanisms (P_up, I_CaL, I_f, and I_KACh) to reduce the AP firing rate in the model in response to ACh within this moderate concentration range (up to 100 nM; Fig. 5; see Supplemental Table 4 for specific model parameters to simulate the effect of ChR stimulation). The model predicted that the basal beating rate substantially reduced by 40% from its basal value (“All mechanisms” curve in Fig. 5), in line with experimental observations of a 50% rate reduction in rabbit SANCs (32). Our simulations showed that the beating rate reduction includes two major mechanisms that act on membrane potential: 1) changes in I_NCX due to changes in SR Ca²⁺ cycling and 2) activation of I_KACh due to G_i signaling (Figs. 1 and 6A).

Fig. 5.

Synergism of different component mechanisms in moderate SANC rate slowing by [ACh]. Results of model predictions for spontaneous AP rate reduction at various moderate ACh concentrations (up to 100 nM) for different mechanisms (as shown). Modulation (inhibition) of the capability of SR Ca²⁺ pumping by ACh was described by Eqs. 5 and 6.

Fig. 6.

A: simulations of the present model showing the new mechanism of the ChR stimulation effect that integrates function of components of the Ca²⁺ clock and M clock. While the major immediate mechanism of the cycle length increase is a later and smaller I_NCX, the smaller and less frequent I_CaL critically supports this I_NCX function by supplying less Ca²⁺ to the cell and thereby decelerating SR function. Simulated traces are synchronized at the phase of V_m = 0 (vertical dashed line) to show the later and smaller activation of j_SRCarel and I_NCX. B: an example of recording of Ca_sub signals by confocal microscopy in rabbit SANCs in control and after stimulation of ChR with carbachol (100 nM). Carbachol decreased the LCR signal mass and shifted the LCR occurrence to later times within the spontaneous cycle. This important effect is predicted by our model (see Ca²⁺ release flux in A). [Images in B were reproduced for illustration from our recent study (32).]

The later occurrence of diastolic Ca²⁺ release in the model simulations reproduced the experimentally documented increase of the LCR period affected by ChR stimulation (Fig. 6B) (32). In turn, the smaller diastolic Ca²⁺ release reproduced the experimentally documented decrease in LCR signal mass (the product of LCR spatial size, amplitude, and number per cycle; Fig. 6B) (32). In turn, a reduction of Ca²⁺ influx in the model via smaller and less frequent I_CaL came into balance with the smaller Ca²⁺ releases and reduced Ca²⁺ efflux via the substantially decreased I_NCX.

A major contribution of I_KACh in the physiological chronotropic effect of ACh at 100 nM (Figs. 5 and 6A) is not surprising. The classical ACh-activated mechanism has been previously well characterized, both experimentally and theoretically (see, e.g., Refs. 6, 32, and 58), and, therefore, it was not explored here in detail. Rather, we simulated the effect of ACh in the presence of I_KACh blockade (“All mechanisms except I_KACh” curve in Fig. 5). At 100 nM ACh, the effect reached about one-half of the total effect, 17.5% vs. 40%, i.e., consistent with experimental data (32) (see more in the discussion).

This moderate ACh concentration of 100 nM 1) activated only ∼13% of I_KACh observed at 1 μM ACh (Fig. 4B, according to Eq. 1); 2) reduced I_CaL by 16.3% (Supplemental Fig. S1, about one-half of its maximum modulation range of 31%, see Eq. 3); 3) shifted I_f activation nearly maximally (activation was shifted by −5.8 mV of the maximum shift of −7.2 mV, see Eq. 2); and 4) reduced P_up from 12 to 7.58 mM/s (Eqs. 5 and 6).

Importantly, the model predicted a relatively small (compared with 40%) reduction of the beating rate produced by each separate mechanism alone at 100 nM ACh (shown by arrows in Fig. 5): I_CaL, 1.5%; I_f, 1.7%, I_KACh, 6.8%, and P_up, 11.9%, reflecting a synergism in their combined effects (40%) to slow the rate of the SANC system. Furthermore, changes in membrane ion channels alone (I_CaL + I_f + I_KACh) slowed the rate by 14.8%, reflecting a synergism of membrane mechanisms (1.5 + 1.7 + 6.8 = 10 << 14.8) as well as a synergism between the membrane mechanisms and SR Ca²⁺ cycling (14.8 + 11.9 = 26.7 << 40). Thus, effective (physiological) rate reduction by 40% was achieved in the model via relatively small but synergistic changes of all ACh-dependent system components.

Detailed Numerical Analysis of How β-AR and ChR Stimulation Modulate Spontaneous SR Ca²⁺ Release in the Submembrane Compartment

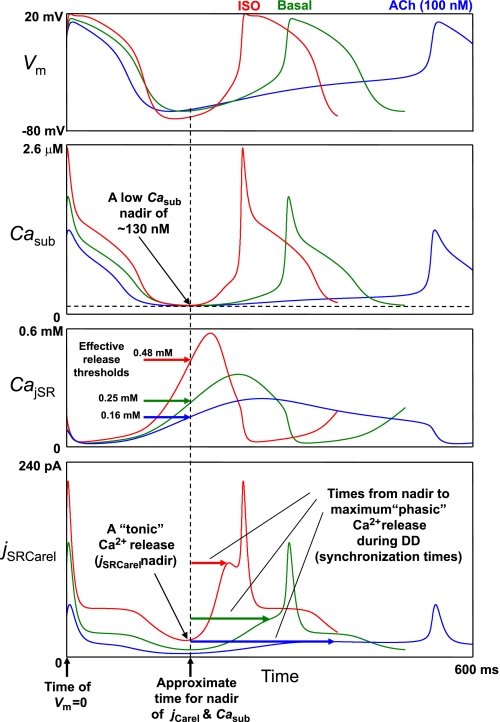
Our mathematical formulation of SR Ca²⁺ release (j_SRCarel) by RyRs in rabbit cardiac cells was adopted from Stern et al. (46) and Shannon et al. (45) (see the Supplemental Material for details). j_SRCarel dynamics are governed by the difference between [Ca²⁺] in the junctional SR and [Ca²⁺] in the submembrane space (i.e., Ca_jSR − Ca_sub) and by a gating variable [O(t)] describing the transition of RyRs to the open state: j_SRCarel = k_s × O × (Ca_jSR − Ca_sub), where k_s is a constant (the maximum Ca²⁺ release flux). In turn, the O(t) rate is increased as a nonlinear function of intra-SR [Ca²⁺] (Ca_jSR) and extra-SR [Ca²⁺] (Ca_sub). Figure 7 shows simulations of simultaneous changes of V_m (to assess the DD phase), Ca_sub, Ca_jSR, and j_SRCarel for basal beating (“Basal” traces), β-AR stimulation (“ISO” traces), and ChR stimulation with 100 nM ACh (“ACh” traces). The results of the analysis of the interplay of these factors to activate the diastolic release are as follows.

Fig. 7.

Model prediction for the mechanisms of spontaneous Ca²⁺ release in rabbit SANCs and their modulation by β-AR or ChR stimulation. Shown are model simulations of the simultaneous changes in V_m, Ca_sub, Ca_jSR, and Ca²⁺-release flux (j_SRCarel). While the increase in diastolic Ca²⁺ release is initiated by a rising Ca_jSR, a subsequent strong increase in Ca²⁺ release and local (within the submembrane space) Ca²⁺-release synchronization are due an increasing Ca_sub (i.e., Ca²⁺-induced Ca²⁺ release).

Item 1.

During very early DD, the Ca²⁺ transient in the submembrane space is decaying (Ca_sub), but SR loading is increasing in all three cases. Thus, Ca_sub decay “pushes” j_SRCarel down, but rising Ca_jSR “pushes” it up. Since Ca_sub decay dominates on its effect on j_SRCarel, the release flux is decaying simultaneously with the Ca_sub decay.

Item 2.

The decaying Ca_sub and j_SRCarel reach their nadir at approximately the same time (vertical dashed line in Fig. 7). The nadir for Ca_sub is at about the same relatively low level of ∼130 nM (horizontal dashed line in Fig. 7). An interesting model prediction is that the nadir for j_SRCarel is not negligible and becomes especially noticeable in the case of isoproterenol treatement [consistent with experimental results demonstrating that early DD is also accelerated by the Ca²⁺ release during β-AR stimulation (2)]. In other words, the predicted diastolic release has two components: a smaller “persistent” or “tonic” component (evident at the j_SRCarel nadir) and a larger “phasic” (i.e., increasing) component, as described below.

Item 3.

Once Ca_sub decay is complete, rising Ca_jSR becomes dominating in its effect on j_SRCarel. Thus, the next important model prediction is that the initial, “phasic” diastolic spontaneous Ca²⁺ release (i.e., Ca²⁺ release increase) is triggered/governed by the increasing Ca_jSR (i.e., SR Ca²⁺ load).

Item 4.

While we did not change intrinsic RyR release activation by intra-SR Ca²⁺ (parameter EC_{50_SR}; see the Supplemental Material for details), the effective release threshold (release begins to increase) is higher for isoproterenol treatment but lower for ACh treatment. This happens because during about the same period of time (before the release nadir, marked by vertical dashed line in Fig. 7) a higher rate of SR refilling with Ca²⁺ brings Ca_jSR to a higher level (solid horizontal arrows in Ca_jSR panel in Fig. 7). Of note, the effective Ca²⁺ release threshold is lower than the peak of Ca_jSR (i.e., an “apparent” threshold) because when Ca²⁺ release is activated, its initial amplitude is relatively small not sufficient to deplete the SR; the Ca²⁺ level in the SR, in fact, still continues to increase until the release flux and refilling flux equilibrate (at the Ca_jSR peak).

Item 5.

Diastolic Ca²⁺ release is more synchronized in the case of isoproterenol treatment (more Ca²⁺ is released per unit time; see the j_SRCarel panels in Figs. 3A and 7) but is less synchronized (rising very slowly) in the case of ACh treatment (Figs. 6A and 7). The more release synchronization in the case of isoproterenol is due to a stronger increase in Ca_sub (Ca_jSR is declining during this phase). Thus, while the diastolic release increase is initiated by an increase in Ca_jSR (i.e., by SR Ca²⁺ refilling; see item 3), the subsequent and greater increase and synchronization of Ca²⁺ release is due to a rising Ca_sub (i.e., a secondary release, or Ca²⁺-induced Ca²⁺ release). An important consequence of the increased synchronization of release is that the release flux achieves a larger amplitude in a shorter time in the case of isoproterenol (i.e., time from the j_SRCarel nadir to its maximum, shown by the horizontal arrows in the j_SRCarel panel in Fig. 7). Conversely, in the case of ACh treatment, less synchronization of diastolic release results in a smaller release amplitude achieved at a longer time (see the discussion for details).

Item 6.

While the grater increase in Ca_sub during DD is mainly contributed by the SR Ca²⁺ release into a small volume of submembrane space, it is also contributed (albeit to a lesser degree) by a small Ca²⁺ influx via subthreshold I_CaL activation. During basal state beating, the subthreshold I_CaL reaches its maximum of 8.87 pA at −40 mV (see Supplemental Fig. S2), i.e., only ∼19% of the Ca²⁺-release current (i.e., trans-SR Ca²⁺ current) at this voltage during DD (45.8 pA; Fig. 3A). In the case of isoproterenol treatment, the relative I_CaL contribution becomes smaller (11.8 vs. 115.4 pA, i.e., ∼10%; Fig. 3A). However, in the case of ACh treatment, the predicted relative I_CaL contribution substantially increases and becomes comparable with that of j_SRCarel (8 vs. 19.1 pA, i.e., ∼42%; Fig. 6A).

Simulation of GPCR Modulation in Cells With Different Basal Parameters

Since the model predictions are sensitive to the input parameters, we tested and confirmed the robustness of our finding of the diastolic Ca²⁺ release importance in GPCR modulation in two additional simulation series. In these two basal model settings, two major sarcolemmal conductances (g_CaL,max and g_If,max, for I_CaL and I_f) were substantially increased (“More I_f and I_CaL” model set) or decreased (“Less I_f and I_CaL” model set) by 25% versus their original values in our primary model [note that the simulated I_CaL and I_f of these two sets were still within experimental range reported by Honjo et al. (19); not shown]. We performed parameter sensitivity analysis to find solutions for the experimental β-AR stimulation effect and also to predict ACh modulation within 0–100 nM (see results in Supplemental Tables 3 and 4). In both additional model parameter sets, the rate regulation via only membrane clock parameter changes was ineffective and substantially less than that when changes in SR Ca²⁺ cycling were added (i.e., via all mechanisms). In the case of β-AR stimulation, additional changes in P_up were required to reach the experimentally documented 25.8% rate increase. Interestingly, AP firing ceased in simulations with the “Less I_f and I_CaL” model set when [ACh] increased above 43 nM, indicating that I_CaL and I_f are important fail-safe mechanisms for SANC automaticity at higher [ACh] (see the discussion for details).

DISCUSSION

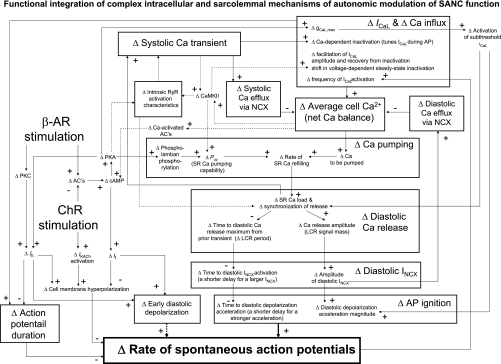
While all prior SANC models (12 models since 1980, according to Ref. 54) have been mainly based on a H-H-type membrane voltage oscillator, the present numerical study revealed that the rate of spontaneous APs in cardiac pacemaker cells is modulated by GPCR signaling via a complex dynamic integration of voltage- and Ca²⁺-dependent processes within the SANC system (Fig. 8), consistent with experimental results (32, 47, 49, 50, 55) and recent reviews (27, 34). The shifts (marked by Δ) in the balance of system components (which ultimately determine the chronotropic response) are looped and are thus interdependent. In such a complex system, there are no “simple” reactions to GPCR signaling, like a simple activation of “the pacemaker channel” (10) or simple NCX activation by a “Ca²⁺ oscillator” or “Ca²⁺ clock” (35, 51). All perturbations, in fact, change the system balance (e.g., cell Ca²⁺ balance or steady-state DD/AP shape) that directly or indirectly affect all system components. The effective modulation of such a complex system cannot be achieved by perturbing just a single system component (the robust system with redundant mechanisms may compensate the change) but rather requires a modulation of system nodes to orchestrate simultaneous unidirectional shifts in numerous system elements to achieve a true higher (or lower) system balance (rather than a compensatory reaction), as described below.

Fig. 8.

Schematical illustration of our hypothesis of how autonomic modulation impacts on functional integration of numerous interdependent intracellular and sarcolemmal mechanisms to effect changes in the spontaneous AP firing rate. The hypothesis is based on available data in the literature and the numerical modeling of the present study. See the discussion for details.

A Novel Pacemaker Rate Regulation Paradigm via Coupling Factors

A recent experimental study (50) in rabbit SANCs discovered that phospholamban is strongly phosphorylated in the basal state, thus providing a new rate regulation mechanism: gradations in the SR Ca²⁺ pumping rate that result in gradations of LCR characteristics. The physiological rate increase by the activation of β-ARs is linked to a greater extent of phospholamban phosphorylation (50) resulting in earlier, more frequent, and larger diastolic Ca²⁺ releases (Figs. 3B and 8). In contrast, the physiological rate decrease by the activation of ChRs is linked to phospholamban dephosphorylation (Fig. 4A), resulting in later, less frequent, and smaller diastolic releases (Figs. 6B and 8) (32). In our basal state model, the capability of SR Ca²⁺ pumping, P_up, is relatively high [12 vs. 5 mM/s in the Kurata model (24)], simulating experimentally documented basal phospholamban phosphorylation that was not considered in Kurata model. Various degrees of P_up in our model (mimicking the regulatory function of phospholamban) modulate the AP firing rate by coordinated changes of the diastolic Ca²⁺ release phase and amplitude, which, in turn, modulate late diastolic I_NCX, in line with aforementioned data in rabbit SANCs (Figs. 3, 6, and 8).

According to our hypothesis (Fig. 8), the SANC AP firing rate is regulated by “enzymatic” coupling factors (36), such as cAMP-mediated, PKA-dependent, and calmodulin kinase II (CaMKII)-dependent protein phosphorylation and by Ca²⁺, per se, that simultaneously influence voltage- and Ca²⁺-dependent mechanisms via the following sequence of events: modulation of I_CaL and P_up (and also likely RyR activation characteristics; see dashed lines in Fig. 8) by PKA and CaMKII activation via protein phosphorylation → diastolic Ca²⁺ release phase and amplitude → I_NCX phase and amplitude → DD acceleration phase and magnitude → AP rate (see results and Fig. 8 for details). These dynamic interactions within the model result in a new steady-state Ca²⁺ balance (via a feedback from the ΔAP rate to Δfrequency of I_CaL activation). In short, these interactions wax in case of β-AR stimulation but wane upon ChR stimulation.

While the diastolic spontaneous release is a novel and critically important factor in autonomic rate regulation, as shown experimentally (32, 49, 50) and in our model simulations (Figs. 3 and 6), specific biophysical mechanisms that regulate spontaneous SR Ca²⁺ release, per se, have not yet been established for SANCs (or for any other cell type, for that matter). However, our model does explore, in detail, how spontaneous diastolic Ca²⁺ release emerges and how it is specifically modulated in simulations of β-AR and ChR stimulations (see Detailed Numerical Analysis of How β-AR and ChR Stimulation Modulate Spontaneous SR Ca²⁺ Release in the Submembrane Compartment and Fig. 7). Our model predicts that the characteristics of diastolic release are regulated by a complex dynamic interplay of SR Ca²⁺ loading and Ca²⁺ changes in the submembrane space. In short, while spontaneous, localized (within the submembrane space), diastolic Ca²⁺ release is initiated by a rising Ca_jSR (i.e., by SR Ca²⁺ refilling), a subsequent strong increase and synchronization of local Ca²⁺ releases is due to rising Ca_sub (i.e., a secondary release, or Ca²⁺-induced Ca²⁺ release). The earlier and stronger diastolic Ca²⁺ release in the case of β-AR stimulation but later and smaller release in the case of ChR stimulation in our simulations (Figs. 3 and 6) and previous experimental studies, in fact, can be explained by different degree of diastolic Ca²⁺-release synchronization (i.e., synchronization of openings of RyRs).

In the case of β-AR stimulation (Fig. 7), spontaneous Ca²⁺ release can be a threshold event when it involves an “explosive” Ca²⁺-induced Ca²⁺-release mechanism in a small volume, like the submembrane space (the SR is separated from sarcolemma by 20 nm in our model). However, the predicted release synchronization of Ca²⁺ release by RyRs can still be graded by the rate of SR Ca²⁺ refilling, because this ultimately determines the SR Ca²⁺ load at which the spontaneous release is initiated as well as the dynamics of the subsequent diastolic release (j_SRCarel panel in Fig. 7). Our model predicted that β-AR stimulation leads to a larger loading of the junctional SR (Ca_jSR panel in Fig. 7) and network SR (not shown). An increase in SR Ca²⁺ loading in the presence of isoproterenol has also been experimentally demonstrated by an increase in caffeine-induced Ca²⁺ transients in spontaneously beating rabbit SANCs (49).

It is important to note that both increases in intrinsic pump characteristics (P_up) and Ca²⁺ to be pumped (provided via I_CaL) are required to effect the SR Ca²⁺ load increase in our model (Fig. 8). In fact, a substantial component of Ca²⁺ influx via L-type Ca²⁺ channels is likely pumped directly into the SR (22). Thus, additional net Ca²⁺ to increase the SR Ca²⁺ load must eventually occur via sarcolemmal Ca²⁺ influx. During steady-state AP firing during β-AR stimulation, the larger net Ca²⁺ influx is due to not only I_CaL increase per se (i.e., each cycle) but a more frequent I_CaL activation at a higher AP rate (over a period of time, say, 1 min; Fig. 8). This greater net Ca²⁺ influx via I_CaL balances the grater Ca²⁺ efflux from the cell via the larger NCX. When ChRs are stimulated, similar mechanisms, but operating in the opposite direction, produce the SR Ca²⁺ loading decrease (Fig. 8). Our model predicted that in the presence of 100 nM ACh, SR Ca²⁺ loading substantially drops (Ca_jSR panel in Fig. 7). This modulation of SR Ca²⁺ loading is an important model requirement to support larger (or smaller) amplitude diastolic releases, diastolic inward I_NCX, and DD acceleration (or deceleration) commensurate beating rate changes (Fig. 8).

An important question is whether the documented capacity of phospholamban regulation matches the predicted range of P_up to support physiological rate regulation. According to Eq. 6 (solid curve in Fig. 4A), SR Ca²⁺ pump inhibition at 100 nM ACh results in a P_up decrease from its basal state value of 12 to 7.58 mM/s. On the other hand, simulation of the effect of β-AR stimulation requires P_up doubling from 12 to 24 mM/s. Thus, GPCR stimulation in our model requires a 3.2-fold range for P_up changes (from 7.58 to 24 mM/s). Experimental studies, however, have shown that P_up modulation via phospholamban phosphorylation is limited only to two to three times [depending on Ca_i (5)]. Although this is close to our predicted limit, this still indicates that phospholamban/PKA signaling is likely further amplified and/or complemented by some additional factors, such as CaMKII signaling and phosphorylation-dependent effects on RyR activation characteristics, which are not included in our model (dashed lines in Fig. 8; see also Model Limitations and Future Developments below). For example, if β-AR stimulation increases the likelihood for intrinsic activation of RyRs (resulting in a Ca²⁺ spark increase via local RyR recruitment) in SANCs similar to that in ventricular myocytes (59), this would result in a more synchronized Ca²⁺ release at a given SR Ca²⁺ load.

Possible Role of I_f and “Window” or Subthreshold I_CaL in Rhythm Stabilization at Low Rates During ChR Stimulation

While the I_f amplitude decreases upon ChR stimulation (Fig. 6A), the I_f contribution becomes more persistent at longer cycle lengths, thus acting as a “stabilizer” of the pacemaker rate [a concept that was first proposed by Noble et al. (41)]. Our interpretation of the role of I_f as a rate stabilizer (by preventing excessive membrane hyperpolarization; see Fig. 8), especially at low rates and rate transitions, rather than the major rate regulation mechanisms (as previously thought, see the Introduction; via “Δ Early DD” in Fig. 8, dotted arrow) is in line with the recent findings in HCN4 (I_f channel) knockout mice (16) and mice with the absence of cAMP sensitivity of I_f (1). Furthermore, a gradual subthreshold diastolic I_CaL increase (Fig. 6A and Supplemental Fig. S2), albeit with a slightly smaller amplitude than in the basal state, may also act as another stabilizer of the pacemaker cell system function. During ChR stimulation, I_CaL becomes as much as I_NCX at the end of DD, e.g., 8.1 vs. 8.7 pA at −40 mV (Fig. 6A). Another interesting model finding was that when the diastolic Ca²⁺ release becomes insufficient to synchronize itself via Ca²⁺-induced Ca²⁺ release in the submembrane space, the Ca²⁺ flux of this persistent subthreshold I_CaL becomes a major contributor to the late diastolic Ca_sub elevation and, hence, also indirectly activates late diastolic I_NCX to support late DD (compare I_CaL and j_SRCarel panels, both in pA, in Fig. 6A).

Role of I_KACh Activation During ChR Stimulation

The comparison of the two dose-response curves (“All mechanisms” and “All mechanisms except I_KACh” curves) in Fig. 5 revealed that the effect of I_KACh blockade is relatively small at low [ACh]. For example, at 20 nM ACh, the respective rate reductions are 6% versus 7.4%, i.e., an ∼19% difference, consistent with the experimental results that the I_KACh contribution becomes evident only at [ACh] > 30 nM (32). At [ACh] = 100 nM, I_KACh provides a major contribution to the rate decrease (about one-half of the full effect, 17.5% vs. 40%; Fig. 5), also consistent with the most recent experimental results of ACh-induced beating rate reduction in the presence of I_KACh blockade with tertiapin-Q (32). Previous experimental and theoretical studies (4, 6, 9, 20, 32) have shown that the I_KACh mechanism dominates in the negative chronotropic effect at higher ACh concentrations (∼1 μM, not studied here).

Comparisons With Other SANC Models

Curiously, despite extensive theoretical studies of cardiac pacemaker function [since 1960 (39)] in numerous numerical SANC models (54), only two model studies (6, 18), to our knowledge, have numerically explored the effect of β-AR stimulation. The 1999 Demir et al. model (6) of the rabbit SANC, however, was based on a previous 1994 Demir et al. model (7) of the SANC. Following an even earlier (1987) modeling study of atrial myocytes by Hilgemann and Noble (17), the Ca²⁺-release activation in the 1994 model was triggered by membrane depolarization, thereby assuming, by definition, the dominance of membrane mechanisms in cardiac pacemaker function. This type of Ca²⁺ release, however, was later found to be a key feature of skeletal muscle rather than cardiac muscle (13). Based on the knowledge of SANC ion currents at that time, it was also suggested that the spontaneous SANC firing rate is controlled mainly via cAMP-dependent, hyperpolarization-activated current (I_f), which regulates the slope of early DD (6). Late DD in many classical SANC models, including the 1994 Demir et al. model, is greatly contributed by T-type Ca²⁺ current (I_CaT) and voltage-gated Na⁺ current (I_Na). Both I_Na and I_CaT have low voltage activation thresholds and, therefore, strongly amplified the initial cAMP-sensitive signaling of I_f-induced early depolarization in the 1999 Demir et al. model (6). However, I_CaT was later found to be relatively small and detected only in 20% of rabbit SANCs (38); I_Na is negligible in primary/central rabbit SANCs (initiating excitations in the sinoatrial node). Furthermore, being cAMP/PKA independent, I_CaT cannot control late DD and the pacemaker rate.

Another, more recently proposed mechanism of the β-AR stimulation effect via a nonselective current (I_st) has been investigated in the Kyoto model of guinea pig SANCs (18, 44). However, neither the molecular origin nor specific blockers for I_st have not yet been identified; I_st exhibits many properties of I_CaL and I_NCX and, therefore, might not even be a discrete entity [see more in our recent review (27)]. Therefore, if one excludes I_Na, I_CaT, and I_st as major factors in the autonomic modulation of the AP firing rate of primary SANCs, then changes in I_f, I_CaL, and I_Kr seem to be insufficient to numerically explain the effect of β-AR stimulation either in our novel model or in previous classical models (open bars in Fig. 2B). Predictions of these classical SANC models, in fact, greatly vary (Fig. 2B). While increases in I_f and subthreshold I_CaL accelerate the beating rate, the I_CaL increase during AP actually prolongs the AP duration and, hence, decelerates the beating rate (Fig. 8). The effect of an I_Kr increase is also dual (Fig. 8): it facilitates the classic “g_K decay” pacemaker mechanism (39) (accelerating the beating rate) but simultaneously hyperpolarizes maximum diastolic potential (decelerating the beating rate). Thus, the great variability of predictions in previous sinatrial node models can be explained by their different contributions of these “conflicting” ion channel-related mechanisms. Our simulations showed that the experimentally documented AP rate change is linked to diastolic Ca²⁺ release (Figs. 3A, 7, and 8). Except for our recent model (36), this new specific mechanism is absent in at least 12 rabbit SANC models developed so far (for a review, see Ref. 54). Thus, the new LCR-induced I_NCX mechanism coupled to DD acceleration and AP firing rate may be indeed envisioned as the “missing link in the mystery of heart rate regulation” (28) and perhaps explains the paradox of paucity of numerical studies of heart rate regulation by β-ARs.

Cellular mechanisms of AP firing rate downregulation by ChRs have been numerically approached, to our knowledge, in three studies: by Dokos et al. in 1996 (12), by Demir et al. in 1999 (6) (discussed above), and by Zhang et al. in 2002 (58). The latter model simulated the effect of ChR stimulation specifically in central/primary SANCs. The authors assumed that Ca²⁺ dynamics are not important in these cells and set intracellular Ca²⁺ to a constant. A recent study (31), however, has shown that Ca²⁺ cycling is also critical to AP firing of smaller-sized SANCs, which are thought to represent central SANCs (i.e., primary pacemaker cells). Thus, our model simulations here provide the first numerical evidence that Ca²⁺ cycling is indeed a crucial system component that is required to both the rate increase and decrease via stimulation of β-ARs and ChRs, respectively (Fig. 8).

Model Limitations and Future Developments

Limitation 1.

CaMKII signaling has an important role in SANC function (52, 55), and its well-known properties to amplify and integrate Ca²⁺ signaling indicate that it may serve as yet another synergistic coupling factor within the SANC pacemaker system (dashed lines to and from “CaMKII” in Fig. 8). However, there is a paucity of experimental data in SANCs that could be used in the numerical modeling of this signaling pathway. Future modeling of SANC studies ought to explore interactions among multiple regulatory or coupling factors, such as Ca²⁺, CaMKII, and PKA.

Limitation 2.

Basal phosphorylation of RyRs in rabbit SANCs, as assessed by an anti-phosphorylated RyR2 antibody, is substantially higher in rabbit SANCs than in rabbit ventricular cells (50). Also, β-AR stimulation of ventricular myocytes increases the Ca²⁺ spark amplitude (and Ca²⁺ current of a single Ca²⁺ spark) via enhanced recruitment of RyRs (59). These results indicate that the intrinsic characteristics of RyR activation can be modulated in SANCs (dashed lines to and from “RyR” in Fig. 8). However, because of lack biophysical experimental data in SANCs, phosphorylation-dependent changes of RyR were not explored in the present study.

Limitation 3.

Our present model considers only a lumped Ca²⁺ release signal generated by the junctional SR, whereas, in reality, spontaneous Ca²⁺ release is produced by multiple stochastic LCRs by local SR fragments (Figs. 3B and 6B). However, the fine ultrastructure of the SR and the detailed distribution of Ca²⁺ RyRs within SANCs underlying its spontaneous diastolic Ca²⁺ wavelets are presently unknown and require further experimental studies (for pilot attempts to model stochastic LCRs in rabbit SANC, see Ref. 33). Nonetheless, our present approach is sufficient to reproduce the experimentally documented effects of β-AR and ChR stimulation (Figs. 2, 3, 5, and 6) and does not deny or contradict the idea of stochastic LCRs emerging synchronously during DD. Indeed, while each ion channel has stochastic gating, the synchronized action of the channels' ensemble (e.g., an AP) is closely described by simple H-H-type differential equations. The ensemble of SR Ca²⁺-release channels (RyRs) also generates a remarkable macroscopic net signal, the late diastolic Ca²⁺ elevation, observed in the sinoatrial node, a new mechanism of heart rate acceleration via GPCR (23). The novel SANC model described herein reproduces this important macroscopic signal (i.e., an integral of all LCRs within each cycle) and its importance for GPCR modulation (see Figs. 3A and 6A, j_SRCarel panel).

Limitation 4.

Our present model does not describe the kinetics of the evolution of the responses to β-AR and ChR stimulation. Additional experimental data that define the transient state kinetics of cAMP, PKA, and CaMKII signaling in spontaneously firing SANCs are required for systems modeling of biochemistry kinetics to simulate the transitions.

Limitation 5.

Data in the literature have indicated that in addition to Ca_v1.2, Ca_v1.3 is also present in SANCs and is involved in DD (37). Our model, however, is limited to only one I_CaL formulation that integrates both channels. Accurate I_CaL description in future SANC models will need to incorporate the respective, specific formulations for the two I_CaL types (Ca_v1.2 and Ca_v1.3).

GRANTS

This work was supported by the Intramural Research Program of the National Institute on Aging (National Institutes of Health).

DISCLOSURES

No conflicts of interest are declared by the author(s).