On the functional significance of soft modes predicted by coarse-grained models for membrane proteins

Recent years have seen an explosion in the number of studies that explore the collective dynamics of biomolecular systems using coarse-grained (CG) models along with methods based on principal component analysis (PCA). Among them, elastic network models (ENMs) and normal mode analyses (NMAs) have found wide use in several applications. Recent studies are now providing evidence for the usefulness of these methods in exploring the dynamics of membrane proteins. The type of motions explored by the ENMs represents a different regime compared with the highly specific chemical events and electrostatic interactions that are usually explored by molecular dynamics (MD) simulations. These are collective motions that cooperatively involve all subunits, usually exploit the symmetry of the quaternary structure, and facilitate mechanical functions such as pore opening and allosteric communication. Understanding the mechanisms of function of membrane proteins using computational methods may necessitate adopting multi-scale approaches that integrate ENM-based methods with full atomic simulations.

Modeling and simulating the dynamics of membrane proteins is usually a challenge due to the complexity of their interactions with ions, ligands, lipids, and water molecules, and the interplay of chemical and mechanical events at multiple scales that may be controlling their function. The potential of CG models and methods, such as ENM-based NMA, to convey physically and biologically meaningful results concerning membrane protein dynamics and function may therefore be open to discussion, even though such studies prove useful in other applications, e.g., in understanding the role of the intrinsic dynamics of proteins in substrate recognition and binding (Tobi and Bahar, 2005; Bahar et al., 2007; Bakan and Bahar, 2009), the cooperative machinery of supramolecular systems, or the allosteric signaling events at the molecular level (Bahar et al., 2007; Chennubhotla et al., 2008). Here, we present a brief overview of the foundations and basic assumptions of these CG approaches, the motivation and justification behind their use, apart from their simplicity, and what we have learned from the ENM analyses of membrane proteins in recent years (Bahar et al., 2010a).

These studies suggest that, despite the complexity and specificity of their interactions, membrane proteins possess, like other proteins, intrinsic dynamic features that are purely defined by their three-dimensional fold/shape; and like other proteins, they exploit their particular structure-encoded dynamics for achieving key mechanical functions such as gating, pore opening, or allosteric signaling; and ENM-NMA is a uniquely versatile approach for assessing such collective mechanical events and appears as a promising tool to be used in conjunction with other (higher resolution) approaches for elucidating membrane protein dynamics. We also point to the limitations of these approaches and future directions for potential improvement of existing methodologies.

Soft modes define structural rearrangements that are easily accessible, robust, and functional

NMA is not new. Its application to biological systems dates back to the early 1980s. However, only in recent years have the softest modes predicted by NMA been recognized to have biological functional significance. This resulted in a renewed interest in the NMA of biomolecular systems.

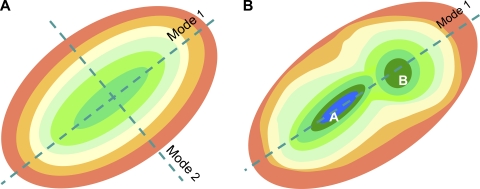
Each normal mode represents a path away from the original global energy minimum in the space of collective coordinates (Fig. 1). Moving along these paths means undergoing collective changes in conformation. Of these accessible paths, one, the lowest frequency mode, also called the global mode or mode 1, requires the least energy for a given deformation, succeeded by mode 2, 3, etc. The mode frequency (squared) represents the curvature (or stiffness) of the multidimensional energy landscape along the mode coordinate. The close neighborhood of the energy minimum is implicitly approximated by a quadratic function along each direction. Low frequency modes are therefore soft modes, easily accessible to the structure.

Figure 1.

Schematic description of the free energy landscape near the equilibrium state at two levels of resolution. (A) CG description, where a single (global) energy minimum is observed. The surface is color-coded from green (lowest energy) to red (highest). In the normal mode description, the energy profile is a quadratic function along each mode axis. Mode 1 axis refers to the direction of motion (away from the minimum) that requires the least ascent in energy for a given displacement. (B) A higher resolution. Two substates, A and B, are distinguished, with lower energy than that observed in the CG model. Substate A is more stable (has lower free energy) than B. Mode 1 directions coincide in both representations.

What NMA does is to uniquely identify these particular directions, or the subset of these most probable collective changes in structure, under the influence of constraints due to chain connectivity and energetics experienced by the molecule.

A schematic representation of the energy landscape in a reduced (two-dimensional) space is shown in Fig. 1. Fig. 1 A displays the CG representation of the energy landscape, where the global minimum is approximated by a smooth function (e.g., harmonic potential) along each mode direction, and Fig. 1 B displays a higher resolution view of the same energy landscape where two minima, or substates A and B, appear. Substates can be, for example, the open and closed forms of a given protein. The substates conceivably contain an ensemble of microstates each (e.g., different loop conformations, different rotameric states of side chains), which are distinguished at even higher resolution. One can therefore think of many hierarchical levels of resolutions, with relatively smooth and shallow representation of the energy landscape at lower resolutions. CG NMA considers the low resolution description with a single global energy minimum as in Fig. 1 A and explores the softest modes near this minimum.

Two important messages are conveyed by Fig. 1. First, the direction of the softest modes (mode 1 in the present case) identified by CG models usually coincides with that obtained with more detailed models. An important aspect of NMA is indeed the robustness of the modes at the low frequency end of the spectrum (Nicolay and Sanejouand, 2006). Robustness means that these modes are not sensitive to structural and energetic details. They are essentially defined by the overall “fold” (i.e., the backbone architecture and/or spatial distribution of residues). They are almost identically reproduced by either full atomic NMA with a detailed force field or a CG description because these are collectively defined by all-atom/residue positions. Perhaps the earliest observation of the robustness of low frequency modes, and definitely the first for a membrane protein, was made by Roux and Karplus (1988), who reported that the low frequency modes of gramicidin A (GA) were insensitive to changes in the strength of hydrogen bond interactions. The computations of Miloshevsky and Jordan (2006) for GA further demonstrated the equivalence of the NMA results from ENMs and those from full atomic models in the presence of explicit lipid and water molecules subject to CHARMM22 force field. And this is despite the fact that GA is a very small protein (two helices of 16 amino acids each), and that ENMs are by definition more applicable to large biomolecules (Gaussian fluctuations become “exact” in the limit of infinitely large networks according to the central limit theorem).

The second message is the fact that coarse-graining of the structure and energetics, and sampling conformations along the softest modes, permit us to possibly sample substates separated by low energy barriers, as illustrated in Fig. 1 B. In a detailed full atomic description, the transition between these states would necessitate the passage over an energy barrier; in the CG description, on the other hand, these substates (which essentially maintain the same fold but exhibit different rearrangements of domains) may become accessible via global fluctuations predicted by NMA. Not surprisingly, the passages between different states of large allosteric systems (e.g., bacterial chaperonin GroEL-GroES; Yang et al., 2009) have been observed in numerous applications to coincide with the soft modes intrinsically accessible to the structure (Bahar et al., 2007, 2010b).

Topology of native contacts is the most important determinant of soft modes, accounted for by network models

Recent studies have shown that of the constraints that define the equilibrium dynamics, one plays a crucial role and almost uniquely defines the softest modes: the three-dimensional geometry, or spatial distribution of residues in the native state, which in turn defines the topology of native contacts. Knowing the topology of contacts means knowing the sequence position of the pairs of residues that make non-bonded (secondary, tertiary, or quaternary) contacts, in addition to those naturally imposed by chain connectivity (bonded pairs). Contacting residues are those within a first interaction shell distance from each other (e.g., 7 Å between α carbons).

Knowledge of this “contact map” directly allows us to construct the so-called Kirchhoff’s matrix of inter-residue contacts, Γ. In the simplest ENM, the Gaussian network model (GNM) (Bahar et al., 1997), Γ is an N × N matrix for a protein of N residues. Its elements Γ_ij are equal to −1 if residues i and j make contacts and 0 otherwise. The positions of the network nodes are identified with those of the α carbons. Springs (of uniform force constant γ) connect contacting residues. Thus, Γ can be readily constructed for any Protein Data Bank (PDB) structure, nuclear magnetic resonance (NMR) model, or MD snapshot. It does not necessitate knowledge of more than one structure, or detailed knowledge of atomic coordinates, but simply the sequence position of residue pairs that “interact.” Yet, it permits us to determine the intrinsic dynamics of the protein uniquely defined by its native contact topology. Similarly, the basic ingredient in the anisotropic network model (ANM) (Atilgan et al., 2001; Eyal et al., 2006) is the native topology.

What type of information can be learned using the GNM?

The GNM results exclusively depend on Γ. First, the (pseudo) inverse of Γ directly scales with the cross-correlations between residue fluctuations, i.e.,

$$<\Delta {\mathbf{R}}_i.\Delta {\mathbf{R}}_j>=({\text{3k}}_{\text{B}}\text{T}/\gamma ){\left[{\Gamma }^{-1}\right]}_{\mathit{ij}},$$ (1)

and obviously the diagonal elements of the inverse, [Γ⁻¹]_ii, scale with the mean-square fluctuations (MSFs) <(ΔR_i)²> of residues under equilibrium conditions. Eq. 1 results from a rigorous statistical mechanical average over all conformations accessible to the structure, in accord with the original theory set forth by Flory for polymer networks. Alternatively, one can predict the MSFs in inter-residue distances ΔR_ij = ΔR_j −ΔR_i, as

$$<{\left(\Delta {\mathbf{R}}_{\mathit{ij}}\right)}^{\text{2}}>=({\text{3k}}_{\text{B}}\text{T}/\gamma )\{{\left[{\Gamma }^{-1}\right]}_{\mathit{ii}}+{\left[{\Gamma }^{-1}\right]}_{\mathit{jj}}-2{\left[{\Gamma }^{-1}\right]}_{\mathit{ij}}\},$$ (2)

using Eq. 1. This quantity is important, as it refers to distance changes “measurable” in single-molecule (e.g., FRET, ESR) experiments. The cross-correlations, <ΔR_i · ΔR_j>, and MSFs in residue positions, <(ΔR_i)²>, form the respective off-diagonal and diagonal elements of the N × N covariance matrix, C^(N). The normalized covariance, ${\text{C}}^{\mathit{(N)}}{|}_{\mathit{norm}}=<\Delta {\mathbf{R}}_i.\Delta {\mathbf{R}}_j>/{[<\Delta {\mathbf{R}}_i.\Delta {\mathbf{R}}_i><\Delta {\mathbf{R}}_j.\Delta {\mathbf{R}}_j>]}^{1/2}$, provides information on purely orientational couplings.

Second, the eigenvalue decomposition of Γ readily gives us information on the contributions of individual modes, in particular including those of the soft modes, to the collective dynamics of the examined system. In terms of the nonzero eigenvalues λ_k and eigenvectors u^(k) (k = 1, N − 1) of Γ, the cross-correlation driven by mode k is

$$<\Delta {\mathbf{R}}_i.\Delta {\mathbf{R}}_j>{|}_k=(3{\text{k}}_{\text{B}}\text{T}/\gamma ){\lambda }_k^{-1}{\left[{\mathbf{u}}^{\left(k\right)}{\mathbf{u}}^{\left(k\right)\text{T}}\right]}_{\mathit{ij}}.$$ (3)

Hinge sites predicted by the GNM and their role in inhibitor/ligand binding and allosteric signaling

The shape/profile of a few softest modes in general, or top-ranking nondegenerate modes in multimeric structures, disclose domain separations and hinge sites. The shape of mode k is quantified by plotting the elements [u^(k)]_i of u^(k) against residue index i. The crossovers between positive and negative points in this curve demarcate the domain separations or the hinge sites for that particular mode. GNM analysis thus entails the examination of a small subset of low frequency modes to identify domains, their cross-correlations, and the hinge sites that mediate their movements. Note that the GNM eigenspace is N-dimensional, as opposed to the 3N-dimensional space explored by ANM (see below).

Proteins usually tolerate mutations/perturbations at many positions, but those at the hinge sites are most likely to impair the collective motions. Not surprisingly, these sites serve as targets for inhibitor or ligand binding. In many cases, it is important to couple the biochemical and mechanical activities, hence the spatial proximity of the global hinge sites and the catalytic residues in enzymes (Yang and Bahar, 2005). In other cases, their central positioning at domain–domain interfaces plays a key role in allosteric communication (Chennubhotla and Bahar, 2007). A typical example is the salt bridge E461-R452, occupying a hinge position between the cis and trans rings of the bacterial chaperonin GroEL, which blocks the release of the co-chaperonin >50 Å away if broken (Chennubhotla et al., 2008). The GNM is currently used for a broad range of purposes: the automated calculation of MSFs, cross-correlations or mode shapes for any PDB structure (Yang et al., 2006), assisting in docking simulations (Ertekin et al., 2006; Andrusier et al., 2008; Gerek and Ozkan, 2010), and characterizing the common dynamics of families of proteins (Leo-Macias et al., 2005; Shrivastava and Bahar, 2006; Rader and Harrell, 2008), to name a few.

The ANM analysis: an efficient approach for exploring global changes in structure

The ANM (Atilgan et al., 2001; Eyal et al., 2006) is a CG NMA. The 3N × 3N counterpart of GNM Γ is the ANM Hessian matrix H, the elements of which are conveniently expressed as N × N submatrices, each of size 3 × 3. The xy^th element of the ij^th submatrix (i ≠ j) is the second derivative

$$\frac{{\partial }^2{V}_{\mathit{ANM}}}{\partial x_i\partial y_j}=-\frac{\gamma \left(x_j^0-x_i^0\right)\left(y_j^0-y_i^0\right)}{{\left(R_{\mathit{ij}}^0\right)}^2}$$ (4)

of the potential V_ANM = 1/2 Σ_i Σ_j γ(R_ij − R_ij⁰)², where R_ij and R_ij⁰ are the instantaneous and equilibrium distances between the α carbons i and j; x_i^o, y_i^o, and z_i^o are the components of the distance vector R_ij⁰; and the summation is performed over all residues 1 ≤ i < j ≤ N that make contacts (or connected by a spring in the network). The diagonal submatrices of H are equal to the negative sum of off-diagonal submatrices. The 3N–6 nonzero eigenvalues, σ_k, and eigenvectors, v^(k), of H define the set of ANM modes accessible to the structure. The 3N elements of v^(k) describe the three-dimensional directional vectors of the N residues of the protein as the molecule reconfigures in the k^th mode. The size of the motion in mode k scales with σ_k^−1/2. ANM takes advantage of these “unit displacements” to generate alternative conformations:

$$\left\{\mathit{R}(s,k)\right\}=\left\{{\mathit{R}}^0\right\}\pm s{\sigma }_k^{-1/2}{\mathit{v}}^{\left(k\right)},$$ (5)

where {R⁰} denotes the 3N-dimensional vector of the original position vectors of all residues, also called original configuration vector, and {R(s, k)} is the new configuration vector, reached upon moving along mode k by a magnitude sσ_k^−1/2 . Here, s is a parameter that scales the amplitude of the motion. Note that the NMA with CG models cannot predict the absolute size of the motion in the absence of quantitative knowledge on γ, but its “direction” only. Likewise, the sense of the motion, positive or negative, along a given direction, is equally probable because these are fluctuations, by definition, hence the use of ±s in Eq. 5. The above expression is used to generate movies of collective motions, as may be viewed in the ANM server (Eyal et al., 2006).

Finally, the inverse of H defines the 3N × 3N covariance matrix, C^(3N), the elements of which are

$${\left[{\mathit{C}}^{\mathit{(3N)}}\right]}_{\text{ij}}=\left({\text{k}}_{\text{B}}\text{T}\right){\mathbf{H}}^{-1}=\left({\text{k}}_{\text{B}}\text{T}\right){\Sigma }_k{\sigma }_k^{-1}{\left[{\mathit{v}}^{\left(k\right)}{\mathit{v}}^{\left(k\right)T}\right]}_{\text{ij}}.$$ (6)

The covariance matrix C^(3N), or its top-ranking eigenvectors v⁽¹⁾, v⁽²⁾, v⁽³⁾, etc., based on the ANM may be directly compared with the covariance and associated principal components p⁽¹⁾, p⁽²⁾, p⁽³⁾, etc., derived from ensembles of experimentally resolved structures for a given protein (Bakan and Bahar, 2009). This type of comparison is now possible with the accumulation of alternative (functional) structures for well-studied proteins, and provides a useful framework for validating and/or consolidating the ANM predictions and establishing the role of soft modes in protein function.

How many modes? Which modes?

The reciprocal eigenvector, λ_k⁻¹ (in GNM) or σ_k⁻¹ (in ANM), serves as a statistical weight when summing up the contribution of different modes to obtain <ΔR_i · ΔR_j> or MSFs (see Eqs. 3 and 6). Or, alternatively, one may consider each mechanism of motion (collective movement of the molecule along a given mode k, represented by the k^th eigenvector), to be weighted by λ_k^−1/2 or σ_k^−1/2 (Eq. 5). Clearly, slower modes (smaller λ_k or σ_k) make the largest contribution to predicted dynamics. Of interest is to assess to what extent such slow modes account for the experimentally observed (functional) structural changes, or alternatively which modes to choose for modeling the structural changes induced upon substrate/ligand binding (Petrone and Pande, 2006; Sperandio et al., 2010).

Numerous applications in the last decade, starting from the original work of Tama and Sanejouand (2001), have compared the structural change between two structurally resolved forms (e.g., open and closed states) of a given protein, with the soft modes of reconfiguration predicted by ENM-NMA for one of the conformers. A first step in this analysis is the optimal superimposition (using the Kabsch algorithm, for example) of the two known structures to evaluate the 3N-dimensional difference/deformation vector d^(3N)_exp in the absence of rigid-body translation and rotation. Next, d^(3N)_exp is compared with predicted modes, e.g., the ANM eigenvectors v^(k), k = 1, 3N−6. In principle, because the eigenvectors form a complete orthonormal basis set, the correlation cosines squared sum up to unity, i.e., Σ_k (d^(3N)_exp · v^(k)/|d^(3N)_exp|)² = 1 for 1 ≤ k ≤ 3N−6. Of interest is to evaluate this summation over a subset of m modes in the low frequency regime, and in particular for the case m = 1 or 2, to assess the extent of correlation between theory and experiments. Such analyses indicate that a very small subset of soft modes (if not the top 1–3) yields a cumulative overlap of 0.80 ± 0.15 with experimentally observed structural changes (Cui and Bahar, 2006; Bahar et al., 2010a,b).

Although global changes in structure such as coupled domain movements are well accounted for by a few softest ANM modes, local changes in structure may fall below the resolution of ANM (e.g., side chain rotations) or be associated with higher frequency modes. Which mode to consider among the multitude of 3N modes may then become problematic, unless attention is given to a specific site (e.g., inhibitor-binding site), in which case the modes that induce a motion at that particular site can be advantageously selected for sampling alternative conformations. In many cases, soft modes may also entail local effects that affect the “site” of interest. Thus, one can use an ensemble of selected high frequency modes and/or a few in the lowest frequency regime to sample probable conformers at the ligand-binding site. This type of NMA-assisted sampling emerges as a productive approach in modeling protein ligand/drug interactions (Cavasotto et al., 2005; Floquet et al., 2006, 2010; May and Zacharias, 2008; Sperandio et al., 2010).

Proteins resolved in multiple states exhibit structural variations conforming to ANM soft modes

Early studies of protein dynamics have generally used the comparison with crystallographic B factors for benchmarking ENMs. B factors scale with the MSFs of atoms as B_i = (8π²/3)<ΔR_i · ΔR_i>, assuming that the deviations in atomic positions are isotropic. More recent higher resolution structures provide information on anisotropic B factors. Other types of experimental data exploited in previous work include H/D exchange protection factors, folding nuclei, NMR order parameters, and root-mean-square deviations between NMR models, all of which provide information on equilibrium fluctuations or stability.

With the accumulation of structural data in the PDB, on the other hand, there is a much more meaningful way of comparing ENM predictions with experimental data: for many well-studied proteins, the PDB now offers more than one or two conformers; instead, we have “ensembles” of structures. These ensembles reflect the configurational space sampled by these proteins near native-state conditions (Vendruscolo, 2007). For example, HIV-1 reverse transcriptase has been structurally resolved in ∼150 different forms, unliganded or liganded, complexed with inhibitors or oligonucleotides. The different structures exhibit differences in domain positions (e.g., large movements in the thumb subdomain), which usually reflect the functional dynamics of the enzyme. HIV-1 protease, p38 kinase, cyclin-dependent kinase 2, and ubiquitin are other proteins crystallographically resolved in many different forms. Additionally, ensembles of NMR models have been determined for structurally flexible proteins such as ubiquitin and calmodulin, which in turn have been verified to be relevant to functional forms detected in experiments (Best et al., 2006; Lange et al., 2008). The known ensemble of structures for a given protein may be readily used to evaluate the experimental covariance matrix, C^(3N)_exp. The PCA of C^(3N)_exp yields the principal modes of structural changes, p⁽¹⁾, p⁽²⁾, p⁽³⁾. Comparison of these principal modes with those, v⁽¹⁾, v⁽²⁾, v⁽³⁾, predicted by the ANM (for a single “average” structure) demonstrates that (a) the top-ranking three modes usually account for >50% of experimentally observed conformational variability, and (b) the two sets of soft/principal modes exhibit correlations of the order of 0.85 ± 0.10 (Bakan and Bahar, 2009).

Rhodopsin conformers: comparison of theoretical soft modes and experimental variations in structure

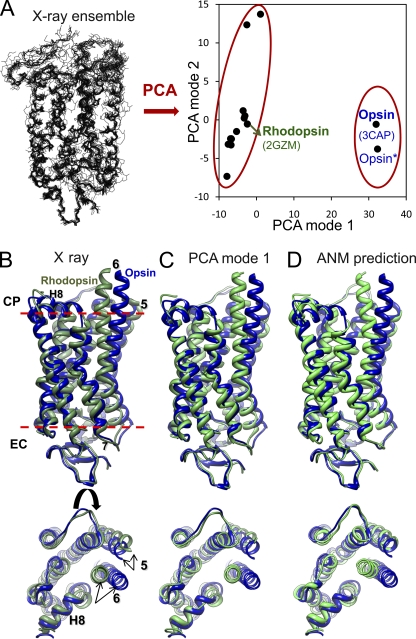
Structural data on membrane proteins are too limited to conduct such systematic analyses for the time being, but there is a rapid growth in the number of known membrane protein structures, with recent advances in structure determination methods and structural genomics initiative. Perhaps one of the most broadly studied membrane proteins is rhodopsin, a prototype and only structurally resolved member of the family of G protein–coupled receptors and an important target for drug development. Rhodopsin activation presumably involves an outward tilt of 6 Å in transmembrane (TM) helix TM6, and pairing of TM5 to TM6, triggered upon cis-trans isomerization of the retinal embedded in a central hinge site (Isin et al., 2006). There has been a remarkable progress in the number of newly solved G protein–coupled receptor structures in recent years. Comparison of the ligand-free (opsin) (Park et al., 2008) and activated (opsin*) structures shows little difference, suggesting that the opsin-conformational population is intrinsically shifted toward the activated state in the absence of retinal and G protein binding. A PCA of currently available 14 rhodopsin and 2 opsin structures (superimposed in Fig. 2 A) shows that p⁽¹⁾ distinguishes the rhodopsin and opsin conformers, whereas p⁽²⁾ yields a dispersion of various rhodopsin structures that differ in the conformations of their loops and chain termini (Bahar et al., 2010a). These two modes account for 62 and 12% of structural variability in the dataset, respectively. Fig. 2 B illustrates the side and top (from the cytoplasmic region) views of rhodopsin (green) and opsin (blue) conformers. In Fig. 2 C, the green conformation is generated by “deforming” the known opsin structure (blue) along p⁽¹⁾. This panel demonstrates that the rhodopsin structure may be reconstructed almost identically by reconfiguring the opsin conformer along this principal mode inferred from experiments.

Figure 2.

PCA and ANM calculations for rhodopsin. (A) PCA analysis of 16 x-ray structures. On the left, backbone conformations are optimally superimposed. On the right, the loci of the examined structures in the subspace spanned by the two top-ranking PCA modes (p⁽¹⁾ and p⁽²⁾) are shown. PCA mode 1 correctly clusters the inactive (rhodopsin) and (putative) activated (opsin) structures into two separate groups. Mode 2 further differentiates the structures in the cluster of inactive rhodopsins. (B) Superimposition of experimentally determined rhodopsin (PDB accession no. 2GZM) and opsin (PDB accession no. 3CAP) conformers viewed from the side (top) and cytoplasmic region (bottom). (C) Rhodopsin structure generated by reconfiguring the opsin along the first PCA mode, viewed from the same two perspectives. (D) Rhodopsin conformation predicted by deforming opsin along the 20 lowest frequency ANM modes. A cutoff distance of 8 Å was adopted in the ANM for defining inter-residue contacts.

The set of rhodopsin/opsin conformers considered here is far from providing a complete representation of the conformational space sampled by rhodopsin. Furthermore, the ANM-predicted soft modes do not contain the global effects/constraints imparted by the lipid bilayer on the membrane protein dynamics. Notwithstanding these deficiencies in both experimental data and theory, ANM calculations performed for a representative opsin structure (PDB accession no. 3CAP, labeled in Fig. 2 B) lead to a cumulative overlap of 0.79 between p⁽¹⁾ and the softest 20 ANM modes. Similar calculations repeated for rhodopsin (PDB accession no. 2gzm) yielded an overlap of 0.74 between p⁽¹⁾ and the softest 20 ANM modes. Thus, although a one-to-one match between PCA modes and ANM modes cannot be seen, it is sufficient to consider 2% of ANM modes (at the low frequency end of the mode spectrum) to closely reproduce the experimentally observed structural changes in either direction. The conformer generated (green) by moving the opsin conformer (blue) along these ANM modes is shown in Fig. 2 D.

Applications to membrane proteins: dominant role of nondegenerate soft modes

The principal changes in structure, or the soft modes, are usually en bloc movements of substructures beyond the fluctuations observed in typical MD runs of tens of nanoseconds. Their time scales vary in the milliseconds to microseconds, usually. Although the capabilities of MD as a method for membrane protein physiology are expected to substantially grow in the future (Dror et al., 2010), there is a need for CG models and methods. And the ability of the ANM to predict most probable large-scale structural changes is particularly important for multimeric membrane protein dynamics. Below, we present a few examples of such applications. For a more extensive review, we refer to Bahar et al. (2010a).

Many membrane proteins are composed of multiple monomers that are symmetrically arranged: potassium channels are tetrameric; aspartate transporter, trimeric; mechanosensitive channels (MscLs), pentameric, etc. Modes that maintain the symmetry of the structure have been noted in previous applications to homo-multimeric systems (e.g., bacterial chaperonin GroEL, or viral capsids) to be most effective in enabling the transition between functional forms. These modes are nondegenerate. They induce the same type of structural change in all subunits. Consistent with these observations, the slowest nondegenerate modes have been observed to relate to functional events in membrane proteins (Bahar et al., 2010a).

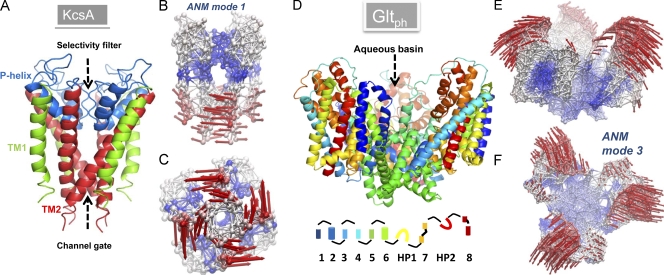
Fig. 3 illustrates two such modes: for the potassium channel KcsA (A–C) and for the archaeal aspartate transporter Glt_Ph (D–F). A global twisting/torsion of all four monomers is seen in the first nondegenerate ANM mode predicted for KcsA (Shrivastava and Bahar, 2006). Such global rotations around the cylindrical symmetry axis normal to the membrane surface appear to be a viable gating mechanism in many other membrane proteins, as shown below. Notably, these motions require minimal displacements in the surrounding lipid molecules involving shear stresses rather than normal stresses.

Figure 3.

Structure and softest modes for the potassium channel KcsA (A–C) and glutamate transporter Glt_Ph (D–F). (A and D) The respective ribbon diagrams of KcsA (PDB accession no. 1K4C) and Glt_Ph (PDB accession no. 1XFH) structures. KcsA is a homotetramer. The outer (TM1) and inner (TM2) helices of each monomer span the bilayer, while the short P helix spans half the bilayer, enclosing the selectivity filter. Glt_Ph is a homotrimer. The diagram at the bottom represents the color code for the eight TM helices, and the two reentrant loops, HP1 and HP2. (B and C) The ANM representation of KcsA, colored-coded by the mobility of residues in ANM mode 1. Blue, almost rigid; red, most mobile. The arrows indicate the direction of motion in this mode. The lower portions of the helices undergo the largest motions, inducing an enlargement in the channel gate lined by the four TM2 helices. (E and F) The ANM results for Glt_Ph in the outward-facing state, colored according to mobility in ANM mode 3 (softest nondegenerate mode). The extracellular regions of the three subunits surrounding the central aqueous basin undergo concerted opening/closing movements to alternatively occlude/expose the central cavity to solvent and solutes.

Glt_Ph exhibits a completely different type of motion (Fig. 3, D–F). The outward-facing structure of Glt_Ph (Boudker et al., 2007) is used in this case to find that the first nondegenerate mode (ANM mode 3) is a concerted opening/closing of the three monomers around the cylindrical axis of symmetry. This mode provides/restricts access to the extracellular region, thus modulating the exposure of the central basin to the exterior (synapse). It also allows for possible inter-monomer contacts between residue pairs that are far (>40 Å) apart in the known crystal structure, particularly those on the helical hairpin HP2 and TM helix TM8 in the core domains, which may affect substrate uptake. Such “distant” residue pairs have been observed to form cross-links in CSLS (cysteine-less) EAAT1 (excitatory amino acid transporter 1, human orthologue of Glt_Ph) mutants upon introducing single-cysteine substitutions (per monomer) at Val449 (Seal et al., 2001). The V449C mutation abolishes glutamate transport. These observations lend support to the existence and significance of the collective opening–closing mechanism predicted by ANM. This mode of motion simultaneously involves all three monomers, in sharp contrast to the localized motions within the core domains of the individual monomers, which are observed in MD simulations to enable extracellular gate opening and substrate binding (Shrivastava et al., 2008; Gu et al., 2009).

It should be noted that the modes of motions shown in Fig. 3 represent one, out of 3N−6, modes accessible to the examined proteins. In both cases, these are the “softest” modes that induce a symmetric change in structure in the neighborhood of the starting energy minimum. They are presumed to be critically important due their cooperative nature and large contribution to observed dynamics. However, they are certainly complemented by other modes to enable the biological function of the molecule. For example, the mechanism in Fig. 3 (D–F) is not conducive to an inward-facing state, which is required to release the substrate (and co-transported Na⁺ ions) to the cytoplasm during the glutamate translocation cycle. The recent elucidation of the inward-facing conformation for Glt_Ph (Crisman et al., 2009; Reyes et al., 2009) reveals that a concerted translation of the core domains perpendicular to the plane of the membrane takes place during the transition from the outward-facing to the inward-facing state, which rigidly “lifts” the substrate-binding site to the vicinity of the cytoplasm. Comparison of this conformational change d^(3N)_exp with the ANM eigenvectors v^(k) evaluated for the outward-facing Glt_Ph yields a cumulative correlation cosine of ∼0.80 using the slowest k = 60 modes out of the complete set of 3N−6 > 3,600 modes (Zomot et al., 2010), in support of the functional significance of the slowest modes.

Global torsion/twisting proposed as a pore-opening mechanism in ion channels

GA.

One of the earliest NMA of membrane proteins using ENMs is that of GA (Miloshevsky and Jordan, 2006). This study showed that channel gating was achieved by the counter-rotation of the two left-handed head-to-head stacked helices. In this case, the channel itself is formed by the inner walls of the left-handed helices. This movement was pointed out to be an inherent property of the GA architecture, independent of surrounding lipid and water molecules. An important observation, also revealed by the earlier NMA of Roux and Karplus (1988), was the insensitivity of the soft modes to model and parameters. In a related study, Langevin dynamics calculations (similar to NMA, but in the phase space of displacements and momenta) were repeated for the fully atomic model and a mixed model with a low resolution ENM to verify that the results from two sets closely agreed in support of the applicability of the CG description (Essiz and Coalson, 2007). All of these studies provide compelling evidence that the directionality of the soft modes natively accessible to GA is predominantly an intrinsic property defined by the protein architecture, not significantly altered by the solvent and/or lipid environment, nor the use of simplified potentials.

Potassium channels KcsA, KvAP, Shaker, MthK, KirBac1.1, and the cation channel NaK.

Likewise, our ANM calculations for the core domains of five potassium channels, KcsA, KvAP, Shaker, MthK, and KirBac1.1, showed (Shrivastava and Bahar, 2006) that all five core domains share a common soft mode, mainly a concerted rotation/twisting of all four M2 helices, which cooperatively induces pore opening (Fig. 3, A–C). The relative rearrangements of the M2 helices induced by this mode are in agreement with the SDSL EPR data from Perozo et al. (1999). Notably, the recently resolved structure of the cation channel NaK in the open form (Alam and Jiang, 2009) revealed a kink formation at G87 as a mechanism that facilitates pore opening, consistent with the hinge role we predicted (Shrivastava and Bahar, 2006) for the counterpart of this conserved glycine in different K⁺ channels (G83 in MthK, G99 in KcsA, and G134 in KirBac1.1). Furthermore, a comparison of the open and closed forms of NaK discloses a global twisting motion (Alam and Jiang, 2009) that maintains the conformation of the selectively filter almost rigidly, in accord with the ANM predictions (Shrivastava and Bahar, 2006).

MscL.

The ANM analysis of the pentameric MscL from Escherichia coli (Valadié et al., 2003) identified two major kinds of motions: Type I, a symmetrical motion that corresponds to an overall twisting during which the extracellular and cytoplasmic regions undergo counter-rotations about the cylindrical axis, driven by the first nondegenerate ANM mode; and Type II, a global bending, via modes 2 and 3. The former “twist to open” motion is consistent with the iris-like mechanism proposed by Sukharev et al. (2001) to be implicated in the gating process. On the other hand, the second nondegenerate mode enables the contraction/expansion of the channel along the axial direction. The associated mode profile exhibits a correlation cosine of ∼0.70 with the structural change observed between the open and closed forms of the MscL, as illustrated in our recent review (Bahar et al., 2010a).

Nicotinic acetylcholine receptor (nAChR).

Another protein studied by ENMs is the nAChR, a ligand-gated ion channel, with acetylcholine itself serving as the ligand that triggers a transient opening of the channel pore at a distance of ∼40 Å, thus allowing cations, particularly Na⁺ and K⁺, to pass through. NMAs performed for the intact nAChR (Szarecka et al., 2007) and for the homopentameric α₇nAChR models (Taly et al., 2005; Cheng et al., 2006) invariably showed that the softest mode is a concerted quaternary twist around the fivefold symmetry axis. In particular, the counterclockwise rotation of the TM domain (accompanied by clockwise rotation of the EC domain) when viewed from the CP region, induces an increase in the diameter (5.7 Å) of the constriction zone between the M2 helices lining the TM channel. This opening is sufficient to permit the passage of monovalent cations, the first hydration shell of which is around 8 Å (Taly et al., 2005). The collective rotation of the M2 bundle was also indicated by the PCA of MD trajectories (Hung et al., 2005). The consistency between NMA soft modes obtained in the absence of lipid environment and the essential modes from MD simulations in explicit water and lipid bilayer support the dominance of the intrinsic dynamics of AChR, in defining the gating mechanism.

On the limitations, applicability, and future extensions of ENM-based studies of membrane proteins

The ENM-NMA results are obtained on the basis of the membrane protein geometry/shape (or topology of native contacts), exclusively, and assume no damping of motions. No interactions with the lipid and water molecules are taken into consideration. Yet, the soft modes from such analyses correlate well with experimentally observed structural changes. These results suggest that membrane proteins are not that different from other biomolecular systems insofar as the robustness and functional significance of their soft modes is concerned. The soft modes predicted by ANM appear to facilitate, if not enable, events such as pore opening or allosteric signaling. The predicted mechanisms are consistent with alternative structures resolved for the protein. For example, the quaternary twist mode of nAChR compares favorably with the structural difference observed between the closed (ELIC) and open (GLIC) ligand-gated ion channel structures (Bocquet et al., 2009; Hilf and Dutzler, 2009); the global twisting of potassium channels is in accord with SDSL-EPR data (Perozo et al., 1999) and the structural change observed between the open and closed forms of NaK (Alam and Jiang, 2009); or the structural change to the inward-facing state is accounted for by <2% of modes accessible to Glt_Ph in the outward-facing state.

These observations seem to challenge the well-established concept that precise modeling and evaluation of detailed atomic (and ionic) interactions in explicit membrane and solvent is essential for simulating membrane protein dynamics. There is no question that such detailed models are needed to explore many events in membrane proteins or biomolecular systems, in general. The answer resides on the identity/type/scale of motions that are being explored. The passage of ions through the selectivity filter in KcsA, or the selective channeling of potassium over sodium ion, for example, cannot be understood unless detailed MD runs with explicit water and lipid molecules in the presence of a detailed force field are performed; or the opening of the EC gate (hairpin HP2) followed by the recognition and binding of the substrate are events that could not be observed if it were not for the detailed, expensive simulations of events at atomic scale. Specific interactions may require the use of polarizable force fields or quantum mechanical calculations. As a rule of thumb, all events involving chemical changes or specific interactions would necessitate the adoption of such detailed models and methods.

However, there is also a completely different class of movements, which may be viewed as “mechanical” processes. In contrast to chemical events that are usually localized, mechanical events may easily embody the entire multimeric structure, or hundreds of residues. Rather than internal/enthalpic interactions, they are mainly driven by entropic effects. Their cooperative nature (and slow dynamics) makes them hard to be seen in conventional MD simulations. ENMs appear to be uniquely suited to unravel such collective mechanics, and the ANM server (Eyal et al., 2006) may be readily used in most applications. Key to their success are the consideration of the spatial distribution of all residues in the multimer and the derivation of a unique solution for each topology, which takes (mathematically rigorous) account of the coupling/connectivity between all bonded and nonbonded pairs.

Are chemical and mechanical events decoupled? If so, one can perform modeling analyses in some approximate ways. However, in many cases, events at multiple scales are coupled, and the challenge is to develop purely integrative methods that take into account both local and global events. Several attempts in this direction are underway, such as methods that use ANM modes for steering MD runs (Isin et al., 2008) or constraining replica exchange MD simulations (Gerek and Ozkan, 2010) or normal-mode Langevin dynamics simulations (Essiz and Coalson, 2007; Sweet et al., 2008). Other methods aimed at improving the capability of ENM-based approaches include the extraction of ENM force constants from MD runs (Moritsugu and Smith, 2007) and the sampling of transition pathways using adaptive ANM (Yang et al., 2009) in conjunction with Monte Carlo simulations (Kantarci-Carsibasi et al., 2008). Essential to further development of ENM-based methodology is a systematic establishment of ENM parameters and algorithms toward accurate incorporation of the effect of membrane environment on the collective modes of the protein. Efforts in this direction are also underway (Ayton et al., 2010). Progress in this field is expected to have significant impact on computer-aided discovery of small molecule inhibitors that target membrane proteins and on the refinement of low resolution (e.g., cryo-EM) structures.