Evaluation of remifentanil sevoflurane response surface models in patients emerging from anesthesia: Model improvement using effect-site sevoflurane concentrations

Abstract

Introduction

We previously reported models that characterized the synergistic interaction between remifentanil and sevoflurane in blunting responses to verbal and painful stimuli. This preliminary study evaluated the ability of these models to predict a return of responsiveness (ROR) during emergence from anesthesia and a response to tibial pressure when patients required analgesics in the recovery room. We hypothesized that model predictions would be consistent with observed responses. We also hypothesized that under non steady state conditions, accounting for the lag time between effect site (Ce) and end tidal (ET) sevoflurane concentrations would improve predictions.

Methods

Twenty patients received a sevoflurane, remifentanil, and fentanyl anesthetic. Two model predictions of responsiveness were recorded at emergence: an ET based and a Ce based prediction. Similarly two predictions of a response to noxious stimuli were recorded when patients first required analgesics in the recovery room. Model predictions were compared to observations with graphical and temporal analyses.

Results

While patients were anesthetized, model predictions indicated a high likelihood that patients would be unresponsive (≥ 99%). However, following termination of the anesthetic, models exhibited a wide range of predictions at emergence (1% to 97%). Although wide, the Ce based predictions of responsiveness were better distributed over a percentage ranking of observations than the ET based predictions. For the ET based model, 45% of the patients awoke within 2 minutes of the 50% model predicted probability of unresponsiveness; 65% awoke within 4 minutes. For the Ce based model, 45% of the patients awoke within 1 minute of the 50% model predicted probability of unresponsiveness; 85% awoke within 3.2 minutes. Predictions of a response to a painful stimulus in the recovery room were similar for the Ce and ET based models.

Discussion

Results confirmed in part our study hypothesis; accounting for the lag time between Ce and ET sevoflurane concentrations improved model predictions of responsiveness but had no effect on predicting a response to a noxious stimulus in the recovery room. These models may be useful in predicting events of clinical interest but large scale evaluations with numerous patients are needed to better characterize model performance.

INTRODUCTION

Population models characterizing the pharmacodynamic interactions between hypnotics and opioids such as propofol and remifentanil can be applied clinically to predict drug behavior in individual patients.(1) We previously reported a series of response surface models that characterized the synergistic interaction between predicted remifentanil effect-site concentrations and measured end-tidal sevoflurane levels in blunting responses to selected verbal and painful stimuli.(2) The aim of this study was to evaluate the ability of these models to predict the return of responsiveness (ROR) in patients undergoing elective surgery during emergence from anesthesia and a response to tibial pressure when patients required analgesics in the recovery room. We hypothesized that model predictions would be consistent with observations. One limitation to these models was that measured end-tidal sevoflurane concentrations do not reflect brain concentrations during non steady-state conditions such as emergence from anesthesia. We also hypothesized that response surface model predictions would improve if we account for the lag time between brain and end-tidal sevoflurane concentrations.

METHODS

Section I: Response Surface Model Development

We revised previously reported sevoflurane-remifentanil pharmacodynamic interaction models.(2) We modified the models to account for the lag time between changes in end-tidal and brain sevoflurane concentrations during non steady-state conditions. A physiologic model was used to predict brain concentrations during non-steady-state conditions. In response to a step change in inspired sevoflurane, predicted brain concentrations were slower to change than end-tidal measurements. We also revised the models to account for the effect of altitude (the original model was based on data collected at 5000 feet above sea level).

Two sets of revised response surface models were constructed: one set using predicted remifentanil effect-site concentrations and measured end-tidal sevoflurane levels and a second set using predicted remifentanil effect-site concentrations and predicted sevoflurane effect-site levels. Each set consisted of two models: a probability of unresponsiveness model (i.e. lack of response to loud verbal and non-painful tactile stimuli based on the observers’ assessment of alertness and sedation scale (OAA/S) presented in Table 1) (3) and a lack of response to 30 PSI of anterior tibial pressure (pressure algometry) model. 30 PSI was used in lieu of 50 PSI as in our prior work(2) because our recent experience suggests that 30 PSI is a better surrogate for the painful stimuli encountered in the recovery room. In our recent work we found that 50 PSI was too strong a stimulus when compared to stimuli typically encountered in the recovery room.(1)

Table 1.

The Observers Assessment of Alertness/Sedation (OAA/S) score.(3)

Value	Description
5	Responds readily to name spoken in normal tone.
4	Lethargic response to name spoken in normal tone.
3	Responds only after name is called loudly and/or repeatedly for the individual to open their eyes.
2	Responds only after moderate prodding or shaking.
1	Does not respond to moderate prodding or shaking

An Observer’s Assessment of Alertness/Sedation score of 1 was considered unresponsive.

A pharmacokinetic model for inhalation agents was used to account for the lag between sevoflurane effect-site concentrations and end-tidal concentrations.(4,5) Model development is presented in Appendix I.

The response surface models were constructed using a Greco model structure (equation 1).(6,7) This structure differs from the Logit model structure we originally used to characterize interactions between remifentanil and sevoflurane.(2) The Greco model structure was used to build a revised set of models to be consistent with our prior work with evaluating propofol-remifentanil response surface models in surgical patients.(1) Models were built using a naïve pooled technique.(8)

$$\mathit{Effect}=\frac{E_{max}•{\left[\frac{C_{e}r}{C_{50r}}+\frac{C_{e}p}{C_{50p}}+\alpha •\left(\frac{C_{e}r}{C_{50r}}•\frac{C_{e}p}{C_{50p}}\right)\right]}^n}{{\left[\frac{C_{e}r}{C_{50r}}+\frac{C_{e}p}{C_{50p}}+\alpha •\left(\frac{C_{e}r}{C_{50r}}•\frac{C_{e}p}{C_{50p}}\right)\right]}^n+1}$$ (1)

E_max is the maximal effect (i.e. no response to pressure algometry), C_50s (sevoflurane) and C_50r (remifentanil) are the concentrations that produce 50% of the maximal effect when administered individually, n is the slope of the pharmacodynamic response curve, and α is the interaction between sevoflurane and remifentanil. Effect ranged from 0 (0% probability of no response) to 1 (100% probability of no response). Model parameters were identified by an iterative process in which the log likelihood between the observations and the model predictions was maximized (Matlab, The MathWorks, Inc., Natick, MA). Coefficients of variation were estimated for each parameter using a bootstrap method with 10000 iterations.(9)

An assessment of how well the revised models fit observations in our volunteer study was made by calculating the percentage of predictions greater than 0.5 (response or no response) that agreed with observations. Responses were compared to model predictions using a Spearman rank correlation (rho). A two-tailed unpaired t-test was used to determine whether the Spearman rho was significantly different from 0. The null hypothesis was that the revised models did not correlate with observations.

Section II: Evaluation of Response Surface Models in Patients Undergoing Elective Surgery

Patient Selection

After Institutional Review Board approval at the University of Utah, informed consent was obtained from 20 patients presenting for elective surgery. Twelve male and 8 female subjects participated. Patients with a history of ongoing opioid consumption were excluded. Age, weight, and height were recorded for each patient.

Patient Monitoring

Each patient was instrumented with a pulse oximeter, noninvasive blood pressure cuff set to cycle every 5 minutes, a five lead electrocardiogram, and an oral or nasal temperature probe. Inspired and expired sevoflurane concentrations were continuously monitored (AS/3 Anesthesia Monitor, Datex-Ohmeda, Helsinki, Finland) and stored every 5 seconds using a computerized data acquisition system (S/5 Collect, Datex-Ohmeda, Helsinki, Finland).

Experimental Protocol

Midazolam 12.5 mcg/kg was administered intravenously in the preoperative holding area 10 minutes before patients were then taken to the operating room. Induction consisted of age adjusted infusions of remifentanil (range 0.1 to 0.5 mcg/kg/min) and propofol (range 75–300 mcg/kg/min) designed to achieve a loss of response to laryngoscopy within 7 minutes (Medfusion 2010I or 3010I, Medex Inc, Duluth, GA).(1)

Following loss of responsiveness, patients received either rocuronium (0.6 mg/kg) or succinylcholine (2 mg/kg) followed by tracheal intubation. The propofol infusion was terminated after tracheal intubation. Maintenance of anesthesia consisted of remifentanil and sevoflurane titrated at the anesthesiologist’s discretion. Prior to emergence, anesthesiologists administered fentanyl as per their standard practice to manage post operative pain.

During emergence, level of responsiveness was assessed using the OAA/S every 20 seconds by calling the patient’s first name and asking “Can you open your eyes?”. If there was no eye opening the question was repeated. If still unresponsive, the question was asked a third time while shaking the patient’s shoulder for 2 seconds. Assessments began when the remifentanil infusion and the sevoflurane vaporizer were both turned off. They ended when the patient regained responsiveness. ROR was defined as the first of two consecutive OAA/S scores > 1.

Patients were observed in the recovery room for 30 minutes. Every five minutes a study nurse asked the patients to use the visual analog scale (VAS) to give a pain score and a pain score that the patients considered tolerable. Fentanyl was administered in 0.5 to 2 mcg/kg increments when the actual VAS was greater than the tolerable VAS and the recovery room nursing staff considered it appropriate (i.e. lack of excessive sedation or respiratory depression).

Pharmacokinetic Simulation

Time-stamped data files of drug administration with a resolution of 5 seconds were used to predict fentanyl(10) and remifentanil(11) effect-site concentrations. Fentanyl effect-site concentrations were converted to equivalent remifentanil effect-site concentrations using a relative potency of remifentanil to fentanyl = 1:1.2.(12,13) Measured end-tidal sevoflurane concentrations were used to predict sevoflurane effect-site concentrations. Pharmacokinetic models for propofol (14) and midazolam (15) were used to estimate residual propofol and midazolam effect-site concentrations at the time of ROR.

Evaluation of Response Surface Model Predictions

Model predictions were evaluated at two events: ROR after surgery and the first dose of analgesic (fentanyl) administered in the recovery room. For each model (a model based on end-tidal sevoflurane measurements and a model based on estimated effect-site sevoflurane concentrations), a prediction of OAA/S =1 ranging from 0 to 100% was made every 5 seconds from once the anesthetic was terminated to ten minutes after the time of each patient’s ROR. Model predictions were compared to observations with graphical and temporal analyses.

Graphical analysis

Predictions from each model were compared graphically on two plots: a prediction versus time plot and a plot of the remifentanil-sevoflurane concentrations at the time of emergence superimposed on a topographical representation of the response surface model predictions of OAA/S = 1. The topographical plot included the 5%, 50%, and 95% isoboles. Isoboles were defined as the set of remifentanil and sevoflurane concentration pairs that produced the same probability of effect. Mean model predictions recorded at ROR (OAA/S > 1) for the measured end-tidal sevoflurane and estimated sevoflurane effect-site based models were compared with an unpaired two-tailed t-test.

Empirical Cumulative Distribution

(16) Model predictions from each patient were sorted according to increasing probability. A percentage value was assigned to each patient as a percentage of all patients according to increasing probabilities. The patient population percentage was plotted versus the sorted model predictions. A uniform distribution of model predictions across patient percentage values from 0 to 100% was considered a good model fit.

Temporal Analysis

The time from the 50% model prediction probability of unresponsiveness to the time of observed ROR was calculated for each patient. Positive time differences indicated that patients emerged at model predictions of unresponsiveness less than 50% and the opposite for negative time differences. Time differences were reported as mean ± standard deviation. The time differences between the measured end-tidal sevoflurane and estimated sevoflurane effect-site based models were compared with an unpaired two-tailed t-test.

Similarly, two models of lack of response to 30 PSI of anterior tibia pressure algometry were evaluated at the time patients received their first dose of fentanyl in the recovery room: a model based on end-tidal sevoflurane measurements and a model based on estimated effect-site sevoflurane concentrations. For each model, a prediction of lack of responsive to 30 PSI of anterior tibial pressure ranging from 0 to 100% was made when patients received analgesic therapy (fentanyl) in the recovery room.

RESULTS

Section I: Response Surface Model Development for Application in Real Time

Sevoflurane-remifentanil interaction model parameters fit to responses previously recorded in volunteers are presented in Table 2.(2) Models include the probability of unresponsiveness (OAA/S = 1) and lack of response to 30 PSI of anterior tibial pressure. Two sets of models are presented: one using sevoflurane effect-site concentrations and the other using end-tidal sevoflurane concentrations. Coefficients of variation for estimates of remifentanil and sevoflurane C₅₀,’s, slope, and remifentanil-sevoflurane interaction (alpha) ranged between 8% and 149%.

Table 2.

Sevoflurane-remifentanil interaction model parameters fit to responses recorded in volunteers. Models include probability of unresponsiveness and lack of response to 30 PSI of anterior tibial pressure. Two sets of models are presented: one using sevoflurane effect-site concentrations and the other using end-tidal concentrations.

	Probability of unresponsiveness (OAA/S = 1)		Lack of response to Anterior Tibial Pressure (30 PSI)
Model Parameters	Effect-site	End-tidal	Effect-site	End-tidal
C50 Sevoflurane (vol %)	0.74 (8%)	0.78 (10%)	0.83 (12%)	0.89 (12%)
C50 Remifentanil (ng/mL)	50.9 (28%)	50.2 (30%)	1.3 (23%)	1.2 (24%)
Alpha (interaction)	9.4 (56%)	12.4 (61%)	0.9 (89%)	0.8 (94%)
N (slope)	5.2 (66%)	4.4 (93%)	2.7 (94%)	3.1 (149%)
Model Fit
% of Predictions >0.5 that matched observed responses	92%	93%	90%	90%
Spearman’s rho & P value	0.83 < 0.001	0.83 < 0.001	0.61 < 0.001	0.61 < 0.001

OAA/S indicates Observers Assessment of Alertness and Sedation(3). Model parameters were estimated using a Greco model structure. Numbers in parentheses represent coefficients of variation.

Using a probability of 0.5 or higher as a cutoff for model goodness of fit, the percentage of model predictions consistent with observed responses in volunteers were 90% or greater for all four models (Table 2). The Spearman Rank correlation coefficients for all models are presented in Table 2. The two-tailed t-test analysis rejected the null hypothesis that the revised models did not correlate with observations in volunteers.

Section II: Evaluation of Response Surface Models in Patients Undergoing Elective Surgery

All twenty patient subjects completed the study. Their American Society of Anesthesiologists Physical Status (PS) classification ranged from I to III. The height, weight, body mass index, and age were 173 ± 14 cm, 78 ± 18 kg, 26.3 ± 5.1 kg/m², and 45.4 ± 14.6 years respectively. Surgical procedures included open abdominal (eight) and laparoscopic (three), spine (four), head and neck (two), lower extremity vascular (one), and gynecologic (two) procedures. Estimated blood loss ranged from 0 to 7.5 mL/kg. Thirteen different surgeons and 8 different anesthesiologists participated in the study. The mean estimated effect-site concentrations at the time of emergence for the premedication dose of midazolam was 4.3 ± 2.2 ng/mL and for the induction dose of propofol was 0.1 ± 0.1 mcg/mL.

Evaluation of Response Surface Model Predictions

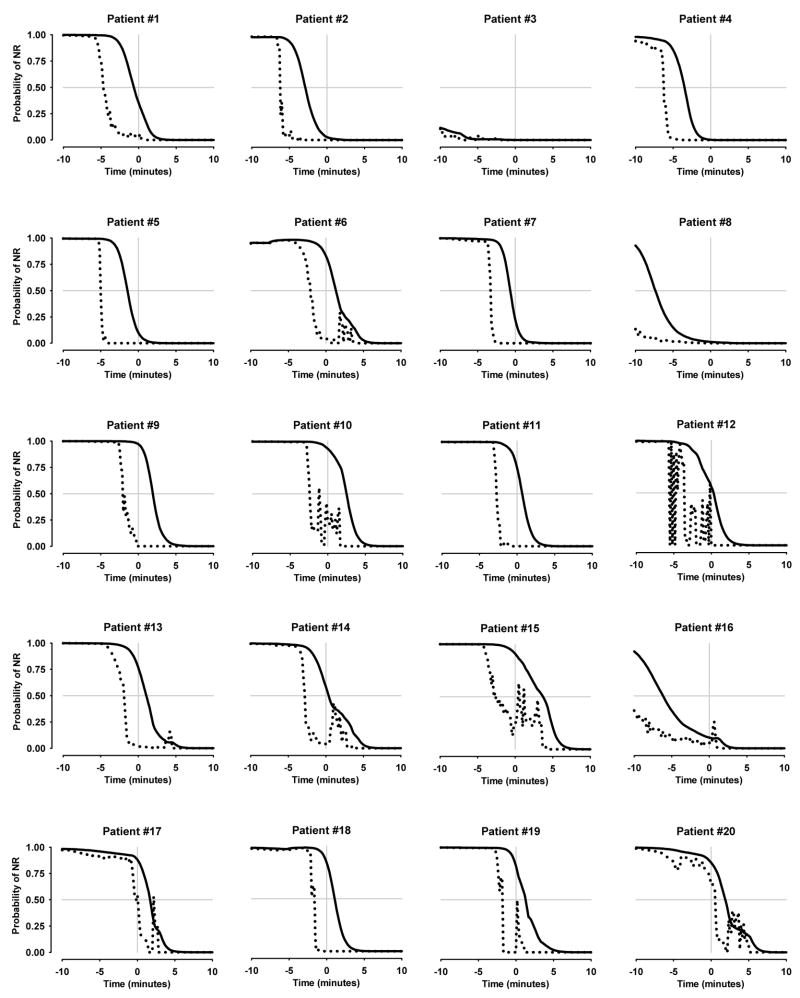
Figure 1 shows model predictions of OAA/S=1 over time during emergence from anesthesia for each patient. The rapid up and down changes in end-tidal based model predictions in selected patients (i.e. patient subject # 10, 12, 14, etc) were due to variations in respiratory function during emergence from anesthesia. The end-tidal concentration based model consistently predicted a high probability of ROR prior to the observed ROR. The effect-site concentration based model, by contrast, predicted high probabilities of ROR both before and after the observed ROR.

Figure 1.

Model predictions of return of responsiveness during emergence from anesthesia for each patient. The solid and dotted black lines show model predictions of OAA/S = 1 for the effect-site and the end-tidal based response surface models respectively. The gray vertical line represents the time at which each patient became responsive (OAA/S > 1). The x axis represents time ranging from 10 minutes before emergence to 10 minutes after. The solid gray horizontal line represents the 50% model probability of OAA/S = 1. NR indicates no response.

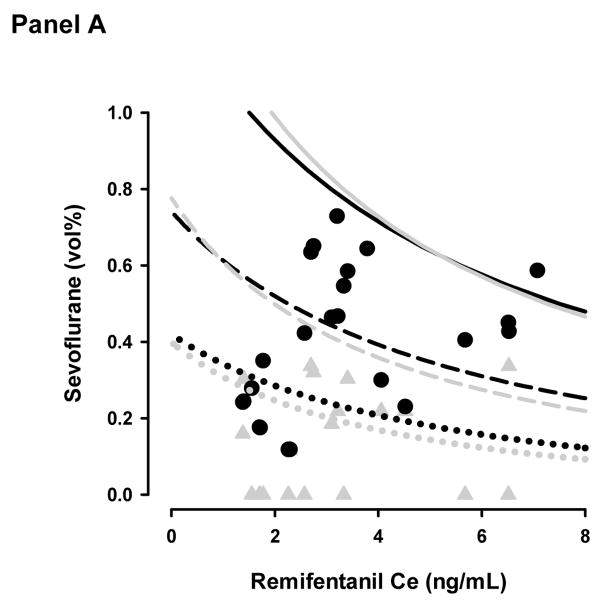
Figure 2a shows the sevoflurane - remifentanil concentration pairs at the time of emergence superimposed on a topographical representation of the model prediction a OAA/S=1. Concentrations are nearly equally distributed above and below the 50% isobole (8 below and 12 above) for the sevoflurane effect-site model and predominantly below the 50% isobole (19 below and 1 above) for the end-tidal model. At the time patients responded to voice command or prodding, the mean end-tidal sevoflurane concentration was 0.13 ± 0.13 vol%, predicted sevoflurane effect-site concentration was 0.44 ± 0.17 vol%, and remifentanil equivalent effect-site concentration was 3.5 ± 1.7 ng/mL. The average predicted probability of response was 53 ± 37% and 9 ± 19% for the effect-site and end-tidal models respectively (p < 0.001).

Figure 2.

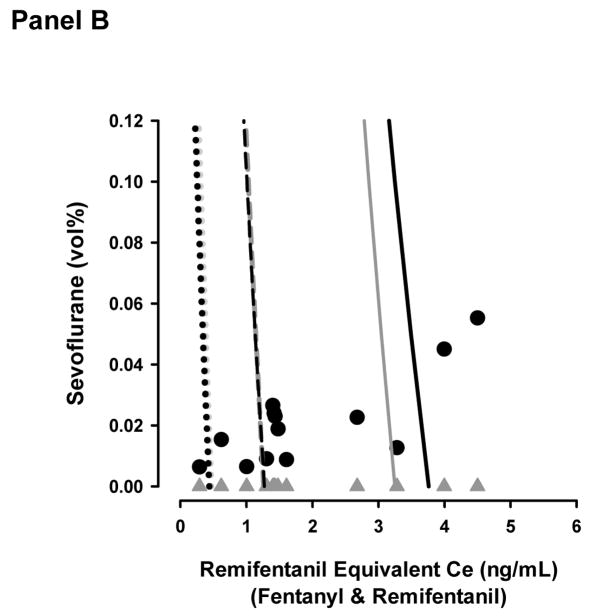
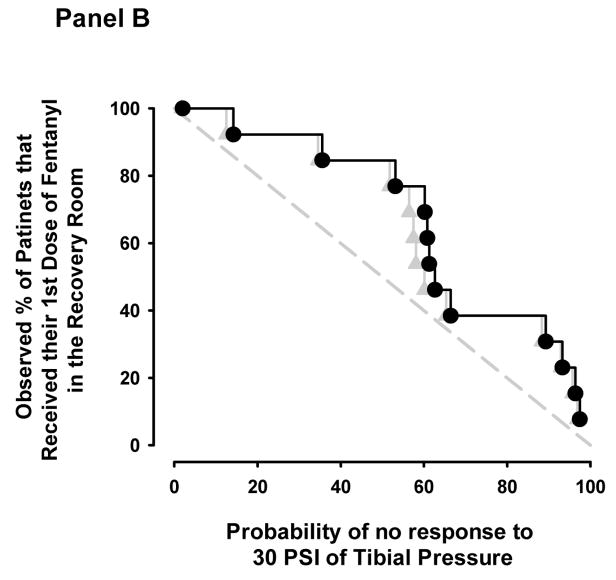
Topographical plots of model predictions of OAA/S = 1 (Panel A) and lack of response to 30 pounds per square inch of tibial pressure (Panel B). The dotted, dashed, and solid lines represent the 5%, 50%, and 95% model probabilities for the effect-site (black lines) and end-tidal (grey lines) models. The black circles and grey triangles represent the remifentanil-sevoflurane concentration pairs where patients emerged from anesthesia (Panel A) or required additional analgesia in the recovery room (Panel B) for the effect-site and end-tidal models respectively.

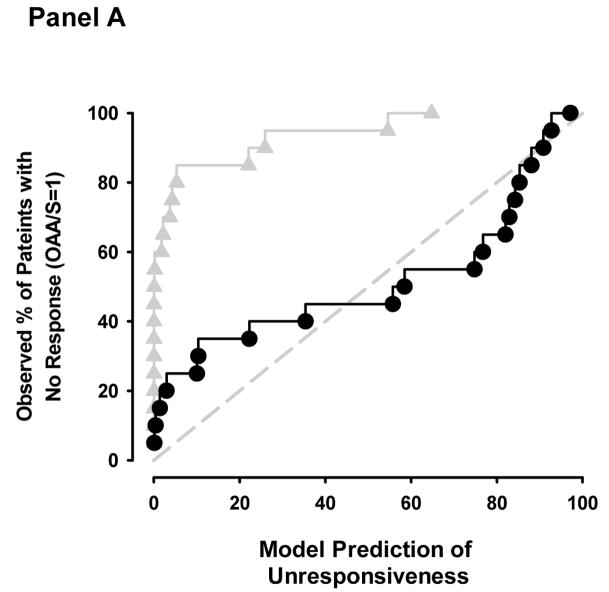
The empirical cumulative distribution plot illustrates the poor distribution of predictions across the patient percentage values for the end-tidal model (Figure 3a). For example, at the 20^th patient percentile, ideally 4 of the model predictions should be between 0 and 20% and the remainder of the predictions should be above 20%. At the 20^th percentile for the end-tidal model, 16 patients were between 0 and 20%. By contrast, the effect-site model had a more uniform distribution of predictions across patient percentage values, but the distribution was weighted at low and high predictions. For example, at the 50^th patient percentile, 7 of the model predictions were below 30% and 10 of the model predictions were above 70%.

Figure 3.

Cumulative distribution plots of model predictions of OAA/S = 1 when patients emerged from anesthesia (Panel A) and of lack of response to 30 pounds per square inch of tibial pressure just prior to when patients received their first dose of fentanyl in the recovery room (Panel B). The black circles and grey triangles represent the model prediction (vertical axis) and patient percentile ranking (horizontal axis) for remifentanil-sevoflurane concentration pairs for the effect-site and end-tidal models respectively.

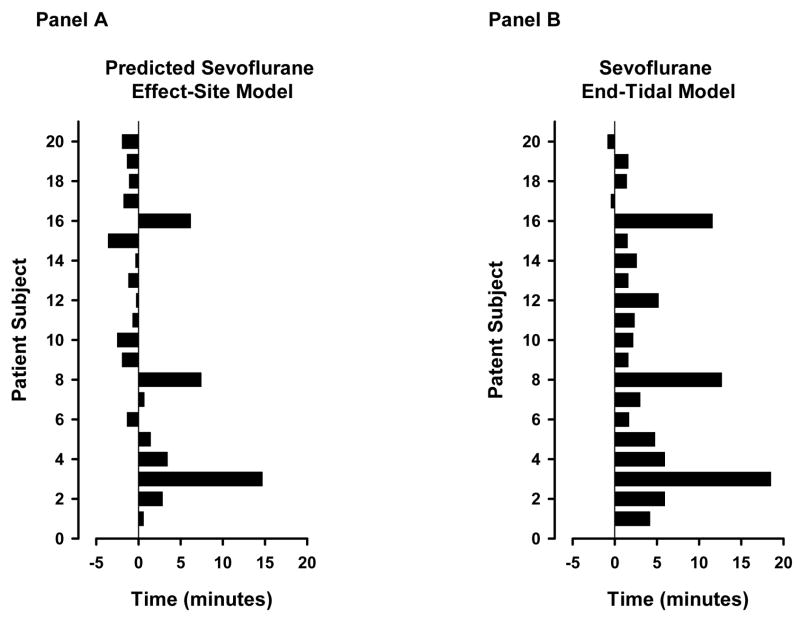
The mean time from the termination of the anesthetic until patient’s emerged from anesthesia was 5.3 ± 6.1 minutes. Patients emerged from anesthesia 0.9 ± 4.3 minutes after the effect-site based model predicted a 50% probability of unresponsiveness and 4.1 ± 4.9 minutes after the end-tidal based model predicted a 50% probability of unresponsiveness (p = 0.02, Figure 4).

Figure 4.

Time from the 50% model prediction for unresponsiveness to the time of the observed return of responsiveness for the effect-site based (Panel A) and end-tidal based (Panel B) models. After termination of the anesthetic, the model predicted probability of unresponsiveness rapidly decreased over time. A negative, zero or positive number on the horizontal axis indicates that the observed return of responsiveness occurred prior to, exactly at, or after the 50% probability of unresponsiveness. The vertical axis represents each subject.

Figure 2b shows the 5, 50, and 95% probability isoboles for the two models and the sevoflurane-remifentanil equivalent concentrations pairs when patients received their first dose of fentanyl during the first 30 minutes following surgery. Seven of the 20 patients did not require fentanyl during this time period. Concentration pairs are distributed predominantly above the 50% isobole for the effect-site based and end-tidal based models (3 below and 10 above). At the time of first fentanyl request for the management of post operative pain, the average end-tidal sevoflurane was 0.00 ± 0.00 vol%, predicted sevoflurane effect-site was 0.02 ± 0.01 vol%, and remifentanil equivalent effect-site concentration was 1.9 ± 1.3 ng/mL. The mean probabilities of no response to 30 PSI of anterior tibial pressure at the time patient’s required additional fentanyl were 61 ± 30% and 59 ± 30% for the effect-site and end-tidal models respectively (p = 0.893).

The empirical cumulative distribution plot illustrates a similar distribution of predictions across patient percentage values for both the end-tidal and effect-site models (Figure 3b). At the 50^th patient percentile, 6 of the model predictions were below 50% and 7 of the model predictions were above 50% for both models.

DISCUSSION

Section I: Response Surface Model Development

Revised models using the Greco model structure fit responses from volunteers reasonably well according to the comparison of prediction probabilities to observed responses. The Spearman Rank correlation coefficients for the probability of unresponsiveness models had stronger correlations with observations than the lack of response to pressure algometry models. There was no appreciable difference in model fit between the sevoflurane effect-site and end-tidal based models. This suggests that the original experiment was conducted at near steady-state conditions because a parameter to adjust for disequilibrium between end-tidal and effect-site sevoflurane concentrations did not appreciably alter the interaction parameters.

In comparison to prior studies, there is large variability between our work and previously published remifentanil C₅₀’s for predictions of OAA/S = 1.(2,17) One explanation may be that the remifentanil C₅₀ Greco model parameter is estimated from a data set where the majority of observations were made below the remifentanil C₅₀ = 50.9 ng/mL.

Section II: Evaluation of Response Surface Models in Patients Undergoing Elective Surgery

In this study, we conducted a preliminary evaluation of previously developed models of unresponsiveness and lack of response to a moderately painful stimulus (tibial pressure) in patients undergoing elective surgery. One study aim was to evaluate how well these models predicted emergence from anesthesia and the need for additional opioid in the recovery room.

While patients were anesthetized, model predictions indicated a high likelihood that patients would be unresponsive. With the probability of unresponsiveness models, predictions greater than 99% were consistent with observations (no patients demonstrated responsiveness). However, following termination of the anesthetic, model predictions of unresponsiveness rapidly decreased (Figure 1) and individual patients emerged from anesthesia over a wide spectrum of model predictions ranging from 1 to 97%. It is difficult to comment on the ability of these models to discriminate between awake or asleep during time intervals that are of clinical interest and how well the model predictions are calibrated to observations. The statistical tools that would be used to help answer these questions require a study with substantially larger sample sizes.

A second study aim was to evaluate the value of accounting for the lag time between end-tidal and brain sevoflurane concentrations during non steady-state conditions on model predictions. Model predictions using effect-site sevoflurane concentrations more adequately predicted ROR in patients emerging from anesthesia than model predictions using end-tidal sevoflurane concentrations. As illustrated in Figures 1 and 4, the model predictions of OAA/S = 1 using end-tidal sevoflurane levels typically predicted ROR prior to emergence. This model mis-specification is likely due to the biophase between end-tidal and effect-site sevoflurane concentrations during emergence. This was confirmed by the differences in mean predictions of emergence and mean time intervals between observed and predicted emergence between the two models. The improvement was also visualized in the topographical representation of the model predictions of OAA/S = 1 (Figure 2a). Ideal model predictions would be equally distributed about the 50% isobole. The concentration pair predictions are more equally distributed around the 50% isobole for the effect-site model but not the end-site model.

The benefit of using effect-site concentrations, however, was not as useful in model predictions in the recovery room. The end-tidal and effect-site model predictions of a lack of response to tibial pressure at the time when additional analgesic was required were similar (Figure 2b). Mean model probabilities were skewed above the 50% isobole (61 and 59%) predicting a lack of response to anterior tibial pressure in a majority of patients. This suggests that using 30 PSI may be a slightly less painful surrogate of pain encountered in the recovery room (an ideal distribution would be about the 50% isobole). Because sevoflurane levels were negligible, both models collapsed to a single drug (remifentanil equivalents) pharmacodynamic model. This is the most likely explanation for similar predictions between models (i.e. the sevoflurane concentrations are so low, they are nearly irrelevant in the recovery room in terms of analgesia).

These results in the recovery room, although promising, are difficult to interpret given the narrow spectrum of patients evaluated. We did not control for duration, type, or extent of surgery, use of local infiltration into the surgical site, and patient age. These factors and others may play a role in how patients respond to assessments of perceived pain in the recovery room.

Limitations

Several assumptions were made in implementing the Lerou model to predict sevoflurane effect-site concentrations. Cardiac output was normalized to weight but assumed to be constant (Appendix 1) and did not account for changes in cardiac output with induction of anesthesia, blood loss, etc. Cerebral blood flow was also assumed constant (16% of total cardiac output) and did not account for changes in PaCO₂. This could be especially important during emergence from anesthesia where changes in cardiac output and PaCO₂ with hyperventilation or permissive apnea could potentially change the time to return of responsiveness.(18) Future work directed at continuously updating model estimates of cerebral blood flow may improve accuracy of sevoflurane effect-site predictions.

In addition, we used the OAA/S score to build a response surface that predicts the probability of unresponsiveness. In the volunteer study, the OAA/S assessments were done in the absence of ongoing pain and without an endotracheal tube in place. We used this model to predict emergence from general anesthesia in patients whose tracheas were intubated following surgeries associated with mild to moderate surgical pain. No volunteer study can fully emulate the complexities of the clinical environment. The differences between the volunteer study on which the models are based and the clinical environment in which the models are applied likely impacts model performance to some degree.

Premedication with midazolam and induction with propofol may have prolonged emergence beyond model predictions but their contribution was most likely small. For example, midazolam levels were just below the C₅₀ for a Ramsay score of 2 (patient cooperative, oriented, and tranquil - 5.7 ng/mL) and well below the C₅₀ for a Ramsay score of 3 (patient sedated but responds to commands −71 ng/mL),(8) Propofol levels also were well below the C₅₀ for loss of responsiveness (2.2 mcg/mL)(1,17) making its contribution to prolonging emergence negligible.

In conclusion, predicted effect-site concentrations are commonly used to guide the delivery of intravenous anesthetics using target controlled delivery systems.(19) Extension of this concept to inhalation agents and to drug-drug interaction models may have value in guiding the delivery of anesthetics in combination by predicting the likelihood of adequate sedation, analgesia, and the time to emergence. In fact, clinical pharmacology display systems that apply these concepts and models in real time are currently under development.(20,21)

Table of inhalation agent pharmacokinetic model parameters.

Description	Abbreviation	Typical Value(Adjustment for Age, Weight, & Height)
Cardiac Output	Q	0.2 * wt0.75
Pulmonary Blood Flow	Qpulmt	0.95 * Q
Alveolar	QAlveolar
Intrapulmonary Shunt	QShunt	0.05 * Q
Systemic Blood Flow
Visceral Organ Blood Flow
Heart	QHeart	0.05 * Q
Brain	QBrain	0.160 * Q
Kidneys	QKidney	0.25 * Q
Liver	QLiver	0.3 * Q
Lean Organ Blood Flow
Muscles	QMuscle	0.13 * Q
Connective tissue	QConn	0.06 * Q
Adipose Blood Flow	QAdipose	0.05 * Q
Systemic Tissue Volumes
Visceral Organs
Total Body Vol	VBodyTotal	Weight
Heart	VHeart	0.004 * VBodyTotal
Brain	VBrain	0.0021 * VBodyTotal
Kidney	VKidney	0.004 * VBodyTotal
Liver	VLiver	0.057 * VBodyTotal
Lean Tissue
Muscle	VMuscle	0.426 * VBodyTotal
Connective tissue	VConn	0.260 * VBodyTotal
Adipose Tissue	VAdipose	0.150 * VBodyTotal
Blood Volume Compartments
Total	Vtotal	0.07 * Weightt
Arterial pool	VArterial	0.2 * Vtotal
Venous pool in adipose tissue	VAdipose	0.009 * Vtotal
Venous pool in lean tissue	VLean	0.291 * Vtotal
Venous pool in viscera	VViscera	0.319 * Vtotal
Central venous pool	VCV	0.101 * Vtotal
Partition Coefficients
Blood:Gas	λBlood:Gas	0.69
Kidney	λKidney	1.2
Heart	λHeart	1.7
Brain	λBrajn	1.7
Liver	λLiver	0.8
Muscle	λMuscle	3.1
Connective	λConnective	1.5
Adipose	λAdipose	48.0

Appendix 1. Pharmacokinetic model development used to predict sevoflurane effect-site concentrations

A multi-compartment pharmacokinetic model of inhalation agents developed by Lerou et al(4,5) was used to estimate effect-site concentrations from end-tidal levels. The Lerou model uses fresh gas flow, minute volume, vaporizer settings to predict inhalation agent end-tidal concentrations. In this analysis, the Lerou model was modified to use measured end-tidal concentrations instead of predicted ones as input. The model used Kennedy’s partition coefficients for sevoflurane (22) presented in the table below. Cardiac output, organ blood flow (to include cerebral blood flow), tissue volumes, blood pool compartments, carbon dioxide production, and oxygen uptake were normalized to patient weight and considered constant (23). Brain concentrations were defined as the blood concentration in the brain multiplied by the brain-blood partition coefficient. Effect-site concentrations represent the brain tissue concentrations scaled to end-tidal concentrations and were defined as brain tissue concentrations divided by the product of brain tissue blood partition coefficient and the blood gas partition coefficient.

Pharmacokinetic model development used the following steps:

1. Assumptions

   • alveolar concentrations ≈ end-tidal concentrations

     $$c{(t)}_{\mathit{alveolar}}=c{(t)}_{et}$$

   • Total blood volume is proportional to patient weight in kilograms

     $$V_{\mathit{blood}}=0.07\ast \mathit{weight}$$

   • Cardiac Output is dependent on patient weight

     $$Q(t)=0.2\ast \mathit{weigh}{t}^{0.75}$$

2. Compute the change of inhaled agent concentration in the arterial pool

   $$\frac{\mathrm{\Delta }c{(t)}_{\mathit{arterial}}}{\mathrm{\Delta }t}=\frac{Q(t)}{V_{\mathit{blood}\_\mathit{arterial}}}·\left({\lambda }_{\mathit{bloodgas}}·c{(t)}_{\mathit{alveolar}}·(1-\mathit{shunt})+\left(\mathit{shunt}·c{(t)}_{\mathit{venous}}\right)-c{(t)}_{\mathit{arterial}}\right)$$

3. Compute the change of volatile agent concentration in each tissue compartment over an iteration Δt

   $$\frac{\mathrm{\Delta }c{(t)}_i}{\mathrm{\Delta }t}=\sum _i\frac{Q{(t)}_i\left(c{(t)}_{\mathit{arterial}}-c{(t)}_i\right)}{V_i·{\lambda }_i},$$

   where i= {kidney, heart, brain, liver, muscle, connective, adipose}

4. Compute the change of concentration in the venous pool of viscera tissues

   $$\begin{array}{l}c{(t)}_{\mathit{viscera}}=\sum _j\frac{c{(t)}_j·Q{(t)}_j}{\sum _{j}Q{(t)}_j}\\ \frac{\mathrm{\Delta }c{(t)}_{\mathit{viscera}\_\mathit{out}}}{\mathrm{\Delta }t}=\frac{\sum _{j}Q{(t)}_j}{V_{\mathit{blood}\_\mathit{viscera}}}\left(c{(t)}_{\mathit{viscera}}-c{(t)}_{\mathit{viscera}\_\mathit{out}}\right),\end{array}$$

   where j = {kidney, heart, brain, liver} and V_{blood_viscera} = • 0.319 V_{blood_total.}

5. Compute the change of concentration in the venous pool of lean tissues

   $$\begin{array}{l}c{(t)}_{\mathit{lean}}={\displaystyle \sum _k}\frac{c{(t)}_k·Q{(t)}_k}{{\displaystyle \sum _k}Q{(t)}_k}\\ \frac{\mathrm{\Delta }c{(t)}_{\mathit{lean}\_\mathit{out}}}{\mathrm{\Delta }t}=\frac{{\displaystyle \sum _k}Q{(t)}_k}{V_{\mathit{blood}\_\mathit{lean}}}\left(c{(t)}_{\mathit{lean}}-c{(t)}_{\mathit{lean}\_\mathit{out}}\right),\end{array}$$

   where k = {muscle, connective} and V_{blood_lean} = 0.291 • V_{blood_total.}

6. Compute the change of concentration in the venous pool of adipose tissue

   $$\frac{\mathrm{\Delta }c{(t)}_{\mathit{adipose}\_\mathit{out}}}{\mathrm{\Delta }t}=\frac{Q{(t)}_{\mathit{adipose}}}{V_{\mathit{blood}\_\mathit{adipose}}}\left(c{(t)}_{\mathit{adipose}}-c{(t)}_{\mathit{adipose}\_\mathit{out}}\right),$$

   where V_{blood_adipose} = 0.009 • V_{blood_total.}

7. Determine the change of concentration in the central venous compartment

   $$\begin{array}{l}c{(t)}_{\mathit{venous}\_\mathit{out}}=\frac{c{(t)}_{\mathit{viscera}\_\mathit{out}}·{\displaystyle \sum _j}Q{(t)}_j+c{(t)}_{\mathit{lean}\_\mathit{out}}·{\displaystyle \sum _k}Q{(t)}_k+c{(t)}_{\mathit{adipose}\_\mathit{out}}·Q{(t)}_{\mathit{adipose}}}{Q(t)}\\ \frac{\mathrm{\Delta }c{(t)}_{\mathit{venous}}}{\mathrm{\Delta }t}=\frac{Q(t)}{V_{\mathit{blood}\_\mathit{venous}}}\left(c{(t)}_{\mathit{venous}\_\mathit{out}}-c{(t)}_{\mathit{venous}}\right),\end{array}$$

   where j = {kidney, heart, brain, liver}, k = {muscle, connective}, and V_{blood_venous} = 0.101 •V_{blood_total.}

8. Update the compartmental concentrations for iteration (t+Δt)

   $$\begin{array}{l}c{(t+\mathrm{\Delta }t)}_{\mathit{arterial}}=c{(t)}_{\mathit{arterial}}+\frac{\mathrm{\Delta }c{(t)}_{\mathit{arterial}}}{\mathrm{\Delta }t}c{(t+\mathrm{\Delta }t)}_{\mathit{viscera}\_\mathit{out}}=c{(t)}_{\mathit{viscera}\_\mathit{out}}+\frac{\mathrm{\Delta }c{(t)}_{\mathit{viscera}\_\mathit{out}}}{\mathrm{\Delta }t}\\ c{(t+\mathrm{\Delta }t)}_{\mathit{lean}\_\mathit{out}}=c{(t)}_{\mathit{lean}\_\mathit{out}}+\frac{\mathrm{\Delta }c{(t)}_{\mathit{lean}\_\mathit{out}}}{\mathrm{\Delta }t}\\ c{(t+\mathrm{\Delta }t)}_{\mathit{adipose}\_\mathit{out}}=c{(t)}_{\mathit{adipose}\_\mathit{out}}+\frac{\mathrm{\Delta }c{(t)}_{\mathit{adipose}\_\mathit{out}}}{\mathrm{\Delta }t}\\ c{(t+\mathrm{\Delta }t)}_{\mathit{venous}}=c{(t)}_{\mathit{venous}}+\frac{\mathrm{\Delta }c{(t)}_{\mathit{venous}}}{\mathrm{\Delta }t}\end{array}$$

9. Determine effect-site concentration c(t+Δt) _eff. Note that in the equation below c(t)_brain is the brain blood concentration (i.e. the brain tissue concentration divided by the brain tissue blood partition coefficient).

   $$c{(t+\mathrm{\Delta }t)}_{\mathit{eff}}=\frac{c{(t)}_{\mathit{brain}}}{{\lambda }_{\mathit{bloodgas}}}$$