Fe L-edge XAS of Low Spin Heme Relative to Non-heme Fe Complexes: Delocalization of Fe d electrons into the Porphyrin Ligand

Abstract

Hemes (iron porphyrins) are involved in a range of functions in biology including electron transfer, small molecule binding and transport, and O₂ activation. The delocalization of the Fe d-electrons into the porphyrin ring and its effect on the redox chemistry and reactivity of these systems has been difficult to study by optical spectroscopies due to the dominant porphyrin π → π* transitions which obscure the metal center. Recently we have developed a methodology that allows for the interpretation of the multiplet structure of Fe L-edges in terms of differential orbital covalency (i.e. differences in mixing of the d-orbitals with ligand orbitals) using a valence bond configuration interaction (VBCI) model. Applied to low spin heme systems, this methodology allows experimental determination of the delocalization of the Fe d-electrons into the porphyrin (p) ring both in terms of P→Fe σ and π donation and Fe→P π back-bonding. We find that π donation to Fe(III) is much larger than π back-bonding from Fe(II), indicating that a hole super-exchange pathway dominates electron transfer. The implications of the results are also discussed in terms of the differences between heme and non-heme oxygen activation chemistry.

Introduction

Heme (iron porphyrin) sites are involved in a range of biological functions including electron transfer (e.g. cytochromes a, b, c and f)^1-3 which cycle between low-spin Fe(II) and low-spin Fe(III), small molecule binding and transport,^4,5 catalysis and O₂ activation (e.g. peroxidases and cytochromes P450)^6-11 where high valent Fe centers are involved in H atom abstraction, hydroxylation and epoxide formation. Heme sites are fundamentally different from non-heme iron sites in that the porphyrin ligand allows for the delocalization of the iron d electrons into the porphyrin π system.^12-14 This changes the nature of the Fe in terms of the flexibility of the central coordination site, the energetics of reactivity, and its function in electron transfer (ET).¹¹

Heme enzymes have been easier to study than non-heme Fe enzymes because of the intense characteristic porphyrin π → π* transitions. However, these transitions have made studying the metal center difficult because they obscure many of the spectral properties of the Fe sites. A good example of this difficulty is reflected in the differences in understanding of the Fe sites in two classes of O₂ transport proteins, hemerythrin^15,16 (non-heme) and hemoglobin^17-19 (heme). The binuclear Fe site of oxy-hemerythrin can be clearly assigned as a hydroperoxide bound to a binuclear Fe(III) center by a range of spectroscopies.^15,16 In contrast, there has been significant controversy over the assignment of the electron distribution between the Fe and the O₂ in oxyhemoglobin.^4,20-28

Spectroscopic methods that have been used to probe the electron distribution in the d-orbitals of ferro- and ferriheme systems include NMR,^29,30 EPR and Mössbauer.^31-33 In systems with a low spin Fe(III) center, EPR is able to probe the energy splitting of the d_xy, d_xz, d_yz orbitals,^34,35 and can thus provide insight into the π donation of the heme center compared to that of axial ligands.^36-38 While significant insight can be obtained using EPR spectroscopy, the interpretation of the g values in terms of orbital energies is complicated due to the effects of covalency on the spin-orbital coupling.³⁹ While EPR or Mössbauer spectroscopy⁴⁰ can provide an assignment of the splitting patterns of the d_π orbital set, there is still no direct probe of the relative effects of covalency and ligand field. The NMR spectra of low-spin Fe(III) provide evidence for significant π donation from the porphyrin ring to the Fe, and evidence for little back-bonding.^29,30,41,42 No spectroscopic approach has simultaneously provided substantial information about the bonding and back-bonding in low spin Fe(II) porphyrins. These interactions in both redox states are of key importance in identifying ET pathways in the cytochromes, and contribute directly to O₂ activation in a number of heme enzymes.

Fe L-edge x-ray absorption spectroscopy (XAS) provides a number of key probes of bonding that are not available using other experimental techniques. An L-edge is composed of an L₁ edge, 2s→3d transition, and the L_2,3 edges, the 2p→3d transition split by final state spin –orbit coupling into the ²P_3/2(L₃) and the ²P_1/2(L₂) edges. The first of these edges (L₁) is electric dipole forbidden and as a consequence has very little intensity compared to the L_2,3 edges which are electric dipole allowed and have greater intensity. Thus, L-edge spectroscopy both generally and herein refers to transitions to the L_2,3 edge.^43,44 Given that the 2p orbital is localized on the Fe, Fe L_2,3-edge intensity is directly proportional to the Fe d-character in the unoccupied valence orbitals of the metal.^45-48 In addition, the energy shift of the L-edge has contributions from Z_eff of the metal and the ligand field splitting of its d orbitals. Finally, the L-edge spectral shape is sensitive to both the ligand field and covalency (vide infra), but these are complicated by 2p⁵3d^N+1 multiplet effects similar to the effects described by the Tanabe Sugano⁴⁹ matrices and diagrams for d^N ground states.^48,50

The sum of these contributions to the spectra can be calculated using the ligand field multiplet model implemented by Thole.⁵¹ In early versions of the model the effect of covalent delocalization on the L-edge was only accounted for by the reduction of the Slater integrals associated with electron repulsion, (by κ<0.8).^52-54 Later versions of the model included first, the effects of donor covalency through Ligand to Metal Charge Transfer (LMCT)⁵⁵ and later acceptor covalency through metal to ligand charge transfer (MLCT).^56-58 These models explicitly allowed each symmetry set of d^N and d^N+1L (where L=ligand hole) in the case of LMCT or d^N and d^N-1L^- (where L^- = ligand plus an electron) in the case of MLCT configurations to mix using a valence bond configuration interaction (VBCI) model. Recently, we have adapted the model to simultaneously include both the effects of LMCT (donor) and MLCT (back-bonding) on spectral shape.⁵⁰

A methodology has been developed,⁴⁸ based on multiplet simulations, that enables the determination of the covalent delocalization of the different symmetry sets of d-orbitals, called differential orbital covalency (DOC). The technique has been successfully applied to systems where both ligand to metal donation and metal to ligand back-bonding are present.^48,50 Herein, we examine the Fe L-edge spectra of low spin Fe(II) and Fe(III) heme compounds [Fe(tpp)(ImH)₂] and [Fe(tpp)(ImH)₂]Cl to experimentally determine the valence delocalization of the Fe d electrons into the porphyrin orbitals. These spectra are compared to those obtained from the low spin reference compounds [Fe(tacn)₂]Cl₂/Cl₃ with no π bonding, allowing a quantitative determination of the differences between heme and non-heme Fe site electronic structures that contribute to differences in reactivity.

Experimental

Samples

The compounds [Fe(tpp)(ImH)₂]Cl and [Fe(tpp)(ImH)₂] were synthesized according to published methods.^59-61 Samples were finely ground and spread across double-sided adhesive conductive graphite tape and attached to a copper paddle, aligned 45° to the incident beam as described previously.^48,62 These conditions result in isotropic L_2,3 edge spectra.

XAS data collection and reduction

X-ray absorption spectra were recorded at the Stanford Synchrotron Radiation Laboratory (SSRL) on the 31-pole wiggler beam line 10-1 under ring operating conditions of 50-100 mA and 3GeV. The radiation was dispersed using a spherical grating monochromator set at 1000 lines/mm and 20 μm entrance and exit slits (0.15 eV resolution). All measurements were made at 20±5°C. Sample measurement was performed using total electron yield mode where the sample signal (I₁) was collected with a Galileo 4716 channeltron electron multiplier aligned 45° relative to the copper paddle and 90° to the incident beam. The signal was flux normalized (I₁/I₀) by the photocurrent of a gold-grid reference monitor (I₀). Data for all samples were recorded in a sample chamber maintained at < 1 × 10^-5 Torr, isolated from the UHV beam line by a 1000 Å diamond window. The photon energy was calibrated from the Fe L-edge spectrum of powdered α-Fe₂O₃ (hematite) (<5 micron) run at intervals between scans. The second feature in the L₃ and the first feature in the L₂ edges were calibrated to 708.5 and 720.1 eV respectively. Data were taken over the range 670-830 eV to permit normalization as described previously.⁴⁸ A step size of 0.1 eV was used over the edge region (700-730 eV), and 0.5 eV steps over the remaining regions. The total scan took ~10 min, 4 mins over the region 700-730 eV. No photoreduction was observed during that time, in any of the samples described herein. A function of the form; absorption = [tan^-1(k (energy-I₁) +π/2)* 2/3* 1/π] + [tan^-1(k (energy -I₂) + π/2) *1/3 * 1/π] where k = 0.295 obtained by experimental fit^48,63 and I₂ = I₁+12.3eV (energy split by spin orbit coupling) was used to model the L₃- and L₂- edge jumps, as described previously.⁴⁸ The absolute energy of the arctangent was estimated based on a fit to the L-edge experiment. The L₃ intensity reported here is defined after normalization between 700 and 715 eV for [Fe(tacn)₂]Cl₂/[Fe(tpp)(ImH)₂], and 701 - 716 eV for [Fe(tacn)₃]Cl₃/[Fe(tpp)(ImH)₂]Cl, and the L₂ intensity is defined after normalization between 715 – 730 eV for [Fe(tacn)₂]Cl₂/[Fe(tpp)(ImH)₂] and 716 - 731 eV for [Fe(tacn)₂]Cl₃/[Fe(tpp)(ImH)₂]Cl. The error reported represents the range of integrated intensities based on at least three repeat measurements of the same Ligand field multiplet calculations were performed using the multiplet model implemented by Thole,⁵¹ the atomic theory developed by Cowan,⁶⁴ and the crystal field (i.e. symmetry) interactions by Butler.⁶⁵ This approach includes both electronic Coulomb interactions and spin-orbit coupling for each sub-shell.^56,66 To simulate the spectra, the Slater-Condon-Shortley parameters (F_i and G_i) were first reduced to 80% of their Hartree-Fock calculated values to account for the over-estimation of electron-electron repulsion found in calculations of the free ion, i.e (κ=0.8) in nomenclature used elsewhere.^56-58 The spectrum is calculated from the sum of all possible transitions for an electron excited from the 2p level into a 3d level.⁶⁷ In the ligand field limit the ground state is approximated by a single electronic configuration d^N split in energy by a crystal field potential in D_4h symmetry defined by the parameters Dq, Ds and Dt where the relationship between the orbital energies the crystal field parameters is b_1g(d_x2-y2) = 6Dq+2Ds-1Dt, a_1g(d_z2)= 6Dq-2Ds-6Dt, b_2g(d_xy) = -4Dq+2Ds-1Dt, e_g(d_xz/d_yz) = -4Dq-1Ds+4Dt.^66,68 To avoid confusion any time D_4h symmetry is used we will so indicate, for example by e_g(D_4h). Covalent mixing of the metal valence d orbitals with the ligand valence p orbitals is simulated using a charge transfer model which in the case of ligand to metal charge transfer (LMCT) adds a d^N+1L configuration above the d^N ground state. The d^N+1L configuration is set at an energy (Δ) above the d^N configuration and these two states are coupled by configuration interaction (CI), represented by the mixing term T_i = <3d^N|h|d^N+1L> where h is the molecular Hamiltonian and T_i is proportional to metal-ligand overlap for each of the i symmetry blocks. For a donor ligand system the ground and LMCT states are Ψ_GS,B = α₁|3d^N> + β₁|3d^N+1L> and Ψ_GS,AB = β₁|3d^N> - α₁|3d^N+1L> respectively, and the L-edge excited states are Ψ_ES,B = α₂|2p⁵3d^N+1> + β₂|2p⁵3d^N+2L> and Ψ_ES,AB = β₂|2p⁵3d^N+1> - α₂|2p⁵3d^N+2L>, where the coefficients α₁, α₂, β₁, β₂ are a function of T and Δ for the ground state and T and Δ’ for the excited state, where Δ’ = Δ+U-Q, and U is the 3d-3d electron repulsion and Q is the 2p-3d repulsion. Ligand field, T and Δ were allowed to vary in final state fits (i.e. decrease) but had little effect on the covalent mixing observed from the fits. Simulations showing the effects of varying final state T , Δ and Ligand Field parameters are given in Figure S9. In order to include back-bonding (MLCT) in addition to σ donation it is necessary to introduce a third state Δ_π above the d^N configuration; the ground state wave-function is now a linear combination of three configurations, 3d^N-1L^-, 3d^N and 3d^N+1L. Further technical details, and program input files for the three configuration simulations, including both LMCT and MLCT are given elsewhere.⁵⁰ spectrum on different dates.

Computational Details

To simulate the spectra, the effects of the different components of bonding were systematically evaluated. First, the effects of σ and π donation were included by ligand to metal charge transfer (LMCT) simulations; then the addition of π back-bonding to the porphryin and other effects, were systematically considered by including metal to ligand charge transfer (MLCT). Parameters that determine the energy separation in the ground state between the d^N-1L^-, d^N and d^N+1L configuration (Δ and Δ_π), were calculated from the program parameters (EG1/EG2/EG3)⁶⁹ and in the final state (Δ’ and Δ_π’) (EF1/EF2/EF3) were initially chosen based on previous results⁵⁰ then systematically varied to optimize the spectral fit.

In order to get the DOC, the projection method of reference ⁴⁸ was applied. This method uses the TT-multiplets program to split the intensity of the spectrum into its different symmetry components, via dummy transitions (4s→4p). These values are then degeneracy weighted to get the DOC.

DFT calculations

The starting structures of the two molecular complexes [Fe(tpp)(ImH)₂]⁺ and [Fe(tpp)(ImH)₂], were taken from the crystal structure of [Fe(tpp)(ImH)₂](Cl).(H₂O).(CHCl₃).⁶¹ Those of [Fe(tacn)₂]^3+/2+ were taken from the [Fe(tacn)₂]Cl₃.5H₂O^70,71 and [Fe(tacn)₂]Cl₂.4H₂O structures.⁷² In all cases the molecular structures of the Fe complexes were well isolated in the unit cell. DFT calculations (ground state) were performed using the ADF program.⁷³ The geometries were optimized using the exchange functional of Becke⁷⁴ and the correlation functional of Perdew (BP86), as implemented in ADF ⁷⁵ The frozen core approximation⁷⁶ was used for the iron 1s-2p orbitals. For valence orbitals, Slater-type orbital (STO) basis sets of triple-ζ quality were employed with polarization functions on the ligand atoms (3d) and additional valence p orbitals on the metal atoms. i.e. ADF basis set IV.^73,77 This basis set combination has been shown to give a well converged solution.^78,79 Calculations were also performed including implicit solvation, this was done using the COnductor-like Screening MOdel, (COSMO).^80-82 Non-bonded radii used (in Å) were: N = 1.608, H = 1.350, C = 1.700, O = 1.517 and Fe = 1.80. A dielectric constant of 78.8 (water) and an outer cavity radius of 1.9 Å were further used to parameterise the COSMO solvation cavity.^73,83 Solvation model orbital splitting patterns and mixing coefficients were found to be similar to those calculated using a gas-phase model. Ground state energies and eigenfunctions (Kohn-Sham orbitals) are used to correlate to data. Previous studies on molecular systems have shown reasonable empirical correlations between experimental d-d transitions and ground state d-orbital energy differences,^84-86 which also correlated to TD-DFT calculation results.⁸⁶ Core-hole effects on ligand field splittings using a cobalt atom with a nuclear charge of Fe have been evaluated elsewhere;^87,88 trends in ligand field effects between compounds were found to be largely unaffected by the presence of the core hole. Mulliken population analysis was performed as implemented in ADF.⁸⁹ Orbital plots were generated using G-OpenMol Version 2.2.⁹⁰

Results-Spectroscopy

A. Fe(II)

Figure 1a shows the normalized Fe L-edge spectrum of [Fe(tpp)(ImH)₂] compared to that of [Fe(tacn)₂]Cl₂ (taken from reference ⁴⁸). The Fe L-edge spectrum of [Fe(tpp)(ImH)₂] increases slightly in total intensity and shifts 0.7 eV to higher energy relative to the non-heme low spin Fe^II reference complex. The change in intensity corresponds to a change in the total metal d character in the unoccupied orbitals, which goes from 295±20% (non-heme) to 309±30% (heme), (Table 1).⁹¹ In systems without back-bonding higher d character in unoccupied orbitals indicates lower covalency, where covalency is defined as the amount of ligand character in the metal d orbitals. In systems where back-bonding is present there is also a covalency contribution arising from the mixing of occupied metal character into the unoccupied ligand orbitals which increases total intensity. When the spectra are scaled and superposed (Figure 1a, inset) we see an increase in intensity on both sides of the main multiplet packet indicated by the arrows in Figure 1.

Figure 1.

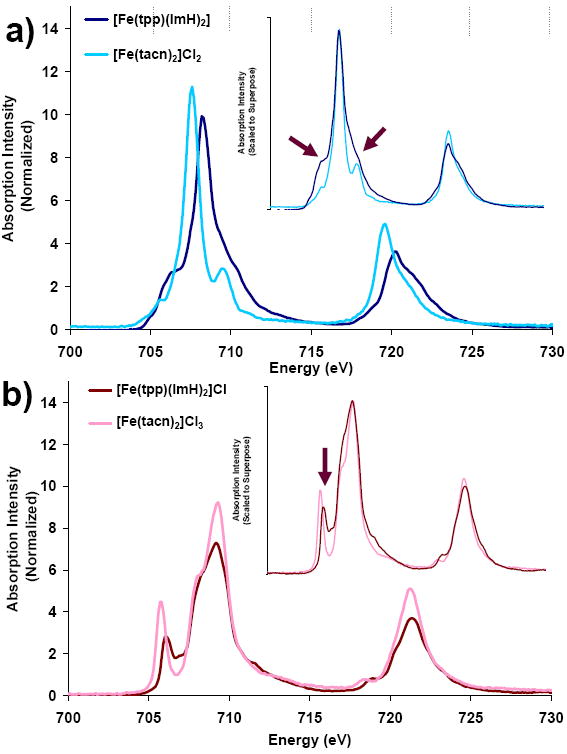
Fe L-edge comparison of heme and non-heme Fe compounds. a) [Fe(tacn)₂]Cl₂ and [Fe(tpp)(ImH)₂] b) [Fe(tacn)₂]Cl₃ and [Fe(tpp)(ImH)₂]Cl. Insets show spectra that have been intensity-scaled and energy-shifted to superimpose.

Table 1.

Summary of Fe L-edge experimental data for [Fe(tpp)(ImH)₂]Cl, [Fe(tacn)₂]Cl₃, [Fe(tpp)(ImH)₂] and [Fe(tacn₂)]Cl₂.

	Total Intensity	% Metal character summed over unoccupied orbitals†	% Average metal character in unoccupied orbitals†	L3 area	L2 area	Branching ratio L3/(L2+L3)	L3 intensity weighted edge energy center (eV)	L2 intensity weighted Edge energy center (eV)
[Fe(tacn)2]Cl3 FeIII non-heme48	43.8(3.5)	351(25)	70(5) As Fe(III)	29.6	15.9	0.67	709.0	721.4
[Fe(tpp)(ImH)2]Cl FeIII heme	38.3(2.5)	303(27)	61(6) As Fe(III)	26.3	12.0	0.69	708.9	721.3
[Fe(tacn)2]Cl2 FeII non-heme48	37.4(2.5)	295(20)	74(5) As Fe(II)	23.7	13.7	0.65	707.6	720.0
[Fe(tpp)(ImH)2] FeII heme	39(3.5)	309(30)	77(7) As Fe(II)	26.6	12.4	0.68	708.4	720.6

^†The % metal character summed over unoccupied orbitals reflects the combined effects of covalency and back-bonding. In a system with no back-bonding this number divided by the number of holes gives the % metal character in each orbital. For [Fe(tacn)₂]Cl₃, 351/5 =70 as given in column 3, line 1.

B. Fe(III)

Figure 1b shows the normalized Fe L-edge spectrum of [Fe(tpp)(ImH)₂]Cl compared to that of [Fe(tacn)₂]Cl₃, (from reference ⁴⁸). The Fe L-edge spectrum of the heme compound [Fe(tpp)(ImH)₂] decreases in total intensity and shifts slightly (0.1 eV) to lower energy relative to the low spin non-heme reference complex. The decrease in total intensity corresponds to a change in the valence metal character from 351±25% to 303±27%, (Table 1). The decrease in metal character of the low spin Fe(III) heme relative to the non-heme reference complex has two possible contributions: increase in net ligand donation and/or a decrease in back-bonding. This decrease in intensity is opposite to the small increase observed in the Fe(II) L-edges described above. When the spectra of [Fe(tacn)₂]Cl₃ and [Fe(tpp)(ImH)₂] are scaled and superimposed (Figure 1b, inset) the feature to lowest energy (assigned as a 2p transition to the (t_2g)⁵ O_h hole)⁴⁸ shifts closer in energy to the main feature and significantly decreases in intensity.

Results-DFT Calculations

The DFT calculations described here compare the bonding between heme and non-heme Fe systems, where the non-heme system chosen for comparison is iron complexed to two tacn ligands, shown in Scheme 1. Tacn (1,4,7 triazacyclononane) is a tridentate secondary amine chelate that interacts with a metal as a σ donor set with approximately O_h symmetry. In an O_h ligand field the Fe d orbitals split into the 2-fold degenerate e_g σ* set, and the 3-fold degenerate t_2g π_nb set. [Fe(tacn)₂]^2+/3+ has a trigonal distortion which further splits the metal t_2g orbitals into e_g(D_3d) and a_1g(D_3d) sets. The actual Fe site symmetry in the crystal is C₁^71,92 and the MO calculations on [Fe(tacn)₂]^2+/3+ compounds were performed in C₁ symmetry.

Scheme 1.

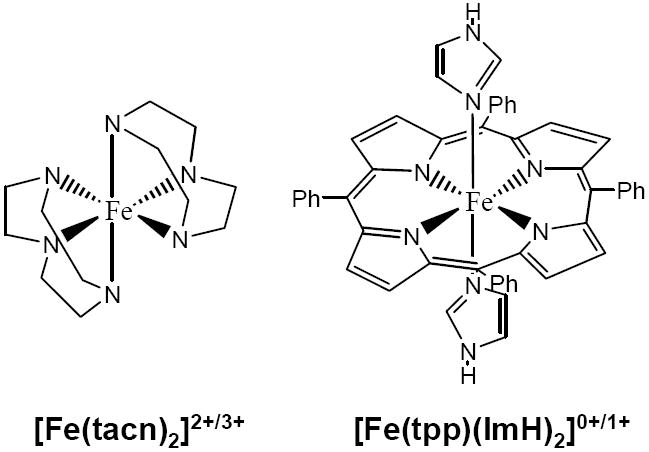
The heme ligand set studied here is comprised of the tetraphenylporphyrin (tpp) and two axial imidazoles (ImH). The effective symmetry of the heme complex, excluding the axial imidazoles and phenyl substituents, is D_4h. Under D_4h symmetry the heme ligand has two occupied orbitals capable of engaging in σ donor interactions with the Fe(3d) orbitals, one with b_1g(D_4h) symmetry which will interact with the metal d_x2-y2 orbital, and an orbital of a_1g(D_4h) symmetry which can interact with the metal d_z2 orbital. There are two additional sets of porphyrin orbitals which have a π interaction with the metal. The 3e_g(D_4h) porphyrin orbitals are occupied and act as π donors, while the 4e_g(D_4h) porphyrin orbitals are unoccupied and capable of acting as π acceptors. A MO diagram for two axial imidazoles oriented in an eclipsed configuration is given in Figure S2. A MO diagram for tpp (in C_i symmetry) is given in Figure S3. In this configuration orbital 12 of the axial ImH can act as a σ donor, orbitals 11 and 13 can act as π donors, and the orbital 14 (LUMO) can act as a π acceptor. When combined with a metal, this axial ligation produces a complex with C_i symmetry.

A. Fe(II)

Figure 2 shows the energy levels from spin restricted calculations of [Fe(tpp)(ImH)₂] (left) and [Fe(tacn)₂]²⁺ (right). Spin unrestricted calculations were also performed and converged to the same solutions. The decomposition of the orbitals into their respective fragments from Mulliken population analyses are given in Table 2 and Figure 2. The predominantly metal based orbitals are offset to the center and the predominantly ligand based π* orbitals are offset to the side.

Figure 2.

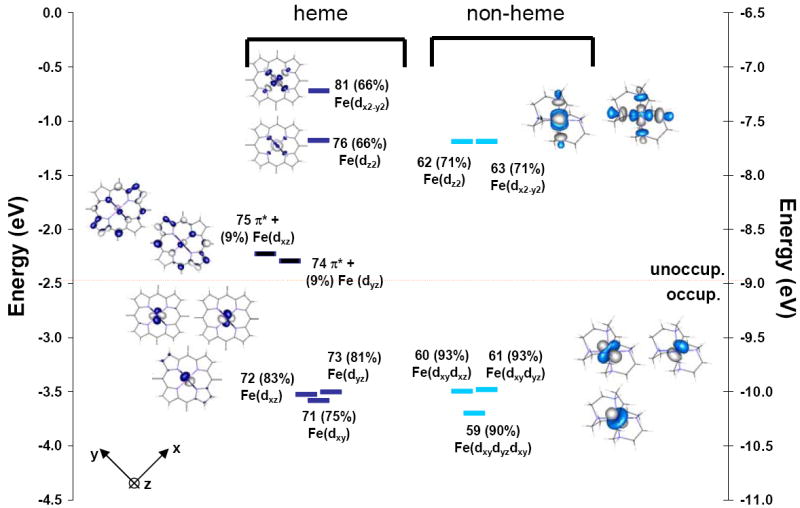
Comparison of energy levels for Fe(II) in a ferro-heme [Fe(tpp)(ImH)₂] and a non-heme [Fe(tacn)₂]²⁺ coordination. Orbitals are numbered as the output from ADF, calculations, with the % metal character in each orbital given in parentheses after the orbital number. Orbitals with metal character are fully colored. The predominantly porphyrin π* orbitals are colored in black. The main contributors to each MO of the compound [Fe(tpp)(ImH)₂] are given in Table 2 and in the Supporting Information, plots including the main porphyrin and ImH bonding orbitals are given in Figures S2 and S3.⁹⁴

Table 2.

Key orbital components for the DFT calculations of Fe(II)- [Fe(tpp)(ImH)₂] and Fe(III)- [Fe(tpp)(ImH)₂]⁺. MO diagrams of tpp and ImH are given in the Supporting Information, Figure S2 and S3. Bold numbers indicate the orbital number from the ADF calculation.

Main contribution to MO	Fe(II)-heme	Fe(III)-heme
Fe(dx2-y2)	81. 67%(Fe-dx2-y2) + 27%(6b2g-tpp) + 4%(tpp-other)	77. 61%(Fe-dx2-y2) + 29%(tpp-6b2g) + 6%(Fe-dz2).
Fe(dz2)	76. 65%(Fe-dz2) + 9%(tpp-a1g) + 2%(tpp-other)+ 18%(ImH-12) + 6%(ImH-other).	76. 59%(Fe-dz2) + 20%(ImH-12) + 8%(tpp-a1g) + 5%(Fe-dx2-y2)
Heme π-acceptor (4eg(D4h))	75. 90%(tpp-4eg) + 9%Fe(dyz/dxz)	75. 94%(tpp-4eg) + 6%(Fe-dyz) 74. 95%(tpp-4eg) + *3%(Fe-dxz)
Fe(dxz/dyz)	73. 81%(Fe-dxy+dxz) + 6%(tpp-4eg) + 2%(ImH-other)+ 5%(tpp-other) 72. 83%(Fe-dxy+dxz) + 7%(tpp-4eg) + 4%(tpp-other)	73. 70%(Fe-dyz) + 20%(tpp-3eg) + 2%(tpp-4eg) 3%(ImH-11) 72. 71%(Fe-dxz) + 22%(tpp-3eg) + 2%(tpp-4eg)
Fe(dxy)	71. 75%(Fe-dyz) + 15%(tpp-3eg) + 6%(tpp-4eg) + 5%(tpp-other)	71. 93%Fe(dxy)
Heme π-donor (3eg(D4h))	69. 56%(tpp-3eg) + 22%(tpp-52Ag) + 7%(Fe-dyz) + 11%(tpp-other) +7%(Fe-dxz/dyz/dxy)	64. 71%(tpp-3eg) + 19%(Fe-dyz)
Heme σ-donor (6b1g(D4h))**	60. 50%(tpp-6b2g) + 22%(Fe-dx2-y2) + 12%(tpp-41Ag) + 14%(tpp-other)+ 3%(ImH-other)	55. 36%(tpp-41ag) + 34%(tpp-6b2g) + 15%(Fe-dx2-y2) + 7%(tpp-45 Ag)
Heme σ-donor (7a1g(D4h))93	56. 33%(tpp-7a1g) + 22%(tpp-42ag) + 18%(Fe-dz2) + 18%(ImH-12ag) +5%(tpp-other)	52. 38%(tpp-7a1g) + 23%(Fe-dz2) + 15%(ImH-12ag) 50. 33%(tpp-42ag) 16%(tpp-40ag) + 16%(tpp-6b2g) + 10%(Fe-dx2-y2) + 2 %(Fe-dz2)

^**x and y axes bisect the N-Fe-N bonds.

When tacn interacts with Fe(II) the three orbitals to lower energy (59, 60 and 61) approximating the t_2g set in O_h symmetry, have mostly metal character (93%), and the two orbitals to higher energy (63 and 62), which are approximately the e_g(O_h) set split by the low symmetry ligand field, have decreased metal character (71%). Thus the tacn ligands form σ donor bonding interactions with the metal, but as expected do not have any substantial π interaction.

In the heme system, the five Fe d-orbitals split with two orbitals to higher energy (81 and 76), the e_g set in O_h, and three to lower energy (71, 72, 73), the t_2g(O_h) set (Figure 2). The d_x²-y² orbital (81) is at higher energy than the d_z2 orbital by about 1 eV (76), which indicates that the porphyrin is a better σ donor than the ImHs because d_z² has contributions from both the porphyrin a_1g(D_4h) and the ImH-12. Both the d_x2-y2 and the d_z² orbitals have 66% metal character, indicating that the heme ligand set is a stronger σ donor than the tacn ligand.

In low spin Fe(II) the metal based t_2g (in O_h) orbitals 72, 71 and 73 are occupied, thus their mixing with occupied ligand orbitals does not contribute any net bonding. However, the effects of back-bonding are evident (Figure 2) from both the metal character in the unoccupied porphyrin based 4_eg(D_4h) orbitals (9 %, 74 and 75), and the porphyrin 4_eg(D_4h) character (from a fragment analysis in ADF) mixed into the metal based d_xz and d_yz orbitals (9%, 72 and 73).

B. Fe(III)

Figure 3 shows the β-spin molecular orbitals from the spin-unrestricted DFT calculations for [Fe(tpp)(ImH)₂]⁺ (left) and [Fe(tacn)₂]³⁺ (right). As for Fe(II), orbitals that are predominantly metal-based are offset to the center of the diagram, with the porphyrin π* orbitals to the side. A more complete MO diagram including the σ and π donor orbitals that interact with the metal is given in the Supporting Information, Figure S5. The decomposition of the orbitals into their respective fragments using a Mulliken population analysis⁸⁹ is given in Table 2.

Figure 3.

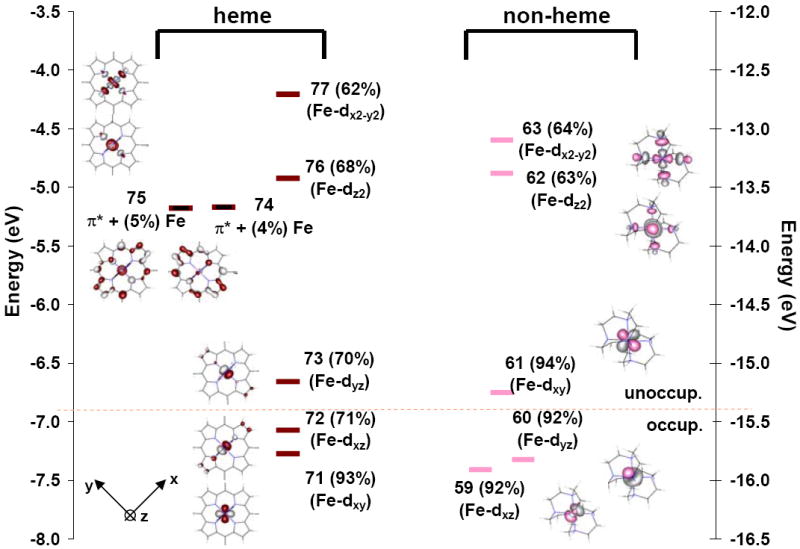
Comparison of the β-spin energy levels in Fe(III) heme vs non-heme: [Fe(tpp)(ImH)₂]⁺ orbitals are colored red and [Fe(tacn)₂]³⁺ orbitals are colored pink. Orbitals are numbered as the output from ADF calculations and the % metal character is given in parentheses after the number for each orbital. Orbitals with predominant metal character are fully colored. Those which have predominantly porphyrin (tpp) character are colored in black. The main contributors to each of the MOs of the compound [Fe(tpp)(ImH)₂] are given in Table 2 and in the Supporting Information.⁹⁴

As is the case for the Fe(II) systems, the σ donor interactions of the heme and non-heme ligand sets are calculated to be similar, by DFT calculations. The interaction with the porphyrin ligand results in the d_x2-y2 orbital having 62% metal character and the d_z² having 68% metal character. In comparison the non-heme tacn complex has 64% for both. In the heme ligand field the d_x²-y² orbital is about 1 eV higher in energy than the d_z² orbital, analogous to the Fe(II) heme calculation, which again indicates that the porphyrin is a stronger σ donor than the axial ImH ligand.

For the Fe(III) system the hole in the t_2g (O_h) d-orbital set allows for both the porphyrin and the axial ImH to potentially act as π-donors. When both ImH ligands are eclipsed and oriented along the z-axes with their molecular planes in the x,z plane where x is along an Fe-N bond; (Figure 3) this orientation allows their out-of-plane ImH π donor orbitals to interact with the Fe d_yz orbital, destabilizing it to become the β-spin LUMO. This orbital (73) contains 20% porphyrin π donor (3e_g) and 3% ImH π donor character (orbital 11), Table 2. The contribution of ImH character to the LUMO orbital is relatively small; however this interaction is sufficient to split the Fe d_xz/d_yz (72 and 73) orbitals in energy. Rotating the ImH planes out of the xz plane and staggering these orientations changes the coefficients of mixing with the two porphyrin 3e_g(D_4h) orbitals (vide infra).^30,41

The degree of π back-bonding from Fe(III) to the porphyrin can be assessed from the coefficients of the occupied metal orbital 72, (d_xz) and their relation to the unoccupied porphyrin 4e_g(D_4h) orbitals (since orbital 73 d_yz is unoccupied, its interaction with the porphyrin 4e_g orbital does not contribute to back-bonding). From Table 2 the metal character in the 4e_g(D_4h) π acceptor porphyrin orbitals decreases upon going from Fe(II) (9%) to Fe(III) (2%) indicating that in the DFT calculations there is very little back-bonding in the Fe(III) heme complex. This is consistent with NMR results for low-spin Fe(III) porphyrinates, which show undetectably small contact shifts at the meso-carbons of [PFeL₂]⁺ where L = imidazoles and high-basicity pyridines.^29,42

Analysis

1. L-edge intensity and energy: relative contributions of Z_eff and ligand field

Metal L-edge energy shifts are a consequence of three factors: the charge on the absorbing metal in the molecule, (Z_eff), ligand field splittings, and any difference in the nature of the transitions contributing to the spectra.⁵⁰

In non-heme Fe systems the ligand field contribution to the edge energy shifts can be estimated from optical 10Dq values.⁶² However, in heme systems 10Dq values are not known because the π → π* transitions obscure the metal d-d absorption bands.⁹⁵ From optical data the 10Dq values for [Fe(tacn)₂]²⁺ and [Fe(tacn)₂]³⁺ are 2.35 and 2.55 eV, respectively.^71,92,96 These compare well with the values from ground state DFT calculations of of 2.37 and 2.45 eV. Thus equivalent DFT calculations were used to estimate the d orbital energy splittings in the heme complexes giving for Fe(II), 10Dq = 2.86 eV, Ds = 0.056 eV and Dt = 0.047 eV and for Fe(III), 10Dq = 2.45 eV, Ds = 0.176 eV and Dt = 0.003eV where Ds and Dt are the ligand field parameters associated with the tetragonal distortion from O_h.⁶⁸

Fe(II)

The effect of Z_eff can be estimated from total L-edge intensity which reflects the total metal character in the unoccupied valence orbitals. In going from [Fe(tacn)₂]²⁺ to [Fe(tpp)(ImH)₂] the total intensity does not change significantly (Table 1), indicating that the effect of Z_eff on the energy shift is small. Ligand donation decreases intensity whereas back-bonding increases it. The small change in L-edge intensity indicates that heme σ donation of the porphyrin is sufficiently large to counteract any contribution due to the back-bonding in the heme complex. Based on the DFT calculated splittings of the d-orbitals, the L-edge spectrum of [Fe(tpp)(ImH)₂] should shift by ~0.3 eV to higher energy relative to that of [Fe(tacn)₂]Cl₂.⁹⁷ The observed experimental shift in the Fe L-edge is 0.7 eV. This difference could reflect an inadequate description by the ground state DFT calculations or an additional multiplet edge energy shift to higher energy due to MLCT transitions associated with back-bonding. The VBCI analysis described below indicates that this effect is largely ligand field based.

Fe(III)

Based on DFT calculations, the [Fe(tpp)(ImH)₂]⁺ spectrum would shift 0.1 eV to higher energy relative to that of [Fe(tacn)₂]²⁺. In comparing the L-edge spectra of [Fe(tacn)₂]Cl₃ to [Fe(tpp)(ImH)₂]Cl, a small decrease in total intensity is observed, indicating that Z_eff on the Fe atom has decreased, which would shift the spectrum to lower energy. The observed shift is close to zero, indicating that the ligand field counteracts the effect of Z_eff.

2. VBCI simulation of Fe(II) L-edge spectral shape: Differential Orbital Covalency and back-bonding

VBCI simulations of the spectra of the low spin Fe(II) complex were performed in D_4h symmetry. The simulations systematically included first, σ and π donation (ligand to metal charge transfer), second, solely π back-bonding (metal to ligand charge transfer) and finally, all bonding contributions.

2.1. Multiplet simulation: σ and π donation

Figure 4 shows three spectra: blue, the experimental spectrum of [Fe(tpp)(ImH)₂]; light grey, a pure d⁶ ground state split by a ligand field 90% of that predicted from the DFT calculations described above (similar to the [Fe(tacn)₂]Cl₂ spectrum),⁴⁸ and a dark grey spectrum that shows the effects of adding σ and π donation to the pale grey spectrum. It is clear from the figure that neither of these simulations fits the data. The addition of σ and π donation act to sharpen the spectrum, not broaden it, as required to fit the experimental L-edge spectrum of the heme site.

Figure 4.

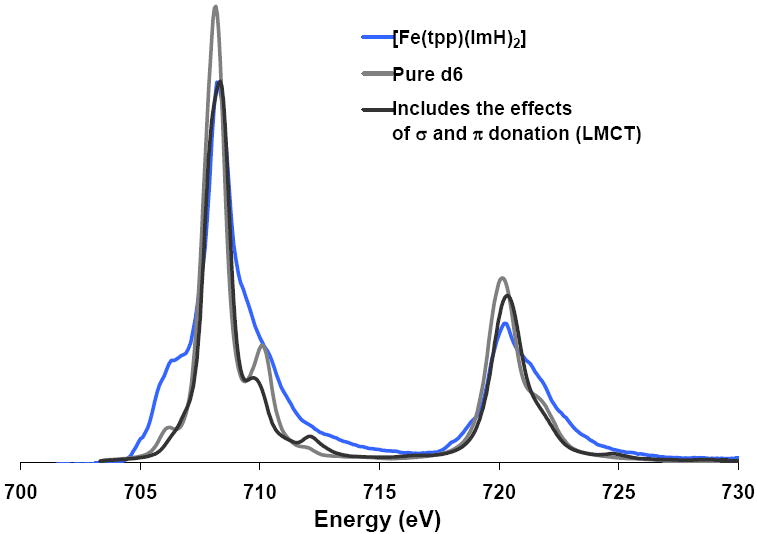
The Fe L-edge spectrum of [Fe(tpp)(ImH)₂] (blue) compared to a calculated pure d⁶ ground state split by the DFT calculated ligand field (light grey) and a simulation which includes the effects of ligand-to-metal charge transfer (dark grey).

2.2. Multiplet simulation: the effect of π back-bonding on spectral shape

From our previous studies, the presence of a low lying ligand π* orbital can have a significant effect on the shape of the Fe L-edge.⁵⁰ This has been attributed to two mechanisms. First, occupied metal character is mixed into the unoccupied ligand π* orbital through back-bonding. Transitions to the metal character in these π* orbitals provide a new mechanism for gaining intensity. Second, a ground state having back-bonding (i.e. MLCT CI) is given by |2p⁶t_2g⁶> + |2p⁶t_2g⁵π^->. This produces L-edge excited states |2p⁵t_2g⁶e_g¹> and |2p⁵t_2g⁵e_g¹π^->,⁹⁸ which can CI mix, and thereby shift intensity from the 2p → e_g transition to the 2p → π* transition packet.⁵⁰

Figure 5 shows a series of simulations (grey) which systematically include the different bonding interactions, (experimental spectrum is given in blue). Spectrum A is a pure Fe(II) low spin ground state, which does not include σ or π donation or π back-bonding. Spectrum B includes only the effects of π back-bonding, and spectrum C includes π back-bonding and σ and π donation. In adding π back-bonding to a pure d⁶ low spin ground state (Figure 5, A to B), the spectrum becomes broader, and more consistent with the experimental spectrum. The VBCI spectral simulations can be interpreted in terms of differential orbital covalency (DOC), by the projection method described previously.⁴⁸ Simulation B gives 9% back-bonding from the Fe d_xz/d_yz orbitals into the porphyrin π* orbitals, but includes no donor bonding. When donor bonding effects are also included (mostly σ, simulation C), the simulation changes slightly but the covalency values obtained are very similar. The final simulation gives 67% metal character in d_x²-y², 65% metal character in d_z², and 11% metal character in the porphyrin π* orbital. If the back-bonding is increased, the simulated spectrum is either too broad or an additional peak appears, which is inconsistent with the experimental spectrum, Figure S4B and C.

Figure 5.

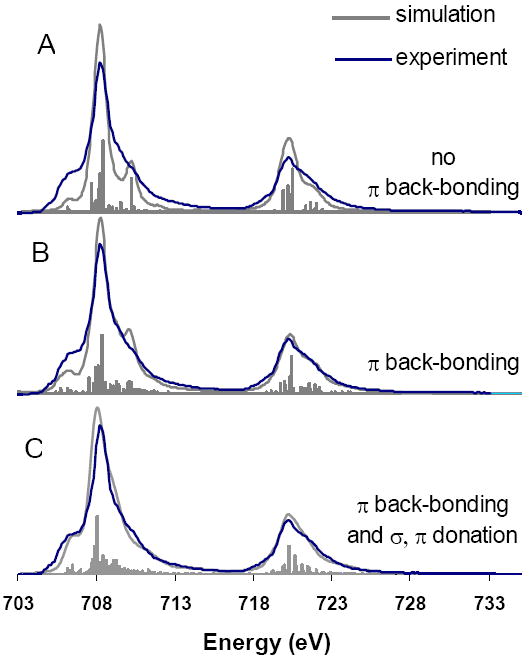
The effect of systematically adding π back-bonding and σ and π-donation to a d⁶ ground state. The grey simulated curves in each case integrate to the same intensity, the lines below each spectra represent the individual transitions contributing to the spectra.

2.3. Comparison to DFT calculations

From the VBCI simulations scaled to total intensity⁹⁹ the amount of metal character mixed into the unoccupied porphyrin 4e_g π* orbitals is around 11% for the Fe(II) complex. This amount of back-bonding is consistent with the DFT calculations which give 9% in the d_xz/yz orbitals. From experiment, the % metal character in the d_x²-y² and d_z² is 65% and 67% respectively; the DFT calculations give 66% for both.

3. VBCI simulations of the Fe(III) L-edge

3.1. Multiplet simulation: the effects of σ- and π-donation

As for Fe(II), the VBCI simulations of the Fe(III) spectrum of [Fe(tpp)(ImH)₂]Cl were performed in D_4h symmetry¹⁰⁰ and required ligand-to-metal charge transfer (LMCT) CI mixing, i.e. a d⁵ + d⁶L ground state. The parameters T_i and Δ were varied to fit the data, starting from the parameters used to fit the non-heme spectrum of [Fe(tacn)₂]Cl₃,⁴⁸ (Table 4) shown in gray for comparison in Figure 6A. To simulate the main spectral change in going to a heme complex, it was necessary to increase the π donor interaction of the heme ligand. The effect of this is shown by the differences in simulations A and B, Figure 6, the decrease in intensity and shift in energy of the lowest energy peak on the L₃ edge. This change alone does not adequately simulate the spectrum of [Fe(tpp)(ImH)₂]Cl since the main feature is still too sharp. The closest fit to experiment (C) is found if the d_x²-y² orbital moves to higher energy and is more covalent than the d_z² orbital. The parameters used in these simulations are given in Table S2 and Table S3.

Table 4.

Parameters for three configuration simulations of K₃[Fe(CN)₆], K₄[Fe(CN)₆]⁵⁰, [Fe(tpp)(ImH)₂] and [Fe(tpp)(ImH)₂]Cl

Compound	ˆ Configuration Separations				MLCT Mixing* Parameters				LMCT Mixing* Parameters				Ligand Field*
	EG2	EF2	EG3	EF3	d5L--d6T(b1)	d5L--d6T(a1)	d5L--d6T(b2)	d5L--d6T(e1)	d6-d7LT(b1)	d6-d7LT(a1)	d6-d7LT(b2)	d6-d7LT(e1)	10Dq	Dt	Ds
K3[Fe(CN)6] 50	1.00	0.50	-1.00	-1.50	0.9	0.9	2.0	2.0	1.9	1.9	0.0	0.0	3.7	0.0	0.0
K4[Fe(CN)6] 50	2.06	1.56	2.00	0.00	0.8	0.8	1.6	1.6	1.7	1.7	0.0	0.0	3.9	0.0	0.0
[Fe(tpp)(ImH)2]Cl	1.40	1.60	0.00	0.00	0.0	0.0	0.7	1.3	4.4	3.2	1.0	2.7	2.2	0.028	0.0
[Fe(tpp)(ImH)2]	1.40	1.60	1.00	-1.00	0.0	0.0	0.0	0.8	2.8	2.8	1.6	2.9	1.63	0.008	0.019

^*These parameters are for the 2p⁶ initial state and 2p⁵ final sate. These ligand field parameters and T and Δ will decrease upon going to the final state and the effects of changing their values in the 2p⁵ final state have been evaluated, see Figure S9. It is found that final state changes do not affect the results of the DOC analysis of the initial state in these highly covalent systems.

^ˆThese parameters are defined relative to the d^N-1 configuration. i.e. EG1=0.

Figure 6.

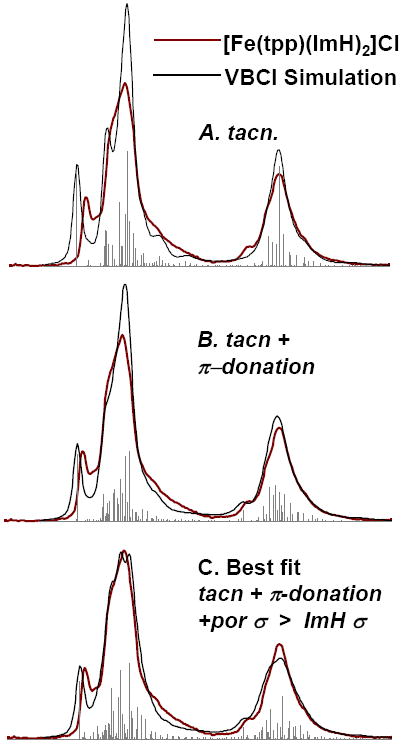
Steps toward the simulation of [Fe(tpp)(ImH)₂]Cl L-edge spectra. In each case the experimental spectrum of [Fe(tpp)(ImH)₂]Cl (red) is superposed on a simulated spectrum (grey). A. The [Fe(tacn)]Cl₃ simulation from ref 33. B. The addition of π donation into d_xz/d_yz to simulation A. C. The best fit of [Fe(tpp)(ImH)₂]Cl, which incorporates both differences in the covalency of d_x2-y2 and d_z2, as well as the effects of π donation into d_xz/d_yz.

To interpret the spectral changes in terms of metal-ligand covalency, the best fit VBCI simulation (Figure 4B) was projected onto the D_4h symmetry components (A_1g, B_1g, E_g and B_2g) as described in reference ⁴⁸. Table 3 gives the values for covalency derived from both the VBCI analysis and from the DFT calculations described above. The VBCI simulation gives the metal characters in the Fe d orbitals as d_x²-y², 52%; d_z², 68%; and d_xz/d_yz, 57%, (Table 3). Note that in D_4h symmetry the d_xz and d_yz orbitals have the same energy and covalency while in the actual complex the lower symmetry associated with axial π donor ligands localizes the hole in the d_yz orbital. This difference is ascertained from the VBCI model by setting the e_g(D_4h) orbital at the same energy as the d_yz “hole” orbital. The largest differences upon going from non-heme to heme Fe are the increased covalencies in both the d_x2-y2 and the d_xz/d_yz orbitals. The d_x2-y2 orbital goes from having 63% metal character in non-heme tacn to 52% metal character in the heme complex, which reflects the increased σ donation from the porphyrin. The d_xz/d_yz goes from having 99% metal character in the non-heme tacn ligand system to 50% metal character in the heme complex, which reflects the substantial π donation from both the porphyrin and the axial imidazole. The metal character in the d_z² orbital largely reflects the σ covalency of the axial imidazoles which is similar in the heme and non-heme cases with around 65% metal character, which indicates that the ImH ligand acts as a σ donor, of comparable strength to tacn, (Table 3).

Table 3.

A comparison of calculated and experimental covalency values for covalency for the compounds: [Fe(tpp)(ImH)₂]⁺, [Fe(tacn)₂]³⁺, [Fe(tpp)(ImH)₂] and [Fe(tacn₂)]²⁺

	Total Intensity	% Total Metal Character in unoccupied orbitals† (based on Intensity)	% Total Metal character in unoccupied orbitals† (based on DFT)	A Comparison of VBCI and DFT values for Differential Orbital Covalency. VBCI(DFT) %
				B1 (x2-y2)	A1 (z2)	B2 (xy)	E1 ** (xz, yz)	π* (xz, yz)
[Fe(tacn)2]Cl3	43.8	351	333	63(64)	63(64)	99 (93)	99(93)
[Fe(tacn)2]Cl2	37.4	295	284	74(72)	74(72)	(93)	(93)
A. [Fe(tpp)(ImH)2] Fe(II) π back-bonding only	39.0	309	314	73(66)	73(66)	(83)	(78)	7(9)
B. [Fe(tpp)(ImH)2] Fe(II) σ,π donation, + π back-bonding	39.0	309	314	65(66)	67(66)	(83)	(78)	11(9)
A. [Fe(tpp)(ImH)2]Cl Fe(III) σ,π donation only	38.3	303	333	54(66)	68(62)	93	58(71)	(2)
B. [Fe(tpp)(ImH)2]Cl Fe(III) σ,π donation, + π back-bonding	38.3	303	333	52(66)	68(62)	93	57(71)	2(2)

^**DFT values for the d_xz and d_yz orbitals were averaged for comparison to the VBCI model in D_4h symmetry. The values for each orbital are given in Table 1.

^†The % metal character summed over unoccupied orbitals reflects the combined effects of covalency and back-bonding. In a system with no back-bonding this number divided by the number of holes gives the average % metal character in each orbital. For example, [Fe(tacn)₂]Cl₃, 351/5 =70%, (63*4+99)/5=70

3.2. Comparison to DFT

The total orbital covalency based on the total L-edge intensity gives 303% metal character summed over all unoccupied metal orbitals. The DFT calculations (Table 3) give 333%, which predicts an overall less covalent system than observed experimentally. The experimental differences in the VBCI analysis (π donation into d_yz and σ donation into d_x²-y² and d_z²) are also reflected in the DFT calculations. The ratio of experimental: DFT calculated metal character for each symmetry set of orbitals is: d_x²-y² 52:62; d_z² 68:64; and (d_yz) 52:71 %. The main difference between experiment and the DFT calculation at the BP86 level is the larger relative contribution of π-donation into d_yz in the data and the larger difference in σ donation to d_x²-y² and d_z².

3.3. Evaluation of possible back-bonding

For completeness a contribution of π back-bonding was added to the simulation of the spectrum of the low spin Fe(III) heme complex. If a small contribution of back-bonding (~2-3%) is added, slightly better agreement with experiment is observed; the spectrum changes shape to higher energy as indicated by the red arrow in Figure S4A. If more back-bonding is added, (>4%) the spectral shape is inconsistent with the experimental spectrum. These observations indicate that back-bonding from Fe(III) into the 4e_g (D_4h) π* orbitals of the porphyrin is very limited, which is consistent with earlier conclusions from NMR spectroscopy.^29,42 When the simulation that includes both π back-bonding and σ and π donation is split into its symmetry components, it gives differential orbital covalencies very similar to those reported above for Fe(III) [Fe(tpp)(ImH)₂]Cl in which the effects of back-bonding were not included, Table 2. This is consistent with the DFT calculations which indicate very limited (2%) back-bonding in the low spin Fe(III) heme complex.

Discussion

The d manifold in heme compounds has been very difficult to study experimentally because the porphyrin based π → π* transitions obscure the metal-based transitions. In this study we have applied Fe L-edge x-ray absorption spectroscopy at the L₃ and L₂ edges to directly probe the Fe d-orbitals of heme complexes and quantify the σ and π donor as well as π acceptor contributions to bonding.

Figure 7 compares the L₃-edge spectrum of an Fe(III) non-heme reference complex, [Fe(tacn)₂]Cl₃, to that of the Fe(III) site in [Fe(tpp)(ImH)₂]Cl. The set of spectra are given twice, to the left the non-heme is colored and the heme is in grey, and to the right the reverse. Superimposed on the spectra are the orbital energies and the % metal character in each orbital calculated from a combination of total intensity and a VBCI analysis of spectral shape, as discussed in the analysis. The line offset from the orbitals compares the weighted average energy of the d-manifold intensity. The feature arising from the 2p⁶t_2g⁵ →2p⁵t_2g⁶ transition (the t_2g feature) is indicated.

Figure 7.

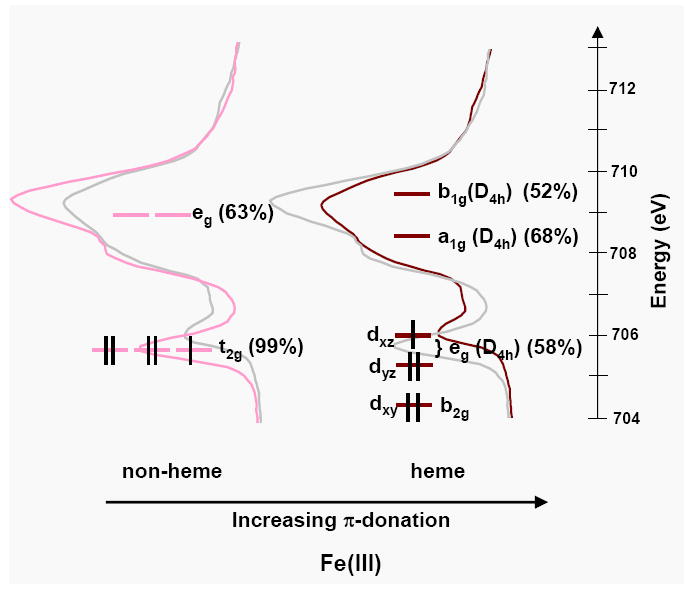
The Fe d-orbital energy levels superimposed on the L₃ spectra of [Fe(tacn)₂]Cl₃ and [Fe(tpp)(ImH)₂]Cl. The % metal character in the d-orbitals calculated from a combination of spectral simulations and total intensity are given in parentheses.

From Figure 7 it is clear that the t_2g feature is both closer in energy to the main multiplet packet and much lower in intensity in a heme relative to non-heme environment. This difference is due to the effect of strong π donation perpendicular to the plane of the porphyrin, which shifts the heme Fe d_xz/d_yz (e_g) orbitals to higher energy and decreases the metal character, thus decreasing the intensity of the t_2g feature.¹⁰¹ These observations have been quantified using the VBCI model, which allows the separation of multiplet and ligand field effects from those of covalency on spectral shape.

In addition to the significant π-donation we also find that the heme ligand set acts as a strong σ-donor relative to amine ligation. This is evident from the Fe(III) L-edge in three ways; the energy shift, the total intensity and the spectral shape. The spectra of both heme and tacn Fe(III) have the same energy shift yet the heme spectrum has lower intensity (Figure 7). The difference in intensity indicates that the effective nuclear charge on the Fe(III) is lower in the heme complex. In the absence of other effects this difference in Z_eff would shift the heme spectrum to lower energy. However, because there is no difference in energy, there must be a ligand field contribution dominated by σ bonding that opposes the energy change of Z_eff. From the VBCI model, the change in shape of the main multiplet packet is a consequence of the d_x²-y² orbital being more covalent than the d_z² orbital, indicating that the heme ligand is a stronger σ-donor than the axial imidazole ligand resulting in a tetragonal anisotropy of the σ bonding.

Figure 8 shows three sets of low spin Fe(II) spectra. Spectrum a) is that of non-heme [Fe(tacn)₂]Cl₂, spectrum b) is that of the heme compound [Fe(tpp)(ImH)₂] and spectrum c) is that of K₄[Fe(CN)₆].⁵⁰ As in Figure 7, the set of three spectra are repeated in grey for reference to one another, and the % metal character in each orbital obtained from experiment is given in brackets.

Figure 8.

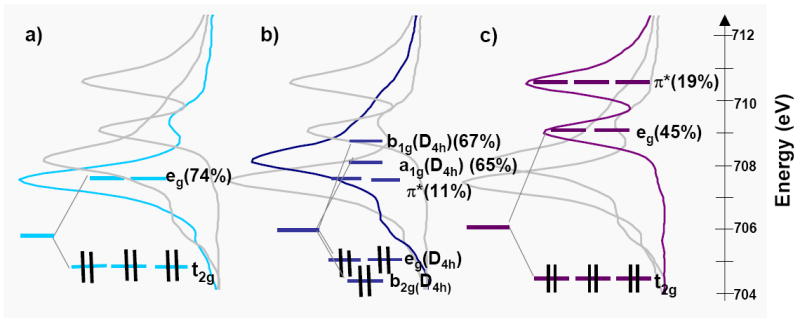
The Fe d-orbital energy levels superposed on the L₃ spectra of a) [Fe(tacn)₂]Cl₂, b) [Fe(tpp)(ImH)₂] and c) K₄[Fe(CN)₆]. The % covalencies calculated from a combination of spectral simulations and total intensity are given in parentheses. In each case all three spectra are given, the grayed spectra are included for reference.

As for the low spin Fe(III) heme complex, the effects of strong σ-donation by the porphyrin are evident in the Fe(II) L-edge spectra from the spectral shift and total intensity. The spectrum of the Fe(II) heme complex shifts 0.7 eV to higher energy relative to the spectrum of the Fe(II) non-heme complex. However, their total intensities and therefore Z_eff are about the same for heme relative to non-heme, which indicates that the larger ligand field due to strong σ donation of the heme shifts the transitions to the d_x²-y² and d_z² orbitals to higher energy, as indicated in Figure 8a e_g (in D_4h) and 8b (a_1g and b_1g, in D_4h).

The addition of back-bonding into the ligand π* orbitals can have a significant effect on both the Fe L-edge spectral shape and total intensity. Since the Fe L-edge results from transitions to the unoccupied Fe d-orbitals, the mixing of occupied metal character into the unoccupied ligand π* orbitals provides an additional intensity pathway. Further, CI mixing between the metal unoccupied e_g(D_4h) and π* orbitals due to back-bonding changes the spectral shape. If we first compare the tacn to the CN^- spectra (spectrum a to c), a significant difference is observed as the spectrum of K₄[Fe(CN)₆] has a second main feature that has been assigned as arising from a transition to the ligand π* orbital. This transition borrows intensity from the main transition to the e_g set of d orbitals to make the contribution of the ligand π* very pronounced.⁵⁰ In going from [Fe(tacn)₂]Cl₂ to [Fe(tpp)(ImH)₂] (spectra a and b) the spectrum becomes broader, but does not show the pronounced π* peak of the CN^-. This broadening is a consequence of the addition of a small amount of π* intensity in an orbital located close in energy to the main e_g orbital set.⁵⁰ Thus there is back-bonding in the Fe^II heme complex but it is much less than in ferrocyanide (11(2)% vs 19(3)%).⁵⁰

The rather limited metal character in the π* orbital reflects the fact that the heme ligand does not act as a particularly good π acceptor, yet the porphyrin π* orbital is closer in energy to the d orbitals than the CN^- π* orbitals in ferrocyanide. This reflects the fact that the heme system 4e_g(D_4h) π* orbital contains small nitrogen orbital coefficients so that it does not substantially overlap with the metal. For comparison, DFT calculations show the CN^- π* acceptor orbitals have about 60% total carbon character whereas the heme π* acceptor orbitals have only 30% total nitrogen character. In the Fe(III) heme system when more than 2% back-bonding was included in the VBCI simulation the spectrum either became too broad or an additional peak appeared, which indicates that the back-bonding from Fe(III) to heme is not significant. Upon going from Fe(II) to Fe(III), the d-orbitals contract and decrease in energy, due to the increase in Z_eff and thus lead to the very low back-bonding observed both experimentally and from DFT calculations.

Understanding the degree and origin of the π delocalization of heme systems has important implications for understanding the reactivity of heme centers in biology. The fast electron-transfer rates in proteins are facilitated by super-exchange coupling through either hole or electron super-exchange pathways which enhance the interactions between donor and acceptor redox sites.^103-105 For a super-exchange mechanism to be efficient, the redox-active MO must have sufficient delocalization through the protein. In the cytochromes, a hole super-exchange mechanism would be facilitated by a strong π donor interaction of the heme 3e_g orbital with the d_yz hole of the oxidized Fe(III) site. An electron super-exchange mechanism requires substantial mixing of the reduced Fe(II) valence d orbitals with the heme 4e_g orbital through π back-bonding. In this study we have experimentally quantified the π donation to Fe(III) and the π back-bonding from Fe(II). π donation to low-spin Fe(III) produces a redox-active molecular orbital that is 50% metal and 50% ligand, whereas π back-bonding from Fe(II) produces an HOMO which has 90% metal and 10% ligand character. The coefficients of mixing indicate that a hole super-exchange mechanism likely dominates.

Thus the interaction of the d_π redox active ferric molecular orbital (RAMO) with the 3e_g π heme donor orbitals determines the hole super-exchange pathway. In the limit when no axial ligands are attached to the Fe in the porphyrin, the d_xz and d_yz based orbitals are degenerate and equally mix with the porphyrin 3e_g orbitals. In a “real” system, this degeneracy will be lifted through axial π bonding interactions or through distortions either in the plane or from the plane of the porphyrin. If two eclipsed ImH ligands are bound to heme, the ImH π donor orbitals (perpendicular to the ImH plane) interact with only one d_π-orbital, and this will localize the RAMO d_π hole. Figure 9(a) shows the two degenerate porphyrin π donor 3e_g(D_4h) orbitals, labeled A and B. When the imidazoles are oriented with their molecular planes in the xz plane (i.e. the plane along N-Fe-N axis), as in Figure 9(b) the LUMO localizes into the Fe3d_yz + 3e_g(A-B) combination, creating a highly directional MO for super-exchange. If the ImH ligands are eclipsed but rotated such that their planes are no longer along the N-Fe-N axis these coefficients change.¹⁰⁶ When they bisect the N-Fe-N porphyrin angle (Figure 9(c)), the 3e_g(D_4h) mixed into the LUMO is delocalized over the porphyrin. Finally, if the ImH ligands are staggered (perpendicular to each other), each ImH ligand π donates into a different d_π orbital and the effective orbital symmetry is D_4h. In such a case the system will be unstable to a symmetry-breaking distortion of the heme plane. These effects of axial ligand orientation have been discussed elsewhere, in terms of NMR experiments,^{29,30,41,42,106} crystallography¹⁰⁷ and DFT calculations.^108-113

Figure 9.

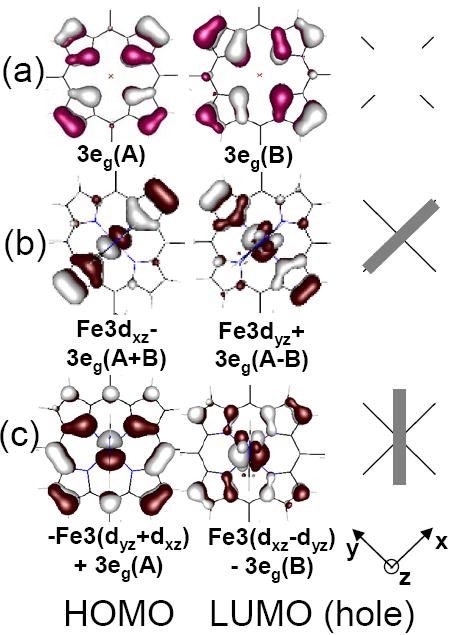
Porphyrin delocalization as a function of axial ligand orientation. (a) The two degenerate porphyrin (3e_g) orbitals, labeled A and B. The delocalization of the HOMO and LUMO orbitals and their coefficients (b) when the ImH ligands are eclipsed and oriented along the y axis, and, (c) when the ImH ligands are eclipsed and bisect the x-axis and y axis. The ImH π orbitals can be seen above and below the porphyrin plane in the LUMO. To the right, the grey rectangles intersecting the black cross indicate the orientation of the axial imidazoles relative to the porphyrin ring.

Extension of these axial ligand effects on the LUMO to heme sites in proteins provides some insights into super-exchange contributions to electron transfer. While there are many different axial ligand orientations observed in the cytochromes two interesting cases are considered in Figure 10. Figure 10a shows the LUMO calculated with ImH oriented as in the cytochrome b₅ family.^117-119 This orbital shows substantial delocalization along the heme edge. Figure 10b shows the LUMO calculated from bovine heart (BH) cytochrome c (1B4Z), which has an axial methionine oriented between the N-Fe-N bond and the plane formed by the C-S-C atoms of the methionine is tilted approximately 45° to the heme normal. In this orientation, the methionine can provide both σ− and π− down interactions with the Fe through its a₁ and b₁ orbitals respectively.¹²⁰ In a single point calculation (i.e. a calculation using the crystal structure coordinates of BH cytochrome c active site, from Figure 10(b) the LUMO has a different pattern of delocalization relative to cytochrome b₅, with higher coefficients on one set of β pyrrole carbons. The differences in delocalization between the LUMO in cytochromes b₅ and BH cytochrome c are consistent with the differences in the orientation of the heme groups relative to the surface of the proteins. In cytochromes b₅ the beta and meso positions along one edge (the edge containing the two propionates) are equally exposed, whereas in BH cytochrome c one of the sets of β-pyrrole carbons are most exposed (including one of the covalent thioether attachments to the protein). These differences are indicated by the dotted blue lines, in Figure 10. Thus for both cytochromes b₅ and bovine heart cytochrome c the hole super-exchange pathways are directed to the most exposed part of the heme edge, consistent with experiments which indicate that electron transfer occurs at the exposed heme edge.^119,121

Figure 10.

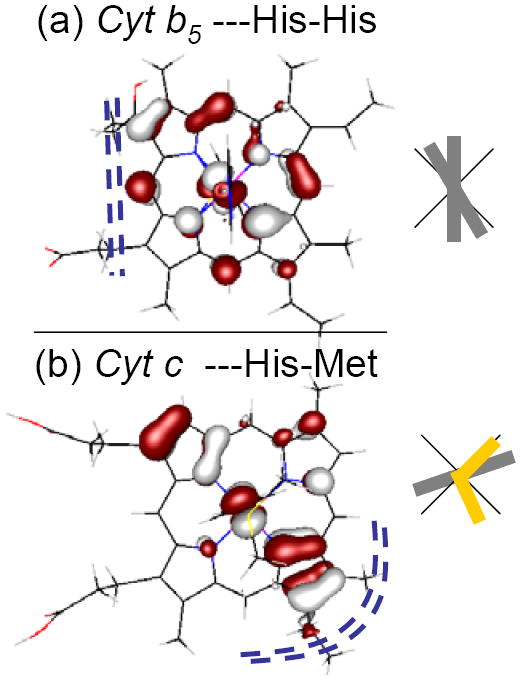
The LUMO orbitals (hole) calculated for the active site of (a) the bis-histidine-ligated heme bovine microsomal cytochrome b₅, 1CYO¹¹⁴ and (b) the histidine-methionine-ligated bovine heart cytochrome c 1B4Z.¹¹⁵,¹¹⁶ The grey rectangles relative to the black cross indicate the orientation of the ImH ligands to the heme, projected into the xy heme plane. The methionine sulfur is at the intersection of the two short yellow rectangles in (b). Dotted blue lines (----) indicate the most exposed part of the heme edge of these two structures.

In a recent study the relative reactivity of an Fe^IV=O heme was compared to an Fe^IV=O non-heme complex.¹²² While the Fe-O bonding of the heme and non-heme systems were found to be similar, the calculations showed that the reaction energy for H-atom abstraction favored the heme system by ~10 kcal per mole. This was attributed to electron delocalization in the Fe^III-OH product in the heme environment. From our studies here, the low spin ferric heme has extensive electron delocalization due to heme π-donation. This could contribute in reactions where Compound II (i.e. Fe^IV=O) may be catalytically relevant.

Summary

In this study we have been able to experimentally quantify the effects of π-donation and π back-bonding for a highly covalent Fe center in a porphyrin environment. We find that the heme ligand acts as a very strong π-donor to Fe(III) and a weak π-acceptor from Fe(II). The relative strengths of the π-donation vs. π-acceptor interactions indicate that electron transfer in the cytochromes likely involves a hole type super-exchange mechanism, that is facilitated by the very strong π donation from porphyrin to Fe(III). This strong heme π donation can also play an important role in stabilizing Fe(III) in catalytic cycles.