Mechanical Buckling of Veins under Internal Pressure

Abstract

Venous tortuosity is associated with multiple disease states and is often thought to be a consequence of venous hypertension and chronic venous disease. However, the underlying mechanisms of vein tortuosity are unclear. We hypothesized that increased pressure causes vein buckling that leads to a tortuous appearance. The specific aim of this study was to determine the critical buckling pressure of veins. We determined the buckling pressure of porcine jugular veins and measured the mechanical properties of these veins. Our results showed that veins buckle when the transmural pressure exceeds a critical pressure that is strongly related to the axial stretch ratio in the veins. The critical pressures of the eight veins tested were 14.2 ± 5.4 mmHg and 26.4 ± 9.0 mmHg at axial stretch ratio 1.5 and 1.7, respectively. In conclusion, veins buckle into a tortuous shape at high lumen pressures or reduced axial stretch ratios. Our results are useful in understanding the development of venous tortuosity associated with varicose veins, venous valvular insufficiency, diabetic retinopathy and vein grafts.

INTRODUCTION

Tortuous veins are often seen in patients in many different disease processes. Tortuous varicose veins cause morbidity and are a common manifestation of chronic venous disease. ³ Varicose veins are often associated with venous hypertension and valvular insufficiency ^{3, 34, 40} and have a very high prevalence in over one third of the aged populations.^{7, 26} Tortuous conjunctival and retinal arteries and veins are also often observed in patients with diabetic retinopathy and hypertension. ^{8–10, 21, 32} In addition, tortuous venules also have been observed in cerebral, coronary, digital, and other vascular beds. ^{22, 30} Furthermore, veins are commonly used in dialysis access procedures ^{1, 13} and as grafts to bypass diseased arteries; ^{33, 44} veins graft may become tortuous under the arterial pressures if not sufficiently stretched axially. ^{16, 39}

Though tortuous veins are widely observed, the underlying mechanisms are poorly understood. Venous tortuosity may affect blood flow and venous wall remodeling and therefore be associated with venous diseases. It has been reported that tortuous veins lead to sluggish blood flow and thrombosis. ^{11, 29} Therefore, it is of paramount clinical interest to understand the mechanisms of venous tortuosity.

We have recently shown that straight arteries may become tortuous due to mechanical buckling under internal pressure.^{18, 20} It is plausible that veins also buckle under internal pressure and thus, become tortuous. Therefore, the objectives of this study were to determine the critical loads that induce vein buckling and to determine the biomechanical mechanism by which veins become tortuous.

MATERIALS AND METHODS

Vein procurement and preparation

Internal and external jugular veins were harvested from 6 to 7 month-old farm pigs (100–150 kg) at a local abattoir by midline incision. The veins were rinsed with Dulbecco’s phosphate buffered saline (PBS, Sigma Chemical, St. Louis, MO), placed in ice-cold PBS, and transported to our laboratory. After excess connective tissue was removed, the veins were rinsed with PBS and tied to two luer connectors (Cole-Parmer, Vernon Hill, IL) at both ends; one end was connected to a 10 mL syringe while the other end was occluded. The veins were inflated with air while submerged in PBS to detect leaks. Vein segments without leaks or side branches were selected and the in vitro free lengths were measured with calipers.

Inflation test

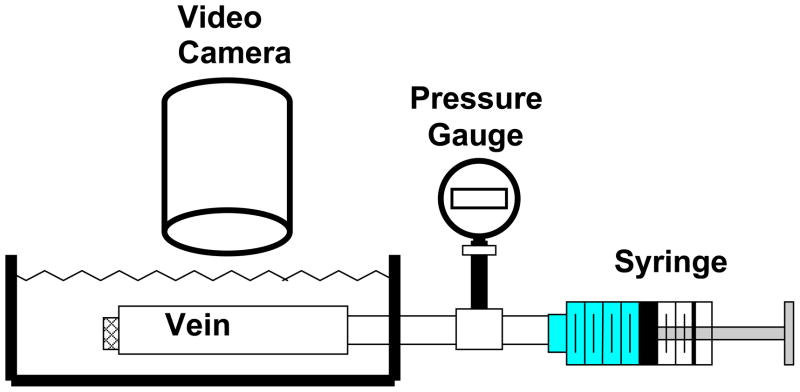
To obtain the stress strain relationship for the porcine veins, a pressure-inflation test was used to determine the vein deformation under internal pressure. Briefly, veins were inflated with PBS while one end was free to move longitudinally; this allowed the veins to expand freely in both the radial and axial directions (Figure 1). While veins are normally under a pressure of less than 10 mmHg ^{2, 23}, we tested the veins beyond this limit to determine the potential reserves in terms of buckling. Thus, veins were preconditioned by gradual inflation with PBS to a pressure of approximately 50 mmHg and deflating to 0 mmHg for several cycles until the veins reached a reproducible deformation. After preconditioning, the veins were inflated multiple times for data acquisition. The outer diameter and axial length of the veins were recorded simultaneously with a digital camera (Sony, San Diego, CA) as the lumen pressure was increased. The lumen volume was measured using a micropipette during the inflation process. Vessel lengths and diameters were measured from the digital photos using Image-Pro Plus^® (Media Cybernetics, Silver Spring, MD). All length and diameter measurements were repeated three to five times and averaged to represent the value. The errors of length and diameter measurements were estimated to be less than 0.2 mm and 0.03 mm, respectively.

Figure 1.

Schematic illustrating the experimental set ups for vein inflation tests. Vein segments mounted in the tissue chamber were inflated with PBS using a syringe pump while the deformation was captured by the camera.

Measurement of critical buckling pressure and deflection

To determine the critical pressure, veins were secured at both ends to cannulae inside a tissue chamber designed in our lab as part of an artery organ culture system, as previously described.¹⁷ The cannulae were connected to a pressure meter and a syringe pump. The veins were stretched axially to achieve designated axial stretch ratios (1.1, 1.3, 1.5, and 1.7) and gradually pressurized with PBS using the syringe pump. The veins were photographed at pressure increments of 1, 2, or 5 mmHg until a large deflection (about 3 to 8 mm depending on the vessel length) was reached. Different incremental values were used based on the range of the critical buckling pressure to acquire a similar number of incremental steps for each vein. A preliminary reading of the critical pressure was recorded when veins began to exhibit visually detectable deflection. This process was repeated three times for each vein and the process was also recorded with the digital camera.

Later, the deflections of the veins under pressure were measured from the video and photos taken during the buckling test using ImagePro Plus^®. First, the positions of the central lines of the veins at all pressure levels were determined by averaging the coordinates of the two edges of the veins. Then, the displacement of the central line at the maximum deflection point (in the middle of the vessel length) from its baseline position at zero pressure was determined and defined as the deflection of the vein. The critical pressure was determined as the pressure when the vein deflection became detectable (~0.5 mm) from the initial baseline.

Measurement of initial dimensions

After the buckling tests, veins were cut into short rings and photographed for measurement of the initial diameter (circumferential length) and wall thickness. The rings were then fixed in 10% formalin for histology.

The stress-strain relationship

Since the vein walls were very thin, a thin-walled tube model was used for the stress and strain analysis. The outer diameter, inner (lumen) diameter, wall thickness, and axial length of the veins were denoted by D_o, d_o, t_o, L_o and D, d, t, L at initial un-deformed condition and under internal pressure p, respectively. The circumferential stretch ratio λ_θ was determined as the change of the middle wall diameter while the axial stretch ratio λ_Z was determined as the change in the axial length of the veins:

$${\lambda }_{\theta }=\frac{D+d}{D_o+d_o},{\lambda }_Z=\frac{L}{L_o},$$ (1)

The circumferential stress was calculated using Laplace’s law and the axial stress σ_Z was calculated by multiplying the pressure by the lumen cross-sectional area divided by the wall cross-sectional area.

$${\sigma }_{\theta }=\frac{p(d+D)}{4t},{\sigma }_z=\frac{{pd}^2}{D^2-d^2}$$ (2)

While the initial dimensions (D_o, d_o, t_o, L_o) were directly measured, the outer diameter D and vessel length L under pressure were measured from the recorded deformation images, the lumen diameters d of the deformed veins were determined based on the wall incompressibility conditions that gives:

$$d=\sqrt{D^2-\frac{L_o}{L}(D_o^2-d_o^2)}\text{and}t=\frac{D-d}{2}$$ (3)

The veins demonstrated a nonlinear stress-strain relationship. The experimental axial stress versus stretch ratio data were fitted with an exponential function proposed by Fung ¹⁴

$${\sigma }_z=\beta (e^{\alpha ({\lambda }_z-1)}-1)$$ (4)

where α and β are material constants. Accordingly, the incremental modulus is given by¹⁴

$$E_{\mathit{inc}}=\frac{d\sigma }{d\lambda }=\alpha ({\sigma }_z+\beta )$$ (5)

In addition, we defined an “average” modulus, E_avg, as

$$E_{\mathit{avg}}=\frac{{\sigma }_z}{{\lambda }_z-1}$$ (6)

Theoretical estimation of critical pressure

For thin-walled blood vessels with a linear elastic material under internal pressure, Han previously developed a buckling equation to predict the critical buckling pressure ¹⁸:

$$p_{cr}=E[{\pi }^2{(\frac{a}{L/2})}^2+2({\lambda }_z-1)](\frac{t}{a})$$ (7)

Where p_cr is the critical buckling pressure, E is the Young’s modulus, L is the vessel length, a is the lumen radius of the vessel, t the wall thickness of the vessel, and λ_Z is the axial stretch ratio.

This equation was based on the assumption that σ_Z = E(λ_Z − 1) for linear elastic materials and by re-writing E(λ_Z − 1) in this equation back to σ_Z, we have ^{18, 20}

$$p_{cr}=[E{\pi }^2{(\frac{a}{L/2})}^2+2{\sigma }_z](\frac{t}{a})$$ (8)

To test whether these equation are applicable to veins, we estimated the critical pressure of the veins using equation (7) with the average modulus E_avg and then using equation (8) with the axial stress σ_Z and incremental modulus E_inc given in equations (4) and (5). These estimated critical pressures were compared to the experimental measurements.

RESULTS

A total of eight veins (5 internal jugular veins and 3 external jugular veins) were tested. The lengths of the vein segments ranged from 26.2 to 42.0 mm with an average diameter of 6.5 mm (Table 1).

Table 1.

Summary of the initial dimensions of the veins tested.

Vein	Length (mm)	Diameter (mm)	Wall Thickness (mm)
1	42.0	7.75	0.30
2	37.2	7.55	0.32
3	27.3	5.26	0.31
4	29.7	5.98	0.16
5	30.6	7.70	0.30
6	26.2	4.13	0.24
7	29.9	6.88	0.30
8	23.6	6.87	0.42

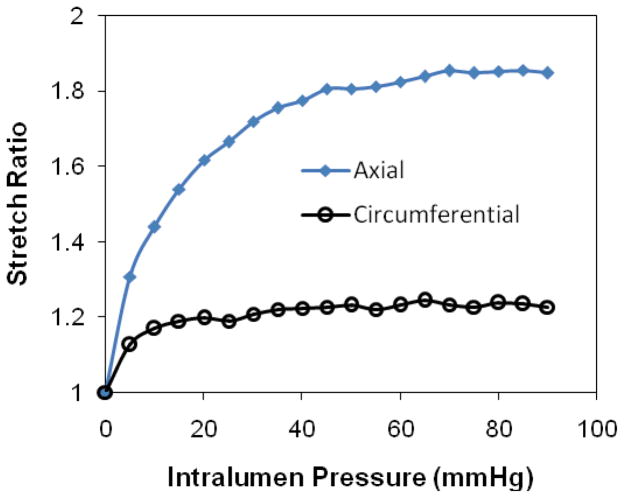
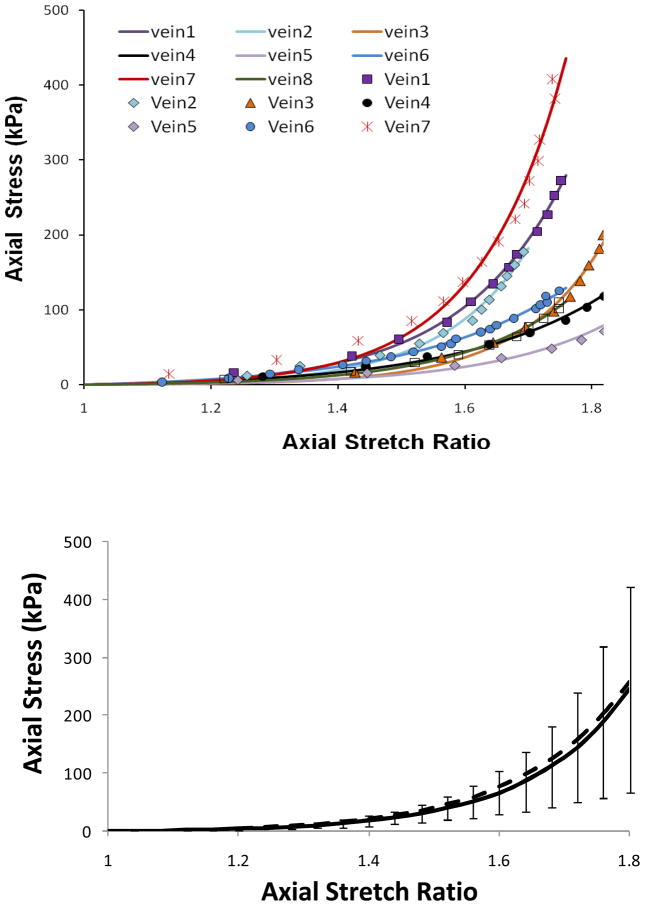
Free vein segments (with one end closed but free to move) enlarged and elongated under intra-lumen pressure (Figure 2). While the length (thus the axial stretch ratio) increased consistently with increasing pressure, the diameter (thus the circumferential stretch ratio) first increased but then become nearly flat when the pressure exceeds ~20 mmHg. The increases in axial stretch ratio from the baseline level were more than two times bigger than the increases in circumferential stretch ratio at all pressure levels, indicating that the wall was stiffer in the circumferential direction than in the axial direction (Figure 2, bottom). The axial stress versus axial stretch ratio curves were nonlinear for all veins (Figure 3). Individual variations in the stress-stretch curves were seen among the veins but no distinct difference was seen between the internal and external jugular veins. The exponential equation (4) fitted the experimental data very well with R² values of 0.984 to 0.997 for all eight veins. The material constants obtained from the fittings are summarized in Table 2. The corresponding mean stress versus stretch ratio curve is shown in Figure 3 bottom panel.

Figure 2.

Deformation of an internal jugular vein expands freely under internal pressure. Top: pressure = 4 mmHg, Middle: pressure =50 mmHg. Bottom: the axial and circumferential stretch ratios plotted as functions of lumen pressure.

Figure 3.

Axial stress plotted with the axial stretch ratio for eight veins underwent pressurized inflation test. The top panel illustrated comparisons of the experimental data (symbols) and the fitting curves in form of equation (4). The bottom panel illustrated the mean value of the eight veins with the error bars represent the standard deviation. The dotted line is the curve generated using the mean values of material constants α and β (see Table 2).

Table 2.

Summary of the material constants α and β of the veins tested.

Vein	α	β (kPa)	R2
1	6.08	2.78	0.997
2	7.24	1.16	0.989
3	7.53	0.40	0.990
4	4.35	3.50	0.995
5	5.34	1.02	0.980
6	4.22	5.48	0.997
7	7.34	1.65	0.984
8	5.80	1.37	0.991
mean	6.08	2.33	0.990
SD	1.29	1.60	0.006

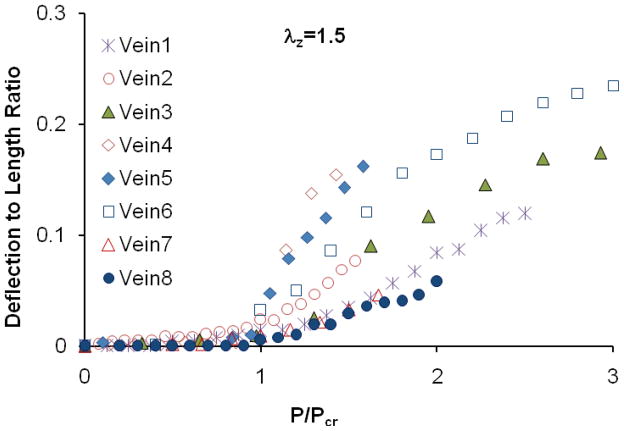
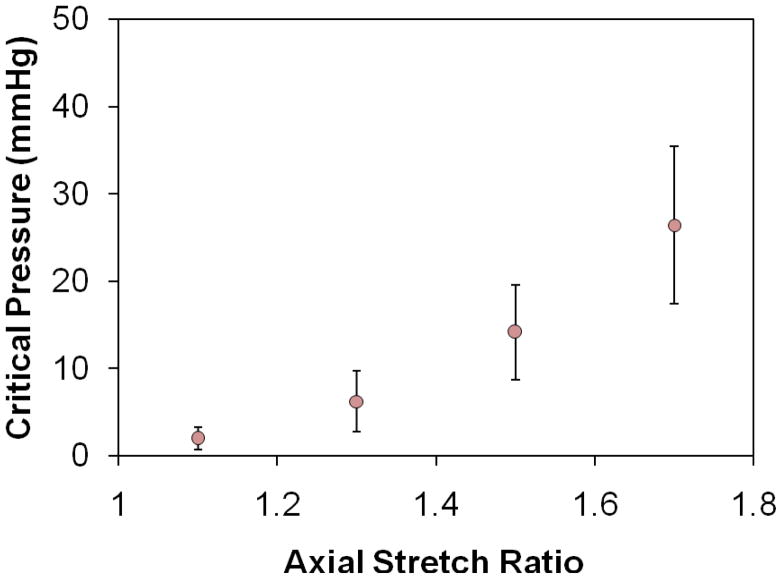
All vein segments tested buckled when the lumen pressure exceeded critical values (Figure 4). When pressurized at a given axial stretch ratio, veins first dilated with diameters increased when the pressure gradually increased from zero, but they did not deflect laterally (Fig. 4, middle). When the lumen pressure exceeded the critical pressure level, veins became buckled (Figure 4 bottom). The deflection started at the critical pressure, increased quickly at the beginning of the buckling process, and was gradually slow down with increasing internal pressure (Figure 5). The critical pressures were obtained at several levels of axial stretch ratios (1.1, 1.3, 1.5, and 1.7) and the results were summarized in Figure 6. It is seen that the critical pressure increased with increasing axial stretch ratio. Variations of critical pressures at given stretch ratios were most likely due to the variations in vein segment length, diameter, wall thickness, and wall stiffness.¹⁸

Figure 4.

A jugular vein under internal pressure. Top: internal pressure =2 mmHg; Middle: internal pressure = 8 mmHg; and bottom: internal pressure =20 mmHg. The axial stretched ratio was 1.5 and the critical pressure was 14 mmHg. Note that this is the same vein as shown in Figure 2.

Figure 5.

Deflection to length ratio of eight veins plotted as functions of internal pressure normalized by the critical pressure.

Figure 6.

Critical buckling pressure of eight veins (mean ± SD) plotted as a function of the axial stretch ratio. The critical pressure increases with increasing axial stretch ratio.

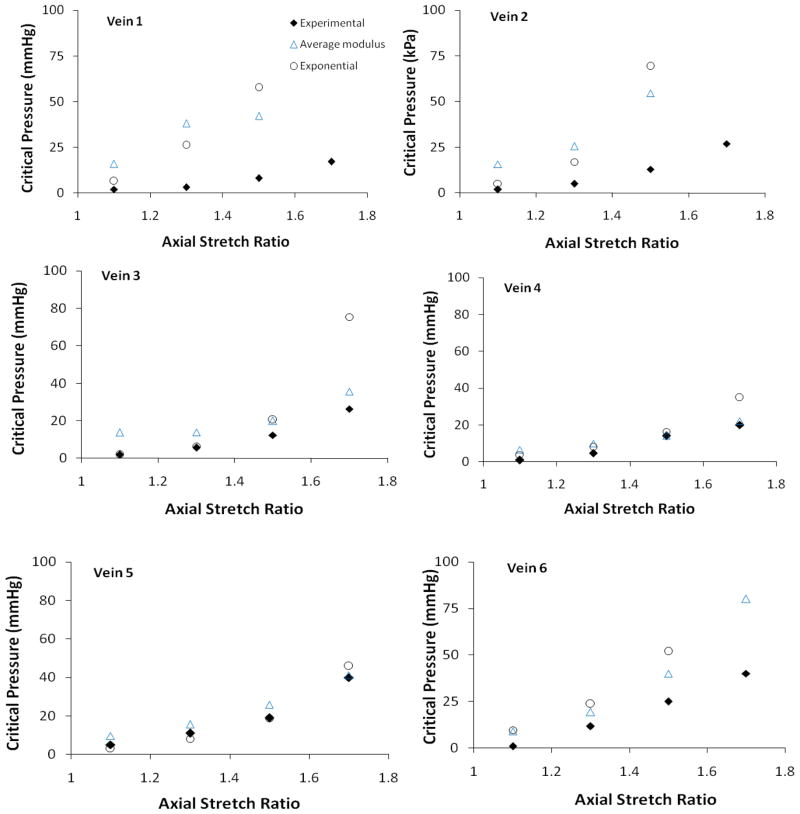
Compared to the experimental measurements, the critical pressures determined from model equations 7 and 8 overestimated the critical pressure (Figure 7). Our results also showed that using the average modulus E_avg with equation 7 produced better estimations of the experimental measurements than using the incremental modulus E_inc with equation 8.

Figure 7.

Comparisons of critical buckling pressures of six veins measured experimentally (solid diamonds) and predicted from the buckling equations (hollow symbols). The hollow triangles represent model predictions using the average modulus. The hollow circles represent model predictions using the exponential stress strain curve and the corresponding incremental modulus. See text for details.

DISCUSSION and CONCLUSIONS

Normal veins experience much lower lumen pressures than arteries and vein lumens collapse under increased external pressure or compression generated by the surrounding tissues. While the lumen collapse of veins has been studied extensively ^{15, 35}, the bent buckling of long vein segments has been largely ignored. A new finding of this study is that long veins may buckle under internal pressure and become tortuous. Our results demonstrated that the critical buckling pressure of veins depended on the axial stretch ratio. The critical pressures of the eight veins tested were 14.2 ± 5.4 mmHg and 26.4 ± 9.0 mmHg (i.e. 1.9 ± 0.7 kPa and 3.5 ± 1.2 kPa respectively) at axial stretch ratios 1.5 and 1.7, respectively. The buckling equation proposed by Han ¹⁸ can be used to estimate the critical pressure of veins.

Veins were tested in PBS solution in this study for its simplicity since our main goal was to demonstrate that vein can buckle under internal pressure. Though veins buckle into a single wave in PBS, veins would buckle into higher order mode shapes of multiple waves with the surrounding tissue support,²⁰ similar to the tortuous veins in vivo. The buckling behavior studied here is an acute effect (deflection) of veins under internal pressure. The long-term effect, i.e. the adaptation of veins under these load conditions needs further investigation.

The elastic modulus determined from the longitudinal stress- stretch ratio curve was used in estimation of critical pressure since our previous model demonstrated that the critical pressure is directly linked to the longitudinal stress and modulus.^{19, 20} The longitudinal modulus is different from the circumferential modulus determined from the diameter changes due to material anisotropy of the veins. Comparison of circumferential and longitudinal modulus can be found in the literature (see e.g. Tanaka and Fung ⁴¹). The model used here provided a simple estimation and future work is needed in applying the 3-D material models to determine the critical pressure^{19, 20}.

Compared to arteries, veins demonstrated similar trends in buckling behavior but the critical pressures of porcine jugular veins were much lower than that of carotid arteries. For example, while a 30 mm jugular vein segment under an axial stretch ratio of 1.5 buckles at a lumen pressure of ~15 mmHg (2 kPa), a carotid artery of 50 mm buckles at a lumen pressure of ~150 mmHg (20 kPa).¹⁸ Another difference is that the model equations over-estimated the critical pressures for the veins compared to the experimental measurements, while they generated very good predictions for the critical pressure of arteries.¹⁸ The experimental measured critical buckling pressures of the jugular veins were much lower than the model predicted values. A possible explanation is that thin-walled veins are more sensitive to geometric and material “imperfections” than the thick-walled arteries. Model equations were developed for ideal cylindrical vessels.^{18, 20} “Imperfections” in the vessels such as geometric and material nonuniformities or defects reduce the critical load.^{15, 42} A small local variation in wall thickness (such as connective tissue attachment to the adventitia) that may be negligible to thick-walled arteries could be a significant “imperfection” to the thin-walled veins and thus reduce the critical pressure of the vein significantly from that of a perfect cylindrical tube.

Clinical studies have shown that tortuous veins are often associated with venous hypertension, vascular wall degradation, and valvular incompetence.^{3, 6, 25, 27, 34} Valvular incompetence leads to venous hypertension. ^{3, 37, 40} Development of tortuous retinal veins and varicose veins has been linked to venous disease and genetic deficiency. ^{24, 28, 31, 38} However, the relationships between venous pressure, vascular wall degradation, and vein tortuosity were poorly understood. Our current results indicated that mechanical buckling could be a possible initiation mechanism for the development of tortuous veins. Since increased venous pressure, reduced axial tension, or weakened vessel wall could cause veins to buckle ¹⁸, venous hypertension, aging, and degenerative vascular diseases all make veins vulnerable to buckle and thus are risk factors for tortuous veins. The significant axial stretch in normal veins maintains the stability of veins against buckling.¹⁶ On the contra, insufficient axial tension, either due to aging, vascular surgery, or excessive vessel growth such as in the case of collateral arteries, could lead to vein buckling and tortuosity.

In addition, tortuous vein grafts have been reported in the clinical setting and animal models.^{4, 5, 12, 39} Our results indicate that either increased internal pressure (arterial pressure) or insufficient axial tension could lead to vein buckling and create tortuosity. While implanting vein grafts of excessive length may lead to low axial tension and tortuous vein grafts, gradual diminishing of axial tension post-surgery ^{16, 39} may also lead to the gradual development of tortuous vein grafts. On the other hand, arterialization and wall stiffening may reduce tortuosity.³⁹ Thus, increasing the axial tension by shortening the length of the vein grafts is therefore an effective approach to avoid tortuous vein grafts.

Venous remodeling is an important component of many disease processes ^{25, 34, 36, 37, 43} and veins exposed to arterial pressures, such as vein grafts used to bypass occluded arteries and dialysis access fistulas, undergo extensive remodeling.^{1, 33, 44} The wall remodeling alters the dimension and mechanical properties of the veins and thus affects their buckling stability. On the other hand, buckling changes the shape and thus affects the wall stress and lumen blood flow in veins. Therefore, the effects of vein buckling on vein wall remodeling need to be further studied to understand the long-term adaptation of the buckled vein.

In conclusion, veins buckle due to an increase in internal pressure or a decrease in the axial stretch ratio or both; buckled veins exhibit tortuous shapes. Mechanical buckling initiated deformation could be a mechanism that leads to the venous tortuosity observed in multiple clinical scenarios.