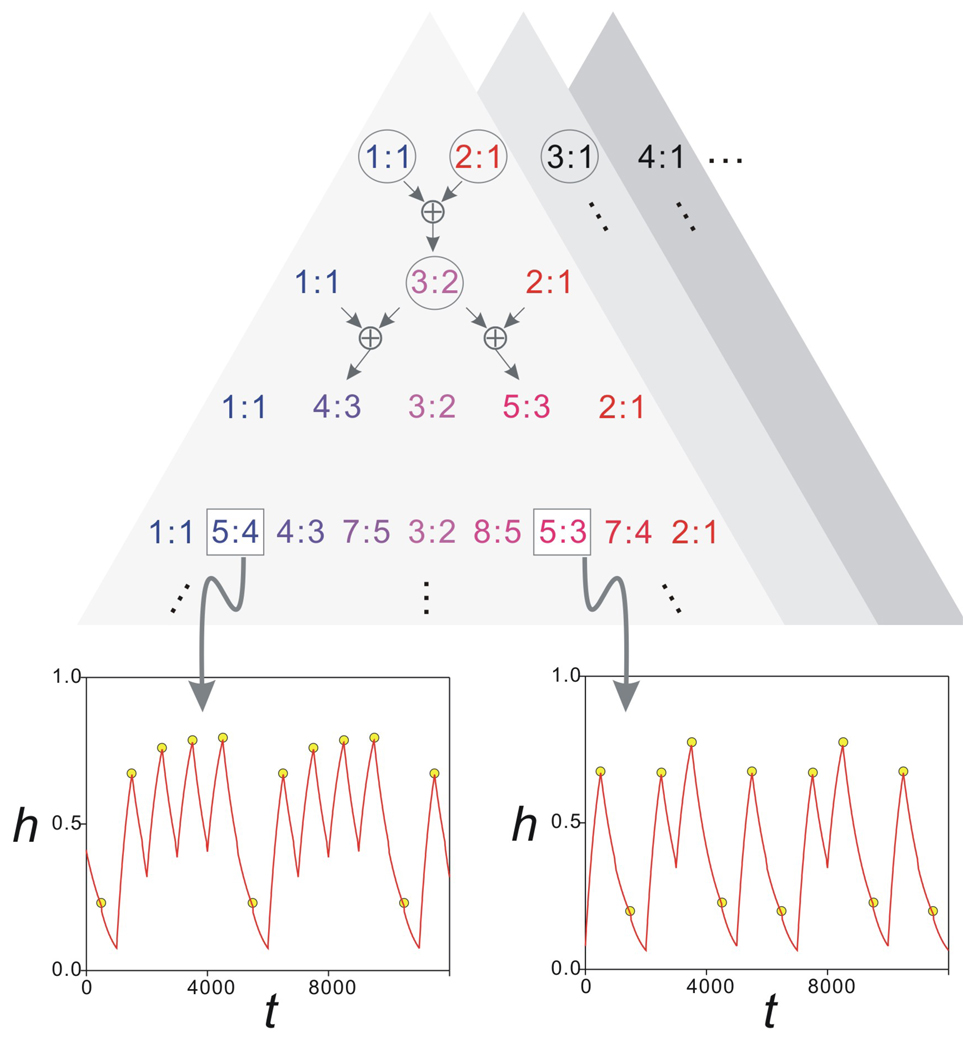
Figure 10.

The generalized Pascal triangle shows the proposed bifurcation structure of the map Π for the parameter g_A. The top level shows the stable solutions that cover the largest intervals of g_A values. These are the intervals marked as 1–4 in Fig. 7. For all n, the g_A interval between the n:1 and n+1:1 solution intervals gives rise to a distinct generalized Pascal triangle (shaded triangles). Each level of the triangle is obtained by adding the adjacent n:m values on the level above using the ⊕ addition operator (top arrows; see text). Only the triangle corresponding to the region between the 1:1 and 2:1 intervals is shown in some detail. The circled n:m values correspond to the solutions shown in Fig. 8. The two insets show two period-five stable solutions of the map Π (yellow circles) superimposed on the time trace of h from Equations (1) (red traces) for the same values of g_A indicating the 5:4 (g_A=4.63 nS) and 5:3 (g_A=5.506 nS) solutions. Other parameters are as in Fig. 8.