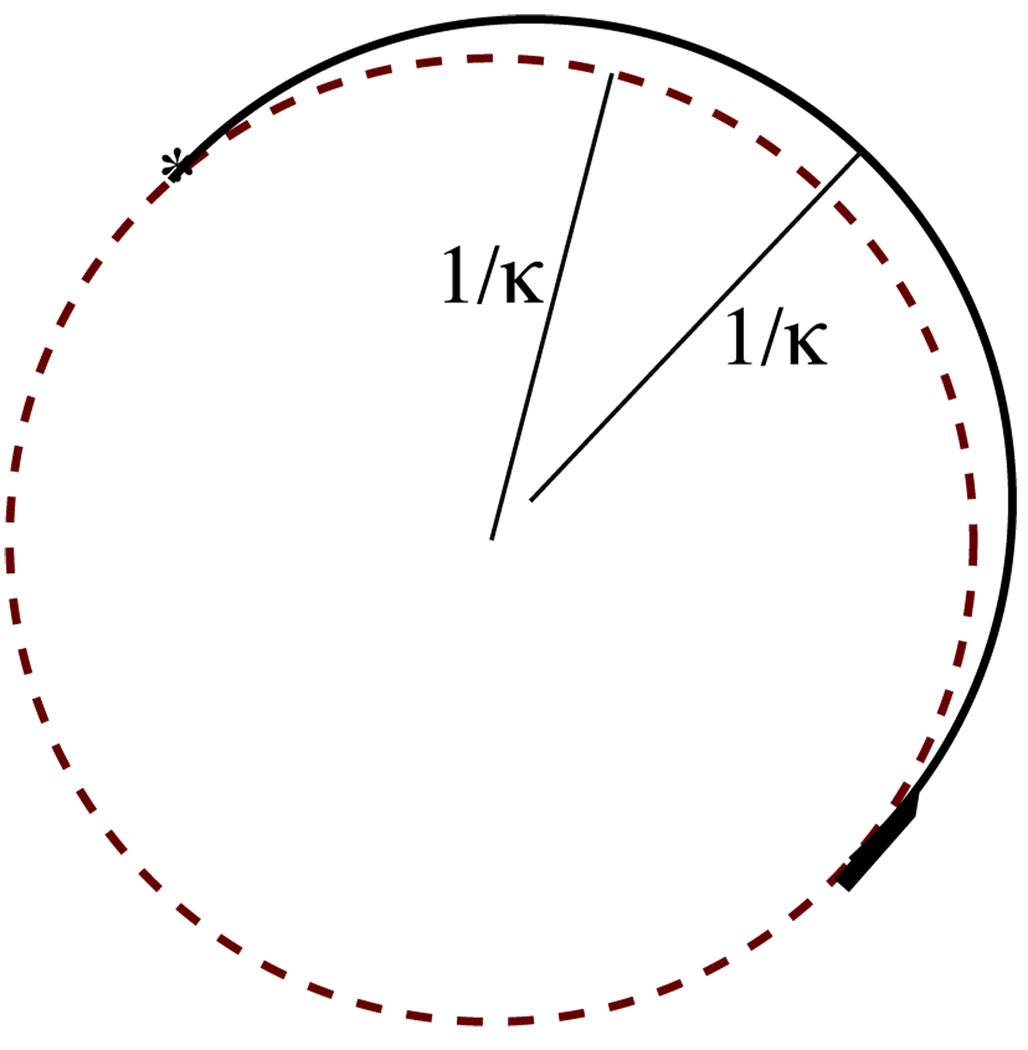
Fig. 3.

Small-time local controllability fails even for tracking a natural trajectory of the needle, a circle (green, dashed) of radius 1/κ. Here, a small initial perturbation in heading of the needle (black, solid) is depicted. The radius of curvature of the actual needle trajectory can never be less than 1/κ, and thus even for the smallest possible perturbation of the needle heading, the needle must travel at least π/κ before re-intersecting (*) the desired path. Pitching out of the plane of the circle only exacerbates this issue, and the problem cannot be overcome with control or replanning.