Figure 2.

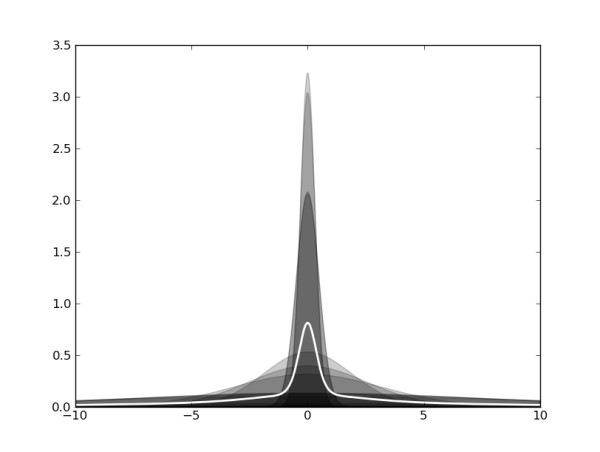
Modeling non-rigid displacements by scale mixtures. Our model for the distribution of displacement vectors is a mixture of isotropic Gaussians with increasing width (grey filled curves). By averaging of the Gaussians, we obtain a heavy-tailed effective distribution (white line) that exhibits a narrow central peak and broad tails. By adding more and more components one achieves in the limit of infinitely many components an exact representation of the heavy-tailed distribution. In this limit, the average is obtained as an integral over Gaussians of continuously varying width. How the widths are distributed is governed by a density function g(s) of the scales or inverse widths s. The functional form of the mixing distribution and of the implied heavy-tailed model is govern by the shape and scale parameters α and β.