Generalized Functional Linear Models with Semiparametric Single-Index Interactions

Abstract

We introduce a new class of functional generalized linear models, where the response is a scalar and some of the covariates are functional. We assume that the response depends on multiple covariates, a finite number of latent features in the functional predictor, and interaction between the two. To achieve parsimony, the interaction between the multiple covariates and the functional predictor is modeled semiparametrically with a single-index structure. We propose a two step estimation procedure based on local estimating equations, and investigate two situations: (a) when the basis functions are pre-determined, e.g., Fourier or wavelet basis functions and the functional features of interest are known; and (b) when the basis functions are data driven, such as with functional principal components. Asymptotic properties are developed. Notably, we show that when the functional features are data driven, the parameter estimates have an increased asymptotic variance, due to the estimation error of the basis functions. Our methods are illustrated with a simulation study and applied to an empirical data set, where a previously unknown interaction is detected. Technical proofs of our theoretical results are provided in the online supplemental materials.

1 Introduction

In this paper, we are interested in functional data analysis for regression problems with a scalar response and where some of the covariates are functional. The most important model for such problems is the functional generalized linear model, where the response depends on a linear projection of the functional predictor. Some recent work on this problem includes Ramsay and Silverman (2005), Müller and Stadtmüller (2005), Yao, Müller and Wang (2005), Cardot and Sarda (2005), Cai and Hall (2006), Ferraty and Vieu (2006), Crainiceanu, Staicu and Di (2008) and Di, Crainiceanu, Caffo and Punjabi (2009), among many others.

However, most existing work does not readily accommodate the existence of an interaction between the functional predictor and other covariates. Our paper addresses this issue by introducing a novel class of models that accommodate such an interaction. A special feature of our work, which differs from the existing literature, is that we use a semiparametric single index structure to model the potential interaction between the functional predictor and other covariates. This single index structure not only gives flexibility in describing a complex interaction when there are two or more other covariates but it also allows us to propose a practically feasible two-stage procedure to address estimation and inference issues.

Our new generalized functional linear models with semiparametric interactions have the structure that the response depends on latent features of the functional data and their interaction with other possibly multivariate covariates. The “features” in functional data that we are considering are the projections of the functional data onto orthonormal basis functions. These basis functions can be either fixed, e.g., Fourier or wavelet basis functions, or data driven, e.g., principal components. The interaction is modeled semiparametrically, with the regression coefficient function for the functional predictor depending on a single-index function of the multivariate covariates.

After defining the modeling framework in Section 2, we split our study into two tracks. In the first track, in Section 3, we consider the situation that the functional predictor is fully observed and the basis functions are pre-determined, as might occur for Fourier basis functions or some versions of splines. Consequently, the score of the latent features can be evaluated. In this context we propose a backfitting estimation procedure based on local estimating equations. The procedure we propose consists of two stages, which are based on the philosophy of minimum average variance estimation (MAVE, Xia, Tong, Li and Zhu, 2002): in the first stage, we use multivariate kernel weights in the local estimating equations to get consistent initial values; in the second stage, we switch to univariate kernel methods to achieve more efficient estimators. We also derive the asymptotic properties of the methodology.

The second track of the paper, in Section 4, considers the case that the functional features/basis functions are data driven and need to be estimated. At present, the most common dimension reduction device in functional data analysis is functional principal component analysis (FPCA). Some recent work, including Yao, et al. (2005), Hall and Hosseini-Nasab (2006) and Hall, Müller and Wang (2006), have led to a deeper understanding of this method and its properties. We apply the FPCA method based on kernel smoothing as proposed by the authors mentioned above, and then plug the estimated PCA scores into the two stage estimation procedure of Section 3. With the assumption that the number of observations per curve goes to infinity at a sufficient rate, we show that the estimators of the proposed models are still root-n consistent and asymptotically normally distributed. An important finding is that, even when there is sufficient number of observations per curve, the estimation error in FPCA will increase the variance of the final estimator of the functional linear model. This fact is not sufficiently well appreciated in the literature.

We illustrate the numerical performance of our procedure in a simulation study given in Section 5, and by an empirical application to colon carcinogenesis data, where we exhibit a previously unknown interaction. Final remarks are provided in Section 6, and all proofs are sketched in the Web Appendix, which is available in the online supplemental materials.

2 Model and Data Structure

The data consist of i = 1, …, n independent triples (Y_i, X_i, Z_i), where Y is the response, X is a longitudinal covariate process and Z denotes other covariates. Following Carroll, Fan, Gijbels and Wang (1997) and Müller and Stadtmüller (2005), we model the relationship between Y and {X(·),Z} by imposing structures on the conditional mean and variance of Y. The key component of the mean function is a semiparametric functional linear model where the functional coefficient function varies with both t and Z. More precisely, if E(Y | X, Z) = μ_Y (X, Z), the model is

$$\begin{array}{c}g\{{\mu }_Y(X,\mathit{Z})\}={\displaystyle {\int }_{𝒯}𝔄(t,{\mathit{Z}}_1)X(t)\mathit{\text{dt}}+{\mathit{\beta }}^{\mathrm{T}}}\mathit{Z};\hfill \\ \text{ var}(Y|X,\mathit{Z})={\sigma }_Y^{2}V\{{\mu }_Y(X,\mathit{Z})\},\hfill \end{array}$$ (1)

where g(·) and V(·) are known functions, 𝔄(·,Z₁) and β are unknown and 𝒯 = [a, b] is a fixed interval. We allow the coefficient function 𝔄(·, ·) to depend on a covariate vector Z₁ which is a subset of Z.

Suppose ψ₁(t), ψ₂(t), ⋯, ψ_p(t) are p orthonormal functions on 𝒯 , and ξ_j = ∫ ψ_j(t){X(t) − μ_X(t)}dt, for j = 1, ⋯, p, where μ_X(t) = E{X(t)}. It is commonly assumed that the conditional distribution of Y given X (·) and Z only depends on ξ = (ξ₁, ⋯, ξ_p)^T and Z. There are two typical structural considerations in functional data analysis, the two tracks of our research. The first track is that of fixed features, where the (ψ_j) are known basis functions, such as Fourier basis functions. Recently Zhou, Huang and Carroll (2008) also showed how to construct an orthonormal basis from B-splines. The second track is of a data-driven nature, e.g., the (ψ_j) are the leading principal components of X(t). The choice of p, as well as the choice of basis functions, is in many cases quite subjective. If we further assume a likelihood function for the data, we can choose p by an AIC criterion, similar to that in Müller and Stadtmüller (2005) and Yao et al. (2005). Because of limited space, such a model selection problem will not be fully explored in this paper.

By assumption, Y depends on X (·) only through the features ξ. Let ψ(t) = {ψ₁(t), ⋯, ψ_p(t)}^T. To make the model parsimonious without imposing strong parametric structural assumptions, and to allow interactions between X and Z₁, we further assume that

$$𝔄(·,{\mathit{Z}}_1)={\mathit{\psi }}^{\mathrm{T}}(t)\mathit{\alpha }({\mathit{Z}}_1;\mathit{\theta }),\text{and that }\mathit{\alpha }({\mathit{Z}}_1;\mathit{\theta })={\mathit{\alpha }}_1+\mathit{S}({\mathit{Z}}_1;\mathit{\theta }){\mathit{\alpha }}_2,$$ (2)

where S(Z₁; θ) is a semiparametric function with a single-index structure described below, and (α₁;α₂) are unknown coefficient vectors. Thus, we assume that the interaction between the longitudinal process X(t) and the multivariate Z is modeled through a single index function of the multivariate covariate Z₁.

For interpretation of such interaction, we focus on a given ψ_j(t). For this ψ_j(t), the value of ξ_ij determines whether the X variable of subject i has elevated values in this direction. The parameters, α_2j, θ and S(·), determine how the variable Z_i interacts with X in this direction through the values of α_2jξ_ijS(Z_1i; θ). When Z₁ is scalar, S(Z₁) is a nonparametric function. When Z₁ is a d₁ × 1 vector, S(Z₁; θ) = S(θ^TZ₁), where θ = (θ₁, ⋯, θ_d1)^T is a single-index weight vector subject to the usual single-index constraints ‖θ‖ = 1 and θ₁ > 0. To ensure identifiability, we set the additional constraints that ‖α₂‖² = 1 and E{S(Z₁; θ)} = 0.

Our model is innovative and flexible in the following ways. First, when S(z; θ) ≡ 0 for all z, model (1) yields the functional generalized linear model of Müller and Stadmüller (2005) as a special case. Second, the nonparametric function S(·) enables us to model nonlinear interactions flexibly while the single-index θ^TZ₁ allows us to accommodate a multivariate Z₁ without suffering from the curse of dimensionality. Third, the model we propose is not limited to functional data. Given the latent variables ξ, the conditional mean of Y can be simplified to

$$g^{-1}\{\mathrm{E}(Y|\mathit{\xi },\mathit{Z})\}={\mathit{\alpha }}^{\mathrm{T}}({\mathit{Z}}_1;\mathit{\theta })\mathit{\xi }+{\mathit{\beta }}^{\mathrm{T}}\mathit{Z}.$$ (3)

Therefore, our semiparametric interaction model is readily applicable to multivariate data, where ξ is an observed covariate vector.

3 Model Estimation With Fixed Basis Functions

In this section, we consider the case that the basis functions (ψ_j) are known, X_i(t) is fully observed and centered, and consequently ξ_ij = ∫ X_i(t)ψ_j(t)dt is known.

We study this seemingly unrealistic scenario first for two reasons. First, this is a commonly used ideal situation typically considered first in the functional data literature in order to motivate new methodology. A more realistic situation will be studied in our Section 4. Second, as pointed out in the previous section, the semiparametric interaction model we proposed is not limited to functional data. The methods we propose below for this ideal situation are also applicable to the multivariate semiparametric model (3) when ξ is another observed multivariate covariate.

3.1 Local Quasi-likelihood estimation

We estimate S(·) through a local polynomial smoothing approach. Let $\mathbf{\Theta }={({\mathit{\alpha }}_1^{\mathrm{T}},{\mathit{\alpha }}_2^{\mathrm{T}},{\mathit{\beta }}^{\mathrm{T}},{\mathit{\theta }}^{\mathrm{T}})}^{\mathrm{T}}$. Our strategy is to iterate between estimating Θ while holding S(·) fixed and estimating S(·) via local estimating equations while holding Θ fixed.

Let Q(w, y) be the quasi-likelihood function satisfying ∂Q(w, y)/∂w = (y − w)/V (w) (McCullagh and Nelder, 1989). For a given value of Θ, we estimate S(υ) and S′(υ) by the argument (a₀, a₁)^T that minimizes the local quasi-likelihood

$${\displaystyle {\sum }_{i=1}^{n}Q\left(g^{-1}[{\mathit{\alpha }}_1^{\mathrm{T}}{\mathit{\xi }}_i+\{a_0+a_1({\mathit{\theta }}^{\mathrm{T}}{\mathit{Z}}_{i1}-\upsilon )\}{\mathit{\alpha }}_2^{\mathrm{T}}{\mathit{\xi }}_i+{\mathit{\beta }}^{\mathrm{T}}{\mathit{Z}}_i],Y_i\right)w_i(\upsilon ),}$$ (4)

where w_i(υ) is the local weight for the i^th observation.

Model (1) is new, although in various special cases it shares the spirit of previous work on single index models such as Carroll, et al. (1997), Xia et al. (2002) and Xia and Härdle (2006). For computation, we adopt the philosophy of the latter two papers, describing a version of their MAVE method applicable to our problem. Consider υ = θ^T Z_j1 in (4) for each j ∈ {1, ⋯, n} and let a_0j and a_1j be the estimate of S(θ^T Z_j1) and S′(θ^T Z_j1), respectively.

Summing over υ = θ^T Z_j1 for all j in (4) while holding the values of (a_0j, a_1j) fixed, and denoting Z_i1 − Z_j1 by Z_ij,1, we can now update the rest of the parameters by minimizing

$$𝒬={\displaystyle {\sum }_{j=1}^n{\displaystyle {\sum }_{i=1}^{n}Q\left[g^{-1}\{{\mathit{\alpha }}_1^{\mathrm{T}}{\mathit{\xi }}_i+(a_{0j}+a_{1j}{\mathit{\theta }}^{\mathrm{T}}{\mathit{Z}}_{\mathit{\text{ij}},1}){\mathit{\alpha }}_2^{\mathrm{T}}{\mathit{\xi }}_i+{\mathit{\beta }}^{\mathrm{T}}{\mathit{Z}}_i\},Y_i\right]}{w}_{\mathit{\text{ij}}},}$$ (5)

with respect to Θ, where w_ij are local weights specified in more detail below. As described above, for identifiability purposes we let θ and α₂ satisfy ‖θ‖ = 1 and ‖α₂‖ = 1. The constraint E{S(θ^T Z₁)} = 0 is replaced by $n^{-1}{\displaystyle {\sum }_{j=1}^n{a}_{0j}}=0$.

We have now restructured the estimation procedure into one that minimizes the local quasi-likelihood function (5) iteratively with respect to {a_0j, a_1j, j = 1, ⋯, n} and Θ. One remaining task is to specify the local weights w_ij. We use two sets of weights. In the initial stage, we let $w_{\mathit{\text{ij}}}^{[1]}=H_b({\mathit{Z}}_{\mathit{\text{ij}},1})/{\displaystyle {\sum }_{\ell =1}^n{H}_b({\mathit{Z}}_{\ell j,1})}$, where H(·) is a d₁-dimensional kernel function and H_b(·) = b^−d₁ H(·/b). This will enable us to find a consistent estimator Θ̃. We then switch to a set of refined weights to gain more efficiency. In the second stage, we carry out the same iteration steps but let $w_{\mathit{\text{ij}}}^{[2]}(\check{\mathit{\theta }})=K_h({\check{\mathit{\theta }}}^{\mathrm{T}}{\mathit{Z}}_{\mathit{\text{ij}},1})/{\displaystyle {\sum }_{\ell =1}^n{K}_h({\check{\mathit{\theta }}}^{\mathrm{T}}{\mathit{Z}}_{\ell j,1})}$, where K(·) is a univariate kernel function, K_h(·) is its scaled version, h is the bandwidth and θ̌ is the estimated value of θ from the previous iteration.

The estimation procedure then is as follows.

Stage 1 (Initial estimator) Iteratively update S(·) and Θ by minimizing (5) with $w_{\mathit{\text{ij}}}=w_{\mathit{\text{ij}}}^{[1]}$, until the values converge. At each update of the parameters, we adjust for the constraints, $\Vert {\mathit{\alpha }}_2\Vert =\Vert \mathit{\theta }\Vert =1\text{and}{n}^{-1}{\displaystyle {\sum }_{i=1}^n\mathit{S}({\mathit{\theta }}^{\mathrm{T}}{\mathit{Z}}_{i1})=0}$. We denote the converged values as Θ̃ and S̃(·). These are consistent estimators which will serve as initial values for Stage 2.

Stage 2 (Refined estimator) To improve efficiency, we replace the initial weights by $w_{\mathit{\text{ij}}}=w_{\mathit{\text{ij}}}^{[2]}(\tilde{\mathit{\theta }})$, where θ̃ is the consistent estimator of θ from Stage 1. The final estimators are denoted as Θ̂ and Ŝ(·).

In common with the MAVE procedure in Xia and Härdle (2006), the procedure described above does not require a root-n consistent pilot estimator of Θ, which is difficult to obtain in the functional data setting. We will show in Section 3.2 that the initial estimator using the multivariate kernel weights provides a consistent estimator, while the use of the univariate kernel weights with consistently estimated θ at Stage 2 yields a more efficient asymptotically normally distributed estimator.

In practice, we use a one-step Newton-Raphson update version of the iterative algorithm in Stages 1 and 2, which speeds up the computation considerably. As shown in our proofs for Theorem 1 and 2, the iterations in each stage generate a self-attraction process; that is, asymptotically, the distance between the current and previous estimates of Θ shrinks to zero along with the iteration. This is one of the standard ways to show convergence properties of an iterative algorithm. It is also used by Xia and Härdle (2006) in a setup simpler than ours. In practice, with n being finite, an algorithm with this asymptotic convergence property could still fail to converge. We have not encountered such numerical difficulties in our study though. We have provided more details about the algorithm in the web supplement.

3.2 Asymptotic Theory

Denote the true parameter as Θ₀, and the true interaction link function as S₀(·). Following the notation in Carroll et al. (1997), let q₁(x, y) = {y − g⁻¹(x)}ρ₁(x) and $q_2(x,y)=\{y-g^{-1}(x)\}{\rho }_1^{\prime }(x)-{\rho }_2(x)$, where ρ_ℓ(x) = {dg⁻¹(x)/dx}^ℓ/V{g⁻¹(x)}, ℓ = 1, 2. As mentioned previously, here we assume the (ξ_ij) are known. Estimation of ξ_ij and the effect of the estimation error will be discussed in Section 4. We make the following assumptions.

Assumption (C1)

• (C1.1)The marginal density of Z₁ is positive and uniformly continuous, with a compact support 𝒟 ∈ ℝ ^d₁. Let $𝒰={\mathit{\theta }}_0^{\mathrm{T}}{\mathit{Z}}_1$ be the true single-index, with a density f_𝒰(u). Assume f_𝒰 is twice continuously differentiable.
• (C1.2)g⁽³⁾ (·) and V⁽²⁾ (·) exist and are continuous.
• (C1.3)S₀(·) is twice continuously differentiable.
• (C1.4)For all x, ρ₂(x) > 0 and dρ₂(x)/dx is bounded.

Assumption (C2)

• (C2.1)H (·) is a symmetric d₁ dimensional probability density function, ∫ H (x)xx^Tdx = I. b → 0, log(n)/(nb^d₁+2) → 0.
• (C2.2)V₁ (z; Θ, S), V₂(z; Θ, S) and V₃(z; Θ, S) defined in Web Appendix B.1 are twice continuously differentiable in z, and Lipschitz continuous in Θ.

Assumption (C3)

• (C3.1)K(·) is a symmetric univariate probability density function, with support on [−1, 1], ${\sigma }_K^2={\displaystyle \int u^{2}K(u)\mathit{\text{du}},{\kappa }_2={\displaystyle \int K^2(u)\mathit{\text{du}}.h}}~n^{-\lambda },1/6<\lambda <1/4$.
• (C3.2)𝒱₁(z; θ), 𝒱₂(z; θ) and 𝒱₃(z; θ) in Web Appendix B.2 are twice continuously differentiable in z, and Lipschitz continuous in θ.

Here are the two main results in this section.

THEOREM 1 (Consistency of the initial estimator) Under conditions (C1)–(C3), ‖Θ̃−Θ₀‖ → 0 with probability 1.

THEOREM 2 (Asymptotic normality of the refined estimator) Under conditions (C1)–(C3),

$$\begin{array}{c}\sqrt{n}(\widehat{\mathbf{\Theta }}-{\mathbf{\Theta }}_0)\to \text{Normal}(\mathbf{0},{𝒜}^{-}ℬ{𝒜}^{-}),\hfill \\ \sqrt{nh}\{\widehat{\mathit{S}}(u)-{\mathit{S}}_0(u)-h^2{\mathit{S}}_0^{(2)}(u){\sigma }_k^2/2\}\to \mathit{\text{Normal}}\{0,{\sigma }_{\mathit{S}}^2(u)\},\hfill \\ \hfill \\ \hfill \\ \hfill \end{array}$$

where 𝒜 and ℬ are defined in the Appendix, ${\sigma }_{\mathit{S}}^2(u)={\kappa }_2\mathrm{E}\{({\mathit{\alpha }}_{2,0}^{\mathrm{T}}{\mathit{\xi }}_i){\in }_i^2|{\mathit{\theta }}_0^{\mathrm{T}}{\mathit{Z}}_{i1}=u\}/\{{\sigma }_{\upsilon }^4(u)f_{𝒰}(u)\},{\sigma }_{\upsilon }^2(u)=\mathrm{E}\{{\rho }_2({\eta }_i){({\mathit{\alpha }}_{2,0}^{\mathrm{T}}{\mathit{\xi }}_i)}^2|{\mathit{\theta }}_0^{\mathrm{T}}{\mathit{Z}}_{i1}=u\}$.

Remark: The algorithm we use is similar to the MAVE method (Xia et al. 2002), which is a relatively new development in the literature on backfitting methods. Unlike many other back-fitting algorithms, the method we are using does not require any artificial undersmoothing for the nonparametric function S(·), see our condition (C3.1) on the rate of the bandwidth. The method also differs from the algorithm in Carroll et al. (1997) in that we do not need a root-n consistent pilot estimator for the parametric components using approaches such as Sliced Inverse Regression (Li, 1991). Instead, the initial estimator in Stage 1 of our procedure will provide a consistent pilot estimator. The refined approach in Stage 2 further results in an efficiency gain which is mainly contributed by a faster convergence rate in the nonparametric estimation at this stage. An efficiency gain due to the equivalent reason by switching to refined kernel weights in Stage 2 was documented by Xia and Härdle (2006) for partially linear single-index models; see also Section 5.1 where we illustrate this numerically.

4 Estimation With Principal Components

4.1 Background

The most popular dimension reduction method in functional data analysis is principal component analysis, leading to estimated basis functions. Here we focus on the common scenario in which ψ_j(t) denotes the eigenfunction in functional principal component analysis. For the longitudinal process {X(t), t ∈ 𝒯} with mean function μ_X (t), the covariance function is R(s, t) = cov{X(s), X (t)} with eigen-decomposition $R(s,t)={\displaystyle {\sum }_{j=1}^{\infty }{\omega }_j{\psi }_j(s){\psi }_j(t)}$, where the ω_j are the non-negative eigenvalues of R(·, ·), which, without loss of generality, satisfy ω₁ > ω₂ > ⋯ > 0, and the ψ_j’s are the corresponding eigenfunctions. The Karhunen-Loève expansion of X (t) is

$$X(t)-{\mu }_X(t)={\displaystyle {\sum }_{j=1}^{\infty }{\xi }_j{\psi }_j(t),}$$ (6)

where ξ_j = ∫ ψ_j(t){X(t) − μ_X(t)}dt has mean zero, with cov(ξ_j, ξ_k) = I (j = k)ω_j.

Under this framework, our model (1) means that Y is dependent on the leading p principal components in X(·). The reason that we assume that only a finite number of PC’s are relevant is that, in functional data that is commonly seen in biological applications, estimation of high order PC’s is highly unstable and difficult to interpret, see the comments in Rice and Silverman (1991) and Hall, et al. (2006). Yao et al. (2005) proposed to use an AIC criterion to choose p. Even though, to the best of our knowledge, there is no theoretical support behind the use of AIC in the existing literature, we found it a very sensible criterion in our numerical investigations which we have reported in Section 5. We made a slight modification of their method in terms of counting the number of parameters, and at least in our simulations were able to select the correct number of PC in every case. More work on this general topic clearly needs to be done.

It often happens that the covariate process we observe contains additional random errors and instead we observe

$$W_{\mathit{\text{ij}}}=X_i(t_{\mathit{\text{ij}}})+U_{\mathit{\text{ij}}},j=1,\cdots ,m_i,$$ (7)

where U_ij are independent zero-mean errors, with $\text{var}\{U_i(t)\}={\sigma }_u^2$, and the U_ij are also independent of X_i(·) and Z_i.

4.2 Principal Components Analysis via Kernel Smoothing

Many functions and parameters in the expressions given above can be estimated from the data. Thus, μ_X(·) and R(·, ·) can be estimated by local polynomial regression, and then ψ_k(·), ω_k and ${\sigma }_u^2$ can be estimated using the functional principal component analysis method proposed in Yao, et al. (2005) and Hall, et al. (2006). We now briefly describe the method. We first estimate μ_X(·) by a local linear regression, μ̂_X(t) = â₀ where

$$({\widehat{a}}_0,{\widehat{a}}_1)={\text{argmin}}_{a0,a1}{\displaystyle {\sum }_{i=1}^n{\displaystyle {\sum }_{j=1}^{m_i}{\{W_{\mathit{\text{ij}}}-a_0-a_1(t_{\mathit{\text{ij}}}-t)\}}^{2}K\{t_{\mathit{\text{ij}}}-t)/h_{\mu }\},}}$$

K(·) is a kernel function and h_μ is the bandwidth for estimating μ_X. Letting ϖ_XX(s, t) = E{X(s)X(t)}, define ϖ̂_XX(s, t) = â₀, where (â₀, â₁, â₂) minimizes

$${\displaystyle {\sum }_{i=1}^n{\displaystyle {\sum }_{j=1}^{m_i}{\displaystyle {\sum }_{k\ne j}{\{W_{\mathit{\text{ij}}}{W}_{\mathit{\text{ik}}}-a_0-a_1(t_{\mathit{\text{ij}}}-s)-a_2(t_{\mathit{\text{ik}}}-t)\}}^2}K\left(\frac{t_{\mathit{\text{ij}}}-s}{h_{\varpi }}\right)K\left(\frac{t_{\mathit{\text{ik}}}-t}{h_{\varpi }}\right)}.}$$

Then R̂(s, t) = ϖ̂_XX(s, t) − μ̂_X(s)μ̂_X(t). The (ω_k) and {ψ_k(·)} can be estimated from an eigenvalue decomposition of R̂(·, ·) by discretization of the smoothed covariance function, see Rice and Silverman (1991) and Capra and Müller (1997). By realizing that ${\sigma }_w^2(t)=\text{var}\{W(t)\}=R(t,t)+{\sigma }_u^2$, we let ${\widehat{\sigma }}_w^2(t)={\widehat{a}}_0-{\widehat{\mu }}_X^2(t)$, where (â₀, â₁) minimizes

$${\displaystyle {\sum }_{i=1}^n{\displaystyle {\sum }_{j=1}^{m_i}{\{W_{\mathit{\text{ij}}}^2-a_0-a_1(t_{\mathit{\text{ij}}}-t)\}}^{2}K\{t_{\mathit{\text{ij}}}-t)/h_{\sigma }\},}}$$

and ${\sigma }_u^2$ is estimated by ${\widehat{\sigma }}_u^2={(b-a)}^{-1}{\displaystyle {\int }_a^b\{{\widehat{\sigma }}_w^2(t)-\widehat{R}(t,t)\}}\mathit{\text{dt}}$.

There are two ways to predict the principal component scores, ξ_ik. The first is the PACE method proposed by Yao, et al. (2005). By assuming the covariate process X_i(t) and the measurement errors U_ij are jointly Gaussian, one can show that the conditional expectation of ξ_ij given W_i = (W_i1, ⋯, W_i,mi)^T is ${\tilde{\xi }}_{\mathit{\text{ik}}}={\omega }_k{\psi }_{\mathit{\text{ik}}}{\displaystyle {\sum }_{W_i}^{-1}({\mathit{W}}_i-{\mathit{\mu }}_{Xi})}$, where ψ_ik = {ψ_k(t_i1), ⋯, ψ_k(t_i,mi)}^T, μ_Xi = {μ_X(t_i1), ⋯, μ_X(t_i,mi)}^T, and ${\sum }_{W_i}=\text{cov}({\mathit{W}}_i)={\{R(t_{\mathit{\text{ij}}},t_{\mathit{\text{ij}}\prime })+{\sigma }_u^{2}I(t_{\mathit{\text{ij}}}=t_{\mathit{\text{ij}}\prime })\}}_{j,j\prime =1}^{m_i}$. The PACE predictors of the principal component scores are calculated by plugging the kernel estimates into the conditional expectation expression,

$${\widehat{\xi }}_{\mathit{\text{ik}}}={\widehat{\omega }}_k{\widehat{\mathit{\psi }}}_{\mathit{\text{ik}}}{\widehat{\mathrm{\Sigma }}}_{W_i}^{-1}({\mathit{W}}_i-{\widehat{\mathit{\mu }}}_{\mathit{\text{Xi}}}).$$ (8)

An alternative method is by numerical integration. Motivated by the definition that ξ_ik = ∫{X_i(t) − μ_X(t)}ψ_k(t)dt, we define

$${\widehat{\xi }}_{\mathit{\text{ik}}}={\displaystyle \sum _{j=2}^{m_i}\{W_{\mathit{\text{ij}}}-{\widehat{\mu }}_x(t_{\mathit{\text{ij}}})\}{\widehat{\psi }}_k(t_{\mathit{\text{ij}}})(t_{\mathit{\text{ij}}}-t_{i,j-1}).}$$ (9)

In our numerical experience, when we have densely sampled functional data, i.e. m_i is large and the t_ij’s are evenly spread in the interval [a, b], the two predictors given in (8) and (9) have comparable performance. The outcomes of the numerical integral predictor, which is easier to use in our theoretical justifications, are reported in Section 5.

4.3 Asymptotic Results for Plugging-in Estimated PC

In this section, we study the asymptotic properties of the estimators proposed in Section 3 when the principal component scores are replaced by their estimates. Without loss of generality, we assume that μ_X (t) = 0, and that there are the same number of discrete observations for each subject, i.e. m_i = m for all i. Throughout, we assume that m → ∞. We will first focus on the properties of the initial estimators that are obtained at the end of Stage 1. We then provide conditions and the corresponding asymptotic properties of the refined estimators.

4.3.1 Properties of the initial estimators

Assumption (C4)

• (C4.1)(Hall, et al., 2006) The process X(·) is independent of the measurement error U in (7), E(U) = 0 and $\text{var}(U)={\sigma }_u^2$. For some c > 0, ${\text{max}}_{j=0,1,2}\mathrm{E}\left\{{\text{ sup}}_{t\in 𝒯}|X^{(j)}(t){|}^c\right\}+\mathrm{E}(|U{|}^c)<\infty$.
• (C4.2)We have ω₁ > ω₂ > ⋯ > ω_p > ω_p+1 ≥ 0 and ϕ_k is twice continuously differentiable on 𝒯, for k = 1, ⋯, p.
• (C4.3)The t_ij are equally spaced in 𝒯, i.e. t_ij = a + (j/m) × (b − a), for j = 1, ⋯, m. m → ∞.
• (C4.4)h_ϖ ~ n^−λ_ϖ , 1/4 < λ_ϖ < 1/3.

In Assumption (C4.3) we assume the (t_ij) are fixed and equally spaced, thus allowing convenient mathematical derivations. The conclusion of Lemma 1 holds for random designs. The proofs of the following lemma and theorem are provided in the Web Appendix.

LEMMA 1 Under Assumption (C4), $\Vert {\widehat{\psi }}_k-{\psi }_k\Vert =O_p\{h_{\varpi }^2+{({\mathit{\text{nh}}}_{\varpi })}^{-1/2}\}$, for k = 1, ⋯, p. Let ξ̂_ik be the estimated principal component score defined in (9). Then ξ̂_ik − ξ_ik = O_p(m^−1/2+n^−1/3) for i = 1, 2, ⋯, n, and k = 1, ⋯, p.

THEOREM 3 Suppose Θ̃ is the initial estimator of Θ defined in Section 3, using the estimated principal component scores. Assume that the bandwidth b for the multivariate kernel satisfies mb → ∞. Under conditions (C1), (C2) and (C4), ‖Θ̃ − Θ₀‖ → 0 with probability 1.

4.3.2 Properties of the Refined Estimators

In this subsection we will discuss the scenario under which we can pretend that we know the entire trajectory of X_i(·). More precisely, we give conditions that ensure that the smoothing errors are asymptotically negligible. Consequently, we can smooth each curve and effectively eliminate effects from the measurement error in (7). Such a “smooth first, then perform estimation” procedure was considered and justified by Zhang and Chen (2007) in the functional linear model setting.

Let X̃_i (t) be the estimated trajectory of X_i(t), i.e., the outcome of applying local linear smoothing to W_i. Let h_X be the bandwidth for smoothing each curve. Without loss of generality, assume the X̃_i(t) have been centered, i.e., the mean curve was subtracted out from each estimated trajectory. One can estimate the covariance function by $\tilde{R}(s,t)=n^{-1}{\displaystyle {\sum }_{i=1}^n{\tilde{X}}_i(s){\tilde{X}}_i(t)}$. One can also estimate the eigenfunctions by an eigen-decomposition of R̃, and the principal component scores by ${\widehat{\xi }}_{\mathit{\text{ik}}}={\displaystyle {\int }_a^b{\tilde{X}}_i(t){\widehat{\psi }}_k(t)\mathit{\text{dt}}}$. Zhang and Chen (2007) showed in their Theorem 4 that when sampling points are sufficiently dense on each curve, the principal component analysis method given above is asymptotically equivalent to knowing the entire trajectory of each X_i.

Assumption (C5)

• (C5.1)𝒢(t₁, t₂, t₃, t₄) = E{X(t₁)X(t₂)X(t₃)X(t₄)} − R(t₁, t₂)R(t₃, t₄) exists for all t_j ∈ 𝒯.
• (C5.2)We have m ≥ Cn^κ, with κ > 5/4.
• (C5.3)The t_ij are independent identically distributed random design points with density function f(·), where f is bounded away from 0 on 𝒯 and is continuously differentiable.
• (C5.4)h_X = O(n^−κ/5).

LEMMA 2 Let Ƶ (s, t) be a zero-mean Gaussian random field on {(s, t); s, t ∈ 𝒯}, with covariance function 𝒢 defined in Assumption (C5.1). Under assumptions (C4.1)–(C4.2) and (C5), $\Vert {\tilde{X}}_i-X_i\Vert =o_p(n^{-1/2}),\sqrt{n}(\tilde{R}-R)\to Ƶ$, and

$$\begin{array}{c}{\widehat{\psi }}_j(t)-{\psi }_j(t)=n^{-1/2}{\displaystyle {\sum }_{k\ne j}{({\omega }_j-{\omega }_k)}^{-1}{\psi }_k(t)}{\displaystyle \int Ƶ{\psi }_j{\psi }_k+o_p(n^{-1/2}),}\hfill \\ {\widehat{\xi }}_{\mathit{\text{ij}}}-{\xi }_{\mathit{\text{ij}}}=n^{-1/2}{\displaystyle {\sum }_{k\ne j}{\xi }_{\mathit{\text{ik}}}{({\omega }_j-{\omega }_k)}^{-1}}{\displaystyle \int Ƶ{\psi }_j{\psi }_k+o_p(n^{-1/2}).}\hfill \end{array}$$

The limit distribution of R̃ in Lemma 2 was given in Theorem 4 in Zhang and Chen (2007), whereas the last two equations are direct results of (2.8) of Hall and Hosseini-Nasab (2006).

By plugging in the estimated principal component scores, we have the following asymptotic results for the refined estimator defined in Section 3.

THEOREM 4 Let Θ̂ be the refined estimator with plugged in estimated PC scores. Under conditions (C1), (C3), (C4.1)–(C4.2) and (C5),

$$\sqrt{n}(\widehat{\mathbf{\Theta }}-{\mathbf{\Theta }}_0)\to \mathit{\text{Normal}}\{\mathbf{0},{𝒜}^{-}(ℬ+{ℬ}_1)A^{-}\},$$

where 𝒜, ℬ and ℬ₁ are defined in the Appendix. In addition, Ŝ(·) has the same asymptotic distribution as that in Theorem 2.

By comparing the asymptotic distributions in Theorem 2 and Theorem 4, we can clearly see the additional variation, ℬ₁, which is the consequence of the estimation error in the estimated principal components.

Remarks:

1. Taking the numerical integration method in (9) as an example, there are two sources of error in estimating FPCA scores: the first source is the prediction error for the PC scores given the true eigenfunctions; the second type of error is caused by plugging in the estimated eigenfunctions. Both sources of error tend to be ignored in the functional data literature.

2. One important contribution of our work is that we bring attention to the second source of error mentioned above. Even if we have all the information on each curve, the eigenfunction can only be estimated in a root-n rate (Hall and Hosseini-Nasab, 2006). This estimation error may seem to be small, but it affects PC score estimation in all subjects, and as illustrated in our theory this error will also affect the variance of the final estimator in regression.

3. Plugging in the predicted score is an idea similar to regression calibration (Carroll et al., 2006). With condition (C5.2), we basically assumed that the first type of error (prediction error for the PC scores given the true eigenfunctions) is negligible, which is a typical assumption in the functional data literature, see Müller and Stadtmüller (2005). This allows us to focus all attention on the second source of errors. Our model considers complex functional interactions and by its nature would need moderate to large sample sizes in order to reach sensible outcomes and reliable findings. When n and/or m are small, whether one could or should consider such a complex model is an interesting yet hard problem, which calls for future research.

4. When condition (C5.2) is violated, the first type of error described above will prevail. Since these prediction errors are independent among subjects, they are similar to the classical error in the measurement error literature and tend to cause bias in the final estimator. Therefore, whether m is sufficiently large can be empirically examined by checking the bias of the final estimator in a simulation study.

5 Numerical Studies

5.1 Logistic Regression Simulation Study

We performed a simulation study to illustrate the numerical performance of the proposed method. Our simulation setting resembles the empirical data described in Section 5.2. We generated the longitudinal process as a Gaussian process with mean function μ_X(t) = (t − 0.6)² − 0.1 for t ∈ [0, 1]. The covariance function of the process had 2 principal components, ${\psi }_1(t)=1,{\psi }_2(t)=\sqrt{2}\text{sin}(2\pi t)$, and the eigenvalues were ω₁ = 1 and ω₂ = 0.6. There were m = 30 discrete observations on each curve, with random observation time points being uniformly distributed on the interval [0, 1]. The measurements are contaminated with zero-mean Gaussian error with variance ${\sigma }_{\epsilon }^2=0.1$. We generated a binary response Y from the model $\text{pr}(Y=1|\mathit{Z},\mathit{\xi })=H\{{\mathit{\alpha }}_1^{\mathrm{T}}\mathit{\xi }+\mathit{S}({\mathit{\theta }}^{\mathrm{T}}{\mathit{Z}}_1){\mathit{\alpha }}_2^{\mathrm{T}}\mathit{\xi }+{\mathit{\beta }}^{\mathrm{T}}\mathit{Z}\}$, where H(η) = 1/{1 + exp(η)} is the logistic distribution function, $\mathit{Z}={(1,{\mathit{Z}}_1^{\mathrm{T}},Z_2)}^{\mathrm{T}},{\mathit{Z}}_1$ is a 2-dimensional random vector with a uniform distribution on [0, 1]², and Z₂ is a binary variable with pr(Z₂ = 1) = 0.5. We let ${\mathit{\alpha }}_1={(0.8,-1)}^{\mathrm{T}},{\mathit{\alpha }}_2={(1/\sqrt{2},1/\sqrt{2})}^{\mathrm{T}},\mathit{\theta }={(1/\sqrt{2},1/\sqrt{2})}^{\mathrm{T}}$, and β = (−1, 2, −2, 2). We let S(·) be a sine bump function similar to that used in Carroll et al. (1997), S(t) = 2sin{(t − c₁)/(c₂ − c₁)}, where $c_1=1/\sqrt{2}-1.645/\sqrt{12}\text{and}{c}_2=1/\sqrt{2}+1.645/\sqrt{12}$. We then standardized according to the constraints, which resulted in the true α₁ being ${\mathit{\alpha }}_1^{*}={\mathit{\alpha }}_1+\mathrm{E}\{\mathit{S}({\mathit{\theta }}^{\mathrm{T}}{\mathit{Z}}_1)\}{\mathit{\alpha }}_2$.

We set n = 500 and repeated the simulation 200 times. For each simulated data set we performed FPCA and fit the model using the algorithm described in Section 3, where ξ_ik was predicted by the direct numerical integral predictor. We obtained almost identical outcomes using the PACE predictor (not reported). For the iteration procedure, we declared convergence if max_k|Θ̃_k,curr − Θ̃_k,prev| is less than a pre-determined value, 10⁻⁶, where Θ̃_k,prev and Θ̃_k,curr denote the previous and current value of the k-th component of Θ̃. The number of principle component, p, was determined using AIC with the total number of parameters in the penalty equal to the number of PC scores.

The Monte Carlo (MC) means, standard deviations (SD) and biases of the refined estimator are presented in Table 1. All estimates behaved reasonably well. The comparisons of the MC biases and the MC SD’s indicate that the proposed estimator has a relatively smaller bias than the standard error. This seems to confirm the theoretical results that they are asymptotically unbiased. For all simulated data sets, the AIC criterion selected p = 2 which is the correct number of components. To confirm the efficiency gain of our refined estimator Θ̂ over the initial estimator Θ̃, we made a comparison of the mean squared error (MSE) of the two estimators. We found that MSE(Θ̃)/MSE(Θ̂) = 1.34. In other words, we have 34% efficiency gain by switching to refined kernel weights.

Table 1.

Estimation results for the simulation study. The reduced model is misspecified because it does not include the interaction, and the biases observed in the reduced model are thus to be expected.

		Full Model				Reduced Model
		MC	MC	MC		MC	MC	MC
	Truth	Mean	SD	Bias		Mean	SD	Bias
β0	−1	−1.0368	0.4181	−0.0368	β0	−0.9381	0.3681	0.0619
β1	2	2.0608	0.4925	0.0608	β1	1.7558	0.4289	−0.2442
β2	−2	−2.0197	0.4673	−0.0197	β2	−1.7400	0.4057	0.2600
β3	2	2.0744	0.2993	0.0744	β3	1.8869	0.2705	−0.1131
${\alpha }_{11}^{*}$	1.7986	1.7525	0.1932	−0.0461	α1	1.4958	0.1702	−0.3028
${\alpha }_{12}^{*}$	−0.0014	−0.0927	0.2009	−0.0913	α1	−0.1626	0.1796	−0.1612
α21	0.7071	0.6861	0.1887	−0.0210
α22	0.7071	0.6566	0.2511	−0.0505
θ1	0.7071	0.7012	0.1171	−0.0059
θ2	0.7071	0.6935	0.1177	−0.0136

^*Because of the identifiability issue with α₁, the version of α₁ that the algorithm estimates is ${\mathit{\alpha }}_1^{*}={\mathit{\alpha }}_1+\mathrm{E}\{\mathit{S}({\mathit{\theta }}^{\mathrm{T}}{\mathit{Z}}_1)\}{\mathit{\alpha }}_2$.

We compare the proposed approach to two other alternatives. First, we fit a misspecified reduced model without interactions, where $P(Y=1|\mathit{Z},\mathit{\xi })=H({\mathit{\alpha }}_1^{\mathrm{T}}\mathit{\xi }+{\mathit{\beta }}^{\mathrm{T}}\mathit{Z})$. The results are reported in Table 1. An immediate observation is elevated biases in the estimates of α₁ and β due to the misspecification of the model by not considering the interaction.

To assess the variation-inflation effect due to the PC scores being predicted, we also fit the model using the true principal component scores and compare the variances of the final estimators with those in Table 1. In Table 2, we present the relative variance inflation factor for using the true PC scores, which is defined as the ratio of the variance for each parameter when estimating the FPCA scores to the variance when the true FPCA scores are known. One clearly sees that the relative variance inflation factors are uniformly greater than one, with the highest inflation occurring for the coefficients of the second principal component, α₁₂ and α₂₂. This phenomena can be explained by the fact that the second PC is much harder to estimate than the first.

Table 2.

Variance inflation factors for using the true FPCA scores versus estimating them in the simulation study of Section 5. Displayed are the ratio of the variance for each parameter when estimating the FPCA scores to the variance when the true FPCA scores are known.

Parameter	Variance Inflation Factor
β0	1.08
β1	1.01
β2	1.01
β3	1.00
α11	1.00
α12	1.40
α21	1.10
α22	1.63
θ1	1.04
θ2	1.04

5.2 Colon Carcinogenesis Example

5.2.1 Background

The colon carcinogenesis data that we are using are similar to those analyzed in Morris et al. (2001, 2003), Li et al. (2007) and Baladandayuthapani et al. (2008). The biomarker of interest in this experiment is p27, which is a protein that inhibits the cell cycle. We used 12 rats randomly assigned to 2 diet groups (corn oil diet or fish oil diet) and 2 treatment groups (with/without butyrate supplement). Each rat was injected with a carcinogen, and then sacrificed 24 hours after the injection.

Beneath the colon tissue, there are pore structures called ‘colonic crypts’. A crypt typically contains 25 to 30 cells, lined up from the bottom to the top. The stem cells are at the bottom of the crypt, where daughter cells are generated. These daughter cells move towards the top as they mature. We sampled about 20 crypts from each of the 12 rats. The p27 expression level was measured for each cell within the sampled crypts. As previously noted in the literature (Morris et al. 2001, 2003), the p27 level measurements in the logarithm scale are natural functional data, since they are indexed by the relative cell location within the crypt. We have m = 25–30 observations (cells) on each function. In the literature, it has been noted that there is spatial correlation among the crypts within the same rat (Li et al., 2007, Baladandayuthapani et al., 2008). In this experiment, we sampled crypts sufficiently far apart so that the spatial correlations are negligible, and thus we can assume that the crypts are independent.

In this example, the response Y is the fraction of cells undergoing apoptosis (programmed cell death) in each crypt, to which we applied the usual arcsine-square root transformation. The functional data X(t) is the p27 level of a cell at relative location t. Write s₀ = 1, s₁ = indicator of a fish oil diet, s₂ = indicator of butyrate supplementation, and s₃ = mean proliferation level. Then ${\mathit{Z}}_1={(s_1,s_2,s_3)}^{\mathrm{T}},\mathit{Z}={(s_0,{\mathit{Z}}_1^{\mathrm{T}})}^{\mathrm{T}}$ and Z^Tβ = β₀ + s₁β_fish + s₂β_buty + s₃β_prolif. Similarly, S(Z₁, θ) = S(s₁θ_fish + s₂θ_buty + s₃θ_prolif).

5.2.2 Initial Model Fits

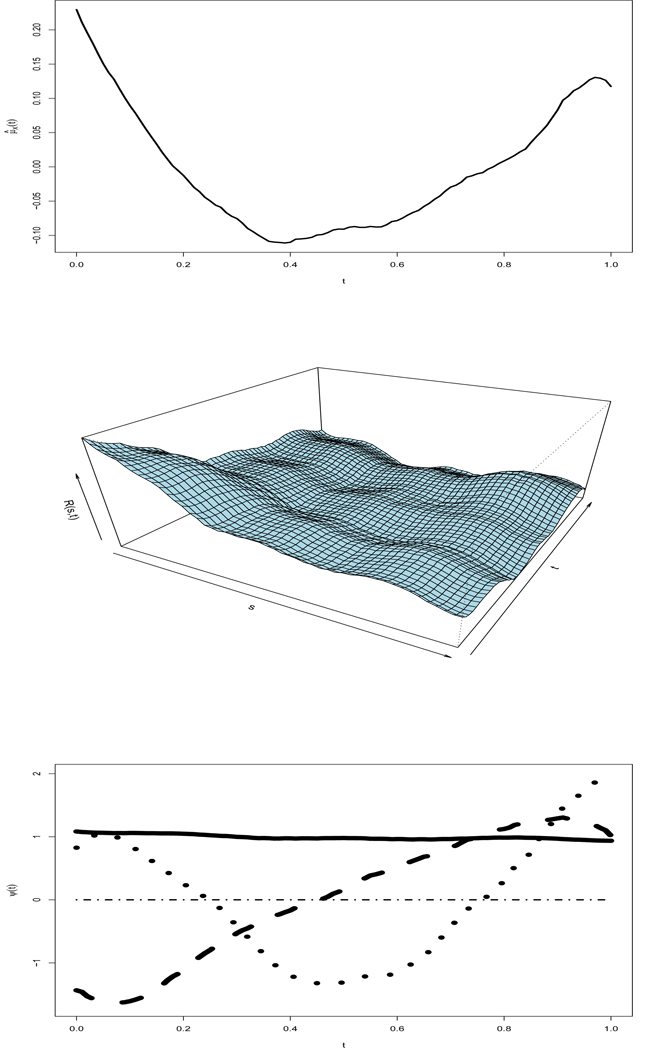
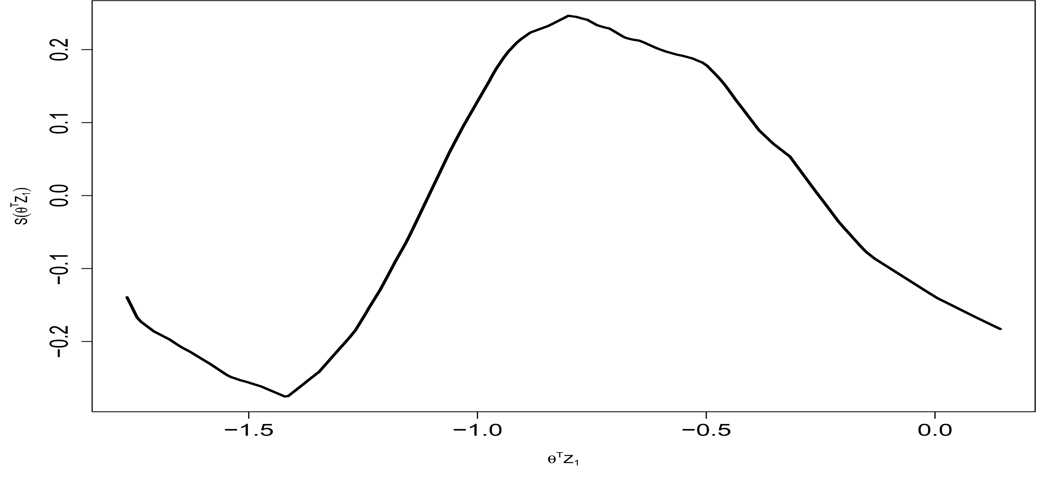
We first performed FPCA on the p27 data. In Figure 1, we show μ̂_X(t), R̂(s, t) and the first 3 estimated PCs. The first 3 eigenvalues are 0.871, 0.019 and 0.005 respectively. The estimated variance for the measurement error is ${\widehat{\sigma }}_{\epsilon }^2=0.103$. We again implemented the AIC criterion to choose the number of significant principal components in the p27 data, and p = 2 was picked. We thus only include the first 2 principal components of the p27 data in the regression model, so that α₁ = (α₁₁, α₁₂)^T and ${\mathit{\alpha }}_2=({\alpha }_{21},{\alpha }_{22}^{\mathrm{T}})$. The estimated parameters are presented in Table 3, and the estimated S(·) is shown in Figure 2.

Figure 1.

Functional principal component analysis for the colon carcinogenesis p27 data. Top panel: local linear estimator of the mean curve μ_X(t); middle panel: local linear estimator of the covariance function; lower panel: the first 3 principal components. The solid curve, the dashed curve and the dotted curve are the first 3 principal components, respectively.

Table 3.

Estimated parameters in the colon carcinogenesis data. The standard errors were estimated by bootstrap, and the p-values are for the null hypothesis that the parameter = 0.0. Here the two principal component values have α₁ = (α₁₁, α₁₂)^T and α₂ = (α₂₁, α₂₂)^T. The subscripts ”fish”, ”buty” and ”prolif” refer to effects of a fish oil diet, butyrate supplementation and mean cell proliferation, respectively.

	α11	α12	α21	α22
Estimate	−0.0004	0.0235	−0.0480	0.9988
SE	0.0108	0.1003	0.1653	0.0767
p-value	0.9719	0.8145	0.7714	0.0000
	β0	βfish	βbuty	βprolif
Estimate	0.2627	0.0514	0.0223	−0.0062
SE	0.0247	0.0193	0.0201	0.0135
p-value	0.0000	0.0078	0.2667	0.6484
	θfish	θbuty	θprolif
Estimate	0.4208	−0.7143	−0.5592
SE	0.2847	0.2419	0.2005
p-value	0.1394	0.0031	0.0053

Figure 2.

Nonparametric estimator of S(·) in the colon carcinogenesis p27 data.

We estimated the standard error of our parameter estimates by a bootstrap procedure. Of course, after resampling the individual curves (crypts) we reran the functional principal component analysis in the bootstrap sample, so that the bootstrap standard error estimator automatically takes into account the estimation error in FPCA. We then refit the model to the new sample. The procedure was repeated 1, 000 times, and the standard deviations of the estimators in the bootstrap samples were used as our standard error estimators. We then tested each parameter in turn to see whether the true parameter is equal to 0.00. The estimated standard errors and the p-values are reported in Table 3.

To summarize, the parameters, β_fish, α₂₂, θ_buty and θ_prolif, have corresponding p-values less than 0.01. For the parametric main effect, the positive significant β_fish implies that the fish oil diet enhances the apoptotic index. The positive β̂_buty and the negative β̂_prolif suggest that the butyrate supplement and the increasing proliferation level are positively and negatively associated with the apoptotic index, respectively, even though neither is significant at the main effect level. The statistically significant results for α₂₂, θ_buty and θ_prolif imply that the second principal component of the p27 process is interacting with butyrate supplementation and proliferation.

5.2.3 Testing for Interactions

In addition to testing if each individual parameter is equal to 0.00, it is important to have an overall test of whether interaction really exists in this data set. In our model, this is equivalent to testing the null hypothesis H₀ : S(·) ≡ 0. We test this null hypothesis using the following parametric bootstrap procedure:

Step 1. Fit the model under the null hypothesis given as $\mathrm{E}(Y_i|{\mathit{\xi }}_i,{\mathit{Z}}_i)={\mathit{\xi }}_i^{\mathrm{T}}{\mathit{\alpha }}_1+{\mathit{Z}}_i^{\mathrm{T}}\mathit{\beta }$. Denote the estimators under the reduced model as α̂_1,red and β̂_red, and call the estimated conditional variance of Y under the reduced model ${\widehat{\sigma }}_{Y,\text{red}}^2$. We assume the data are Gaussian, and calculate the log likelihood ratio of the full model with interaction to the reduced model above.

Step 2. Use the estimated reduced model as the true one to generate bootstrap samples. We resample with replacement n crypts from the original collection. For the i^th resampled crypt, we retain the original covariate vector Z_i, use the estimated principal component score and estimated eigenfunction to regenerate the p27 observations $W_{\mathit{\text{ij}}}^{*}={\widehat{\mu }}_X(t_{\mathit{\text{ij}}})+{\displaystyle {\sum }_{k=1}^K{\widehat{\xi }}_{\mathit{\text{ik}}}{\widehat{\psi }}_k(t_{\mathit{\text{ij}}})+U_{\mathit{\text{ij}}}^{*},\text{where}{U}_{\mathit{\text{ij}}}^{*}=\text{Normal}(0,{\widehat{\sigma }}_u^2),{\widehat{\xi }}_{\mathit{\text{ik}}},{\widehat{\psi }}_k(·)\text{and}}{\widehat{\sigma }}_u^2$ are estimates from the original data. We choose K = 2 to be consistent with our data analysis. Then $Y_i^{*}$ is generated by $Y_i^{*}~\text{Normal}({\widehat{\mathit{\xi }}}_i^{\mathrm{T}}{\widehat{\mathit{\alpha }}}_{1,\text{red}}+{\mathit{Z}}_i^{\mathrm{T}}{\widehat{\mathit{\beta }}}_{\text{red}},{\widehat{\sigma }}_{Y,\text{red}}^2)$.

To apply the estimation procedure to the bootstrap sample, we performed the principal component analysis to the regenerated observations $\{(t_{\mathit{\text{ij}}},W_{\mathit{\text{ij}}}^{*});j=1,\cdots ,m_i,i=1,\cdots ,n\}$, so that our test procedure automatically takes into account the estimation error in FPCA. After FPCA, we apply both the full model and the reduced model to the bootstrap sample and calculate the log likelihood ratio. The bootstrap procedure was repeated 1, 000 times.

Step 3. Compare the log likelihood ratio calculated from the data to the bootstrap quantities, and let the p-value be the upper percentile of the true log likelihood ratio among the bootstrap versions.

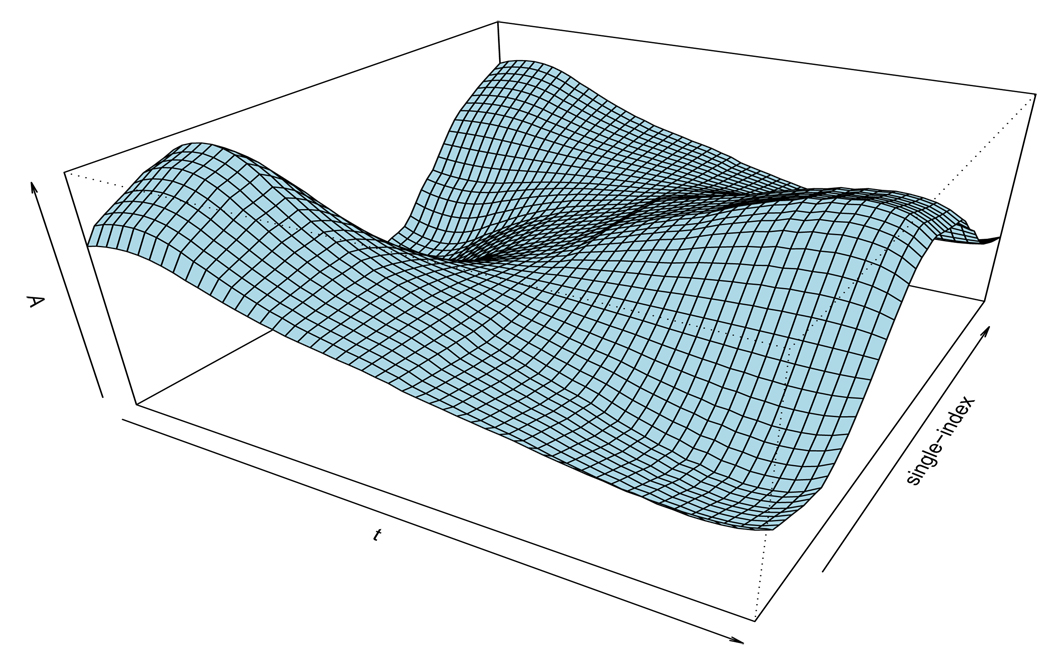
We applied this procedure to the colon carcinogenesis data, and the test yields a p-value of 0.044, which is indication that interaction does exist in these data. To see the effect of this interaction, we also present 𝔄(t, θ^TZ₁) in Figure 3. We can see, as the single-index value θ^TZ₁ changes, the coefficient function for the functional predictor changes quite dramatically. Other inference procedures have been proposed in different semiparametric models. Among them, Liang et al. (2009) proposed an empirical likelihood based inference for generalized partially linear models and Li and Liang (2008) proposed to use a semiparametric generalized likelihood ratio test to select significant variables in the nonparametric component in the generalized varying-coefficient partially linear models. How to adopt their testing ideas in our models warrants future research.

Figure 3.

Semiparametric estimator of 𝔄(t, θ^TZ₁) in the colon carcinogenesis p27 data.

5.2.4 Further Investigation of Interaction

One interesting finding of our study is that when we apply the reduced model without interaction to the data, the only significant parameter is the main effect of diet. In other words, none of butyrate supplementation, proliferation and p27 show strong main effects. These factors only show their effects in the full model that includes an interaction.

To further confirm this conclusion, we also did another simulation. We bootstrapped crypts from the original data, but regenerated Y using our estimated full model with interactions. We then applied the reduced model to the simulated data sets. Again, none of the factors besides the fish oil diet showed significant main effects.

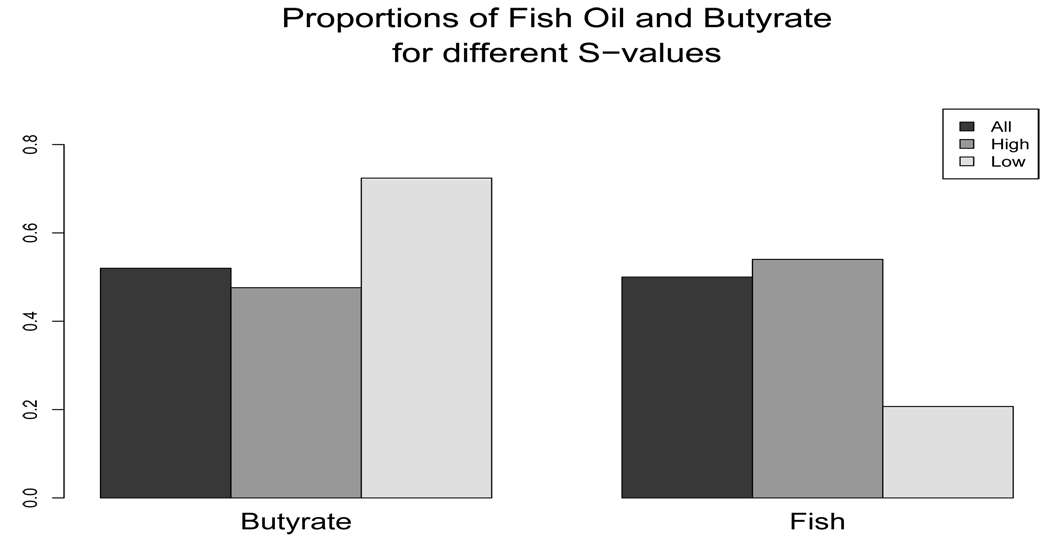
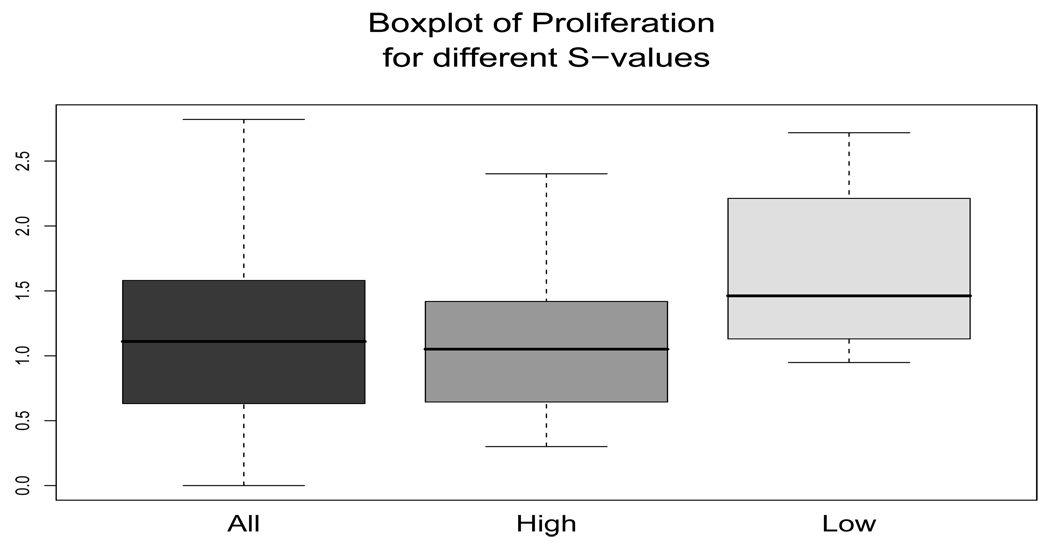
We now further look into the interactions between p27 and other covariates through the PC scores of p27 and S(·) values of the single index θ^TZ₁. To eliminate the influence of potential boundary effects, we focus on data points that are within the internal area of S(·). Precisely, we truncated 10% of the points from either side of the boundary of the range of θ^TZ₁. We then divided the data points into three subgroups: those that give high values of S(·) (S_high: S > 1.5); those ones give low values of S(·) (S_low: S < −1.5); and the ones that are in between (S_mid), where ”high”, ”low”, and ”mid” imply positive, negative and zero values of S. In Figure 4, we plot the proportions of observations for all data values, the data in S_low and the data in S_high that receive fish oil diet and butyrate supplement, respectively. In Figure 5, we plot the three corresponding boxplots of proliferation values. We can see that the proportions of butyrate and fish oil for all data values and for those in S_high are similar, but for the S_low group, the proportion of butyrate supplements is higher while the proportion of fish oil is lower than the others. An equivalent statement applies to the distributions of proliferation. The S_low group tends to have higher proliferation while the proliferation of the S_high group is in general similar to the overall distribution.

Figure 4.

Proportions of crypts receiving butyrate supplementation (left panel) and fish oil (right panel), depending on the levels of S(·). The left bar in each panel refers all crypts, the middle bar to the case that S(·) is high and the right to cases that S(·) is low.

Figure 5.

Boxplots of proliferation depending on values of S(·). Here ”All”, ”High” and ”Low” refer to all observations, those with high values of S(·) and those with low values of S(·).

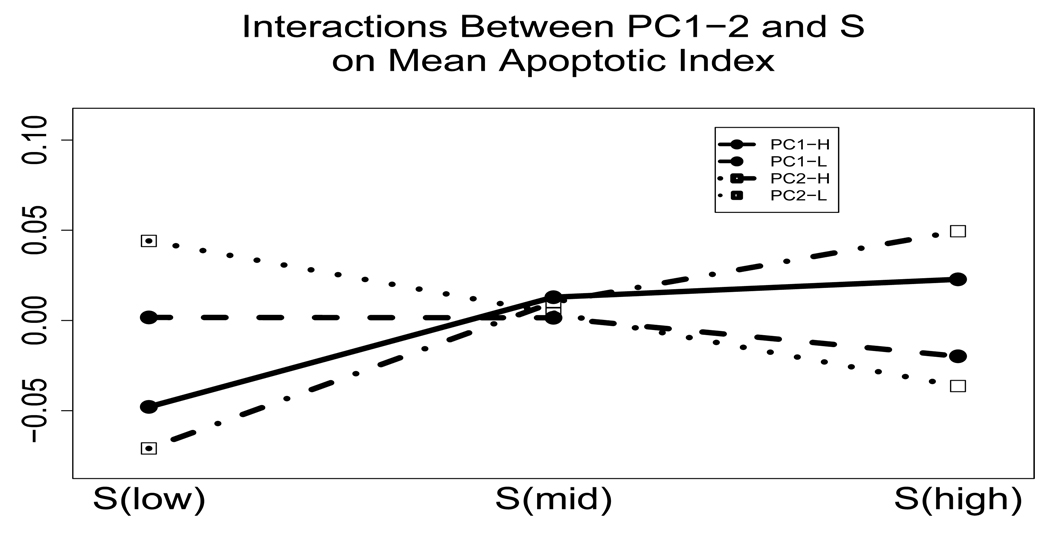
To understand the interacting effects of p27 and θ^TZ₁ on the apoptotic levels through the p27 PC scores, we produce Figure 6. We first removed the estimated main effects by subtracting them from the apoptotic levels and refer to the adjusted values as apoptotic indices. We then dichotomized each of the two p27 PC scores according whether they belong to the top or bottom 50% of the scores; this practice allows us to produce 4 groups for the 2 PC-scores: PC1-Low, PC1-High, PC2-Low and PC2-High. An entry that belongs to PC1-Low tends to have a lower than average p27 and that in PC2-Low tends to have its p27 values lower in the top of the crypts. The equivalent implications apply to the PC1-High and PC2-High groups. We calculated the average apoptotic indices of these four PC groups against S_low, S_mid and S_high and plot them in Figure 6. The solid circle and square indicate the membership of PC1 and PC2, while the solid, dashed, dash-dotted and dotted lines indicate the membership of PC1-High, PC1-Low, PC2-High and PC2-Low, respectively. Figure 6 clearly shows that there are interactions between PC scores of p27 and S(θ^TZ₁). When the p27 average is high (PC1-High) or it is higher on the top (PC2-High) of the crypt, whether there is a reduction of the apoptotic indices seems to be partly determined by whether there is a high proliferation level under butyrate supplementation. When the p27 average is low (PC1-Low), other covariates seem to have little effect on the change of the apoptotic index. On the other hand, if p27 levels are higher on the bottom of the crypt (PC2-Low), the high proliferation level under butyrate supplementation seems to induce an increment of the apoptotic index.

Figure 6.

Interaction between levels of the first two principal components and level of the function S(·). Here ”PC1” and ”PC2” are the first and second principal components, respectively, while subscripts ”Low” and ”High” indicate whether they are below or above the fiftieth percentile. The terms S(low), S(mid) and S(high) refer to low, medium and high values of S(·). The solid line refers to PC1-High, the dashed to PC1-Low, the dash-dotted to PC2-High and the dotted to PC2-Low.

6 Conclusions

We have introduced a new class of functional generalized linear models that includes multivariate covariates and their interaction with the functional predictor. To achieve parsimony, the interaction is modeled semiparametrically with a single-index structure.

When the functional features related to the response variable are known basis functions, we proposed a two step procedure based on local estimation equations. We showed theoretically that the first step of the procedure produces a consistent estimator, while the second step estimator is more efficient and is asymptotically normal with a root n rate.

We further investigated the situation that the functional features are data-driven, i.e. the principal components of the process. We applied the functional principal component analysis of Yao et al. (2005) and Hall et al. (2006) to the discrete observations on the functional data, and plugged the estimated principal component scores into the two step procedure. We showed that when we have a large number of subjects, and enough number of observations on each curve, the initial estimator in our first step procedure is still consistent, while the second step estimator is still root-n consistent and asymptotically normal.

One important finding is that asymptotic variance of our second step estimator is larger than in the case that the functional features ξ are known. This extra variation in the estimator is due to the estimation error of the FPCA.

Our theoretical investigation is innovative since almost all the literature on functional data analysis that we are aware of tends to ignore the estimation error in FPCA. The only exception is perhaps the recent paper by Li, Li, Wang and Wang (2008), where estimation error in FPCA was taken into account, but their model did not include interactions between the functional predictor and other covariates. Our results verify that one should be aware of the extra variability when estimating FPCA scores.

Our methods were illustrated by a simulation study and applied to a colon carcinogenesis data set. In studying this FGLM model, we detected a previously unknown interaction of the response, p27, with the environmental covariates.

Appendix: Asymptotic Covariance Matrices in Theorems 2 and 4

Throughout, η{α, β, θ, S(·)} = η{Θ, S(·)} denotes the expression ${\mathit{\alpha }}_1^{\mathrm{T}}\mathit{\xi }+\mathit{S}({\mathit{\theta }}^{\mathrm{T}}{\mathit{Z}}_1){\mathit{\alpha }}_2^{\mathrm{T}}\mathit{\xi }+{\mathit{\beta }}^{\mathrm{T}}\mathit{Z}$, and the subindices “i” and “ij” of η indicate the replacement of each random variable by the corresponding observations. Provided that the clarity of the presentation is preserved, we also leave out arguments of functions to simplify certain equations.

Define ${\epsilon }_i=q_1\left\{{\eta }_i,Y_i\right\}$,

$$\begin{array}{c}{𝒱}_1(\mathbf{z};\mathit{\theta })=\mathrm{E}\{{\rho }_2({\eta }_i){({\mathit{\alpha }}_{2,0}^{\mathrm{T}}{\mathit{\xi }}_i)}^2|{\mathit{\theta }}^{\mathrm{T}}{\mathit{Z}}_{i1}={\mathit{\theta }}^{\mathrm{T}}\mathbf{z}\},\hfill \\ {\mathit{\pi }}_{i1}={\rho }_2({\eta }_i)({\mathit{\alpha }}_{2,0}^{\mathrm{T}}{\mathit{\xi }}_i)\left\{\begin{array}{c}{\mathit{\xi }}_i\\ \mathit{S}({\mathit{\theta }}_0^{\mathrm{T}}{\mathit{Z}}_{i1}){\mathit{\xi }}_i\\ {\mathit{Z}}_i\end{array}\right\},{\mathit{\pi }}_{i2}={\rho }_2({\eta }_i){({\mathit{\alpha }}_{2,0}^{\mathrm{T}}{\mathit{\xi }}_i)}^2{\mathit{Z}}_{i1},\hfill \\ {\widehat{\mathit{\pi }}}_1(\mathbf{z};\mathit{\theta })=\mathrm{E}({\mathit{\pi }}_{i1}|{\mathit{\theta }}^{\mathrm{T}}{\mathit{Z}}_{i1}={\mathit{\theta }}^{\mathrm{T}}\mathbf{z}),{\widehat{\mathit{\pi }}}_2(\mathbf{z};\mathit{\theta })=\mathrm{E}({\mathit{\pi }}_{i2}|{\mathit{\theta }}^{\mathrm{T}}{\mathit{Z}}_{i1}={\mathit{\theta }}^{\mathrm{T}}\mathbf{z}),\hfill \end{array}$$

and 𝒱₃(z; θ) is a symmetric matrix whose (ℓ₁, ℓ₂)^th block is denoted by ${𝒱}_3^{[{\ell }_1,{\ell }_2]}\text{for}{\ell }_1,{\ell }_2=1,2$, and

$$\begin{array}{c}{𝒱}_3^{[1,1]}(\mathbf{z};\mathit{\theta })=\mathrm{E}[{\rho }_2({\eta }_i){\left\{\mathit{S}\begin{array}{c}{\mathit{\xi }}_i\\ ({\mathit{\theta }}_0^{\mathrm{T}}{\mathit{Z}}_{i1})\\ {\mathit{Z}}_i\end{array}{\mathit{\xi }}_i\right\}}^{\otimes 2}|{\mathit{\theta }}^{\mathrm{T}}{\mathit{Z}}_{i1}={\mathit{\theta }}^{\mathrm{T}}\mathbf{z}],\hfill \\ {𝒱}_3^{[1,2]}(\mathbf{z};\mathit{\theta })={\mathit{S}}^{(1)}({\mathit{\theta }}_0^{\mathrm{T}}\mathbf{z})\{\mathrm{E}({\mathit{\pi }}_{i1}{\mathit{Z}}_{i1}^{\mathrm{T}}|{\mathit{\theta }}^{\mathrm{T}}{\mathit{Z}}_{i1}={\mathit{\theta }}^{\mathrm{T}}\mathbf{z})-{\widehat{\mathit{\pi }}}_1(\mathbf{z};\mathit{\theta }){\mathit{z}}^{\mathrm{T}}\},\hfill \\ {𝒱}_3^{[2,1]}(\mathbf{z};\mathit{\theta })={\{{𝒱}_3^{[1,2]}(\mathbf{z};\mathit{\theta })\}}^{\mathrm{T}},\hfill \\ {𝒱}_3^{[2,2]}(\mathbf{z};\mathit{\theta })={\{{\mathit{S}}^{(1)}({\mathit{\theta }}_0^{\mathrm{T}}\mathbf{z})\}}^2[\mathrm{E}\{{\rho }_2({\eta }_i){({\mathit{\alpha }}_{2,0}^{\mathrm{T}}{\mathit{\xi }}_i)}^2{\mathit{Z}}_{i1}{\mathit{Z}}_{i1}^{\mathrm{T}}|{\mathit{\theta }}^{\mathrm{T}}{\mathit{Z}}_{i1}={\mathit{\theta }}^{\mathrm{T}}\mathbf{z}\}-{\widehat{\mathit{\pi }}}_2(\mathbf{z};\mathit{\theta }){\mathit{z}}^{\mathrm{T}}-\mathbf{z}{\widehat{\mathit{\pi }}}_2^{\mathrm{T}}(\mathbf{z};\mathit{\theta })+{𝒱}_1(\mathbf{z};\mathit{\theta }){\mathbf{\text{zz}}}^{\mathrm{T}}].\hfill \end{array}$$

Let

$${𝒩}_n=n^{-1}{\displaystyle {\sum }_{j=1}^n{\epsilon }_i\left[\begin{array}{c}{\mathit{\xi }}_i-{𝒱}_1^{-1}({\mathit{Z}}_{i1};{\mathit{\theta }}_0)({\mathit{\alpha }}_{2,0}^{\mathrm{T}}{\mathit{\xi }}_i)\mathrm{E}\{{\rho }_2(\eta )({\mathit{\alpha }}_{2,0}^{\mathrm{T}}\mathit{\xi })\mathit{\xi }|{\mathit{\theta }}_0^{\mathrm{T}}{\mathit{Z}}_1={\mathit{\theta }}_0^{\mathrm{T}}{\mathit{Z}}_{i1}\}\\ \mathit{S}({\mathit{\theta }}_0^{\mathrm{T}}{\mathit{Z}}_{i1}){\mathit{\xi }}_i-{𝒱}_1^{-1}({\mathit{Z}}_{i1};{\mathit{\theta }}_0)({\mathit{\alpha }}_{2,0}^{\mathrm{T}}{\mathit{\xi }}_i)\mathrm{E}\{{\rho }_2(\eta )({\mathit{\alpha }}_{2,0}^{\mathrm{T}}\mathit{\xi })\mathit{S}|({\mathit{\theta }}_0^{\mathrm{T}}{\mathit{Z}}_1)\xi |{\mathit{\theta }}_0^{\mathrm{T}}{\mathit{Z}}_1={\mathit{\theta }}_0^{\mathrm{T}}{\mathit{Z}}_{i1}\}\\ {\mathit{Z}}_i-{𝒱}_1^{-1}({\mathit{Z}}_{i1};{\mathit{\theta }}_0)({\mathit{\alpha }}_{2,0}^{\mathrm{T}}{\mathit{\xi }}_i)\mathrm{E}\{{\rho }_2(\eta )({\mathit{\alpha }}_{2,0}^{\mathrm{T}}\mathit{\xi })\mathit{Z}|{\mathit{\theta }}_0^{\mathrm{T}}{\mathit{Z}}_1={\mathit{\theta }}_0^{\mathrm{T}}{\mathit{Z}}_{i1}\}\\ ({\mathit{\alpha }}_{2,0}^{\mathrm{T}}{\mathit{\xi }}_i){\mathit{S}}^{(1)}({\mathit{\theta }}_0^{\mathrm{T}}{\mathit{Z}}_{i1})\{{\mathit{Z}}_{i1}-{𝒱}_1^{-1}({\mathit{Z}}_{i1;{\mathit{\theta }}_0}){\widehat{\mathit{\pi }}}_2({\mathit{Z}}_{i1};{\mathit{\theta }}_0)\}\end{array}\right],}$$

and ${𝒩}_{1,n}=n^{-1}{\displaystyle {\sum }_{i=1}^n{\epsilon }_i({\widehat{\mathit{\xi }}}_i-{\mathit{\xi }}_i)}$ where

$$\begin{array}{cc}& {\epsilon }_i=\left[\begin{array}{c}{\mathit{\xi }}_i-{𝒱}_1^{-1}({\mathit{Z}}_{i1};{\mathit{\theta }}_0)({\mathit{\alpha }}_{2,0}^{\mathrm{T}}{\mathit{\xi }}_i)\mathrm{E}\{{\rho }_2(\eta )({\mathit{\alpha }}_{2,0}^{\mathrm{T}}\mathit{\xi })\mathit{\xi }|{\mathit{\theta }}_0^{\mathrm{T}}{\mathit{Z}}_1={\mathit{\theta }}_0^{\mathrm{T}}{\mathit{Z}}_{i1}\}\\ \mathit{S}({\mathit{\theta }}_0^{\mathrm{T}}{\mathit{Z}}_{i1}){\mathit{\xi }}_i-{𝒱}_1^{-1}({\mathit{Z}}_{i1};{\mathit{\theta }}_0)({\mathit{\alpha }}_{2,0}^{\mathrm{T}}{\mathit{\xi }}_i)\mathrm{E}\{{\rho }_2(\eta )({\mathit{\alpha }}_{2,0}^{\mathrm{T}}\mathit{\xi })\mathit{S}({\mathit{\theta }}_0^{\mathrm{T}}{\mathit{Z}}_1)\mathit{\xi }|{\mathit{\theta }}_0^{\mathrm{T}}{\mathit{Z}}_1={\mathit{\theta }}_0^{\mathrm{T}}{\mathit{Z}}_{i1}\}\\ {\mathit{Z}}_i-{𝒱}_1^{-1}(Z_{i1};{\mathit{\theta }}_0)({\mathit{\alpha }}_{2,0}^{\mathrm{T}}{\mathit{\xi }}_i)\mathrm{E}\{{\rho }_2(\eta )({\mathit{\alpha }}_{2,0}^{\mathrm{T}}\mathit{\xi })\mathit{Z}|{\mathit{\theta }}_0^{\mathrm{T}}{\mathit{Z}}_1={\mathit{\theta }}_0^{\mathrm{T}}{\mathit{Z}}_{i1}\}\\ ({\mathit{\alpha }}_{2,0}^{\mathrm{T}}{\mathit{\xi }}_i){\mathit{S}}^{(1)}({\mathit{\theta }}_0^{\mathrm{T}}{\mathit{Z}}_{i1})\{{\mathit{Z}}_{i1}-{𝒱}_1^{-1}({\mathit{Z}}_{i1;{\mathit{\theta }}_0}){\widehat{\mathbf{\pi }}}_2({\mathit{Z}}_{i1},{\mathit{\theta }}_0)\}\end{array}\right]\\ & \times q_2({\eta }_i,Y_i){\{{\mathit{\alpha }}_{1,0}+{\mathit{S}}_0({\mathit{\theta }}_0^{\mathrm{T}}{\mathit{Z}}_{i1}){\mathit{\alpha }}_{2,0}\}}^{\mathrm{T}}.\hfill \end{array}$$

Finally, define 𝒜, ℬ and B₁ in Theorems 2 and 4 as:

$$𝒜=\mathrm{E}\{{𝒱}_3({\mathit{Z}}_1;{\mathit{\theta }}_0)\},ℬ=n\times \text{cov}({𝒩}_n),{ℬ}_1=\underset{n\to \infty }{\text{lim}}n\times \text{cov}({𝒩}_{1,n}).$$