An Analytical Model for Genetic Hitchhiking in the Evolution of Antimalarial Drug Resistance

Abstract

We analytically study a deterministic model for the spread of drug resistance among human malaria parasites. The model incorporates all major characteristics of the complex malaria-transmission cycle and accounts for the fact that only a fraction α of infected hosts receive drug treatment. Furthermore, the model incorporates that hosts can be co-infected. The number m of parasites co-infecting a host is either a constant or, more generally, follows a given frequency distribution.

Although the model is formulated in a multilocus setup, for our results we assume that drug resistance is caused by a single locus with two alleles - a sensitive one and a resistant one. We assume that the resistant allele has a selective advantage only in treated hosts and pays metabolic costs, which causes this allele to be deleterious in untreated hosts. We provide necessary and sufficient conditions for the fixation of the resistant allele. Moreover, provided the resistant allele will sweep through the population, we derive a formula for the time until it reaches a given frequency and in particular for the time until quasi-fixation.

Furthermore, we establish an analytical solution for allele frequency changes at a linked neutral biallelic locus due to the rapid increase in frequency of the resistant allele. Our solution describes a local reduction in heterozygosity among parasite chromosomes around the resistant allele, the effect commonly referred to as the hitchhiking effect, as a function of α and m. The result therefore allows the investigation of selective sweep patterns under specific demographic settings. We find that the hitchhiking effect is similar but different from the standard model of genetic hitchhiking that assumes random mating and homogeneous selection. In particular, the process of recombination and selection cannot be decoupled. We further explain why standard hitchhiking theory cannot be applied to drug resistance in malaria. Furthermore, we will show that a genome-wide reduction in relative heterozygosity can occur provided a fraction of hosts is infected by a single parasite haplotype.

Finally, we show how to incorporate host heterogeneity, and generalize our results to this bio logically more realistic case.

1 Introduction

Malaria is still a threat to the public health in large areas of the developing world. It is an infectious disease produced by protozoan parasites of the genus Plasmodium, with Plasmodium falciparium, being responsible for the most virulent form of human malaria (Snow et al., 2005; Laxminarayan, 2004). P. falciparum causes high morbidity and mortality which annually results in 200 million to 300 million infections and one to three million deaths (cf. WHO, 2000). Malaria control is highly dependent on drug treatments that kill parasites in infected hosts. Chloroquine (CQ) was used as an effective antimalarial drug for decades. However, the emergence and spread of CQ resistance rendered it useless for treating P. falciparum malaria in many endemic areas (Wellems and Plowe, 2001). Subsequently, a combination therapy using sulfadoxine and pyrimethamine (SP) replaced CQ as a widely used treatment. Unfortunately, resistance to SP also evolved in several geographic areas and continues to spread in sub-Saharan Africa (Gregson and Plowe, 2005). Currently, artemisinin-based combination therapies (ACTs) are adopted as the next line of treatment (White, 2004). However, there are concerns that resistance against these drugs will also evolve (Duffy and Sibley, 2005).

Malaria parasites undergo a complex transmission cycle with sexual phases in the mosquito vector and asexual phases in the infected host (Daily, 2006). A human host is inoculated with sporozoites by the bite of an infected Anopheles mosquito during its blood meal. In the human host the sporozoites migrate first to the liver where they differentiate into hepatic merozoites. These are released into the blood stream where some of the hepatic merozoites form gametocytes. The haploid gametocytes are extracted by a mosquito during its blood meal, immediately reproduce sexually in the mosquito’s gut and consequently undergo recombination. Completing the transmission cycle, this step is followed by the production of haploid sporozoites in the mosquitos’s salivary glands from which they can be inoculated into a human host (see Figure 1 for an illustration of the transmission cycle).

Figure 1.

Illustration of the transmission cycle.

The limited repertoire of safe, effective, and affordable antimalarial drugs has made research on the emergence and dispersion of resistance a global health priority. Mathematical models that can use input from genetic data to investigate the dynamic of mutations associated with drug resistance are urgently needed for designing drug-deployment policies that can increase the lifespan of the available drugs. This requires a detailed understanding of population genetic processes that lead to the emergence and dispersion of drug resistance. Unfortunately, the highly complex nature of the malaria-transmission cycle as well as complex demographic and environmental factors aggravate the efforts to elaborate theoretical models. Another source of complication is that many environmental and clinical factors differ tremendously across the worldwide distribution of this parasite. The transmission rate and hence the number of secondary infections varies from very low rates in parts of South America, over intermediate rates in Southeast Asia, to high rates in Africa. On the other hand the level of host-acquired immunity is much higher (which means a high number of asymptomatic infections) in most of the affected areas in Africa than in other parts of the world. Such variation in the host-acquired immunity affects drug use.

Among others, two important variables that summarize the demographic and clinical setting of the particular geographic area are the (average) number of parasites (m) co-infecting a given host (the average multiplicity of infection), which is determined by transmission intensity, and the proportion (α) of infected hosts that are drug treated, which mainly depends on how many hosts acquired immunity.

Several studies built population-genetic models that demonstrated profound effects of m and α on the rate of drug-resistance evolution (Hastings and Mackinnon, 1998; Mackinnon and Hastings, 1998; Hastings, 2003, 2006). However, it is still not clear which mechanisms are important to the spread of resistance, i.e., intra-host dynamics, drug half life, multiple drug treatment, migration, multiple infections, recombination, mutation etc.

While it is difficult to build a mathematical model to predict the dynamics of drug resistance that considers this level of complexity involving several factors, we may understand how these factors affect the dynamics by analyzing the empirical patterns of drug-resistance evolution that occurred in several geographic areas with different transmission intensity and drug usage. This analysis is possible only if we can reconstruct the past dynamics of drug resistance in a given population. In the absence of reliable public-health records, such retrospective analysis may not be feasible. However, fast accumulation of parasite genome-sequence data provides a means to indirectly examine the past events of drug resistance evolution without epidemiological data: by examining “selective sweeps” around the loci of drug resistant mutations, one may obtain basic information about the dynamics of resistant mutations.

A selective sweep, or the “hitchhiking” effect of an advantageous mutation, refers to the elimination of pre-existing genetic variation when a particular chromosome segment carrying a favored allele sweeps through the population (Maynard Smith and Haigh, 1974; Stephan et al., 1992; Barton, 2000). The extent of this wipe-out depends on how fast the favored allele increases to high frequency while meiotic recombination is constantly eroding the association between the favored allele and the surrounding chromosome segment (Kim and Stephan, 2002). The chromosomal span of reduced variation thus depends on the relative reproductive advantage of resistant alleles over sensitive alleles, which determines the speed of frequency increase. Therefore, by measuring the span of selective sweeps, we may infer the selective pressures on drug resistance and relate it to the demographic and clinical factors specific to the population under examination.

In malaria biology, detection of selective sweeps mainly contributed to confirming the location of drug resistant mutations and elucidating their mutational origins (Wootton et al., 2002; Nash et al., 2005; Mita et al., 2007; Nair et al., 2007; McCollum et al., 2008), while fewer studies attempted to relate the span of selective sweeps with the strength of drug selection. Nair et al. (2003) for example observed a severe reduction of variation at microsatellite loci spanning over 100 kb region surrounding dhfr gene, which was found to mutate to confer resistance to pyrimethamine, in a Southeast Asian population of P. falciparum and examined whether this is compatible with the strength of drug selection inferred by the rate of increase in drug resistance over several years. Using known recombination rates and the result of standard model of selective sweeps, it was concluded that the observed pattern of selective sweep is compatible with the prediction. However, application of the standard selective-sweep model, in which an advantageous allele under constant selective pressure spreads in a random-mating population, to a malaria-parasite population is highly problematic. As we will demonstrate below in detail, the unique mating structure and selective environment of malaria parasites make it impossible to decouple the process of selection and recombination. More importantly, the standard hitchhiking model does not allow to investigate how demographic factors, such as m and α, influence the pattern of selective sweeps.

We shall point out two main differences to standard hitchhiking theory inherent in the malaria transmission cycle. First, parasites are exposed to different selection pressures in treated and untreated host. Second, recombination is restricted, because it occurs immediately after the mosquito takes its blood meal. Hence, recombination occurs exclusively between genetic material originating from the same host. (However, a host can acquire haplotypes from different mosquitos, which will be incorporated in our model.) This fact will lead to an increased rate of selfing and consequently restrict recombination. In the most extreme case a host carries only one haplotype, such that only selfing, and hence no recombination, occurs when it is taken by a mosquito. The role of selfing was already emphasized by Mackinnon and Hastings (1998) and Nair et al. (2003). However, they use only a heuristic formula that corrects for the effect of selfing. Another limitation of their approach is the fact that it is numerical. Here, we will overcome both of this weaknesses by first deriving exact equations incorporating selfing and by establishing analytical results.

In this article we introduce a model of drug-resistance evolution and the associated selective-sweep pattern that is simple enough to be analyzed analytically but sufficiently complex to cover the basic mechanisms of the malaria transmission cycle. More precisely, we deterministically model the spread of an allele causing drug resistance in a large population of infected hosts in which a fixed proportion undergoes drug treatment.

We first derive exact conditions for the spread of such an allele under flexible assumptions of drug efficiency including reproductive costs of resistance. The main focus of this article is to predict the hitchhiking effect of a resistant mutation sweeping through the parasite population under drug pressure. We derive the equilibrium allele frequencies at linked neutral loci and the average heterozygosity following the classical pathway of Maynard Smith and Haigh (1974), but under the malaria transmission cycle and division into treated and untreated hosts. Our results are a useful first step to compare the analytical predictions of the hitchhiking effect with real data to infer the selection parameters in real populations. Having examined realistic selection parameters, i.e., drug-efficiency parameters and metabolic costs of mutations causing resistance, our results permit us to quantify the effect of the proportion of treated hosts on the time of the spread of drug resistance. This may in turn allow inferences on future drug-treatment policies.

2 Overview of the model

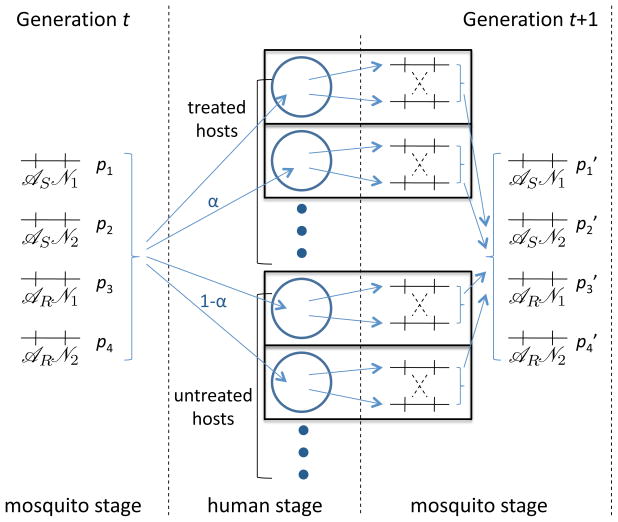
To effectively analyze the evolution of antimalarial drug resistance, we use a model of a malaria parasite population whose reproductive structure is simplified in a manner similar to that in Mackinnon and Hastings (1998). We assume that parasites reproduce in discrete generations, where a ‘generation’ corresponds to one transmission cycle depicted in Figure 1. In each generation, parasites simultaneously proceed through two non-overlapping stages. The “human stage” is when parasites reproduce asexually inside hosts before being transmitted to mosquitoes. The “mosquito stage” refers to when parasites reproduce sexually inside mosquitoes and are ready to be transferred to human hosts. This leads to the simplified model illustrated in Figure 2.

Figure 2.

Illustration of the model structure. Hosts acquire infections by multinomially sampling m sporozoites from the parasite population according to their distribution in generation t. Selection occurs in the host population. Parasites are selected independently in each host. Gametocytes are taken by the mosquitos during their blood meals, and recombination occurs only between gametocytes originating from the same host (only gametocytes further participate in the transmission cycle). After recombination the parasite population is pooled together yielding the frequency distribution of sporozoites in generation t + 1.

Assume L multi-allelic loci in a genome of haploid parasites, and let n_i be the number of alleles segregating at locus i. Hence, the number of haplotypes is $n={\displaystyle \prod _{i=1}^L}{n}_i$. We number the n haplotypes by 1, …, n in the usual order. We assume that the size of the parasite population is very large such that the evolutionary changes occur deterministically. Let p₁, …, p_n denote the relative frequencies of the parasite haplotypes in the mosquito stage, and p = (p₁, …, p_n) the vector of haplotype frequencies. There is an (infinitely) large number of hosts. We assume that each host is infected randomly and independently by exactly m parasites. (We assume m to be a fixed parameter until Section 6, where we assume that m follows a fixed frequency-distribution.)

Hosts acquire parasite strains according to their frequencies in the mosquito stage. Hence, the configuration of infections in hosts is multinomially distributed with parameters m and p₁, …, p_n. We assume that independently-infecting parasite clones are found in equal frequencies in a host. Hence, the relative frequency of a haploid clone in a host before selection is $\frac{1}{m}$. Let us denote a multi-index by m = (m₁, …, m_n), and the sum over its components by $\mid \mathit{m}\mid ={\displaystyle \sum _{i=1}^n}{m}_i$. The probability that a host is infected by m_i copies of haplotype i (i = 1, …, n, |m| = m) is given by $\left(\begin{array}{c}m\\ \mathit{m}\end{array}\right){\mathit{p}}^{\mathit{m}}$, where $\left(\begin{array}{c}m\\ \mathit{m}\end{array}\right)=\frac{m!}{{\displaystyle \prod _{i=1}^n}{m}_i!}$ denotes the respective multinomial coefficient and, as usual, ${\mathit{p}}^{\mathit{m}}:={\displaystyle \prod _{i=1}^n}{p}_i^{m_i}$.

After a host is infected the parasites reproduce clonally in the host. We assume that a fixed proportion α of infected hosts in the population is treated, whereas the remaining hosts are untreated. The rate of reproduction of the haplotypes is different in treated and untreated hosts. The absolute fitness of a parasite strain is the expected number of its descendants in the host at the time of the mosquito’s blood meal. The absolute frequency of haplotype i in an untreated host before a mosquito takes its blood meal is denoted by $\frac{m_i}{m}{W}_i^{(U)}$, whereas the absolute frequency of haplotype i in a treated host before a mosquito takes its blood meal is denoted by $\frac{m_i}{m}{W}_i^{(T)}$. (In the following, wherever it is appropriate, we use the superscript (.) to subsume the superscripts (U) and (T).) Some of these parasites form gametocytes in male or female expression. The frequencies of those are assumed to be proportional to the number of respective haplotypes. Furthermore, we impose that male and female gametocytes occur at the same frequencies. We assume that the number of different gametocytes taken by a mosquito during its blood meal from an infected host is proportional to its frequency in the host. Let γ denote the proportionality constant, which is assumed to be the same for each mosquito. Hence, if the absolute frequencies of parasites in an infected host are $\frac{m_1}{m}{W}_1^{(.)},\dots ,\frac{m_n}{m}{W}_n^{(.)}$, the absolute frequencies of gametocytes absorbed during the blood meal are $\gamma \frac{m_1}{m}{W}_1^{(.)},\dots ,\gamma \frac{m_n}{m}{W}_n^{(.)}$ (only gametocytes further participate in the transmission cycle). Note that this takes drug efficiency into account, because a mosquito will absorb a smaller number of parasites from a host in which drugs efficiently eliminated parasites. Our modeling corresponds to the intra-host dynamics in the model of ‘specific immunity’ (Hastings, 1997) in which the reproductive success of each clone is independent of the presence of other clones in the host as there is no intra-host competition between clones (the implication of this assumption on genetic hitchhiking will be discussed later).

In the mosquitos’ guts recombination occurs immediately after the blood meals during the phase in which meiosis occurs. Mating and meiotic recombination occur only between two gametocytes that exit from the same host. In the gut of a mosquito, which has taken its blood meal from a host initially infected with m_i haplotypes i (i = 1, …, n), the probability that a male k-gametocyte fertilizes a female l-gametocyte is

$$\frac{\gamma \frac{m_k}{m}{W}_k^{(.)}}{\frac{\gamma }{m}{W}_{\mathit{m}}^{(.)}}·\frac{\gamma \frac{m_l}{m}{W}_l^{(.)}}{\frac{\gamma }{m}{W}_{\mathit{m}}^{(.)}}=\frac{m_k{W}_k^{(.)}{m}_l{W}_l^{(.)}}{W_{\mathit{m}}^{{(.)}^2}},$$

where

$$\frac{\gamma }{m}{W}_{\mathit{m}}^{(.)}=\frac{\gamma }{m}\sum _{k=1}^n{m}_k{W}_k^{(.)}$$

is the frequency of gametocytes in the mosquito’s gut. The above probability is the relative frequency of a male k-gametocyte times that of a female l-gametocyte. Therefore, the absolute frequency of pairings of a male k-gametocyte and a female l-gametocyte is the probability of such a fertilization times the absolute numbers of parasites in the gut, i.e.,

$$\frac{\gamma m_k{W}_k^{(.)}{m}_l{W}_l^{(.)}}{{mW}_{\mathit{m}}^{(.)}}.$$ (1)

The probability that a fertilization of a male k-gametocyte to a female l-gametocyte produces a haplotype i is denoted by R(kl → i). Therefore, the absolute frequencies of haplotype i in the population of mosquitos that have taken their blood meal from treated and untreated hosts are respectively

$$p_i^{\ast (.)}=\sum _{\mid \mathit{m}\mid =m}\left(\begin{array}{c}m\\ \mathit{m}\end{array}\right){\mathit{p}}^{\mathit{m}}\sum _{k,l=1}^n\frac{\gamma m_k{W}_k^{(.)}{m}_l{W}_l^{(.)}}{{mW}_m^{(.)}}R(kl\to i),$$

where the sum runs over all multi-indices $\mathit{m}\in {\mathbb{N}}_{+}^n$ with |m| = m. Therefore, the relative haplotype frequencies in the mosquito population become

$$p_i^{\prime }=\frac{\alpha p_i^{{\ast }^{(T)}}+(1-\alpha )p_i^{\ast (U)}}{\alpha {\displaystyle \sum _{k=1}^n}{p}_k^{\ast (T)}+(1-\alpha ){\displaystyle \sum _{k=1}^n}{p}_k^{\ast (U)}}=\frac{p_i^{\ast }}{{\displaystyle \sum _{k=1}^n}{p}_k^{\ast }},$$ (2a)

where

$$p_i^{\ast }:=\alpha p_i^{\ast (T)}+(1-\alpha )p_i^{\ast (U)}.$$ (2b)

Our model might superficially remind the reader of the hard-selection Levene model of migration (cf. Nagylaki, 1992, chapter 6.3), in which treated and untreated hosts correspond to two patches. However, there are two important differences. First, mating in the Levene model occurs randomly among the whole population. In our model mating occurs only between parasites that exited the same host. Second, in our model patches would correspond to treated and untreated hosts that are infected by the same configuration of parasite haplotypes. Hence, ‘patches’ are multinomially distributed among treated and untreated hosts, where the distribution changes between consecutive generations. This would correspond to migration rates which are changing over time.

3 Fixation of an allele causing resistance

Assume only one locus causes resistance, whereas all other loci are selectively neutral. Further assume just two alleles at this locus, the sensitive allele 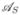, and the resistant allele 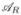. Let us denote the frequency of the resistant allele by p and that of the sensitive allele by 1 − p. The fitnesses of a haplotype carrying the resistant allele in treated and untreated hosts are $w_R^{(T)}$ and $w_R^{(U)}$, respectively, whereas those of the sensitive allele are $w_S^{(T)}$ and $w_S^{(U)}$, respectively. By marginalization of the above dynamics it is straightforward to derive the dynamics for p. This is done in Appendix A.1. By denoting the initial frequency of the resistant allele by p₀ we show that its frequrncy in generation t is given by

$$p(t)=\frac{p_0{\lambda }^t}{p_0{\lambda }^t+(1-p_0){\mu }^t},$$ (3)

where

$$\lambda =\alpha w_R^{(T)}+(1-\alpha )w_R^{(U)}$$ (4a)

is the average fitness of the resistant allele among treated and untreated hosts and

$$\mu =\alpha w_S^{(T)}+(1-\alpha )w_S^{(U)}$$ (4b)

is the average fitness of the sensitive allele among treated and untreated hosts. Thus, we have p(t + 1) > p(t) if and only if α > μ.

Note that the dynamics (3) are intuitive. In the one-locus case our model reduces to the haploid version of the hard-selection Levene model. This is equivalent to the standard haploid one-locus selection model, in which the fitnesses λ and μ are the averages over the respective fitnesses over the two patches (treated and untreated hosts). We summarize

Result 1

The frequency of the resistant allele in generation t is given by (3). The resistant will become fixed in the population if and only if λ > μ.

The dynamics of the resistant allele is independent of the number of parasites infecting a host, i.e., the parameter m. Since m reflects the number of parasites co-infecting a host, the spread of resistance is independent of the number of co-infections.

Since our model assumes that the parasite population is sufficiently (infinitely) large and it is sufficient to track the relative allele frequencies, we can normalize fitnesses and deal with relative rather than with absolute fitnesses. Notably, our model still captures effectiveness of drugs. For our purpose it is convenient to parameterize the fitnesses as

$$\frac{w_R^{(U)}}{1-s}\frac{w_S^{(U)}}{1}\frac{w_R^{(T)}}{1-d_R}\frac{w_S^{(T)}}{1-d_S}.$$ (5)

Hence, the fitnesses are normalized such that the fitness of the sensitive allele in untreated hosts is one. The parameter s corresponds to the fitness disadvantage of the resistant allele due to metabolic costs. Moreover, d_S corresponds to the effect of drug treatment on the fitness of the sensitive allele. The parameter d_R corresponds to the sum of metabolic costs and the effect of drug treatment on the fitness of the resistant allele. A natural assumption is d_S > d_R, i.e., that the sensitive alleles have lower fitness in treated hosts than resistant alleles. An intuitive assumption is d_R ≥ s, i.e., that the fitness of resistant alleles in treated hosts is at least reduced by the amount due to metabolic costs. Note, that d_R = s implies full resistance, i.e., that the fitness of resistant alleles is not affected by drug treatment. Note that asymptomatic infections are usually untreated and parasites are cleared out by the immune system of the host, for instance because of host-acquires or natural immunity. Hence, if these factors are relevant in a particular endemic region, it it can be meaningful to assume d_R < s.

With this new parametrization we can rewrite the fixation condition for the resistant allele as follows.

Remark 1

With the fitnesses parameterized as in (5) the resistant allele will become fixed if and only if

$$\alpha >\frac{s}{d_S-d_R+s}.$$ (6)

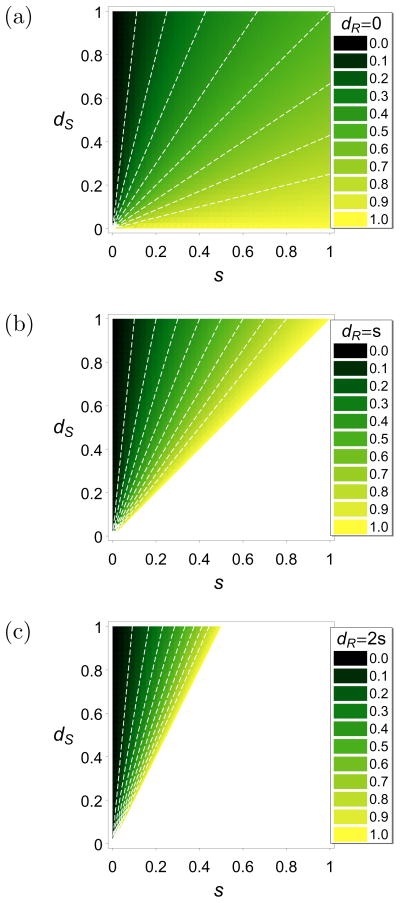
This condition is illustrated in Figure 3 for three different scenarios. In Figure 3(a) it is assumed that the resistant allele is not only fully resistant but also pays no metabolic costs in treated hosts, i.e., d_R = 0. Alternatively, this can be interpreted as a situation in which parasites in untreated hosts participate less in the transmission cycle because they are cleared out because of host-acquired immunity. Figure 3(b) assumes full resistance, i.e., d_R = s, whereas in Figure 3(c) the fitness of resistant alleles is reduced by the same amount as the metabolic costs due to drug treatment, i.e., d_R = 2s.

Figure 3.

Density plots for the threshold value for α. If α is beyond this value the resistant allele will become fixed. The fitnesses are parameterized as in (5). In the white regions the resistant allele is deleterious and gets lost for all values of α. The parameter d_R is specified in the plot legends. The color code is shown in the panels. The white, dashed contour lines are at 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, and 0.9, respectively.

3.1 Time to quasi-fixation

So far we have derived the condition for the resistant allele to sweep through the population. However, as a result of our deterministic approach fixation does not occur within finitely many generations. In reality fixation occurs of course within finite time because of stochastic fluctuations. This will occur readily if the frequency of the resistant allele is sufficiently high. Therefore, we shall emphasize the concept of quasi-fixation (see Kimura (1955)) here, because in the deterministic setup the resistant allele will exceed any frequency less than one within finitely many generations.

The following result follows immediately from (3).

Result 2

Assume the resistant allele occurs initially at frequency p₀ and it will ultimately become fixed, i.e., λ > μ. Its frequency will exceed a given frequency β (0 < β < 1) after generation t ≥ t₀, where

$$t_0:=\frac{log(1-p_0)\beta -log{p}_0(1-\beta )}{log\lambda -log\mu }.$$ (7)

In other words, we have p(t) ≥ β if and only if t ≥ t₀.

Hence, the above result yields the time to quasi-fixation if we choose β sufficiently large. A typical choice is β = 1 − p₀, where the initial frequency p₀ is assumed to be close to zero. Result 2 also shows explicitly how the various parameters affect the time until a given level of resistance is reached, which is important for future public-health policies. Especially, it informs us how the percentage of treated infections and the efficiency of the drug, reflected by the parameters d_R and d_S, affect the time until a given level of resistance is reached. Moreover, the result helps us to evaluate which parameters ranges seem to be biologically reasonable based on our knowledge of drug efficiency, public-health policies, and times for the spread of resistance.

We want to illustrate Result 2 with the following examples.

Example 1

For fixed s the fixation condition (6) for α depends only on the difference d_R − d_S but not on the absolute values of d_R and d_S. However, the time until a given level of resistance is reached depends strongly on the absolute values of d_R and d_S.

Figure 4 shows a density plot of the time at which the resistant allele reaches a frequency of 20% as a function of d_R and d_S for given α, s, and p₀. It is easily seen that this time depends on the absolute values of d_R and d_S, although the condition of fixation depends only on the difference of d_R and d_S. In particular, it decreases if d_R and d_S are increasing while their difference is kept constant.

Figure 4.

Density plot of the time until the resistant allele has reached a frequency β as a function of d_R and d_S, which are according to (5). The parameters are specified in the plot label. The color code is shown on the right in numbers of generations. In the white region the resistant allele cannot be maintained in the population. The white, dashed contour lines are at t = 10, 20, 30, 40, 50, 100, 200, 300, 400 and 500 generations, respectively. The black line corresponds to d_S − d_R = 0.2. It is seen that the time to reach frequency β decreases along the black line if d_R and d_S increase.

Finally we want to provide a more applied example.

Example 2

The parameters $w_R^{(T)}$ and $w_S^{(T)}$ reflect the efficiency of the administered drug, which, for a given drug, reflects the drug dosage at the time of parasite growth. The resistant and sensitive alleles should respond differently to different drug dosages.

Assume that the fitnesses of the resistant and sensitive allele are functions of the administered drug concentration x. Assume they are given by

$$w_S^{(T)}(x)=e^{-C_{S}x}$$ (8a)

and

$$w_R^{(T)}(x)=(1-s)e^{-C_{R}x},$$ (8b)

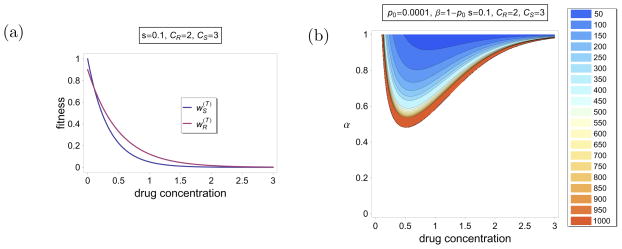
where C_S > C_R > 0. If x = 0, a host is untreated and hence we have $w_S^{(U)}:=w_S^{(T)}(0)$ and $w_R^{(U)}:=w_R^{(T)}(0)$. According to the interpretation of our model, (8) implies that the number of parasites in a human host decline exponentially as the drug concentration is increased. Moreover, the number of sensitive alleles decline quicker than that of the resistant ones. Furthermore, the resistant allele is exposed to metabolic costs reflected by the parameter s. An illustration of this fitnesses if given in Figure 5(a). For a given proportion α of treated hosts, a given initial frequency of the resistant allele, and given parameters s, C_S and C_R, the conditions for fixation of the resistant allele, and the time to quasi-fixation depends crucially on the drug concentration x. This is illustrated in Figure 5(b). Because of the choice of (8), the resistant allele can only sweep through the population if the drug concentration is intermediately high (for given α). If the drug concentration is sufficiently low, the resistant allele is disadvantageous because of its metabolic costs. If the drug concentration is sufficiently high, both the resistant and the sensitive alleles are almost wiped out in treated hosts. Hence, evolution is governed by selection in untreated hosts, in which the resistant allele is disadvantageous. Furthermore, the time to quasi-fixation is shorter for intermediate levels of drug concentration as can be seen from the contour lines in Figure 5(b).

Figure 5.

Illustration of Example 2. (a) Fitnesses of the resistant and sensitive alleles as functions of the drug concentration give by (8). The parameters are specified in the label panel. (b) Contour plot of the time to quasi-fixation. The color code is shown on the right in numbers of generations. In the white region the resistant allele cannot be maintained in the population. The parameters are specified in the label panel. The fintesses are as in (a).

4 Two-locus model

Now, we want to study the hitchhiking effect of the spread of a resistant allele at a single locus on neutral variation. For this purpose we consider two biallelic loci. The first locus is subject to selection with a sensitive allele and a resistant allele segregating. As before 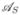and 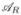denote the sensitive and resistant alleles, respectively. The second locus is selectively neutral with the alleles 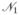and 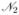segregating. By properly numbering the four resulting haplotypes and parameterizing the fitnesses according to (5) we arrive at the notation summarized in Table 1. Moreover, we denote the recombination rate between the two loci by r.

Table 1.

Summary of notation.

haplotypes
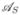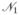
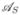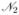
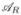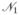
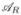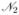
frequency	p1	p2	p3	p4
fitness in untreated hosts	$W_1^{(U)}$	$W_2^{(U)}$	$W_3^{(U)}$	$W_4^{(U)}$
	1	1	1 − s	1 − s
fitness in treated hosts	$W_1^{(T)}$	$W_2^{(T)}$	$W_3^{(T)}$	$W_4^{(T)}$
	1 − dS	1 − dS	1 − dR	1 − dR
sensitive/resistant	sen.	sen.	res.	res.

The tables shows the notation of the four haplotypes, their frequencies, fitnesses in treated and untreated hosts, the respective parametrization of fitness adjusted to (5), and whether the haplotypes are sensitive or resistant.

4.1 Dynamics at the neutral locus

As before p denotes the frequency of the resistant allele 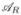. We have p = p₃ + p₄. Moreover, we denote the frequency of the neutral allele 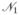among the sensitive and resistant haplotypes by R and Q, respectively. We have $R=\frac{p_1}{p_1+p_2}=\frac{p_1}{1-p}$ and $Q=\frac{p_3}{p_3+p_4}=\frac{p_3}{p}$.

Since $W_1^{(.)}=W_2^{(.)}$ and $W_3^{(.)}=W_4^{(.)}$, λ and μ defined as before become

$$\lambda =\alpha W_3^{(T)}+(1-\alpha )W_3^{(U)}$$ (9a)

and

$$\mu =\alpha W_1^{(T)}+(1-\alpha )W_1^{(U)}.$$ (9b)

From now on we will always assume that the resistant allele becomes fixed, i.e., λ > μ.

Let the frequencies of 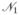among sensitive and resistant parasites at generation t be denoted by R_t and Q_t, respectively. We derive expressions for R_t and Q_t in Appendix A.2. Since the sensitive allele goes extinct in the population, the equilibrium frequency of the neutral allele 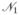is given by

$${\widehat{Q}}^{(m)}=\underset{t\to \infty }{lim}{Q}_t=Q_0+(R_0-Q_0)A(r),$$ (10)

where

$$A(r)=\frac{r}{\lambda }\sum _{\tau =0}^{\infty }\frac{{\vartheta }_{p_{\tau },m}}{\frac{p_0}{1-p_0}{\left(\frac{\lambda }{\mu }\right)}^{\tau }+1}\prod _{l=0}^{\tau -1}{\mathrm{\Lambda }}_{m,l}$$ (11)

$${\vartheta }_{p_t,m}={\left(\frac{p_0}{1-p_0}{\left(\frac{\lambda }{\mu }\right)}^t+1\right)}^{2-m}\sum _{k=0}^{m-2}\left(\begin{array}{c}m-2\\ k\end{array}\right){\theta }_{k,m}{\left(\frac{p_0}{1-p_0}\right)}^k{\left(\frac{\lambda }{\mu }\right)}^{tk},$$ (12)

and

$${\mathrm{\Lambda }}_{m,t}:=1-r\frac{{\vartheta }_{p_t,m}}{\lambda \mu }\left(\frac{p_0{\lambda }^{t+1}+(1-p_0){\mu }^{t+1}}{p_0{\lambda }^t+(1-p_0){\mu }^t}\right).$$ (13)

If we set m = 1 in the above formula we obtain Q̂⁽¹⁾ = Q₀. This is intuitively clear, because there is no recombination and hence the initial proportions of the neutral allele among genotypes with the resistant allele remain constant over time. Note further that in the case m = 2, (10) has a simpler structure because ϑ_pτ,2 = ϑ is a constant.

We summarize:

Result 3

The frequencies of the neural allele 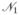among resistant and sensitive haplotypes in generation t are

$$Q_t=Q_0+\frac{r(R_0-Q_0)}{\lambda }\sum _{\tau =0}^{t-1}\frac{{\vartheta }_{p_{\tau },m}}{\frac{p_0}{1-p_0}{\left(\frac{\lambda }{\mu }\right)}^{\tau }+1}\prod _{l=0}^{\tau -1}{\mathrm{\Lambda }}_{m,l}$$ (14)

and

$$R_t=R_0-\frac{r(R_0-Q_0)}{\lambda }\sum _{\tau =0}^{t-1}\frac{{\vartheta }_{p_{\tau },m}}{\frac{1-p_0}{p_0}{\left(\frac{\mu }{\lambda }\right)}^{\tau }+1}\prod _{l=0}^{\tau -1}{\mathrm{\Lambda }}_{m,l}.$$ (15)

If the resistant allele becomes fixed, i.e., if λ > μ, the equilibrium frequency of 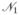is given by (10).

Together with (3) the above result permits us to derive the frequencies of the various haplotypes in each generation. Unfortunately, the equilibrium frequency of 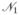does not have an explicit expression but is given by a series. However, since Result 2 yields the time to quasi-fixation, the frequency of 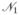at the time point when the resistant allele is almost fixed is given by a finite sum. By proceeding this way we obtain a good estimate for the equilibrium frequency of 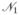. Since resistance usually emerges within a few decades, biologically meaningful times are of the order of at most a few hundred generations, it is not very computational demanding to derive the frequency of 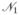at the time of quasi-fixation. Note however that (14) becomes computationally more demanding for larger m.

Furthermore, note that (10) and (14) have a similar but a more complex structure than the corresponding frequencies in the standard-haploid selection model studied by Maynard Smith and Haigh (1974). The differences results from the fact that the recombination between sensitive and resistant parasites, which leads to the decay of genetic hitchhiking, depends on the strength of selection within the host because only parasites exiting the same host recombine. In particular, selection and recombination cannot be decoupled in our model. On the other hand, in the previous (standard) models of hitchhiking, the recombination rate between chromosomes carrying the beneficial and the wild-type allele only depends on their relative frequencies.

4.2 Equilibrium heterozygosity and the hitchhiking effect

The equilibrium heterozygozity (among chromosomes carrying the resistant allele) is given by

$${\widehat{H}}^{(m)}=2{\widehat{Q}}^{(m)}(1-{\widehat{Q}}^{(m)}).$$ (16)

Let us regard the initial frequency of the neutral allele 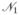initially associated with the sensitive allele, R₀, as a random variable and the heterozygosity as a function of R₀.

The equilibrium frequency of 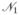is given by (11), where A is a function of the recombination rate that does not depend on R₀. We have

$${\widehat{H}}^{(m)}={\widehat{H}}^{(m)}(R_0)=2(Q_0+(R_0-Q_0)A(r))(1-Q_0-(R_0-Q_0)A(r)).$$ (17)

Now, consider a mutation that initially occurs in a single copy (that is initially rare). Consequently, given the initial frequency of the neutral alleles 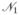is R₀, the beneficial mutation occurs initially in association with the allele 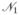(Q₀ = 1) with probability R₀ and in association with allele 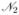(Q₀ = 0) with probability 1 − R₀. Hence, the average heterozygosity is calculated to be

$$\text{E}({\widehat{H}}^{(m)})=\text{E}(\text{E}({\widehat{H}}^{(m)}\mid R_0))=2(\text{E}(R_0)-\text{E}(R_0^2))(2A(r)-A^2(r)).$$ (18)

Since the initial heterozygosity is given by H₀ = 2R₀(1 − R₀), the ratio of the average equilibrium heterozygosity over the average initial heterozygosity as a function of the recombination rate is given by

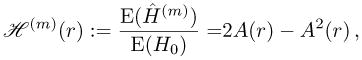(19)

which is independent of the distribution of R₀. Furthermore, since A(0) = 0, we have ℋ^(m)(0) = 0.

Result 4

Given that the resistant allele is initially rare (occurs initially as a single copy), the average relative heterozygosity ℋ^(m)(r), i.e., the ratio of the expected equilibrium heterozygosity at the neutral locus over the expected initial heterozygosity at the neutral locus given by (19), is independent of the initial frequency distribution at the neutral locus. Furthermore, we have ℋ^(m)(0) = 0.

Note that it is crucial in our derivation of ℋ^(m) to assume that the initial frequency of the mutant is rare, i.e., that given R₀ we have Q₀ = 1 and Q₀ = 0 with probabilities R₀ and 1 − R₀, respectively. If this assumption is violated, ℋ^(m) will depend on the distribution of R₀ and the conditional distributions of Q₀ given R₀. Furthermore, ℋ^(m)(0) = 0 does not hold in general.

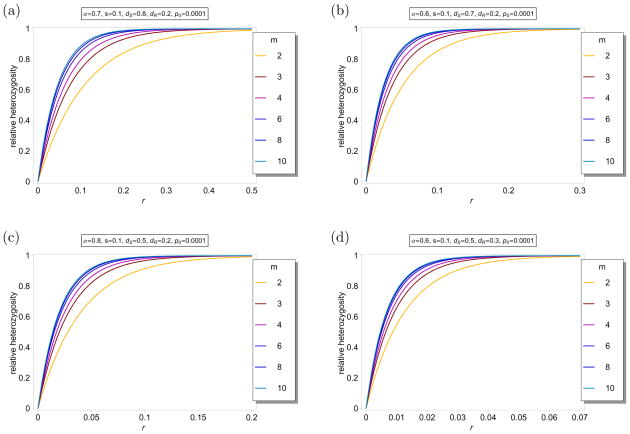
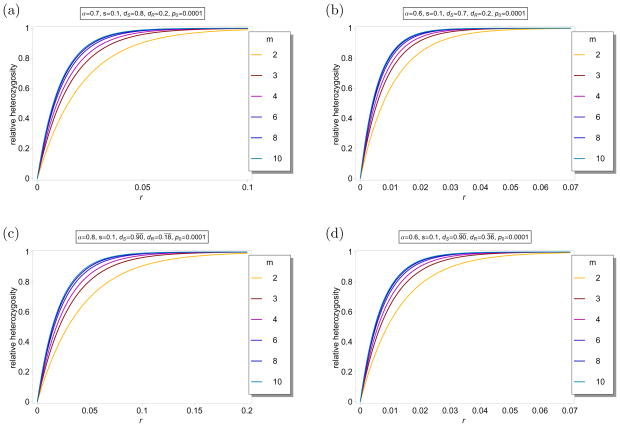
Figure 6 shows ℋ^(m)(r) as a function of r for different parameters and different values for m. As expected ℋ^(m)(r) is monotonically increasing as a function of m. This is intuitively clear, because recombination is less restricted by larger m. Note further that the differences in ℋ^(m) are very small for m ≥ 4.

Figure 6.

Average relative heterozygosity ℋ^(m)(r) as a function of r for different values of m. The fitnesses are parameterized according to (5). The parameters are indicated in the different label panels. Note the different scaling of the x-axes in the different plot panels.

5 Host heterogeneity

The division in treated and untreated hosts in our model is very simplistic, since it assumes that parasites experience the same selection pressures among all treated hosts, and among all untreated hosts. In real populations human hosts will be infected at different times and therefore receive drug treatment at different time points. They will receive different drug concentrations, which will decay individually, at different stages of their infection, and they will respond differently to their individual treatment. More generally, hosts are heterogeneous in real populations. We will now show how our model can be extended to incorporate host heterogeneity.

Assume again a fixed proportion α of hosts is treated. We divide the treated and untreated hosts into various different discrete “treated classes” and “untreated classes”. Let the proportion of infected hosts that fall into class j (j ∈ ℕ) be α_j. Let ⊆ ℕ and = ℕ\ be the sets of untreated and treated, respectively. Hence, we have ${\displaystyle \sum _{j\in \mathbb{U}}}{\alpha }_j=1-\alpha$ and ${\displaystyle \sum _{j\in \mathbb{T}}}{\alpha }_j=\alpha$. Let us denote the fitnesses of parasite haplotypes carrying the sensitive and resistant allele in hosts that fall into class j by $W_1^{(j)}$ and $W_2^{(j)}$, and $W_3^{(j)}$ and $W_4^{(j)}$, respectively.

By incorporating host heterogeneity, the average fitness of resistant and sensitive parasites among treated and untreated hosts become

$$\lambda =\sum _{j=0}^{\infty }{\alpha }_j{W}_3^{(j)}$$ (20a)

and

$$\mu =\sum _{j=0}^{\infty }{\alpha }_j{W}_1^{(j)}.$$ (20b)

If host heterogeneity is incorporated, Result 2 holds unchanged, with λ and μ given by (20a) and (20b). Therefore, regarding the spread of resistance, modeling host heterogeneity results only in an adjustment of fitnesses.

Most of the derivations of Section 4 remain valid for the model which incorporates host heterogeneity. In fact, the equilibrium frequency of the neutral allele is again given by formula (10), but with λ, μ, ϑ_p,m and Λ_m,t properly adjusted. The parameters λ and μ are given by (20a) and (20b), whereas ϑ_p,m and Λ_m,t are still given by (12) and (13), however in (12) θ_k,m has to be replaced by

$${\theta }_{k,m}=(m-1)\sum _{j=0}^{\infty }\frac{{\alpha }_j{W}_1^{(j)}{W}_3^{(j)}}{(m-1-k)W_1^{(j)}+(k+1)W_3^{(j)}}.$$ (21)

Hence, again the only effect of host heterogeneity results just in an adjustment of the parameters for the hitchhiking effect. In fact, the equilibrium frequency of the neutral allele 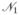has again the form (10). Therefore, we have:

Result 5

Results 1, 2, 3 and 4 hold also in the model accounting for host heterogeneity with λ, μ and θ_k,m given by (20a), (20b) and (21), respectively.

We shall illustrate the effect of treatment time by the following example.

Example 3

Assume drug concentration is measured in discrete units and that parasites in a host encounter at most N units of drug concentration. Let the fitnesses of sensitive and resistant parasites in hosts that carry a dosage of j concentration units be

$$W_1^{(j)}=W_2^{(j)}=1-\frac{{jd}_S}{N}$$

and

$$W_3^{(j)}=W_4^{(j)}=1-s-\frac{{jd}_R}{N},$$

respectively. Hence, parasites in untreated hosts have the fitnesses $W_1^{(0)}=1$ and $W_3^{(0)}=1-s$ as in the original model. Moreover, parasites in hosts with maximum drug concentration (N units) have fitnesses $W_1^{(N)}=1-d_S$ and $W_3^{(N)}=1-s-d_R$, again as in the original model, with d_R replaced by d_R + s.

As usual let α₀ = 1 − α denote the proportion of untreated hosts. Furthermore, assume ${\alpha }_j=\frac{\alpha }{N}$ for j ≥ 1, i.e., the various levels of drug concentration are uniformly distributed among hosts. Hence, we have $\lambda =1-s-\alpha \frac{d_R}{2}(1+\frac{1}{N})$ and $\mu =1-\alpha \frac{d_S}{2}(1+\frac{1}{N})$.

Figure 7 illustrates this example. The figure shows ℋ^(m)(r) as a function of r for different parameter combinations and different values of m. Comparison of Figures 7a, b with Figures 6a, b shows that the hitchhiking effect is greatly reduced. The reason is that the sweep of the resistant allele is slowed down because it is only weakly advantageous in hosts with low drug concentration, so that recombination breaks down the initial association of the resistant allele and the linked neutral allele. In Figures 7c, d the values of parameters λ and μ are identical to those in Figures 6c, d, respectively. In particular, the dynamics at the selected locus are identical in the corresponding cases. Comparison of the figures shows that the hitchhiking effect is slightly increased with host heterogeneity.

Figure 7.

Average relative heterozygosity ℋ^(m)(r) as a function of r for different values of m for the model accounting for host heterogeneity. The fitnesses are chosen as in Example 3, with N = 10. Hence, there are eleven host classes. The parameters are indicated in the different panels. In figures (a) and (b), the parameters are chosen as in Figures 6(a), and (b), respectively. In figures (c) and (d), the parameters are chosen such that λ and μ are equal to the corresponding values in Figures 6(c), and (d), respectively.

We can give this example different alternative interpretations. For instance, α_j can be the proportion of hosts that receive drug treatment for j time units, or as the proportion of hosts in which the drug level decayed after j time units.

6 Number of co-infections

Another assumption that is simplified in the original formulation of our model is the fact that all hosts are infected by the same number m of parasites. This is of course oversimplified, because a host might be co-infected by several mosquitoes. In a real population the number m of parasites that infect a host will follow some probability distribution κ over the whole population. Our model can be easily extended to take this into account.

Let κ_m denote the probability that a host is infected by m ≥ 1 parasites. Naturally, we have ${\displaystyle \sum _{m=1}^{\infty }}{\kappa }_m=1$. Clearly, since the trajectory of the resistant allele at the selected locus is independent of the number m, the dynamics of the resistant allele is still given by (28). Hence, the dynamics of the sweep of the resistant allele does not change. However, if one also wants to incorporate different classes of treated and untreated hosts, the parameters have to be adjusted as described in Section 5.

For the hitchhiking effect we have to account for the distribution of m. However, it is straightforward to see how to adapt the derivations in the general case. We obtain

$$Q_t=Q_0+\frac{r(R_0-Q_0)}{\lambda }\sum _{\tau =0}^{t-1}\frac{1}{\frac{p_0}{1-p_0}{\left(\frac{\lambda }{\mu }\right)}^{\tau }+1}{\vartheta }_{p_{\tau },\kappa }\prod _{l=0}^{\tau -1}{\mathrm{\Lambda }}_{\kappa ,l}$$ (22a)

and

$$R_t=R_0-\frac{r(R_0-Q_0)}{\mu }\sum _{\tau =0}^{t-1}\frac{1}{\frac{1-p_0}{p_0}{\left(\frac{\mu }{\lambda }\right)}^{\tau }+1}{\vartheta }_{p_{\tau },\kappa }\prod _{l=0}^{\tau -1}{\mathrm{\Lambda }}_{\kappa ,l},$$ (22b)

where

$${\vartheta }_{p_t,\kappa }:=\sum _{m=0}^{\infty }{\kappa }_m{\vartheta }_{p_t,m},$$ (23)

and

$${\mathrm{\Lambda }}_{\kappa ,t}:=\sum _{m=0}^{\infty }{\kappa }_m{\mathrm{\Lambda }}_{m,t}.$$ (24)

The equilibrium frequency of the neutral allele is given by

$${\widehat{Q}}^{(\kappa )}=\underset{t\to \infty }{lim}{Q}_t.$$ (25)

Host heterogeneity as described in Section 5 can be incorporated by making the adjustments described in that section. Since Q̂⁽¹⁾ ≡ Q₀ it follows that there will be a genome-wide reduction in relative heterozygosity if κ₁ is sufficiently large. The reason is that a fraction κ₁ of parasites behave clonally in the mosquito vector.

Clearly, Q̂^(κ) has again the form Q̂^(κ) = Q₀ + (R₀ − Q₀)A(r), where A(r) is a proper function of the recombination rate with A(0) = 0. Hence, the fraction of the expected equilibrium heterozygosity over the expected initial heterozygosity, now denoted by ℋ^(κ)(r) is again independent from the distribution of R₀, if the resistant allele is initially rare. We summarize:

Result 6

In the case in which the number of parasites infecting a host is not constant but follows some distribution, Results 1 and 2 hold without changes. Result 3 holds with Q_t and R_t given by (22) and with Q̂^(m) replaced by Q̂^(κ) given by (25). Furthermore, Result 4 holds for ℋ^(κ).

The same statements remain valid if additionally host heterogeneity is incorporated, but with λ, μ and θ_k,m adjusted as described in Result 5.

We shall illustrate the effect of the distribution κ on the equilibrium heterozygosity in the next example.

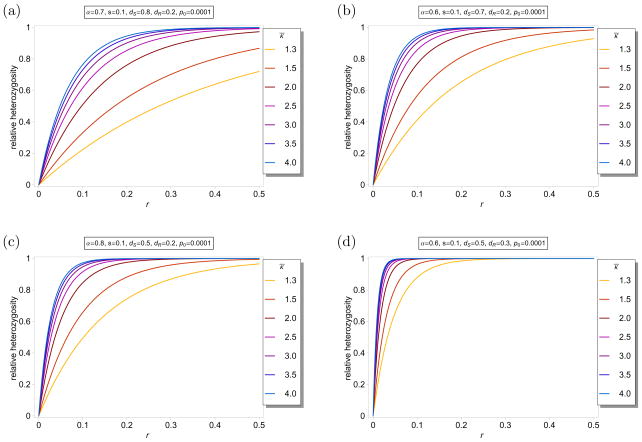
Example 4

Assume that a host gets infected by at most ten different parasites. The number of parasites infecting a host is assumed to follow a truncated Poisson distribution with parameter κ̄, i.e., ${\kappa }_m=e^{-\overline{\kappa }}\frac{{\overline{\kappa }}^{m-1}}{(m-1)!}$ for m ∈ {1, …, 9} and ${\kappa }_{10}=e^{-\overline{\kappa }}{\displaystyle \sum _{m=10}^{\infty }}\frac{{\overline{\kappa }}^{m-1}}{(m-1)!}$. Figure 8 shows ℋ^(κ)(r) as a function of r for different parameters κ̄ and different selection parameters. The selection parameters are chosen as in Figure 6 to make comparisons easier. As seen from comparison with Figure 6 ℋ^(κ)(r) is significantly reduced. The reason is that parasites solely infecting hosts cannot undergo recombination with other haplotypes. Therefore, even with the maximum distance (r = 0.5) on the genetic map, the effective recombination rate decreases below 0.5 by the fraction of the hosts with m = 1.

Figure 8.

Average relative heterozygosity ℋ^(κ)(r) as a function of r for different distributions for κ as described in Example 4. The parameters are chooses as in Figure 6.

From the figure it is immediately apparent how strongly recombination is restricted by the nature of the transmission cycle. Because of the transmission cycle a high degree of selfing occurs among treated hosts. Note further that (for strong selection) the genome-wide reduction of the relative heterozygosity (ℋ^(κ)(0.5) < 1), which is caused mainly by the fraction κ₁ of hosts that are infected by a single parasite. This results in strict selfing in a fraction κ₁ of hosts, and the involved parasites behave like they reproduce clonally in the mosquito vector.

Note that ℋ^(κ) depends crucially on the characteristics of the distribution κ, not just on its mean value. For instance the hitchhiking effect will be much more pronounced if κ attains the values 1 and 3 with probability $\frac{1}{2}$ each, than if κ ≡ 2. In particular, in the first case there will be a much wider reduction of relative heterozygosity, whereas this will not hold true in the second case.

7 Discussion

In this article, we developed a deterministic, analytically feasible model for the spread of drug resistance among human malaria parasites. The model is simple enough to be treated analytically although it covers the most important properties of the malaria transmission cycle. Unlike in previous work, e.g., Dye and Williams (1997), Mackinnon and Hastings (1998), our model is based on exact equations. For instance, Mackinnon and Hastings (1998) use only approximate formulas to account for the effect of selfing inherent in the transmission cycle by arguing that the exact formulas have not been derived yet. Notably our model also incorporates drug efficiency on both sensitive and resistant parasites, because selection is formulated in terms of absolute fitnesses. However, since we are only interested in the relative frequencies of the various haplotypes, fitnesses can be normalized such that the maximum fitness (typically that of sensitive haplotypes in untreated hosts) equals one. This relies on the assumption that the parasites population is sufficiently (infinitely) large. Novel to our approach is that our model permits us to study genetic hitchhiking. In the context of drug resistance among malaria parasites, genetic hitchhiking was studied so far only to identify targets of selection to clarify the genetic basis of resistance against various drugs (see e.g. Wootton et al., Nair et al. 2003; cf. Escalante et al., 2004). Hence, hitchhiking was studied in an empirical rather than in a theoretical context. By providing a model for the spread of resistance that allows us to study genetic hitchhiking, it is possible to validate model parameters based on the pattern of neutral genetic variation observed in empirical data. This approach will lead to refined parameters and more accurate predictions.

Our model is feasible as we assume resistance is caused by a mutation at a single locus. It appears that more than one locus was involved in the evolution of CQ and SP resistance. However, as long as a single mutation in one of those loci increases the fitness of parasites under drug treatment (i.e. the additive effect of the mutation is advantageous), its qualitative evolutionary dynamics and the associated hitchhiking effect will be compatible with our model.

In the basic formulation our model has two critical parameters, the proportion of treated hosts, α, and the number of parasites infecting a host, m, that are believed to play major roles in producing unique evolutionary dynamics specific to a given demographic setting. The parameter α is determined mostly by host-acquired immunity, which leads to asymptomatic infections that will consequently remain untreated (Hastings, 2004), and by drug-treatment policies. High levels of host-acquired immunity typically occur in geographical areas with high transmission intensities (which are correlated with high prevalence), such as sub-Saharan Africa or Papua New Guinea, in which hosts are usually infected multiple times during their life span (cf. Escalante et al., 2002b; Hastings et al., 2002; Hastings, 2003, 2004). Such population should therefore be modeled with a small value of α. On the contrary, in areas of low transmission, e.g., Southeast Asia, host-acquired immunity is low, and almost all malaria infections are symptomatic (Hastings et al., 2002; Hastings, 2003, 2004), leading to large α.

The number m of parasites causing an infection reflects the number of co-infections acquired by a host. Hence, m will be larger in areas of high transmission (cf. Hastings et al., 2002; Hastings, 2003). Estimates for m were typically between 1 and 7 (cf. Arnot, 1998; Anderson et al., 2000; Hastings, 2006). In areas of high transmission rates a typical human may have between 3 and 7 genetically distinct parasite clones simultaneously circulating in the blood (cf. Arnot, 1998). The smaller the parameter m the larger is the degree of selfing among parasites in the mosquito vector. If m = 1, there is complete selfing and the parasites behave like a clonal population.

Our model is expandable such that m does not need to be a fixed integer valued parameter, but it is allowed to follow some frequency distribution. This is extremely important for testing the model against empirical data, if the average number of co-infections and its variance are known. Furthermore, our model can be generalized to incorporate host heterogeneity. This extension can be used to model drug-concentration levels, drug decay, treatment time, individual immune response etc. With the interpretation of different classes of treated and untreated hosts, it becomes apparent that our model does not only apply to human malaria parasites, but can be applied to model host switches.

Under the assumption that resistance is caused by a single allele, we were able to derive conditions for the spread of the resistant allele. In particular, we established an explicit solution for the dynamics of the resistant allele, a formula for the time until a given level of resistance is reached, and especially for the time to quasi-fixation. These results are valuable for public-health policies to estimate how long it will take until an unacceptable high degree of drug resistance is reached. Since we do not model intra-host competition of parasites, all these results are independent of the number of parasites infecting a host.

In the basic model of Section 2.1, our results clearly show that the conditions for the spread of resistance are less restrictive for large α. Moreover, the speed of resistance spread is increasing with α. Hence, it is plausible that resistant alleles, especially with high metabolic costs, are more likely to spread in areas of low transmission, or in areas of low host-acquired immunity. Empirically, this is confirmed by the fact that the resistant allele at the CQ-resistance determining locus pfcrt found in Africa originated from Asia, a low transmission area (cf. Roper et al., 2003). Similarly, Pyrimethamine resistance in Africa originated from Southeast Asia (cf. Roper et al., 2004), and SP resistance was first reported on the Thai-Cambodian border (cf. Wongsrichanalai et al., 2002).

Moreover, we are able to study the hitchhiking effect of the resistant allele sweeping through the parasite population. Studying genetic hitchhiking in malaria parasites requires a new theoretical approach because standard hitchhiking theory cannot be applied accurately because of two related reasons. The first one is rooted in the transmission cycle itself: Because recombination between malaria parasites occurs in the mosquito’s gut immediately after its blood meal, only parasites originating from the same host recombine (cf. Cornejo and Escalante, 2006). This leads to a high degree of selfing, which greatly limits the opportunity of newly-emerged resistant alleles to recombine with neutral alleles on other (sensitive-allele carrying) chromosomes. The severity of the effect of selfing is mainly determined by the number of different parasite haplotypes in the human host, which in turn depends on the number of co-infections (cf. Dye and Williams, 1997).

The second reason is that selection on parasites acts differently in treated and untreated hosts. The resistant allele will be advantageous in treated hosts, but likely to be slightly deleterious among untreated hosts due to metabolic costs (cf. Wolstenholme et al., 2004; Hastings, 2006). One may suggest that the standard hitchhiking model may be used by substituting the selective advantage of the resistant allele with the average fitness over treated and untreated hosts. However, such application is incorrect because the effective recombination rate (which depends on the probability that a resistant haplotype exits an infected host together with a sensitive haplotype) is different between treated and untreated hosts. Unlike the standard hitchhiking model, the processes of recombination and selection cannot be specified separately. The effective recombination rate is low with strong drug pressure in treated hosts. For a similar reason, intra-host competition among co-infecting parasite clones will also reduce the effective rate of recombination between sensitive and resistant parasites. Therefore, since our model assumes no intra-host competition (“specific immunity”; Hastings, 1997), the effect of genetic hitchhiking will be greater than our analytic prediction if intra-host competition exists.

We were able to provide a solution for the dynamics at a linked neutral locus as a function of the meiotic recombination rate. The results are valid for arbitrary initial frequencies of the resistant allele and any degree of linkage disequilibrium between the selected and the neutral locus. Unfortunately, the dynamics at the linked neutral locus does not admit an explicit solution (cf. Maynard Smith and Haigh, 1974). Especially, the equilibrium frequencies at the neutral locus are given only as limits. However, for practical purposes it is sufficient to derive the frequencies at the neutral locus at the time of quasi-fixation (for which we have an explicit formula). Hence, approximately, the equilibrium frequencies are given by finite sums. Anyway, accurate approximations for the hitchhiking effect that admit a simple closed form are highly desirable, and will be derived in a follow-up paper.

The number of parasites infecting a host has a large effect on the pattern of neutral genetic variations, since this parameter is linked to the degree of selfing of the parasites. This will be especially apparent if the proportion of hosts that are infected by a single haplotype is large. Note however, that the number of parasites co-infecting a host has no effect on the spread of resistance.

In the basic model for different values of m, the differences in the average relative heterozygosity become negligible if m is larger than four. The hitchhiking effects becomes less pronounced as m increases. If m = 1, then there is complete selfing among parasites, so all neutral variation will vanish. For the more general model in which m follows a frequency distribution, it seems to be appropriate to assume that m takes only values from one to at most ten. Remarkable if a large fraction of hosts is infected by a single parasite, i.e., κ₁ is sufficiently large, a genome-wide reduction of heterozygosity will be observed for sufficiently strong selection. Genome-wide reduction of variation by the combined effect of hitchhiking and selfing was first reported by Hedrick (1980).

The genome-wide reduction of relative heterozgosity in our model is due to the assumption that the resistant allele has a single origin. If it had multiple origins this will no longer be true. However, for data analysis, it would be sufficient consider only resistant parasites that have the same mutational origin. Moreover, the assumption of a single mutational origin is appropriate for malaria. For SP and CQ resistance it is known that three to four point mutations have to occur in the same gene to cause a significant level of resistance. Genealogical analyses show that in all endemic areas single or double mutations with different origins occur, but triple mutations have typically only one origin. Hence, if haplotypes carrying single or double mutations are subsumed as sensitive, the assumption of a single origin is fulfilled.

Clearly, the number of co-infections will be larger in areas of high transmission. Thus, it is plausible that the effect of genetic hitchhiking is more severe in areas of low transmission (cf. Shi et al., 1992; Anderson et al., 2000; Escalante et al., 2001, 2002a,b). Since the spread of resistance occurs faster if a large proportion of hosts is treated, the hitchhiking effect is more pronounced for large α. Because selfing among resistant parasites occurs more frequently in treated than in untreated hosts, large α also effectively reduces the recombination rate. Hence, again in areas of low transmission, the detectable pattern of selection should be more pronounced.

We also gave examples illustrating how the hitchhiking pattern will be affected by different drug concentration levels, or treatment time. To be able to fully understand this relation it would be necessary to have more knowledge about realistic assumptions on the involved parameters. This, however, is beyond the scope of this article. Anyhow, our results suggest that incorporating different levels of drug concentration results in a slightly more pronounced hitchhiking pattern than suggested by the basic model with comparable parameters that lead to the same fixation time.

In general, we expect our deterministic approach to underestimate the hitchhiking effect. The initial spread of a rare allele causing resistance is stochastic. Conditioned on fixation of such a mutation, the initial spread will be quicker than suggested by the deterministic model (?). Hence, a stochastic version of our model would be highly desirable and is planned for future work.

A next step, which is planned for future work, is to evaluate the accuracy of our model by testing it against empirical data. By using estimates for the proportion of treated hosts, number of co-infections, metabolic costs, and selection parameters, it should be possible to test whether the pattern of genetic hitchhiking in natural populations is in agreement with the predictions of our model.

A Appendix

A.1 Fixation of an allele causing resistance

The absolute frequency p^*(.) of the resistant allele 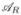in the mosquito population that have taken their blood meal from treated or untreated hosts is calculated by marginalization of the dynamics of Section 2. Straightforward calculation yields

$$p^{\ast (.)}=\sum _{i=0}^m\left(\begin{array}{c}m\\ i\end{array}\right)p^i{(1-p)}^{m-i}\frac{\gamma }{m}\left[\frac{i^2{w}_R^{{(.)}^2}+2\frac{1}{2}i(m-i)w_R^{(.)}{w}_S^{(.)}+0{(m-i)}^2{w}_S^{{(.)}^2}}{i{w}_R^{(.)}+(m-i)w_S^{(.)}}\right]$$ (26a)

$$=\sum _{i=0}^m\left(\begin{array}{c}m\\ i\end{array}\right)p^i{(1-p)}^{m-i}\frac{\gamma }{m}\left[\frac{i{w}_R^{(.)}(i{w}_R^{(.)}+(m-i)w_S^{(.)}}{i{w}_R^{(.)}+(m-i)w_S^{(.)}}\right]$$ (26b)

$$=\sum _{i=0}^m\left(\begin{array}{c}m\\ i\end{array}\right)p^i{(1-p)}^{m-i}\frac{\gamma }{m}i{w}_R^{(.)}=\gamma w_R^{(.)}\sum _{i=1}^m\frac{(m-1)!}{(i-1)!(m-i)!}{p}^i{(1-p)}^{m-i}$$ (26c)

$$=\gamma p{w}_R^{(.)}\sum _{i=1}^m\frac{(m-1)!}{(i-1)!(m-i)!}{p}^{i-1}{(1-p)}^{m-i}=\gamma p{w}_R^{(.)}\sum _{i=0}^{m-1}\frac{(m-1)!}{i!(m-i)!}{p}^i{(1-p)}^{m-1-i}$$ (26d)

$$=\gamma p{w}_R^{(.)}.$$ (26e)

Similarly we have

$${(1-p)}^{\ast (.)}=\gamma (1-p)w_S^{(.)}.$$ (27)

From this we immediately obtain

$$p^{\prime }=\frac{p\lambda }{p\lambda +(1-p)\mu },$$ (28)

where λ and μ are defined in (4). Iterating (28) gives

A.2 Dynamics at the neutral locus

For the case in which there is only one selected, and one neutral locus, the absolute frequency of the first gamete in the mosquito population that have taken their blood meal from treated or untreated hosts is calculated to be

$$\begin{array}{l}{p}_1^{\ast (.)}=\sum _{\mid \mathit{m}\mid =m}\left(\begin{array}{c}m\\ \mathit{m}\end{array}\right)\frac{\gamma }{m}{\mathit{p}}^{\mathit{m}}\sum _{k,l=1}^4\frac{m_k{W}_k^{(.)}{m}_l{W}_l^{(.)}}{W_{\mathit{m}}^{(.)}}R(k,l\to 1)\\ =\frac{\gamma }{m}\sum _{\mid \mathit{m}\mid =m}\left(\begin{array}{c}m\\ \mathit{m}\end{array}\right)\frac{{\mathit{p}}^{\mathit{m}}}{W_{\mathit{m}}^{(.)}}\left(m_1^2{W}_1^{{(.)}^2}+m_1{m}_2{W}_1^{(.)}{W}_2^{(.)}+m_1{m}_3{W}_1^{(.)}{W}_3^{(.)}+m_1{m}_4{W}_1^{(.)}{W}_4^{(.)}(1-r)+m_2{m}_3{W}_2^{(.)}{W}_3^{(.)}r\right).\end{array}$$

Making use of $W_1^{(.)}=W_2^{(.)}$ and $W_3^{(.)}=W_4^{(.)}$, the above becomes

$$\begin{array}{l}{p}_1^{\ast (.)}=\frac{\gamma }{m}{W}_1^{(.)}\sum _{\mid \mathit{m}\mid =m}\left(\begin{array}{c}m\\ \mathit{m}\end{array}\right)\frac{{\mathit{p}}^{\mathit{m}}}{W_{\mathit{m}}^{(.)}}\left(m_1^2{W}_1^{(.)}+m_1{m}_2{W}_2^{(.)}+m_1{m}_3{W}_3^{(.)}+m_1{m}_4{W}_4^{(.)}(1-r)+m_2{m}_3{W}_3^{(.)}r\right)\\ =\frac{\gamma }{m}{W}_1^{(.)}\sum _{\mid \mathit{m}\mid =m}\left(\begin{array}{c}m\\ \mathit{m}\end{array}\right)\frac{{\mathit{p}}^{\mathit{m}}}{W_{\mathit{m}}^{(.)}}\left(m_1(m_1{W}_1^{(.)}+m_2{W}_2^{(.)}+m_3{W}_3^{(.)}+m_4{W}_4^{(.)})+r(m_2{m}_3{W}_3^{(.)}-m_1{m}_4{W}_4^{(.)})\right)\\ =\frac{\gamma }{m}{W}_1^{(.)}\sum _{\mid \mathit{m}\mid =m}\left(\begin{array}{c}m\\ \mathit{m}\end{array}\right)\frac{{\mathit{p}}^{\mathit{m}}}{W_{\mathit{m}}^{(.)}}\left(m_1{W}_{\mathit{m}}^{(.)}+r{W}_3^{(.)}(m_2{m}_3-m_1{m}_4)\right)\\ =\frac{\gamma }{m}{W}_1^{(.)}\sum _{\begin{array}{c}\mid \mathit{m}\mid =m\\ m_1>0\end{array}}\frac{m!p_1^{m_1}{p}_2^{m_2}{p}_3^{m_3}{p}_4^{m_4}}{m_1!m_2!m_3!m_4!}{m}_1+\gamma r{W}_1^{(.)}{W}_3^{(.)}\sum _{\mid \mathit{m}\mid =m}\left(\begin{array}{c}m\\ \mathit{m}\end{array}\right)\frac{{\mathit{p}}^{\mathit{m}}}{W_{\mathit{m}}^{(.)}}\left(m_2{m}_3-m_1{m}_4\right)\\ =p_1\gamma W_1^{(.)}\sum _{\begin{array}{c}\mid \mathit{m}\mid =m\\ m_1>0\end{array}}\frac{(m-1)!p_1^{m_1-1}{p}_2^{m_2}{p}_3^{m_3}{p}_4^{m_4}}{(m_1-1)!m_2!m_3!m_4!}+\frac{\gamma }{m}r{W}_1^{(.)}{W}_3^{(.)}\sum _{\mid \mathit{m}\mid =m}\left(\begin{array}{c}m\\ \mathit{m}\end{array}\right)\frac{{\mathit{p}}^{\mathit{m}}}{W_{\mathit{m}}^{(.)}}(m_2{m}_3-m_1{m}_4)\\ =p_1\gamma W_1^{(.)}\sum _{\mid \mathit{m}\mid =m-1}\left(\begin{array}{c}m-1\\ \mathit{m}\end{array}\right){\mathit{p}}^{\mathit{m}}+\frac{\gamma }{m}r{W}_1^{(.)}{W}_3^{(.)}\sum _{\mid \mathit{m}\mid =m}\left(\begin{array}{c}m\\ \mathit{m}\end{array}\right)\frac{{\mathit{p}}^{\mathit{m}}}{W_{\mathit{m}}^{(.)}}(m_2{m}_3-m_1{m}_4)\\ =p_1\gamma W_1^{(.)}+\frac{\gamma }{m}r{W}_1^{(.)}{W}_3^{(.)}\sum _{\mid \mathit{m}\mid =m}\left(\begin{array}{c}m\\ \mathit{m}\end{array}\right)\frac{{\mathit{p}}^{\mathit{m}}(m_2{m}_3-m_1{m}_4)}{(m_1+m_2)W_1^{(.)}+(m_3+m_4)W_3^{(.)}}\\ =p_1\gamma W_1^{(.)}+\frac{\gamma }{m}r{W}_1^{(.)}{W}_3^{(.)}\left(p_2{p}_3\sum _{\begin{array}{c}\mid \mathit{m}\mid =m\\ m_2,m_3>0\end{array}}\frac{m!}{m_1!m_2!m_3!m_4!}\frac{p_1^{m_1}{p}_2^{m_2-1}{p}_3^{m_3-1}{p}_4^{m_4}{m}_2{m}_3}{(m_1+m_2)W_1^{(.)}+(m_3+m_4)W_3^{(.)}}-p_1{p}_4\sum _{\begin{array}{c}\mid \mathit{m}\mid =m\\ m_1,m_4>0\end{array}}\frac{m!}{m_1!m_2!m_3!m_4!}\frac{p_1^{m_1-1}{p}_2^{m_2}{p}_3^{m_3}{p}_4^{m_4-1}{m}_1{m}_4}{(m_1+m_2)W_1^{(.)}+(m_3+m_4)W_3^{(.)}}\right)\\ =p_1\gamma W_1^{(.)}+\frac{\gamma }{m}r{W}_1^{(.)}{W}_3^{(.)}m(m-1)\times \left(p_2{p}_3\sum _{\begin{array}{c}\mid \mathit{m}\mid =m\\ m_2,m_3>0\end{array}}\frac{(m-2)!}{m_1!(m_2-1)!(m_3-1)!m_4!}\frac{p_1^{m_1}{p}_2^{m_2-1}{p}_3^{m_3-1}{p}_4^{m_4}}{(m_1+m_2)W_1^{(.)}+(m_3+m_4)W_3^{(.)}}-p_1{p}_4\sum _{\begin{array}{c}\mid \mathit{m}\mid =m\\ m_1,m_4>0\end{array}}\frac{(m-2)!}{(m_1-1)!m_2!m_3!(m_4-1)!}\frac{p_1^{m_1-1}{p}_2^{m_2}{p}_3^{m_3}{p}_4^{m_4-1}}{(m_1+m_2)W_1^{(.)}+(m_3+m_4)W_3^{(.)}}\right)\\ =p_1\gamma W_1^{(.)}+\frac{\gamma }{m}r{W}_1^{(.)}{W}_3^{(.)}m(m-1)\left(p_2{p}_3\sum _{\mid \mathit{m}\mid =m-2}\left(\begin{array}{c}m-2\\ \mathit{m}\end{array}\right)\frac{{\mathit{p}}^{\mathit{m}}}{(m_1+m_2+1)W_1^{(.)}+(m_3+m_4+1)W_3^{(.)}}-p_1{p}_4\sum _{\mid \mathit{m}\mid =m-2}\left(\begin{array}{c}m-2\\ \mathit{m}\end{array}\right)\frac{{\mathit{p}}^{\mathit{m}}}{(m_1+m_2+1)W_1^{(.)}+(m_3+m_4+1)W_3^{(.)}}\right)\\ =p_1\gamma W_1^{(.)}+\frac{\gamma }{m}r{W}_1^{(.)}{W}_3^{(.)}m(m-1)(p_2{p}_3-p_1{p}_4)A,\end{array}$$

where

$$A=\sum _{\mid \mathit{m}\mid =m-2}\left(\begin{array}{c}m-2\\ \mathit{m}\end{array}\right)\frac{{\mathit{p}}^{\mathit{m}}}{(m_1+m_2+1)W_1^{(.)}+(m_3+m_4+1)W_3^{(.)}}.$$

Moreover, we have

$$\begin{array}{l}A=\sum _{k=0}^{m-2}\sum _{m_1=0}^k\sum _{m_3=0}^{m-2-k}\frac{(m-2)!}{m_1!(k-m_1)!m_3!(m-2-k-m_3)!}\frac{p_1^{m_1}{p}_2^{k-m_1}{p}_3^{m_3}{p}_4^{m-2-k-m_3}}{(k+1)W_1^{(.)}+(m-2-k+1)W_3^{(.)}}\\ =\sum _{k=0}^{m-2}\left(\frac{(m-2)!}{k!(m-2-k)!((k+1)W_1^{(.)}+(m-1-k)W_3^{(.)})}\times \sum _{m_1=0}^k\frac{k!}{m_1!(k-m_1)!}{p}_1^{m_1}{p}_2^{k-m_1}\sum _{m_3=0}^{m-2-k}\frac{(m-2-k)!}{m_3!(m-2-k-m_3)!}{p}_3^{m_3}{p}_4^{m-2-k-m_3}\right)\\ =\sum _{k=0}^{m-2}\left(\begin{array}{c}m-2\\ k\end{array}\right)\frac{1}{(k+1)W_1^{(.)}+(m-1-k)W_3^{(.)}}{(p_1+p_2)}^k{(p_3+p_4)}^{m-2-k}\\ =\sum _{k=0}^{m-2}\left(\begin{array}{c}m-2\\ k\end{array}\right)\frac{{(1-p)}^k{p}^{m-2-k}}{(k+1)W_1^{(.)}+(m-1-k)W_3^{(.)}}.\end{array}$$

By using p₂p₃ − p₁p₄ = p(1 − p)(Q − R), we arrive at

$$\begin{array}{l}{p}_1^{\ast (.)}=p_1\gamma W_1^{(.)}+\gamma r{W}_1^{(.)}{W}_3^{(.)}(m-1)p(1-p)(Q-R)\sum _{k=0}^{m-2}\left(\begin{array}{c}m-2\\ k\end{array}\right)\frac{{(1-p)}^k{p}^{m-2-k}}{(k+1)W_1^{(.)}+(m-1-k)W_3^{(.)}}\\ =p_1\gamma W_1^{(.)}+\gamma r{W}_1^{(.)}{W}_3^{(.)}(m-1)p(1-p)(Q-R)\sum _{k=0}^{m-2}\left(\begin{array}{c}m-2\\ k\end{array}\right)\frac{p^k{(1-p)}^{m-2-k}}{(m-1-k)W_1^{(.)}+(k+1)W_3^{(.)}}.\end{array}$$

After performing similar derivations for the remaining haplotypes, we arrive at

$$p_1^{\ast (.)}=p_1\gamma W_1^{(.)}+\gamma rp(1-p)(Q-R){\vartheta }_{p,m}^{(.)},$$ (29a)

$$p_2^{\ast (.)}=p_2\gamma W_1^{(.)}-\gamma rp(1-p)(Q-R){\vartheta }_{p,m}^{(.)},$$ (29b)

$$p_3^{\ast (.)}=p_3\gamma W_3^{(.)}-\gamma rp(1-p)(Q-R){\vartheta }_{p,m}^{(.)},$$ (29c)

$$p_4^{\ast (.)}=p_4\gamma W_3^{(.)}+\gamma rp(1-p)(Q-R){\vartheta }_{p,m}^{(.)},$$ (29d)

where

$$\begin{array}{l}{\vartheta }_{p,m}^{(.)}:=W_1^{(.)}{W}_3^{(.)}\sum _{k=0}^{m-2}\left(\begin{array}{c}m-2\\ k\end{array}\right)\frac{(m-1)p^k{(1-p)}^{m-2-k}}{(m-1-k)W_1^{(.)}+(k+1)W_3^{(.)}}\\ =\sum _{k=0}^{m-2}\left(\begin{array}{c}m-2\\ k\end{array}\right){\theta }_{k,m}^{(.)}{p}^k{(1-p)}^{m-k-2},\end{array}$$ (30)

and

$${\theta }_{k,m}^{(.)}:=\frac{(m-1)W_1^{(.)}{W}_3^{(.)}}{(m-1-k)W_1^{(.)}+(k+1)W_3^{(.)}}.$$ (31)

The absolute frequency of haplotype i in the mosquito population after recombination is given by $p_i^{\ast }:=\alpha p_i^{\ast (T)}+(1-\alpha )p_i^{\ast (U)}$. Let

$${\vartheta }_{p,m}=\alpha {\vartheta }_{p,m}^{(T)}+(1-\alpha ){\vartheta }_{p,m}^{(U)}=\sum _{k=0}^{m-2}\left(\begin{array}{c}m-2\\ k\end{array}\right){\theta }_{k,m}{p}^k{(1-p)}^{m-2-k},$$ (32)

with

$${\theta }_{k,m}:=\alpha {\theta }_{k,m}^{(T)}+(1-\alpha ){\theta }_{k,m}^{(U)}.$$ (33)

Hence, we obtain

$$\begin{array}{l}{p}_1^{\ast }=p_1\gamma \mu +\gamma rp(1-p)(Q-R){\vartheta }_{p,m},\\ p_2^{\ast }=p_2\gamma \mu -\gamma rp(1-p)(Q-R){\vartheta }_{p,m},\\ p_3^{\ast }=p_3\gamma \lambda -\gamma rp(1-p)(Q-R){\vartheta }_{p,m},\\ p_4^{\ast }=p_4\gamma \lambda +\gamma rp(1-p)(Q-R){\vartheta }_{p,m}.\end{array}$$

The above implies the following identities

$$\overline{W}{p}_1^{\prime }=p_1\mu +rp(1-p)(Q-R){\vartheta }_{p,m},$$ (35a)

$$\overline{W}{p}_2^{\prime }=p_2\mu -rp(1-p)(Q-R){\vartheta }_{p,m},$$ (35b)

$$\overline{W}{p}_3^{\prime }=p_3\lambda -rp(1-p)(Q-R){\vartheta }_{p,m},$$ (35c)

$$\overline{W}{p}_4^{\prime }=p_4\lambda +rp(1-p)(Q-R){\vartheta }_{p,m}$$ (35d)

for the haplotype frequencies in consecutive generations, where W̄ = pλ + (1 − p)μ.

Moreover using (35) we arrive at

$$R^{\prime }=\frac{p_1^{\prime }}{p_1^{\prime }+p_2^{\prime }}=\frac{p_1\mu +rp(1-p)(Q-R){\vartheta }_{p,m}}{(1-p)\mu }=R+rp(Q-R)\frac{{\vartheta }_{p,m}}{\mu }$$

and

$$Q^{\prime }=\frac{p_3^{\prime }}{p_3^{\prime }+p_4^{\prime }}=\frac{p_3\lambda -rp(1-p)(Q-R){\vartheta }_{p,m}}{p\lambda }=Q-r(1-p)(Q-R)\frac{{\vartheta }_{p,m}}{\lambda }.$$

We further obtain

$$Q^{\prime }-R^{\prime }=(Q-R)\left(1-r{\vartheta }_{p,m}\left(\frac{1-p}{\lambda }+\frac{p}{\mu }\right)\right).$$

Let us denote the respective frequencies in generation t by Q_t, R_t, and p_t. By using (28) we arrive at

$$\begin{array}{l}{Q}_{t+1}-R_{t+1}=(Q_t-R_t)\left(1-r{\vartheta }_{p_t,m}\left(\frac{1-p_t}{\lambda }+\frac{p_t}{\mu }\right)\right)\\ =(Q_t-R_t)\left(1-r\frac{{\vartheta }_{p_t,m}}{\lambda \mu }\left(\frac{p_0{\lambda }^{t+1}+(1-p_0){\mu }^{t+1}}{p_0{\lambda }^t+(1-p_0){\mu }^t}\right)\right).\end{array}$$

Furthermore, we have

$${\vartheta }_{p_t,m}:={(p_0{\lambda }^t+(1-p_0){\mu }^t)}^{2-m}\sum _{k=0}^{m-2}\left(\begin{array}{c}m-2\\ k\end{array}\right){\theta }_{k,m}{p}_0^k{\lambda }^{tk}{(1-p_0)}^{m-k-2}{\mu }^{t(m-k-2)},$$

which simplifies to (12), and Λ_m,t as in (13).

Using this we obtain

$$Q_t-R_t=(Q_0-R_0)\prod _{l=0}^{t-1}{\mathrm{\Lambda }}_{m,l}.$$ (36)

Hence,

$$\begin{array}{l}{Q}_{t+1}=Q_t-r(1-p_t)(Q_t-R_t)\frac{{\vartheta }_{p_t,m}}{\lambda }\\ =Q_t-r(1-p_0)(Q_t-R_t)\frac{{\mu }^t{\vartheta }_{p_t,m}}{\lambda (p_0{\lambda }^t+(1-p_0){\mu }^t)}\\ =Q_t-r(1-p_0)(Q_0-R_0)\frac{{\mu }^t{\vartheta }_{p_t,m}}{\lambda (p_0{\lambda }^t+(1-p_0){\mu }^t)}\prod _{l=0}^{t-1}{\mathrm{\Lambda }}_{m,l}\\ =Q_t+r(R_0-Q_0)\frac{{\vartheta }_{p_t,m}}{\lambda (\frac{p_0}{1-p_0}{(\frac{\lambda }{\mu })}^t+1)}\prod _{l=0}^{t-1}{\mathrm{\Lambda }}_{m,l}\\ =Q_0+\frac{r(R_0-Q_0)}{\lambda }\sum _{\tau =0}^t\frac{{\vartheta }_{p_{\tau },m}}{\frac{p_0}{1-p_0}{(\frac{\lambda }{\mu })}^{\tau }+1}\prod _{l=0}^{\tau -1}{\mathrm{\Lambda }}_{m,l}.\end{array}$$

Hence, the expression (14) for Q_t follows immediately. Moreover, the expression (15) for R_t is derived similarly.