Scheme 2.

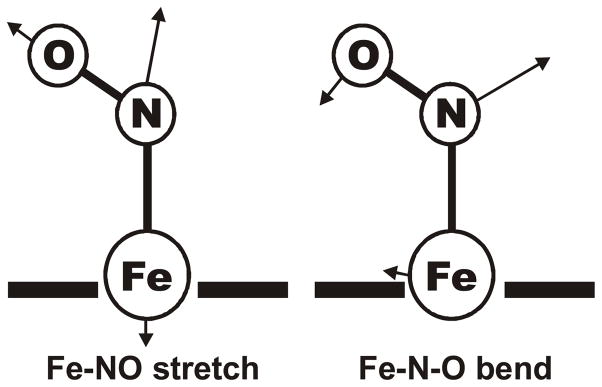
Effective internal coordinates for the Fe-NO stretch and the Fe-N-O bend in a [Fe(Porphyrin)] complex. These are taken from a BP86/TZVP calculation on [Fe(P)(NO)] where mixing of these internal coordinates is minimal. These effective internal coordinates are somewhat different from corresponding coordinates in a Fe-N-O trinuclear unit, because they account for intrinsic couplings of the isolated (pure) Fe-NO stretching and Fe-N-O bending coordinates of the triatomic with other internal coordinates in the actual complex. For example, in the bent Fe-N-O geometry, the Fe-N-O bending internal coordinate is always strongly mixed with (Pyr)N-Fe-N(O) octahedral bends (Pyr = pyrrole). Hence, the effective internal coordinates shown here are a better basis to understand the resulting Fe-NO stretching and Fe-N-O bending normal modes in complex 1. In comparison with Figure 7, one recognizes that the higher energy mode in 1 is always the ‘in-phase’ combination of these coordinates, whereas the lower energy mode is the corresponding out-of-phase combination, keeping in mind that (a) in the latter case, the contribution of the Fe-N-O bending internal coordinate is rather small, and (b) mixing with nearby porphyrin-based vibrations will influence the motions of the Fe-N-O unit.