Autonomic Neural Control of Cerebral Hemodynamics

Despite the rich innervation of the cerebral vasculature by both sympathetic and parasympathetic nerves [1], the role of autonomic control in cerebral circulation and, particularly, cerebral hemodynamics is not entirely clear [2]. Previous animal studies have reported inconsistent results regarding the effects of electrical stimulation or denervation on cerebral blood flow (CBF), cerebral pressure-flow relationship, and cerebral vessel response to metabolic stimuli [3]–[5]. Moreover, with the advance of transcranial Doppler ultrasound (TCD), which yields accurate-measurements of CBF velocity (CBFV) with high time resolution [6], it has been found that in humans CBFV in the middle cerebral artery decreased substantially during lower body negative pressure (LBNP) and head-up tilt in the absence of systemic hypotension, which suggests the presence of cerebral vasoconstriction associated with augmented sympathetic nerve activity during orthostatic stress [7]. These observations were based on assessing static measures of cerebral circulation, i.e., mean values of artevial blood pressure (ABP) and CBF with a low time resolution.

However, the dynamic nature of cerebral autoregulation has been revealed using TCD measurements, to examine both the CBFV response to experimentally induced ABP changes [8]–[10] and the dynamic relation between spontaneous beat-to-beat ABP and CBFV variations [11]–[14]. These latter studies have revealed that dynamic autoregulation during resting conditions is frequency dependent, with slow ABP changes being attenuated more effectively by the cerebrovascular bed [14]. In this context, autonomic control of dynamic cerebral autoregulation was studied more recently by examining the dynamic relation between beat-to-beat ABP and CBFV variations during autonomic ganglion blockade. Transfer function analysis revealed a significant increase in the gain between ABP and CBFV from 0.02 to 0.07 Hz, suggesting altered autoregulation and active autonomic control [15].

The cerebrovascular bed is exquisitely sensitive to changes in arterial CO₂ [1]. Recent studies have shown that small, spontaneous fluctuations of arterial CO₂ tension around the mean, assessed by end-tidal CO₂ (P_ETCO2) measurements, have a significant effect on slow fluctuations of both CBFV [12], [16] as well as regional blood flow, assessed by blood oxygen level-dependent functional magnetic resonance imaging [17], [18]. Furthermore, it has been suggested that cerebral hemodynamics are characterized by nonlinearities, both on the basis of low coherence values between ABP and mean CBFV (MCBFV) below 0.07 Hz [14] and by exploring the use of linear autoregressive models and the presence of nonlinear dynamics [19]. Consequently, we and others have shown that nonlinear Volterra models and/or multivariate models that incorporate P_ETCO2 variability are able to explain a considerably larger fraction of CBFV variability [12], [13], [16], [20], [21]. The effects of dynamic nonlinearities and CO₂ were found to be more pronounced in the low-frequency (LF) range (particularly below 0.04 Hz) [16], suggesting that the aforementioned low coherence arises from both these factors [16], [21] .

The present article examines the role of autonomic neural control on both dynamic pressure autoregulation and CO₂ reactivity in the frequency range between 0.005 and 0.40 Hz by analyzing experimental data from healthy humans and using a nonlinear multivariate modeling approach. The data were obtained during control conditions and autonomic ganglionic blockade, induced by intravenous infusion of trimethaphan. This approach has been successfully used previously to describe cerebral hemodynamics during resting conditions [16], [20] and orthostatic stress [22].

Methods

Experimental Methods

Twelve healthy subjects (nine men) with a mean age of 29 ± 6 years, height of 174 ± 10 cm, and weight of 71 ± 10 kg voluntarily participated in this study. No subject smoked or had known medical problems. All subjects signed an informed consent form approved by the Institutional Review Boards of the University of Texas Southwestern Medical Center and Presbyterian Hospital of Dallas. ABP was measured noninvasively with finger photoplethysmography (Finapres), while CBFV was measured continuously in the middle cerebral artery using a 2-MHz TCD probe. Heart rate was monitored by a 12-lead ECG. P_ETCO2 was obtained via a nasal cannula by using a mass spectrometer. The TCD probe was placed over the subject’s temporal window and fixed at a constant angle, with a probe holder that was custom-made to fit each subject’s facial bone structure.

All experiments were performed in the morning in a quiet, environmentally controlled laboratory. After at least 30 min of supine rest, 6 min of baseline data were collected during spontaneous breathing. Then the subjects performed a Valsalva maneuver with an expiratory strain of 30 mmHg for 15 s. After the baseline Valsalva maneuver, infusion of trimethaphan was performed at a low dose of 3 mg/min. Three minutes after the infusion, the Valsalva maneuver was repeated to evaluate both the heart rate and pressure responses. The infusion dose was increased incrementally by 1 mg/min, until the heart rate response during the Valsalva maneuver was eliminated.

The absence of heart rate response, plus the absence of phase II recovery, and phase IV overshoot of arterial pressure during the Valsalva maneuver demonstrated the efficacy of ganglion blockade on both parasympathetic and sympathetic nerve activity [23]. The ultimate infusion dose used for ganglion blockade was 6–7 mg/min for most subjects in the present study. Once complete blockade was achieved, the infusion of trimethaphan continued at this maximal dosage throughout the experiments. Six minutes of data were then collected after ganglion blockade. Finally, since the LF ABP variability after ganglion blockade was reduced, oscillatory LBNP with a magnitude of 0–5 mmHg at a frequency of 0.05 Hz was applied in ten subjects to simulate LF blood-pressure variability. Six minutes of data were collected under this condition as well.

Mathematical Methods

Beat-to-beat mean ABP (MABP) andMCBFV were obtained by integrating the obtained analog signals within each cardiac cycle. The beat-to-beat MABP and MCBFV data, as well as breath-by-breath P_ETCO2 data, were resampled at 1 Hz for subsequent analysis. Steady state and variability (standard deviations around mean value) values for MABP, MCBFV, and P_ETCO2 were calculated for each subject and group averaged during all experimental phases (baseline, ganglion blockade, and simultaneous blockade and LBNP). The power spectral density (PSD) of the signals was estimated by employing the Welch-modified periodogram method [24]. To quantify the spectral power of the hemodynamic signals within specific frequency bands of interest, we integrated the signal PSD over the very low- (VLF; 0.005– 0.04 Hz), low- (LF; 0.04–0.15 Hz), and high-frequency (HF) ranges (0.15–0.40 Hz), respectively. These limits were selected on the basis of frequency-domain characteristics of dynamic MABP-MCBFV and P_ETCO2 -MCBFV relationships, as determined by our previous studies [16].

The presence of nonlinearities in cerebral hemodynamics has been suggested in previous studies [12]–[14], [16], [19]. Therefore, we employed a two-input, general Volterra model of cerebral hemodynamics to quantitatively describe the dynamic effects of spontaneous MABP and P_ETCO2 changes on MCBFV variations [16]:

$$\text{MCBFV}(n)=k_0+{\displaystyle \sum _{i=1}^2{\displaystyle \sum _{m_1}{k}_{1x_i}(m_1)x_i(n-m_1)}}+{\displaystyle \sum _{i_1=1}^2{\displaystyle \sum _{i_2=1}^2\left\{{\displaystyle \sum _{m_1}{\displaystyle \sum _{m_2}{k}_{2x_{i_1}{x}_{i_2}}(m_1,m_2)x_{i_1}(n-m_1)x_{i_2}(n-m_2)}}\right\}+\cdots +{\displaystyle \sum _{i_1=1}^2\cdots {\displaystyle \sum _{i_Q=1}^2\left\{{\displaystyle \sum _{m_1}\cdots {\displaystyle \sum _{m_Q}{k}_{Q{x}_{i_1}\cdots x_{i_Q}}(m_{1,}\dots ,m_Q)\times x_{i_1}(n-m_1)\dots x_{i_Q}(n-m_Q)}}\right\},}}}}$$ (1)

where x_i: MABP, CO₂. The linear (Q = 1) and nonlinear (Q > 1) Volterra kernels (k_q) describe the linear and nonlinear effects of MABP and P_ETCO2 (as well as their nonlinear interactions) at time lags (m₁, …, m_q) before the present time lag n on MCBFV and are used to quantify dynamic pressure autoregulation and CO₂ reactivity, respectively. The Volterra kernels were estimated on the basis of MABP, P_ETCO2, and MCBFV data by employing the Laguerre-Volterra network (LVN) methodology [25], which combines Laguerre function expansions and networks with polynomial activation functions and has been shown to yield accurate models of nonlinear systems from short input–output records. According to this methodology, the two input signals are convolved with two distinct Laguerre filter banks, with impulse responses given by the discrete-time Laguerre functions of orders up to L₁ and L₂, respectively. The outputs of the two filter banks are fully connected to K hidden units with polynomial activation functions of order Q. The output of the LVN model is given by the sum of the hidden unit outputs and a constant term [25]. The Volterra kernels in (1) can be expressed in terms of the LVN parameters (i.e., the weights between the filter banks and the hidden units, the polynomial coefficients of the latter, the output constant term, and the parameters of the two filter banks determining the dynamic properties of the Laguerre functions), which are in turn estimated via an iterative gradient descent algorithm from the input–output data. Therefore, dynamic pressure autoregulation and dynamic CO₂ reactivity are described by the Volterra kernels k_{qxi … xi} for i = 1 and i = 2, respectively (q = 1, …, Q), in the convolutional terms of (1). Further details on the methodology are provided in [25].

Model estimation was performed by using 5-min data segments (300 points) for training and the remaining 1 min for validation purposes. The structural parameters of the LVN models (the number of Laguerre functions corresponding to the two inputs L₁ and L₂, respectively, the number of hidden units K, and the polynomial order Q) were selected by a multi-objective criterion, i.e., the combined normalized mean-square error (NMSE) of the output prediction that was achieved for the training and validation data sets. The NMSE is defined as the sum of squares of the model residuals (the difference between the model prediction and the true output) divided by the sum of squares of the demeaned true MCBFV output. The statistical significance of the reduction achieved in the prediction NMSE for a model structure of increased order/complexity was assessed by comparing the percentage NMSE reduction with the α-percentile value of a chi-square distribution with Δp degrees of freedom (where Δp is the increase of the number of free parameters of the more complex model and p is equal to (L₁ + L₂ + K + 2) ·Q + 3 for a given LVN structure) at a significance level α of 0.05 [26].

The first-order MABP and P_ETCO2 kernels (k_1MABP and k_1CO2) were computed in the time and frequency domains, by calculating the magnitude of their discrete Fourier transforms (DFT) f_1MABP and f_1CO2, respectively, and subsequently group averaged. The second-order MABP and P_ETCO2 self-kernels (k_2MABP and k_2CO2) were obtained in the frequency domain by calculating the magnitude of their two-dimensional (2-D) DFTs (f_2MABP and f_2CO2), respectively. The first- and second-order kernel spectral power was calculated by integrating f_1MABP and f_1CO2 within the VLF, LF, and HF ranges defined as earlier, as well as f_2MABP and f_2CO2 in the 2-D frequency domain (i.e., VLF: [0.005, 0.005] to [0.04, 0.04] Hz, LF: [0.04, 0.04] to [0.15, 0.15] Hz, and HF: [0.15, 0.15] to [0.40, 0.40] Hz), respectively.

Results

Hemodynamic Signals

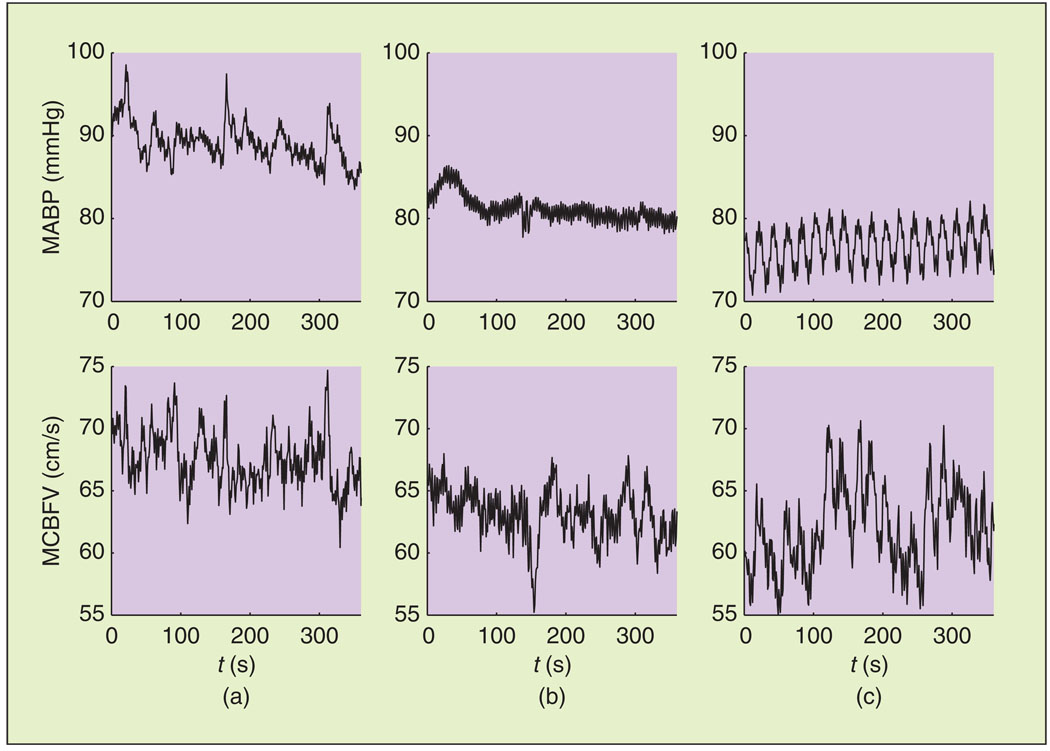
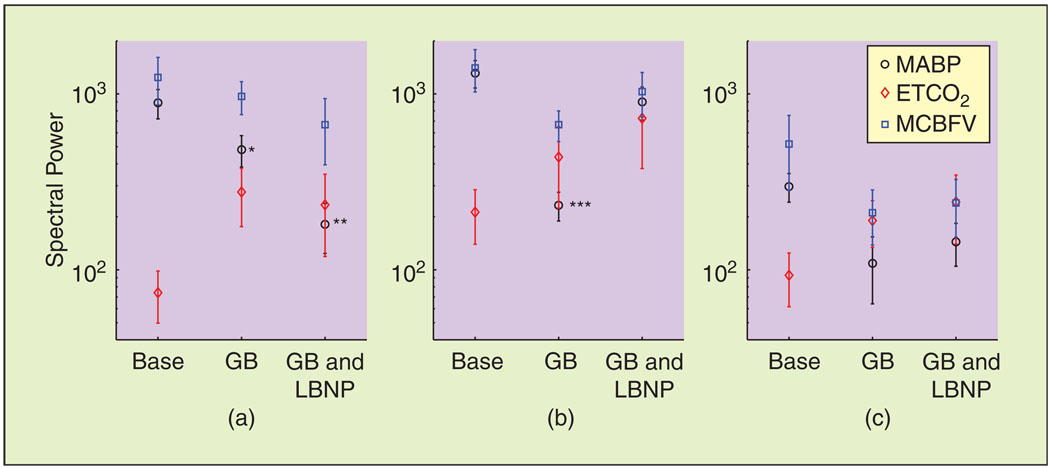
As reported previously [15], the steady-state values of MABP and MCBFV reduced during ganglion blockade, while the steady-state value of P_ETCO2 reduced to a smaller degree (Table 1). Representative data segments of MABP and MCBFV variations, used for model estimation, are shown in Figure 1. The mean values of MABP and MCBFV reduced during ganglion blockade. Moreover, trimethaphan infusion affected the dynamic characteristics of both signals, reducing their LF oscillations considerably [Figure 1(b)], while the application of LBNP restored some of this LF variability [Figure 1(c)]. This is further illustrated in Figure 2, where we show the spectral power in the VLF and LF ranges, averaged over all subjects. MABP power decreased markedly in the VLF (P < 0.01) and LF (P < 0.001) ranges. P_ETCO2 power exhibited an increasing trend in the VLF and LF ranges, while MCBFV power decreased, albeit less than its MABP counterpart (P = 0.09), in the LF range. In the HF range, no statistically significant differences were observed.

Table 1.

Steady-state hemodynamic parameters (mean ± SE).

	Baseline	Ganglion Blockade	Ganglion Blockade and LBNP
MABP (mmHg)	85.7 ± 2.4	79.4 ± 3.4	73.9 ± 4.5*
MCBFV (cm/s)	64.3 ± 4.4	60.2 ± 3.5**	58.11 ± 3.9*
PETCO2 (mmHg)	39.7 ± 0.8	37.0 ± 1.4	36.0 ± 1.6

^*P < 0.01,

^**P < 0.05 versus baseline.

Fig. 1.

Representative MABP and MCBFV time series used for model estimation. (a) Baseline. (b) Ganglion blockade. (c) Ganglion blockade and LBNP.

Fig. 2.

Hemodynamic signal spectral power in the (a) VLF (0.005–0.04 Hz), (b) LF (0.04– 0.15 Hz), and (c) HF (0.15–0.40 Hz) ranges. Note the decrease in the MABP signal power in both VLF and LF ranges induced by ganglion blockade, restored in the LF range by the application of LBNP. Base: baseline, GB: ganglion blockade, GB and LBNP: ganglion blockade and LBNP. *P < 0.05, **P < 0.01, ***P < 0.0001 compared to baseline.

Model Performance

The values of the LVN model structural parameters (i.e., number of Laguerre functions corresponding to the two inputs L₁ and L₂, number of hidden units K, and polynomial order Q) selected during each experimental condition are given in Table 2, averaged over all subjects. Nonlinear models (Q = 2 or 3) were shown to perform better than linear models, in terms of reducing the prediction error in a statistically significant manner according to the criterion described in the “Methods” section, in almost all cases (52 out of 54). The total number of 54 cases corresponds to 12 subjects during baseline and ganglion blockade and ten subjects during simultaneous ganglion blockade and LBNP. The number of hidden units (K) was selected equal to 3 in 53 out of 54 cases, while the optimal values of L₁, L₂ were found to lie between 7 and 9 in all cases. The NMSEs obtained for the selected models and the corresponding linear models in [Q = (1)—with all other structural parameters remaining the same], as well as NMSE reduction (ΔNMSE) obtained by the former, are also given in Table 2. Interestingly, the two cases where the nonlinear models did not satisfy the employed criterion occurred for the same subject (baseline and ganglion blockade). The averaged reduction in prediction NMSE achieved by nonlinear models ranged from 11.7% (from 18.8% to 7.1%; ganglion blockade and LBNP) to 19.1% (from 27.1% to 8.0%; ganglion blockade). The values of the structural parameters were robust among subjects and conditions, as the aforementioned optimal values lay within a narrow range of values.

Table 2.

The mean ± SE values of the LVN structural parameters and the output prediction NMSEs of the full and linear (Q = 1) models for the selected LVN models for each condition, averaged over all subjects.

Condition	L1, L2	K	Q	P	Full- Model NMSE (%)	Linear- Model NMSE (%)	ΔNMSE (%)
Baseline	8.6 ± 0.7	3 ± 0	2.4 ± 0.2	61.8 ± 0.8	7.1 ± 1.1	19.9 ± 3.0	12.8 ± 2.5
Ganglion blockade	8.4 ± 0.2	2.9 ± 0.1	2.5 ± 0.2	59.3 ± 1.9	8.0 ± 1.2	27.1 ± 4.8	19.1 ± 4.2
Ganglion blockade and LBNP	8.7 ± 0.2	3 ± 0	2.5 ± 0.2	62.7 ± 0.9	7.1 ± 0.9	18.8 ± 3.1	11.7 ± 2.7

The averaged NMSE reduction achieved by nonlinear models (Q = 2 or 3). ΔNMSE is also given in each case.

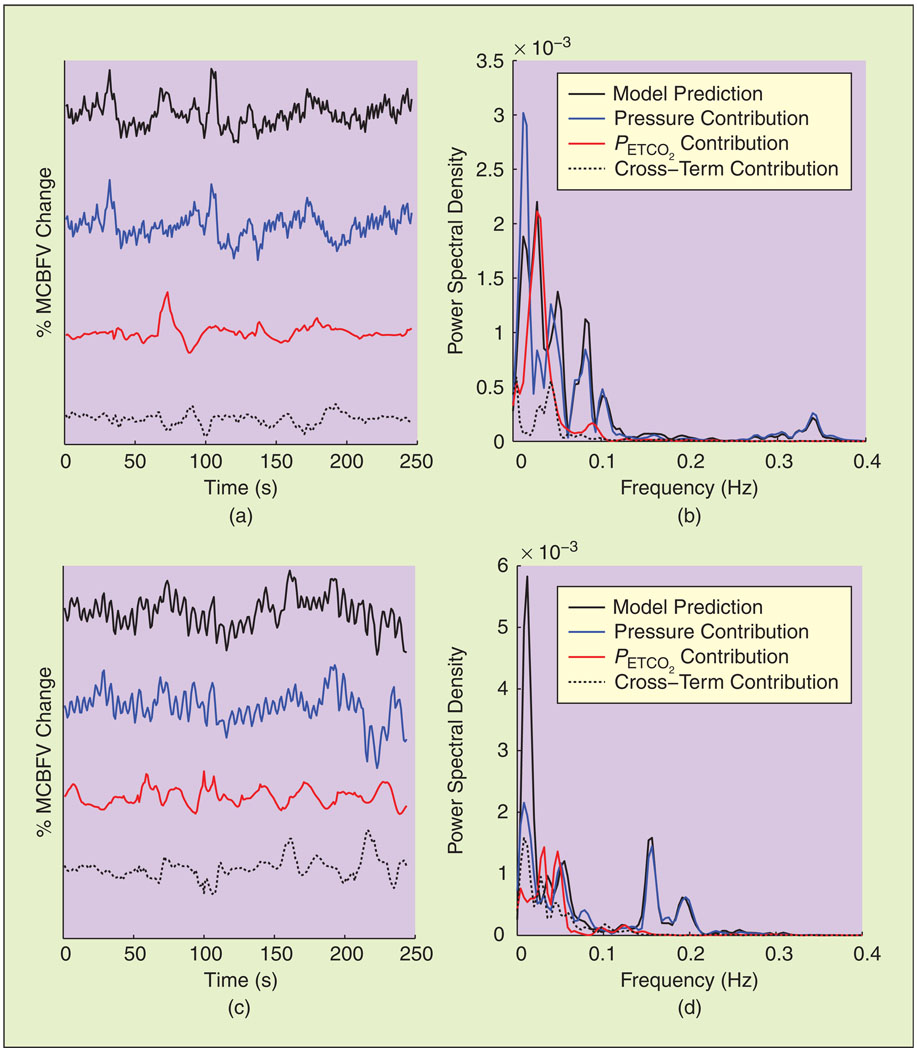
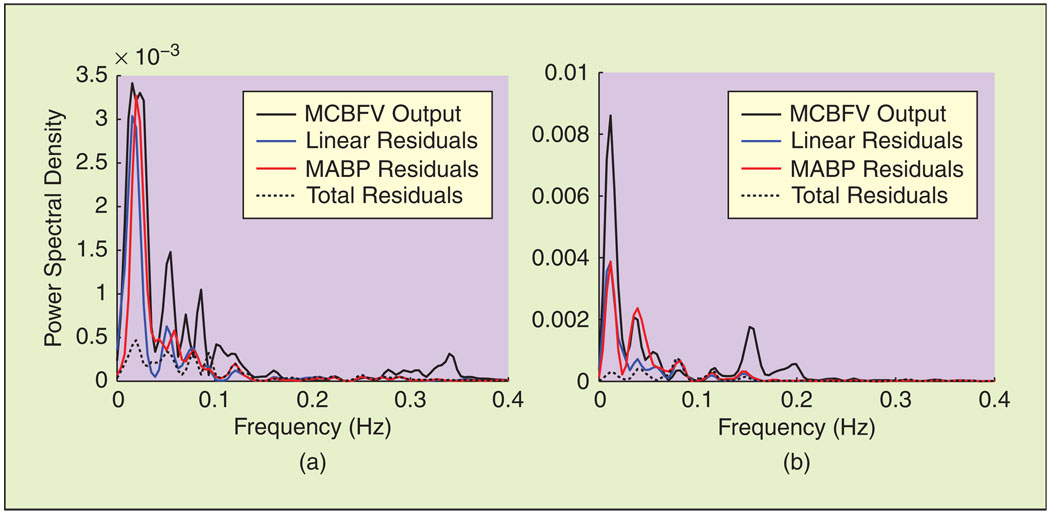
The contribution of the MABP, P_ETCO2, and cross terms in the time and frequency domains are shown in Figures 3 and 4 during baseline and ganglion blockade for a representative data segment. MABP explains most of the fast MCBFV variations, whileP_ETCO2 accounts for a significant fraction of the VLF MCBFV variations; note that its main contribution in the frequency domain, assessed by the difference between the PSD of the MABP and total model residuals lies below 0.04 Hz (Figure 4). Moreover, the contribution of the nonlinear model terms, assessed by the difference between the linear and nonlinear model residuals in the frequency domain, was more pronounced in the same range (Figure 4). These general characteristics were preserved during all experimental conditions, despite the aforementioned changes in the spectral characteristics of the hemodynamic signals (mainly MABP) induced by ganglion blockade. The spectral power of the model prediction and its decomposition in MABP, P_ETCO2, and cross-term components is given in Table 3, averaged over all subjects. No major differences were observed, except an increase in the HF power of the total model prediction and in the LF and HF power of its MABP component during simultaneous blockade and LBNP. The effect of P_ETCO2 was small in the HF range, while the LF power of the MABP component did not decrease, despite the decrease observed in MABP input power.

Fig. 3.

Decomposition of representative model prediction time series [(a) and (c), top traces] into its MABP and P_ETCO2 components in the time [(a) and (c)] and frequency [(b) and (d)] domains. (a) and (b) Baseline. (c) and (d) Ganglion blockade. Although MABP dominates in the HF range, P_ETCO2 accounts for a significant fraction of the VLF (below 0.04 Hz) MCBFV variability [(b) and (d)].

Fig. 4.

Spectral characteristics of model residuals for the time series of Figure 3. Most of the power of the linear model and MABP residuals resides in the VLF range, suggesting that the effects of nonlinearities and P_ETCO2 are more pronounced in this frequency range, both during (a) baseline and (b) ganglion blockade.

Table 3.

Spectral power of model prediction and its decomposition into MABP, P_ETCO2, and cross-term components (units are in % change), averaged over all subjects (mean ± SE).

	Baseline (×10−3)			Ganglion Blockade (×10−3)			Ganglion Blockade and LBNP (×10−3)
	VLF	LF	HF	VLF	LF	HF	VLF	LF	HF
Total   prediction	1.37 ± 0.38	0.72 ± 0.12	0.12 ± 0.03	1.34 ± 0.28	0.53 ± 0.11	0.23 ± 0.04	1.06 ± 0.21	1.48 ± 0.33	0.33* ± 0.05
MABP	0.97 ± 0.26	0.56 ± 0.07	0.11 ± 0.03	1.38 ± 0.57	0.58 ± 0.14	0.21 ± 0.04	2.12 ± 1.22	1.52* ± 0.34	0.33* ± 0.05
PETCO2	1.67 ± 0.65	0.60 ± 0.25	0.02 ± 0.01	1.23 ± 0.58	0.25 ± 0.06	0.01 ± 0.006	0.69 ± 0.21	0.42 ± 0.11	0.01 ± 0.002
Cross terms	1.17 ± 0.38	0.69 ± 0.31	0.02 ± 0.01	1.20 ± 0.36	0.52 ± 0.11	0.01 ± 0.003	1.55 ± 1.04	0.39 ± 0.08	0.02 ± 0.006

^*P < 0.05 versus baseline.

Spontaneous CO₂ variability has a pronounced effect on cerebral blood flow velocity in the very low frequency range.

Dynamic Pressure Autoregulation and CO₂ Reactivity

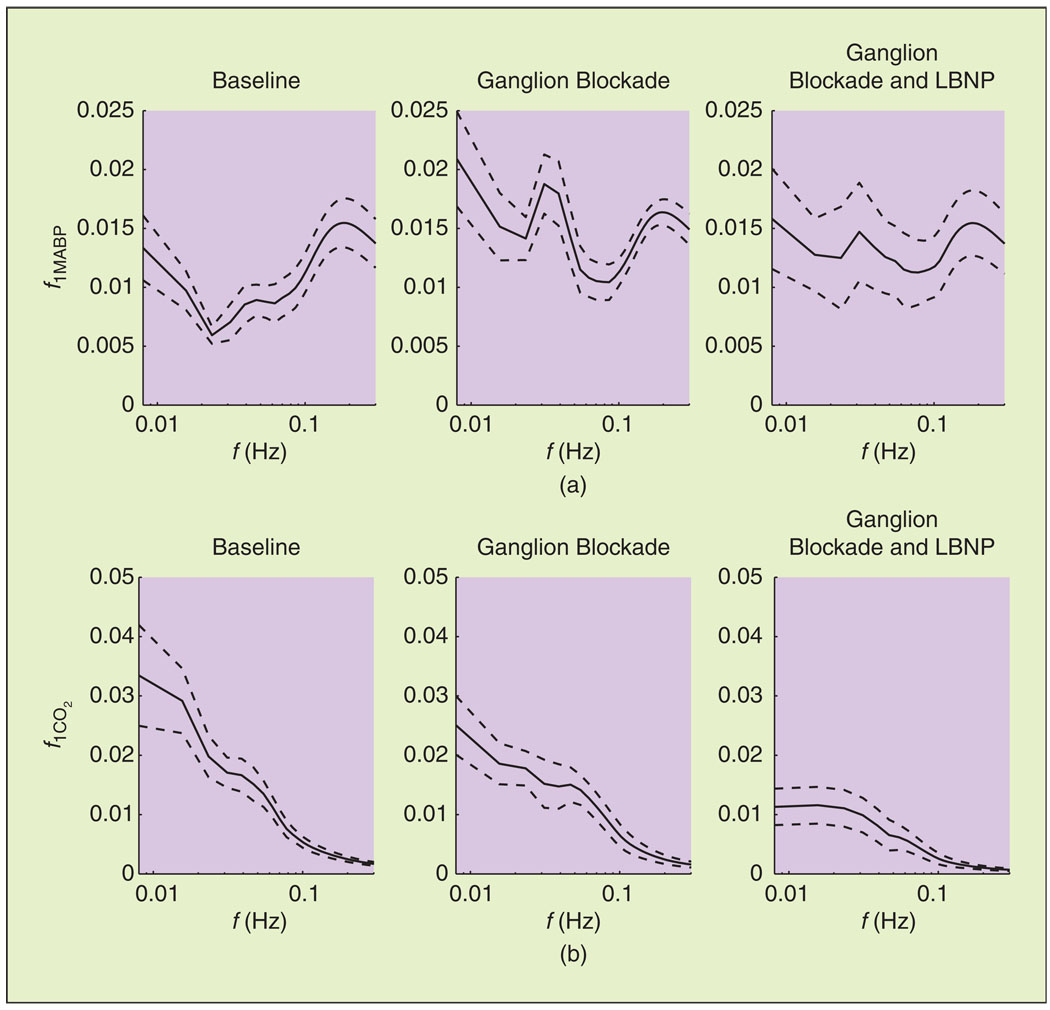
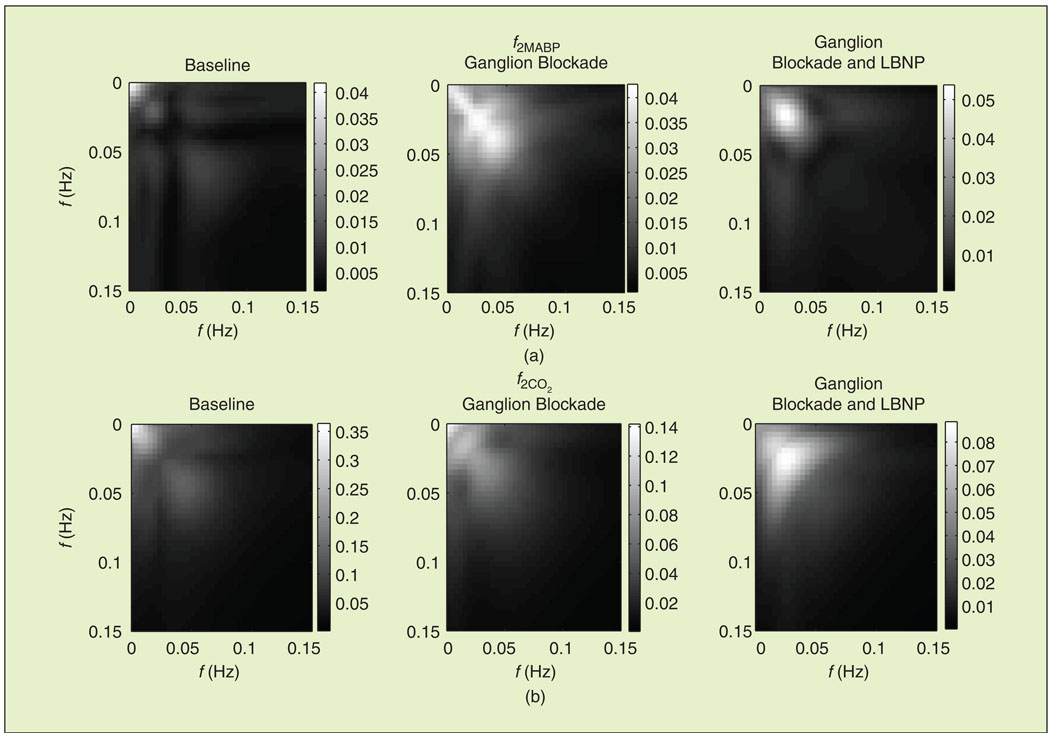
The magnitude of the first-order MABP kernel DFT f_1MABP, which corresponds to the linear component of dynamic pressure autoregulation, is shown in Figure 5, averaged over all subjects and during all three experimental conditions. Note that all kernels were estimated in units of % change in MCBFV per mm Hg. During baseline, f_1MABP resembled a high-pass characteristic that has been described in previous studies [12], [14], [16], which suggests that slow MABP oscillations are attenuated more efficiently. During ganglion blockade (both without and with simultaneous LBNP), f_1MABP was altered to a bandpass characteristic, and its values increased in the VLF and LF ranges [Figure 5(a)]. The form of the dynamic CO₂ reactivity linear component frequency response f_1CO2 did not change considerably, exhibiting a low-pass characteristic during all conditions [Figure 5(b)]. This suggests that slow CO₂ changes have a more pronounced effect on MCBFV variability. However, its values reduced during ganglion blockade. The 2-D DFT magnitude of the second-order autoregulation and CO₂ reactivity model components (f_2MABP and f_2CO2) are shown in Figure 6, averaged over all subjects. Most of their power resided below 0.15 Hz, and they were affected by trimethaphan similar to their first-order counterparts, i.e., the values of f_2MABP and f_2CO2 increased and decreased, respectively.

Fig. 5.

Linear component of (a) dynamic pressure autoregulation and (b) CO₂ reactivity in the frequency domain, averaged over all subjects (mean ± SE). The magnitude of f_1MABP in the VLF and LF ranges (below 0.15 Hz) increased during ganglion blockade.

Fig. 6.

Second-order component of (a) dynamic pressure autoregulation and (b) CO₂ reactivity in the frequency domain (2-D FFT), averaged over all subjects.

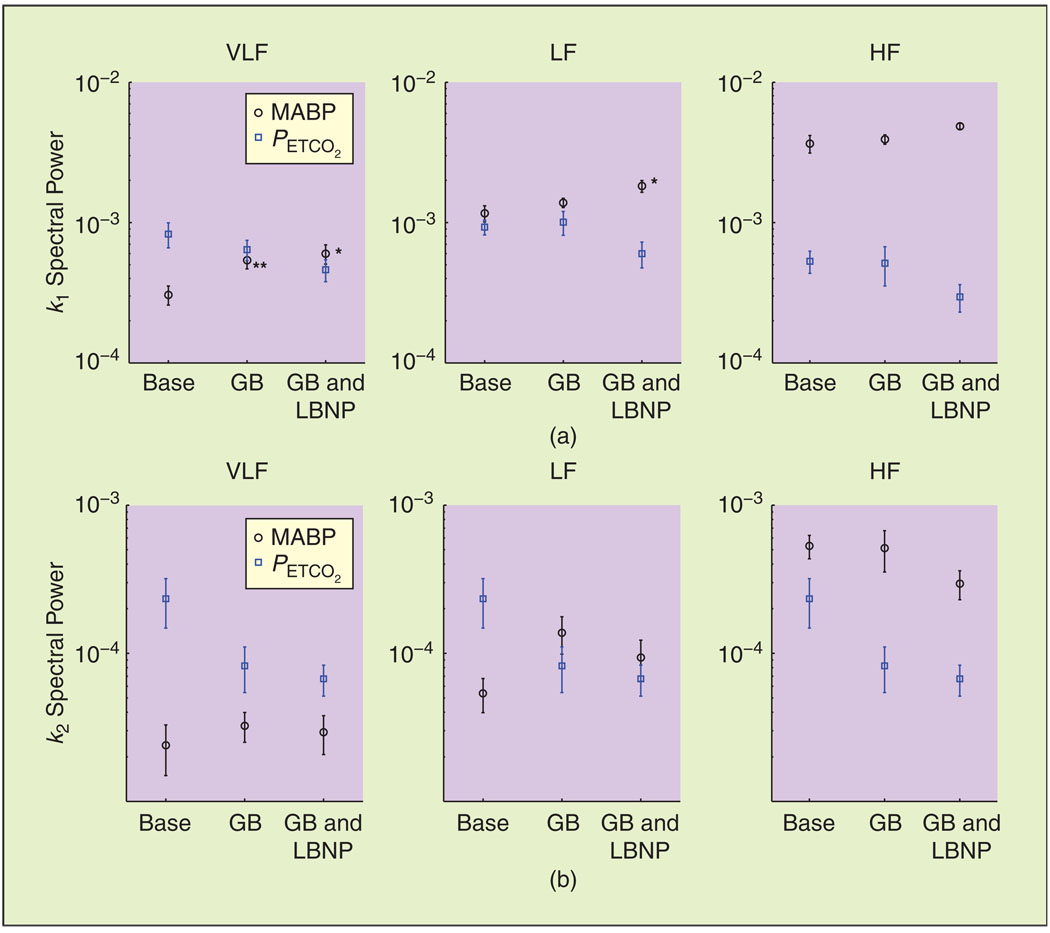
To further quantify the earlier observations, we show the spectral power of the first- and second-order model components, averaged over all subjects, in Figure 7(a) and (b), respectively. The spectral power of k_1MABP increased significantly in the VLF range (P < 0.01) during ganglion blockade and in the VLF and LF ranges (P < 0.05) during simultaneous blockade and LBNP [Figure 7(a)], in agreement with Figure 5.

Fig. 7.

Spectral power of the linear and nonlinear (a) dynamic pressure autoregulation [k_1MABP and k_2MABP] and (b) dynamic CO₂ reactivity [k_1CO2 and k_2CO2] model components (mean ± SE). Base: baseline, GB: ganglion blockade, GB and LBNP: ganglion blockade and LBNP. *P < 0.05, **P < 0.01.

On the other hand, despite the decrease observed in the values of f_1CO2 [Figure 5(b)], the differences in the k_1CO2 spectral power were not statistically significant (though marginally significant in some cases). This was mainly due to the variability of the individual estimates, which was more pronounced for the P_ETCO2 model terms. Finally, the second-order components exhibited similar trends to their first-order counterparts, with the differences being marginally significant in the LF range for the MABP and P_ETCO2 components (P = 0.08 and P = 0.06, respectively) between baseline and ganglion blockade (without LBNP).

Ganglionic blockade altered the high-pass characteristic of dynamic pressure autoregulation to a band-pass characteristic.

Discussion

We have examined the effects of autonomic blockade on cerebral hemodynamics in the entire frequency range between 0.005 and 0.40 Hz by analyzing experimental measurements of spontaneous MABP, P_ETCO2, and MCBFV variations with a nonlinear, two-input model, which assessed dynamic pressure autoregulation and CO₂ reactivity simultaneously. The main findings were as follows: 1) The characteristics of dynamic pressure autoregulation were altered considerably in the VLF and LF ranges (below 0.15 Hz), suggesting that slow MABP variations are not attenuated as effectively during ganglion blockade. This was observed during simultaneous LBNP as well, which restored some of the LF MABP variability that was abolished during blockade. 2) Reactivity to spontaneous CO₂ changes reduced during ganglion blockade; however, these differences were not as pronounced as for dynamic autoregulation. These findings extend previous observations regarding ganglion blockade-induced changes in the characteristics of the hemodynamic time series, i.e., a profound decrease in the MABP power between 0.02 and 0.07 Hz [15], [27], as well as an increase in the transfer function gain between MABP and MCBFV and a diminished phase lead of MCBFV in the same frequency range [15].

Spectral analysis provides information about the relative magnitude of different oscillatory patterns that are present in the hemodynamic time series (Figure 2); however, it does not provide any information about whether these patterns are correlated and at which frequencies. This information is provided by the estimated dynamic models (Figures 5– 7), which suggest that slow MABP changes are attenuated more effectively during baseline (high-pass characteristic, Figure 5). During ganglionic blockade, VLF and (particularly) LF MABP power reduced (Figure 2), but the spectral power of both the first- and secondorder MABP model components [k_1MABP and k_2MABP in (1)], which quantify dynamic pressure autoregulation, increased (Figure 7). As a result, the power of the MABP contribution did not decrease, and it accounted for a significant fraction of slow MCBFV variations (Table 3). On the other hand, the spectral power of P_ETCO2 increased during ganglionic blockade (Figure 2), but the power of the dynamic CO₂ reactivity model components decreased (Figure 7), so the net effect was a (nonsignificant) decrease in the power of the P_ETCO2 contribution (Table 3). Overall, the power of the MCBFV variability accounted by the model did not change during ganglion blockade (Table 3). Finally, the HF MCBFV power was predominantly accounted by MABP fluctuations (P_ETCO2 has a very small effect in this range, Table 3) and the linear and nonlinear dynamic autoregulation kernels were not affected (Figures 5 and 7, right panels).

The use of CBFV as an index for CBF has been discussed extensively [28], [29]. CBFV changes reflect CBF changes if the cross-sectional area of the insonated vessel remains relatively constant. It has been found that the diameter of the middle cerebral artery does not change in humans significantly during moderate LBNP (up to −40 mmHg) or during changes in P_ETCO2 [28], [29]. Therefore, we assumed that beat-to-beat MCBFV changes were a good index of beat-to-beat CBF changes.

Volterra-Wiener models have been employed extensively in the context of physiological systems [30]. This approach is well suited to the complexity of such systems, because it yields rigorous mathematical descriptions from input–output data, without requiring any a priori assumptions about system structure. The advantage of the LVN methodology is that it requires a substantially smaller number of free parameters compared with other techniques, such as cross-correlation or standard function expansions. Although this number depends exponentially on the system nonlinear order for alternative approaches, it depends linearly upon system order for the LVN approach [25]. For instance, in the case K = 3, which was selected in 53 of 54 cases, second- and third-order models (Q = 2, 3) required the estimation of only three and six additional free parameters compared with their linear counterparts. The performance of the obtained models was evaluated by using a multiobjective NMSE criterion instead of using only validation data, since cerebral hemodynamics are characterized by nonstationarities [16], [19]. By taking into account both in-sample and out-of-sample performance, we sought to avoid overfitting and biases because of possible nonstationarities in system dynamics. Note that we compared the results regarding model order obtained with the employed statistical criterion with the other statistical criteria used frequently, i.e., the Akaike and Bayesian information criteria (AIC and BIC), which yielded similar results. However, the ranges of parameter values were more robust for the employed χ₂ criterion. Moreover, this criterion was more conservative with respect to nonlinear models; according to the AIC and BIC, and in only one out of 54 cases were nonlinear models found not to perform better than linear models.

The fact that the observed changes were generally maintained during simultaneous ganglion blockade and LBNP suggests that they are not due to the pronounced changes in the spectral characteristics of the hemodynamic signals induced by trimethapan infusion (Figure 2), which could have affected the model estimates. Moreover, if either nonlinearities or CO₂ effects are not taken into account, the estimates of dynamic autoregulation and/or CO₂ reactivity may also be affected, particularly in the VLF range, where the effects of MABP and CO₂ are both pronounced and possibly correlated [16], [21]. Note that the effects of autonomic blockade below 0.02 Hz were not examined in a previous study utilizing the same experimental data [15], because of the low coherence between MABP and MCBFV in the VLF range. Our results generally agree with this latter study, which reported increased transfer function gain values between MABP and MCBFV and a diminished phase lead of MCBFV between 0.02 and 0.07 Hz. We have extended these observations by quantifying hemodynamics down to 0.005 Hz in a nonlinear context and obtaining estimates of dynamic CO₂ reactivity. In summary, our results suggest an active role of the autonomic nervous system in the dynamic regulation of CBF.

Biographies

Georgios D. Mitsis received his diploma in electrical and computer engineering from the National Technical University of Athens, Greece, in 1997, M.S. degrees in biomedical and electrical engineering from the University of Southern California, Los Angeles, California, in 2000 and 2001, respectively, and his Ph.D. degree in biomedical engineering from the University of Southern California in 2002. After postdoctoral appointments at the Biomedical Simulations Resource, Los Angeles, California, the Centre for Functional Magnetic Resonance Imaging of the Brain (fMRIB), University of Oxford, United Kingdom, and an ENTER Research Fellowship at the National Technical University of Athens, he joined the Department of Electrical and Computer Engineering, University of Cyprus, Nicosia, Cyprus, where he is currently a lecturer. His research interests include nonlinear and nonstationary systems identification, with applications to quantitative/systems biology and physiology, as well as functional magnetic resonance imaging of the brain.

Rong Zhang received his Ph.D. degree in aerospace physiology from the University of Fourth Military Medical University, China. He is currently an assistant professor in the Department of Internal Medicine, University of Texas Southwestern Medical Center, and director of Cerebrovascular Laboratory at the Institute for Exercise and Environmental Medicine at Texas Health Presbyterian Hospital, Dallas. His research interests are studying brain–blood flow regulation with aging in patients with hypertension and Alzheimer’s disease by using TCD and MRI. He has published seminal papers in dynamic cerebral autoregulation, and his current research is supported by the National Institute on Aging.

Benjamin D. Levine received his M.D. degree from Harvard University Medical School. He is a cardiologist and cardiovascular physiologist and is one of the world’s experts in the hemodynamics of orthostatic intolerance and syncope. He is the director of the Institute for Exercise and Environmental Medicine at Texas Health Presbyterian Hospital and a professor of medicine at the University of Texas Southwestern Medical Center. He is especially interested in the coupling between systemic circulation and cerebral circulation and, together with Dr. Rong Zhang, has designed sophisticated experiments to study cerebrovascular coupling before, during, and after spaceflight.

Efthalia Tzanalaridou received her B.S. degree in radiography and radiological technology from Technological Educational Institution of Athens in 1992 and her M.S. degree in health management from the University of Piraeus in 2009. She is currently the chief radiographer in the Interventional Cardiology and Electrophysiology Laboratory and Neuroradiology Laboratory at Athens Euroclinic, Athens, Greece.

Demosthenes G. Katritsisreceived his M.D. degree from the University of Athens Medical School in 1979 and his Ph.D. degree from the University of London in 1991. He is currently a director of the Department of Cardiology at Athens Euroclinic and a honorary consultant cardiologist at St. Thomas’ Hospital, London, United Kingdom. His research interests include the study of coronary circulation and myocardial infarction, evidence-based indications of coronary angioplasty, and ablation therapy of cardiac arrhythmias, especially atrial fibrillation. He has published more than 200 articles in international medical journals on most aspects of clinical and interventional cardiology and has coauthored several European and American textbooks of clinical cardiology.

Vasilis Z. Marmarelis received his diploma degree in electrical and mechanical engineering from the National Technical University of Athens, in 1972, and the M.S. and Ph.D. degrees in engineering science (information science and bioinformation systems) from California Institute of Technology, Pasadena, in 1973 and 1976, respectively. He joined the Faculty of Biomedical and Electrical Engineering at the University of Southern California, Los Angeles, where he is currently the professor and director of Biomedical Simulations Resource. He served as chair of the Biomedical Engineering Department from 1990 to 1996. His main research interests are in the areas of nonlinear and nonstationary system identification and modeling, with applications to biology, medicine, and engineering systems. He is the author of the book Nonlinear Dynamic Modeling of Physiological Systems and coauthor of Analysis of Physiological Systems: The White-Noise Approach and editor of three volumes of Advanced Methods of Physiological System Modeling. He has published more than 100 papers and book chapters in the area of system and signal analysis.