Figure 1. Schematic illustration of infection dynamics under gene therapy and of the development of resistance to it.
(A) Diagram of the baseline model, which considers only a single sensitive viral strain. Two types of T cells are considered: gene-modified cells which are protected from infection (shown in red) and non-modified cells that are susceptible to it (shown in blue). The proliferation rate of both cell populations is determined by a saturating function, 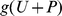 , which takes a Michaelis-Menten form. Therapy effects are conveyed via an infectivity inhibition factor (
, which takes a Michaelis-Menten form. Therapy effects are conveyed via an infectivity inhibition factor ( ) for gene-modified cells. (B) An example of a possible evolutionary path towards the emergence of a highly resistant strain. A genetic barrier
) for gene-modified cells. (B) An example of a possible evolutionary path towards the emergence of a highly resistant strain. A genetic barrier 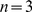 corresponds to a set of three resistance-conferring sites (hashes), where any combination of these sites can be mutated (stars). At each integration step of the simulation, a strain may only accrue a single mutation in one of the non-mutated sites. The degree of resistance is determined by the number of mutations (
corresponds to a set of three resistance-conferring sites (hashes), where any combination of these sites can be mutated (stars). At each integration step of the simulation, a strain may only accrue a single mutation in one of the non-mutated sites. The degree of resistance is determined by the number of mutations ( ), and is manifested as improved infection of P cells (i.e., higher infection rates due to an increase in
), and is manifested as improved infection of P cells (i.e., higher infection rates due to an increase in  ). Mutations are also associated with a loss in fitness that negatively affects the ability of these mutants to infect U cells, and that also depends on the number of mutations.
). Mutations are also associated with a loss in fitness that negatively affects the ability of these mutants to infect U cells, and that also depends on the number of mutations.

