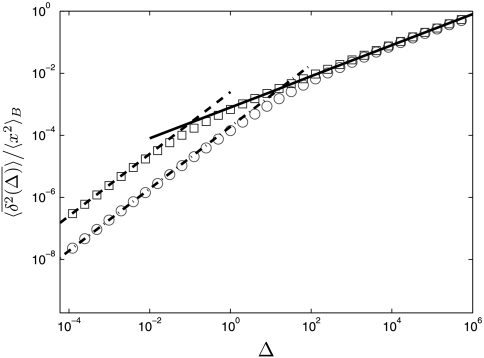
Fig. 2.

Simulated behavior of the time-averaged mean-squared displacement 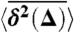for a continuous time random walk process with waiting time distribution ψ(t) ∼ τ^α/t^1+α, in an harmonic binding potential U(x) = x² (□), and in a box with reflecting boundary conditions and size 2 (○). The anomalous diffusion exponent is α = 1/2, and the measurement time was chosen as t = 10⁷ (a.u.). We also chose k_BT = 0.1, and K_1/2 = 0.0892. Without fit, the lines show the analytic results for the transition from the initial linear lag time dependence ≃Δ¹, 32 (−−− and − · −), to the long lag time behavior ≃Δ^1-α, 31 (—). In both cases 〈x〉_B = 0. At long lag times 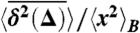exhibits universal behavior, independent of the external field.