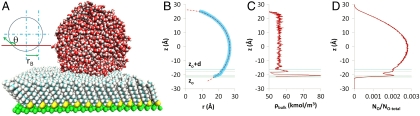
Fig. 4.

A set of figures to illustrate the calculation of contact angles. (A) A visual molecular dynamics visualization of a typical system setup. Here, using space-filling models, a water droplet is shown in contact with perfluorodecanethiol self-assembled monolayer (lattice spacing of 5.9 Å) after 3 ns of simulation time. Also shown is a sketch illustrating the meaning of contact angle (θ). (B) The profile of the liquid–vapor interface of the water droplet (about its center of mass averaged over 4,000 snapshots each 0.5 ps apart) is shown as shaded circles with the z position of a horizontal cross-section of the droplet plotted against the radius (r) of that cross-section. The broken line is the result of the points fitted to a circle. The lowermost solid horizontal line represents the height z_o at which represents the lowermost boundary of the water droplet. The uppermost solid horizontal line is the height (z_o + d) at which the water in the droplet can be said to have attained its bulk density. Hence we have two different ways of defining the contact angle. The broken horizontal lines in between represent the positions of the first and second peak in the density profile of water. (C) The profile of the density of water near the center of the droplet as a function of z position. It is structured at, and near, the solid–liquid interface but quickly attains its limiting value with increasing z. The horizontal lines are the same as for figure B. (D) The fraction of the number of O atoms in the droplet encountered in a z-direction slice 0.1-Å wide. The horizontal lines are the same as for figure B.