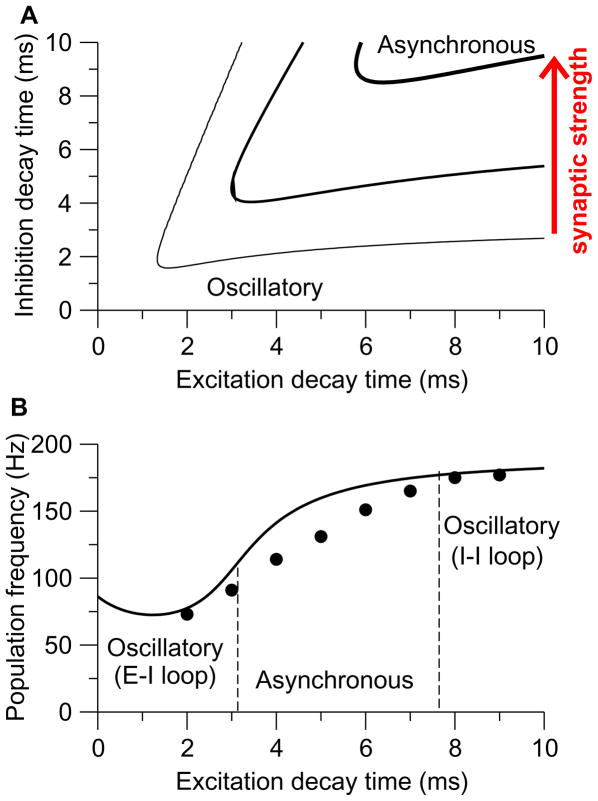
Figure 14. Dependence of sparsely synchronized oscillations on the strength and relative speeds of synaptic excitation and inhibition.

(A) Network dynamical behavior as a function of the excitatory (τ_E) and inhibitory (τ_I) synaptic time constants. A line separates the asynchronous state (upper right region) from the synchronous oscillation state (lower left region). This is shown with three levels of recurrent connection strength; coherent oscillations become more prevalent with stronger recurrence of the network. (B) population frequency as a function of the excitatory synaptic decay time constant τ_E, with fixed τ_I= 5 ms. Qualitatively, there are two kinds of instability from the asynchronous state to coherent oscillation. On one hand, when τ_E is much smaller than τ_I, the asynchronous dynamics is destabilized and oscillation develops through delayed inhibition in an excitatory-inhibitory loop scenario. On the other hand, when τ_E is sufficiently large, the excitatory drive is roughly tonic and the interneuronal network by itself generates synchronous oscillation. The oscillation frequency is much lower with shorter τ_E (gamma rhythm by the pyramid-interneuron loop mechanism) than with longer τ_E (ultrafast rhythm by the interneuronal network mechanism). Adapted with permission from [127].