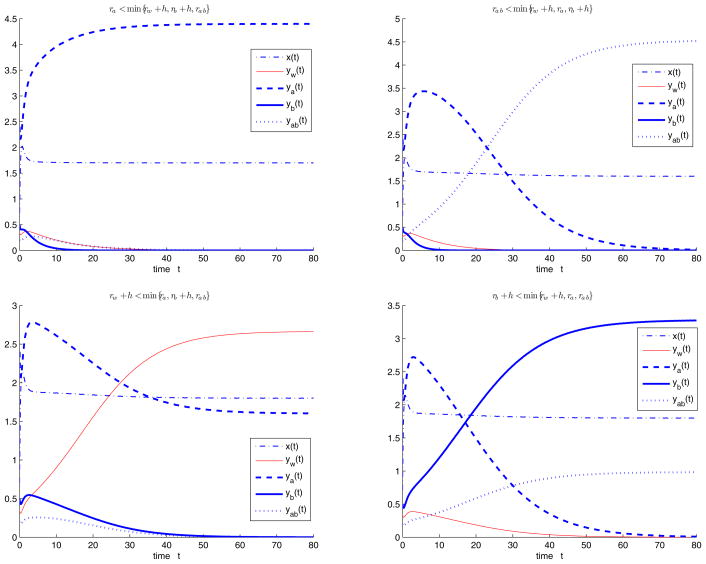
Figure 4.3.

System (1.2) with cycling treatment, i.e., when f_a = 1, f_b = f_ab = 0, we choose parameters Λ = 10, d = 2, b = 1, q = 0.1, s = 0.3, c = 1.5, h = 0.2, initial values x(0) = 0.65, y_w (0) = 0.35, y_a(0) = 2.4, y_b(0) = 0.5, y_ab(0) = 0.2, and let r_w, r_a, r_b, r_ab and h vary such that R₀ > 1. (i) When r_a < min{r_w + h, r_b + h, r_ab}, the semitrivial equilibrium E_a is stable; (ii) when r_ab < min{r_w + h, r_a, r_b + h}, the semitrivial equilibrium E_ab is stable; (iii) when r_w + h < min{r_a, r_b + h, r_ab}, the semitrivial equilibrium E_w,a is stable; (iv) when r_b + h < min{r_w + h, r_a, r_ab}, the semitrivial equilibrium E_b,ab is stable.