Experience Matters: Information Acquisition Optimizes Probability Gain

Abstract

Deciding which piece of information to acquire or attend to is fundamental to perception, categorization, medical diagnosis, and scientific inference. Four statistical theories of the value of information—information gain, Kullback-Liebler distance, probability gain (error minimization), and impact—are equally consistent with extant data on human information acquisition. Three experiments, designed via computer optimization to be maximally informative, tested which of these theories best describes human information search. Experiment 1, which used natural sampling and experience-based learning to convey environmental probabilities, found that probability gain explained subjects’ information search better than the other statistical theories or the probability-of-certainty heuristic. Experiments 1 and 2 found that subjects behaved differently when the standard method of verbally presented summary statistics (rather than experience-based learning) was used to convey environmental probabilities. Experiment 3 found that subjects’ preference for probability gain is robust, suggesting that the other models contribute little to subjects’ search behavior.

Many situations require careful selection of information. Appropriate medical tests can improve diagnosis and treatment. Carefully designed experiments can facilitate choosing between competing scientific theories. Visual perception requires careful selection of eye movements to informative parts of a visual scene. Intuitively, useful experiments are those for which plausible competing theories make the most contradictory predictions. A Bayesian optimal-experimental-design (OED) framework provides a mathematical scheme for calculating which query (experiment, medical test, or eye movement) is expected to be most useful. Mathematically, the OED framework is a special case of Bayesian decision theory (Savage, 1954). Note that a single theory is not tested in this framework; rather, multiple theories are tested simultaneously. The usefulness of an experiment is a function of the probabilities of the hypotheses under consideration, the explicit (and perhaps probabilistic) predictions that those hypotheses entail, and which informational utility function is being used.

When different queries cost different amounts, and different kinds of mistakes have different costs, people should use those cost constraints to determine the best queries to make, rather than using general-purpose criteria for the value of information. This article, however, addresses situations in which information gathering is the only goal. Specifically, we focus on situations in which the goal is to categorize an object by selecting useful features to view. Querying a feature, to obtain information about the probability of a stimulus belonging to a particular category, corresponds to an “experiment” in the OED framework and will generally change one’s belief about the probability that the stimulus belongs to each of several categories. For instance, in environments where a higher proportion of men than women have beards, learning that a particular individual has a beard increases the probability that he or she is male.

The various OED models differ in terms of how they calculate the usefulness of looking at particular features. All of the models use Bayes’s theorem to update the probability of each category (c_i) when a particular feature value f is observed:

$$P(c_i|f)=\frac{P(f|c_i)P(c_i)}{P(f)},$$ (1)

where

$$P(f)={\displaystyle \sum _{i}P(f|c_i)P(c_i)}$$

For updating to be possible, the probability distribution of the features and categories must be known. Conveying a particular set of environmental probabilities to subjects presents a practical difficulty, an issue we address subsequently.

Several researchers have offered specific OED models (utility functions) for quantifying experiments’ usefulness in probabilistic environments (e.g., Fedorov, 1972; Good, 1950; Lindley, 1956). We describe some prominent OED models from the literature in the next section. They disagree with each other in important statistical environments as to which potential experiment is expected to be most useful (Nelson, 2005, 2008).

OED Models of the Usefulness of Experiments

We use F (a random variable) to represent the experiment of looking at feature F before its specific form (f_j) is known. Each OED model quantifies F’s expected usefulness as the average of the usefulness of the possible f_j, weighted according to their probability:

$$E_{P(f)}[u(f)]={\displaystyle \sum _{j}P(f_j)u(f_j)},$$

where u(f_j) is the usefulness (utility) of observing f_j, according to a particular utility function. How does each OED model calculate of the usefulness of observing a particular feature value f_j, that is, u(f_j)?

Probability gain (PG; error minimization; Baron, 1981, cited in Baron, 1985) defines a datum’s usefulness as the extent to which it increases the probability of correctly guessing the category of a randomly selected item:

$$u_{\mathit{\text{PG}}}(f)=\underset{i}{\mathit{\text{max}}}(P(c_i|f))-\underset{i}{\mathit{\text{max}}}(P(c_i))$$

Probability gain is by definition optimal when correct decisions are equally rewarded and incorrect decisions are equally penalized (e.g., when each correct classification is worth a euro, and each incorrect classification is worth nothing).

Information gain (IG; Lindley, 1956) defines a datum’s usefulness as the extent to which it reduces uncertainty (Shannon entropy) about the probabilities of the individual categories c_i:

$$u_{\mathit{\text{IG}}}(f)={\displaystyle \sum _{i}P(c_i)\text{log}\frac{1}{P(c_i)}}-{\displaystyle \sum _{i}P(c_i|f)\text{log}\frac{1}{P(c_i|f)}}$$

Kullback-Liebler (KL) distance defines a datum’s usefulness as the extent to which it changes beliefs about the possible categories, c_i, where belief change is measured with KL (Kullback & Liebler, 1951) distance:

$$u_{\mathit{\text{KL}}}(f)={\displaystyle \sum _{i}P(c_i|f)\text{log}\frac{P(c_i|f)}{P(c_i)}}$$

Expected KL distance and expected information gain are always identical (Oaksford & Chater, 1996)—meaning E_P(f)[u_KL(f)] = E_P(f)[u_IG(f)]—making those measures equivalent for the purposes of this article.

Impact (Imp; Klayman & Ha, 1987, pp. 219–220; Nelson, 2005, 2008; Wells & Lindsay, 1980) defines a datum’s usefulness as the sum absolute change from prior to posterior beliefs (perhaps multiplied by a positive constant) over all categories:

$$u_{\mathit{\text{Imp}}}(f)={\displaystyle \sum _i|(P(c_i)-P(c_i|f))|}$$

Impact and probability gain are equivalent if prior probabilities of the categories are equal.

These utility functions can be viewed as candidate descriptive models of attention for categorization.

Bayesian diagnosticity (Good, 1950) and log diagnosticity, two additional measures, appear to contradict subjects’ behavior (Nelson, 2005), so we do not consider them here.¹

Statistical Models and Human Information Acquisition

Which, if any, of these OED models describe human behavior? Wason’s research in the 1960s and several subsequent articles suggest that there are biases in human information acquisition (Baron, Beattie, & Hershey, 1988; Klayman, 1995; Nickerson, 1998; Wason, 1960, 1966; Wason & Johnson-Laird, 1972; but see Peterson & Beach, 1967, pp. 37–38). Since about 1980, however, several authors have suggested that OED principles provide a good account of human information acquisition (McKenzie, 2004; Nelson, 2005, 2008; Trope & Bassok, 1982), even on Wason’s original tasks (Ginzburg & Sejnowski, 1996; McKenzie, 2004; Nelson, Tenenbaum, & Movellan, 2001; Oaksford & Chater, 1994). OED principles have been used to design experiments on human memory (Cavagnaro, Myung, Pitt, & Kujala, 2010), to explain eye movements as perceptual experiments (Butko & Movellan, 2008; Nelson & Cottrell, 2007; Rehder & Hoffman, 2005), to control eye movements in oculomotor robots (Denzler & Brown, 2002), and to predict individual neurons’ responses (Nakamura, 2006).

Some researchers have claimed that human information acquisition is suboptimal because it follows heuristic strategies. Those claims are questionable because certain heuristic strategies themselves correspond to OED models. Consider the feature-difference heuristic (Slowiaczek, Klayman, Sherman, & Skov, 1992). This heuristic, which applies in categorization tasks with two categories (c₁ and c₂) and two-valued features, entails looking at the feature for which |P(f₁|c₁) − P(f₁|c₂)| is maximized. This heuristic exactly implements impact, an OED model, irrespective of the prior probabilities of c₁ and c₂, and irrespective of the specific feature likelihoods (for proof, see Nelson, 2005, footnote 2; Nelson, 2009). This heuristic, therefore, is not suboptimal at all. In another case, Baron et al. (1988) found that subjects exhibited information bias—valuing queries that change beliefs but do not improve probability of a correct guess—on a medical-diagnosis information-acquisition task. Yet the OED models of information gain and impact also exhibit information bias (Nelson, 2005), which suggests that the choice of model may be central to whether or not a bias is found.

Which OED model best describes people’s choices about which questions to ask prior to categorizing an object? Nelson (2005) found that existing experimental data in the literature were unable to distinguish between the candidate models. Nelson’s new experimental results strongly contradicted Bayesian diagnosticity and log diagnosticity, but were unable to differentiate between other OED models as descriptions of human behavior.

In this article, we address whether information gain (or KL distance), impact, or probability gain best explains subjects’ evidence-acquisition behavior. We also test the possibility that people use a non-OED heuristic strategy of maximizing the probability of learning the true hypothesis (or category) with certainty (Baron et al., 1988). Mathematically, the probability-of-certainty heuristic states that a datum (e.g., a specific observed feature value or other experiment outcome) has a utility of 1 if it reveals the true category with certainty, and a utility of 0 otherwise.

We used computer search techniques to find statistical environments in which two models maximally disagree about which of two features is more useful for categorization and then tested those environments with human subjects. A major limitation of most previous work in this area is that the subjects have been told probabilities verbally. However, verbal description and experience-based learning result in different behavior on several psychological tasks (Hertwig, Barron, Weber, & Erev, 2004; McKenzie, 2006). We therefore designed an experiment using experience-based learning, with natural sampling (i.e., items were chosen at random from the specified environmental probabilities) and immediate feedback to convey the underlying probabilities. We also used a within-subjects manipulation to determine whether experience in the statistical environment and verbal statistics-based transmission of the same probabilities yield similar patterns of information acquisition.

Experiment 1: Pitting OED Theories Against One Another Using Experience-Based Learning

This experiment involved classifying the species of simulated plankton (copepod) specimens as species a or b (here, a and b play the role of c₁ and c₂), where the species was a probabilistic function of two two-valued features, F and G. Subjects first learned environmental probabilities in a learning phase, during which both features were visible, and then completed an information-acquisition phase, in which only one of the features could be selected and viewed on each trial.

In the learning phase, subjects learned the underlying environmental probabilities by classifying the species of each plankton specimen and were given immediate feedback. On each trial, a stimulus was chosen randomly according to the probabilities governing categories and features. One form of each feature was always present. The learning phase continued until a subject mastered the underlying probabilities. Figure 1 shows examples of the plankton stimuli and illustrates the probabilistic nature of the categorization task.

Fig. 1.

Illustrative plankton specimens. The plankton in the left half of the figure belong to species a, and those in the right half of the figure belong to species b. Note that only the eye (which can be yellow or black) and claw (which can be dark or light green) vary across the specimens. (See Figs. S1–S3 in the Supplemental Material available online for the actual stimuli; these examples have been altered to make the differences between features clearer in print.) Because of the probabilistic distribution of the features within each species, most specimens cannot be identified as species a or species b with certainty (i.e., the combination of black eye and light claw occurs in both categories). Assuming the observed specimens match underlying probabilities, the probabilities are as follows: P(species a|yellow eye) = 1, P(species b|black eye) = 8/13, P(species a|light-green claw) = 7/8, and P(species b|dark-green claw) = 7/8. Information gain, impact, and probability gain agree that the claw is more useful for categorizing a random specimen than the eye is, but only the eye offers the possibility of certainty.

In the subsequent information-acquisition phase, subjects continued to classify the plankton specimens. However, the features were obscured so that only one feature (selected by the subject) could be viewed on each trial. The feature likelihoods in each condition were designed so that two competing theories of the value of information strongly disagreed about which of the two features was more useful. In this way, subjects’ choice of which feature to view provided information about which theoretical model best described their intuitions about the usefulness of information. We pitted the different OED models and the probability-of-certainty heuristic against each other in four conditions, as shown in Table 1.

Table 1.

Feature Likelihoods to Best Differentiate Competing Theoretical Models of the Value of Information

	Feature likelihoods					Model preferring F (m1)				Model preferring G (m2)
Condition	P(f1|a)	P(f1|b)	P(g1|a)	P(g1|b)	DStr	Model	PStrm1	eum1(F)	eum1(G)	Model	PStrm2	eum2(F)	eum2(G)
1	0	.24	.57	0	14.5	Probability gain	14.4	0.072	0.000	Information   gain (impact,   probability   certainty)	−14.5	0.135	0.280
2	0	.29	.57	0	20.2	Probability gain	17.4	0.087	0.000	Impact   (information   gain,   probability   certainty)	−23.5	0.122	0.239
3	0	.40	.73	.22	8.2	Information gain   (probability   gain, probability   certainty)	7.2	0.238	0.166	Impact	−9.2	0.168	0.214
4	.05	.95	.57	0	37.9	Probability gain,   information   gain, impact	36.0a	—	—	Probability   certainty	−39.9	0.000	0.399

Note: Subjects classified the species of simulated plankton specimens as species a or b, where the species was a probabilistic function of two two-valued features, F (with values f₁ and f₂) and G (with values g₁ and g₂). In all conditions, P(a) = .70 and P(b) = .30. F denotes the feature with higher probability gain, and G denotes the feature with lower probability gain. Disagreement strength (DStr) is the geometric mean of the opposed models’ respective absolute preference strengths; it scales between 0 (none) and 100 (maximal). PStr_m1 denotes Model 1’s preference strength between F and G. This is positive because Model 1 prefers F over G in each case. PStr_m2 denotes Model 2’s preference strength between F and G. This is negative because Model 2 prefers G over F in each case. PStr scales between −100 and 100. The expected utility (eu) of F according to Model 1 is denoted by eu_m1(F). Models in parentheses were not optimized in the condition per se, but also prefer the feature in their respective columns.

^aIn Condition 4, PStr_m1 is based on the geometric mean of the individual preference strengths of probability gain (50), information gain (34), and impact (28).

Finally, each subject completed a verbal summary-statistic-based questionnaire on the usefulness of several features in an alien-categorization task. The questionnaire employed the same probabilities that the subject had just learned experientially on the plankton task. Inclusion of this questionnaire enabled within-subjects comparison of how the different means of conveying environmental probabilities affect information-acquisition behavior.

Subjects

Subjects were 129 students in social science classes at the University of California, San Diego. They received partial or extra course credit for participation. Subjects completed the study, which took 1.5 to 2 hr, in small groups of up to 5 people. They were assigned at random to one of the four conditions in Table 1, with the constraint of keeping approximately equal numbers of subjects who reached criterion learning-phase performance in each condition.

Optimizing experimental probabilities

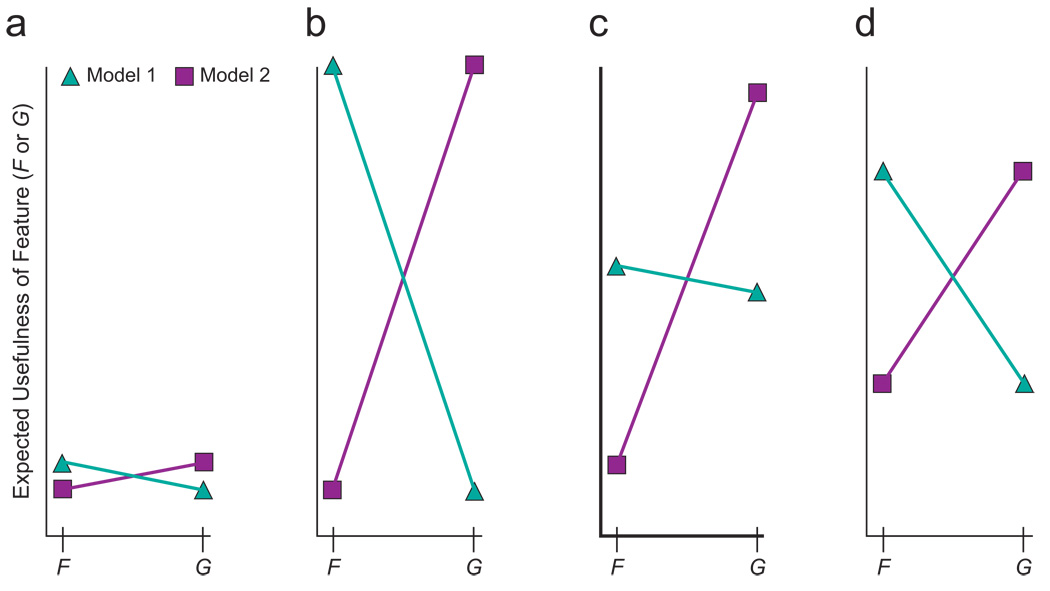
For each condition, we used computational search techniques to determine the feature likelihoods that would maximize disagreement between a pair of theories about which feature (F or G) was more useful for categorization (see Optimization Notes in the Supplemental Material available online for additional information on how the optimizations were conducted). This automatic procedure found scenarios with strong (and often nonobvious) disagreement between theories. Note that a prior probability distribution in this task is specified by five numbers: the prior probability of category a, or P(a), and four feature likelihoods, P(f₁|a), P(f₁|b), P(g₁|a), and P(g₁|b). We set P(a) to 70%, as suggested by Nelson’s (2005) optimizations. The program first found, at random, a case in which the two models disagreed, and then modified the four feature likelihoods to make that disagreement as large as possible (Fig. 2). Table 1 gives the feature likelihoods obtained by the optimization for each condition.

Fig. 2.

Four scenarios illustrating finding maximally informative features (F and G) to differentiate the predictions of competing theoretical models of the value of information (Model 1 and Model 2). The goal of optimization is to maximize disagreement strength (DStr)—which is based on the geometric mean of the two models’ absolute preference strengths—between the models. Because the optimization process generates feature likelihoods at random, the first step typically finds only weak disagreement between competing theoretical models of the value of information. In (a), Model 1 considers F to be slightly more useful than G, and Model 2 considers G to be slightly more useful than F. The shallow slopes of the connecting lines illustrate that the models’ (contradictory) preferences are weak, and DStr is low. An ideal scenario for experimental test is shown in (b). Model 1 holds that F is much more useful than G, whereas Model 2 has opposite and equally strong preferences. Thus, DStr is maximal. In (c), Model 2 strongly prefers G to F, and Model 1 marginally prefers F to G. This is not an ideal case to test experimentally. Because Model 1 is close to indifferent, DStr is low even though Model 2 has a strong preference. DStr is higher in (d) than in (c) because the models both have moderate (and contradictory) preferences.

We defined the preference strength of a model m for feature F(PStr_m) as the difference between the two features’ expected usefulness, eu_m(F) − eu_m(G), where each term is defined by Equation 1, scaled by the maximum possible difference in features’ usefulness according to model m (maxPStr_m) and multiplied by 100:

$${\mathit{\text{PStr}}}_m=100({\mathit{\text{eu}}}_m(F)-{\mathit{\text{eu}}}_m(G))/{\mathit{\text{maxPStr}}}_m$$

For all the OED models and the probability-of-certainty heuristic, the (typically unique) maxPStr_m is obtained when the categories are equally probable a priori, such that one feature is definitive, and the other feature is useless, for example, when P(a) = P(b) = .50, P(f₁|a) = 0, P(f₁|b) = 1, and P(g₁|a) = P(g₁|b).

We then defined the pair-wise disagreement strength (DStr) as the geometric mean of the opposed models’ respective absolute preference strengths (PStr_m1 and PStr_m2), when Model 1 and Model 2 disagree:

$${\mathit{\text{DStr}}}_{m1\mathit{\text{vs}}.m2}={(|{\mathit{\text{PStr}}}_{m1}|\times |{\mathit{\text{PStr}}}_{m2}|)}^{0.5},\text{if}{\mathit{\text{PStr}}}_{m1}\times {\mathit{\text{PStr}}}_{m2}\le 0$$

If, however, the models agree about which feature is most useful, DStr is zero:

$${\mathit{\text{DStr}}}_{m1\text{vs}.m2}=0,\text{if}{\mathit{\text{PStr}}}_{m1}\times {\mathit{\text{PStr}}}_{m2}\ge 0$$

An example calculation is provided in the Optimization Notes section of the Supplemental Material.

Experience-based learning experiment

Software was programmed to conduct the experiment. Subjects were familiarized with the features in advance, to ensure that they perceived the two variants of each feature (see Fig. S1 in the Supplemental Material for a sample stimulus from the learning phase). The physical features (eye, claw, and tail) were adjusted during pilot research to minimize any salience differences. Each subject was randomly assigned to one of 96 possible randomizations of each condition to guard against any residual bias among the physical features, the two variants of each feature, or the species names.

Design and procedure

The learning phase of the experiment was similar to the learning phase of probabilistic category-learning experiments (Knowlton, Squire, & Gluck, 1994; Kruschke & Johansen, 1999). In each trial, a plankton stimulus was randomly sampled from the environmental probabilities and presented to the subject: The category was chosen according to the prior probabilities P(a) and P(b), and the features were generated according to the feature likelihoods P(f₁|a), P(f₁|b), P(g₁|a), and P(g₁|b). There were no symmetries or other class-conditional feature dependencies. The subject classified the specimen as species a or b and was given immediate feedback (smiley or frowny face) on whether the classification was correct according to which category had been generated. Note that the optimal decision (corresponding to the category with highest posterior probability, given the observed features) was frequently given negative feedback, because certain combinations of features were observed in both species (cf. Fig. 1). Subjects were also given the running percentage of trials in which their classifications were correct.

Pilot work had revealed that subjects vary by more than a factor of 10 in the number of trials they need to learn environmental probabilities. Therefore, the learning phase continued until criterion performance was reached or the available time (~2 hr) elapsed. Criterion performance was defined as either making at least 99% optimal (not necessarily correct) responses in the last 200 trials, irrespective of the specific stimuli in those trials, or making at least 95% optimal responses in the last 20 trials of every single stimulus type. The goal was to ensure that subjects achieved high mastery of the environmental probabilities before beginning the information-acquisition (test) phase.² The test phase was designed to identify which of the two features the subject considered most useful and, by implication, which of the underlying theoretical models best describes the subjective value of information to that subject. The test phase consisted of 101 trials in which the features were initially obscured, and the subject could view only a single feature, chosen via a mouse click.

Results

The median number of trials required to achieve criterion performance in the learning phase was 933, 734, 1,082, and 690 trials in Conditions 1 through 4, respectively. Among the 129 subjects, 113 achieved criterion performance and were given the information-acquisition task.

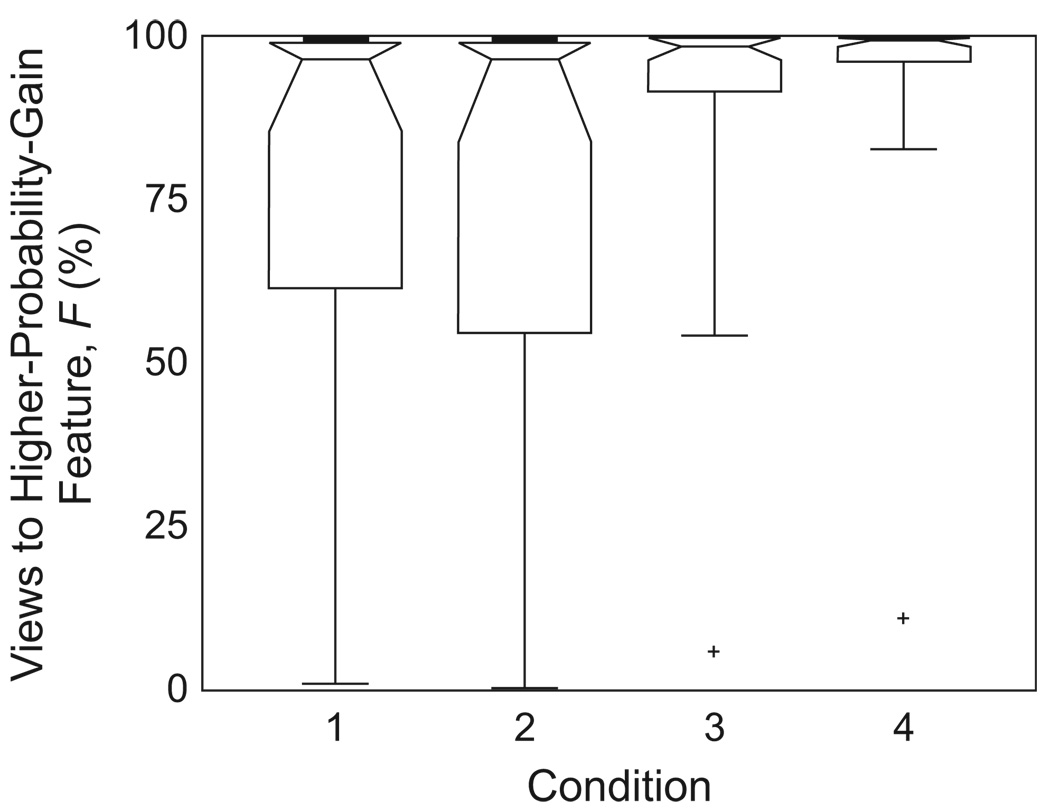
The most striking result from the information-acquisition task was that in all conditions, irrespective of which theoretical models were being compared, the feature with higher probability gain was preferred by a majority of subjects (Fig. 3). Moreover, the preference to view the feature with higher probability gain (F) was quite strong. Across all conditions, the median subject viewed the higher-probability-gain feature 99% of the time (in 100 of 101 trials).³ The median subject viewed F 97%, 97%, 99%, and 100% of the time in Conditions 1 through 4, respectively (Fig. 3). (Chance behavior would be 50%.) Between 82% and 97% of subjects preferentially viewed the higher-probability-gain feature in each condition (Table 2; all ps < .001). In Conditions 1 and 2, all models except probability gain preferred G, making subjects’ preference for F especially striking. In Condition 3, 27 of 28 subjects preferred F, which optimized information gain, probability gain, and probability of certainty, rather than impact. In Condition 4, 28 of 29 subjects preferred to optimize the OED models, including probability gain, rather than the probability-of-certainty heuristic.

Fig. 3.

Preference for the higher-probability-gain feature (F) following experience-based learning in the four conditions of Experiment 1. The boxes give the interquartile range, with notches denoting the median subject in each condition. The outermost bars depict the range of the subjects, with the exception of 2 outlier subjects (those with values more than 10 times beyond the interquartile range, denoted by plus signs). Chance = 50% in each condition. See Table 2 for comparison with verbal statistics-based learning results.

Table 2.

Information-Acquisition Results for Experiments 1 and 2

	Percentage of subjects preferring higher-probability-gain feature (F)			Percentage of views to F in experience-based task
Condition	Experience-based task	Statistics-based task	Experience = statistics?	Median subject	Mean over all subjects
1	82***	27**	no****	97	77
2	82***	30*	no****	97	75
3	96****	65	no**	99	89
4	97****	58	no***	100	94

Note: In all conditions, the prior probabilities for categories a and b were P(a) = .70 and P(b) = .30. Table 1 gives the feature likelihoods in each condition. Two-tailed binomial tests were used to determine whether the number of subjects favoring F was different from chance in each condition. Two-tailed difference-of-proportions tests were used to determine whether equivalent proportions of subjects preferred F in the experience-based and summary-statistics-based tasks. In each condition, 28 to 29 subjects completed the experience-based task (in Experiment 1), and 43 to 45 subjects completed the statistics-based task (in Experiments 1 and 2).

^*p < .05.

^**p < .01.

^***p < .001.

^****p < .0001.

Summary-statistics-based task

After completing the experience-based learning and information-acquisition phases of the probabilistic plankton-categorization task, subjects were given an equivalent task in which environmental probabilities (prior probabilities and feature likelihoods) were presented verbally via summary statistics. (Gigerenzer & Hoffrage, 1995, called this the standard probability format.) This task used the Planet Vuma scenario (Skov & Sherman, 1986), in which the goal is to classify the species of invisible aliens (glom or fizo) by asking about features that the different species have in varying proportion (such as wearing a hula hoop or gurgling a lot). The prior probability of each species (e.g., P(glom) = 70%) and the likelihoods of each feature (e.g., for the feature hula, P(hula | glom) = 0% and P(hula | fizo) = 29%) exactly matched the values in the plankton task the subject had just completed (though this was not disclosed). An uninformative third feature (present in 100% of both species or in 0% of both species) was also included to ensure that subjects read and understood the information presented. Subjects were asked to rate, from most to least useful (in a rank ordering from 1 to 3), which of the features would be most helpful to enable them to categorize an alien as a glom or fizo.

Statistics-based results were much less clear than the experience-based results, and indistinguishable from chance in some conditions. It is interesting to note that the trend in every condition was for the feature with higher information gain (rather than probability gain) to be preferred. Were subjects consistent between the experience-based and statistics-based tasks? We performed a chi-square test in each condition to assess whether individual preferences following experience-based learning predicted preferences following summary-statistics-based learning. All four comparisons were nonsignificant, providing no evidence for within-subjects consistency, or inconsistency, or any relationship whatsoever between the modalities. This suggests that results from summary-statistics-based information-acquisition experiments in the literature may fail to predict behavior in naturalistic information-acquisition tasks (e.g., eye movements in natural scenes) in which people have personal experience with environmental probabilities.

Experiment 2: Summary-Statistics Versus Experience-Based Information Acquisition

Confidence intervals for subjects’ preferences between features were much broader in the summary-statistics-based task (in which subjects gave a rank order only) than in the comparatively data-rich experience-based task (in which there were 101 information-acquisition trials). We therefore obtained summary-statistics-based-task data from 85 additional University of California, San Diego, students. Subjects were randomly assigned to one of the same four conditions as in Experiment 1 and to either an alien- or plankton-categorization scenario. Each subject was randomly assigned to one of 96 possible randomizations of the given condition’s probabilities. Results in both scenarios were consistent with the results from the summary-statistics-based task in Experiment 1. We therefore aggregated all summary-statistics-based results in the analyses that follow.

Table 2 compares the experience- and statistics-based information-acquisition results in Experiments 1 and 2. In every condition, the percentage of subjects preferring F was different for the two types of learning. Experience-based learning led to preferring the feature with higher probability gain in every condition. Statistics-based learning led to a modal preference to maximize information gain in each condition. However, the statistics-based results were closer to chance than were the experience-based results in all conditions, and indistinguishable from chance in Conditions 3 and 4.

Experiment 3: How Robust Is the Preference for Probability Gain?

In Experiment 3, we explored possible limits in the circumstances in which subjects maximize probability gain. Experiment 3 was virtually identical to Experiment 1 in its design and subject pool.⁴

Condition 1

Would information gain or the possibility of a certain result “break the tie” in people’s choice of what feature to view when probability gain is indifferent? To address this, we tested a scenario in which both F and G have probability gain .25, yet F has higher information gain and is the only feature to offer the possibility of a certain result: P(a) = .50, P(f₁|a) = 0, P(f₁|b) = .50, P(g₁|a) = .25, and P(g₁|b) = .75. It is surprising that only about half of the subjects (12/22 = 55%) preferred F, even though its greater information and the possibility of certainty had zero cost in terms of probability gain.

Condition 2

In Condition 2, we modified Conditions 1 and 2 from Experiment 1 so that probability gain had a relatively marginal preference for F, whereas the other models had increased preference for G. We tested one such scenario: P(a) = .70, P(f₁|a) = 0, P(f₁|b) = .15, P(g₁|a) = .57, and P(g₁|b) = 0. In this condition, probability gain marginally prefers F (PStr = 9), whereas the other models more strongly prefer G (PStr for information gain, impact, and probability of certainty, respectively, are: −20, −35, and −35). Probability gain was maximized by 8 of 9 learners.

Condition 3

Finally, we modified Conditions 1 and 2 from Experiment 1 so that the F feature, taken alone, can never give a certain result: P(a) = .70, P(f₁|a) = .04, P(f₁|b) = .37, P(g₁|a) = .57, and P(g₁|b) = 0. F has higher probability gain than G. Yet G is the only feature to offer the possibility of a certain result and has higher information gain and impact than F. In this condition, 6 of 20 subjects (30%) preferred G. This environment is the only one we identified in which a nontrivial minority of subjects optimized something besides probability gain.

Taken together, our data strongly point to probability gain (or a substantially similar model) as the primary basis for the subjective value of information in categorization tasks.

General Discussion

This article reports the first information-acquisition experiment in which both

• environmental probabilities were designed to maximally differentiate theoretical predictions of competing models, and

• experience-based learning was used to convey environmental probabilities.

Previous studies did not distinguish among several models of information-acquisition behavior. Yet we obtained very clear results pointing to probability gain as the primary basis for the subjective value of information for categorization. Our within-subjects comparison of traditional summary-statistics-based presentation of environmental probabilities with experience-based learning is another contribution: The convincing lack of relationship between behavior in the two types of tasks is remarkable and should be explored further. For instance, the visual system may more effectively code statistics and contingencies than linguistic parts of the brain. As a practical matter, experience-based learning might be speeded by simultaneous presentation of multiple examples (Matsuka & Corter, 2008). Verbal-based information search might be facilitated by natural-frequency formats or explicit instruction in Bayesian reasoning (Gigerenzer & Hoffrage, 1995; Krauss, Martignon, & Hoffrage, 1999; Sedlmeier & Gigerenzer, 2001).

Treating evidence acquisition as an experimental-design problem broadens the “statistical man” approach, which originally focused on inferences people make given preselected data (Peterson & Beach, 1967). Key current questions include the following: (a) Does information acquisition in medical diagnosis, scientific-hypothesis testing, and word learning optimize probability gain? (b) Does the visual system optimize probability gain when directing the eyes’ gaze? and (c) Can people optimize criteria besides probability gain when necessary? Theories of the statistical human should aim to address these issues in a unified account of cognitive and perceptual learning and information acquisition.