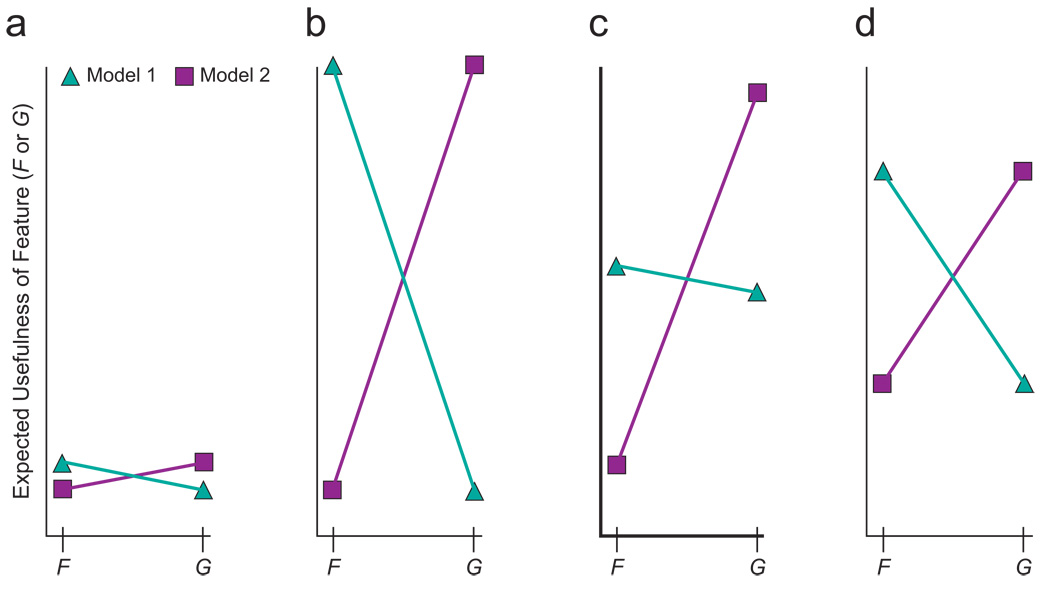
Fig. 2.

Four scenarios illustrating finding maximally informative features (F and G) to differentiate the predictions of competing theoretical models of the value of information (Model 1 and Model 2). The goal of optimization is to maximize disagreement strength (DStr)—which is based on the geometric mean of the two models’ absolute preference strengths—between the models. Because the optimization process generates feature likelihoods at random, the first step typically finds only weak disagreement between competing theoretical models of the value of information. In (a), Model 1 considers F to be slightly more useful than G, and Model 2 considers G to be slightly more useful than F. The shallow slopes of the connecting lines illustrate that the models’ (contradictory) preferences are weak, and DStr is low. An ideal scenario for experimental test is shown in (b). Model 1 holds that F is much more useful than G, whereas Model 2 has opposite and equally strong preferences. Thus, DStr is maximal. In (c), Model 2 strongly prefers G to F, and Model 1 marginally prefers F to G. This is not an ideal case to test experimentally. Because Model 1 is close to indifferent, DStr is low even though Model 2 has a strong preference. DStr is higher in (d) than in (c) because the models both have moderate (and contradictory) preferences.