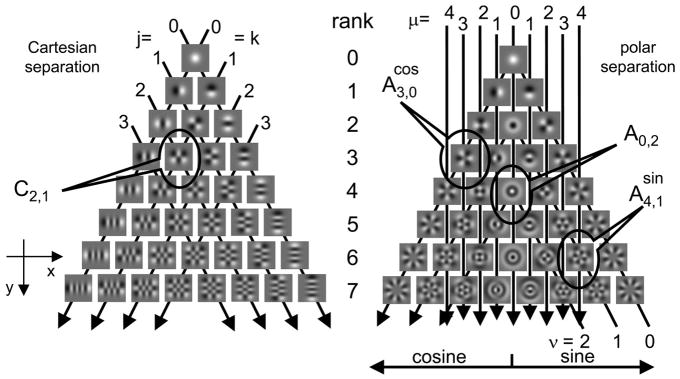
FIG. 1.

Two-dimensional Hermite (TDH) functions used in these experiments. Each family (Cartesian, left; polar, right) forms an orthonormal basis for 2-dimensional patterns and increases gradually in spatial extent and bandwidth as rank (row) increases. For the Cartesian functions, the indices j and k specify the number of zero-crossings along the x- and y-coordinates. Each index is constant along a set of parallel lines, as indicated by the arrows. Rank of a Cartesian function is equal to j + k. For the polar functions, the index ν specifies the number of zero-crossings along each radius and is constant along the inverted “vees” that begin at the bottom right, peak along the middle of the array, and then continue to the bottom left. Index μ specifies the number of zero-crossings along concentric circles and is constant along vertical lines as indicated by the down-pointing arrows. Rank of a polar function is equal to μ + 2v; the “cosine” and “sine” halves of the array contain the functions whose dependency on polar angle θ is given by cos (μθ) and sin (μθ), respectively, where θ is measured clockwise from the horizontal (x-) axis. Midline of the polar array contains the functions that are independent of θ.