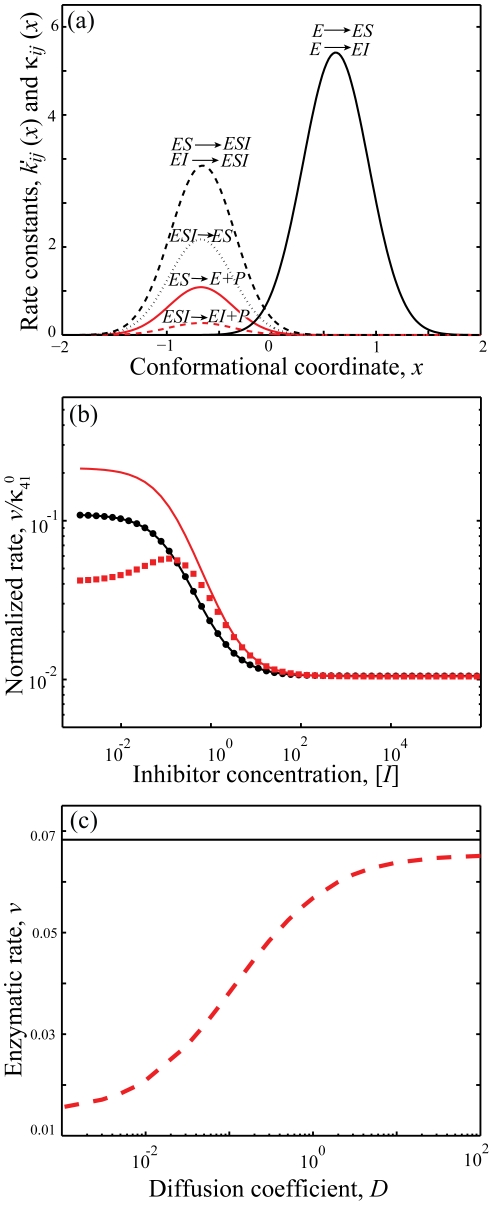
Figure 3. Numerical results for the partial noncompetitive inhibition reaction.

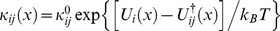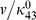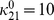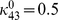a) Rate constants κ_ij (x) and k_ij (x) as function of the conformational coordinate x, with parameters given in Tables 3 and 4 calculated using Eq. (34) and . b) Normalized rate as a function of concentration [I] at a fixed concentration of [S] = 1. When catalytic reaction is fast with and Slow diffusion in ES conformation leads to an increase in the rate at low and intermediate inhibitor concentration followed by a decay (red squares), a deviation from the macroscopic rate law(red solid line) computed from equation (A.3). For slow catalysis (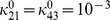, quasi-equilibrium limit) normalized rate 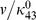has the same dependence on I concentration (black circles) as the macroscopic rate law(black solid line) calculated from equation (B.7). We use D_ES = 10⁻² and D_E = D_EI =  = D_ESI = 10² and the rest of parameters as in (a). c) Enzymatic rate as a function of conformational diffusion. We took all the diffusions to be the same D_E = D_ES = D_EI = D_ESI = D. For fast catalysis 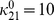and 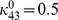the enzymatic rate decreases with decreased diffusion (red dashed line). In the quasi-equilibrium limit, when the catalysis is slow 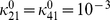the enzymatic rate does not depend on the diffusion coefficient (black solid line). Notably the same trend continues with further decrease in diffusion coefficients, D. We use [S] = 1, [I] = 0.1 and the remaining parameters as in (a, b).