Atomic Forces for Geometry-Dependent Point Multipole and Gaussian Multipole Models

Abstract

In standard treatments of atomic multipole models, interaction energies, total molecular forces, and total molecular torques are given for multipolar interactions between rigid molecules. However, if the molecules are assumed to be flexible, two additional multipolar atomic forces arise due to 1) the transfer of torque between neighboring atoms, and 2) the dependence of multipole moment on internal geometry (bond lengths, bond angles, etc.) for geometry-dependent multipole models. In the current study, atomic force expressions for geometry-dependent multipoles are presented for use in simulations of flexible molecules. The atomic forces are derived by first proposing a new general expression for Wigner function derivatives ∂D^l_m′m/∂Ω. The force equations can be applied to electrostatic models based on atomic point multipoles or Gaussian multipole charge density. Hydrogen bonded dimers are used to test the inter-molecular electrostatic energies and atomic forces calculated by geometry-dependent multipoles fit to the ab initio electrostatic potential (ESP). The electrostatic energies and forces are compared to their reference ab initio values. It is shown that both static and geometry-dependent multipole models are able to reproduce total molecular forces and torques with respect to ab initio, while geometry-dependent multipoles are needed to reproduce ab initio atomic forces. The expressions for atomic force can be used in simulations of flexible molecules with atomic multipoles. In addition, the results presented in this work should lead to further development of next generation force fields composed of geometry-dependent multipole models.

Introduction

Over the past few decades, molecular dynamic simulations have been routinely used to investigate the structure and dynamics of liquids^1–3 and large molecular systems such biochemical structures^4,5. For systems of this size, ab initio methods are too costly and empirical force fields are used to model intermolecular interactions. In recent years, much effort has been devoted to improving the accuracy and sophistication of force fields. For example, polarization models^6–10 have been proposed in order to improve point charge force fields^11–13. Models^14–17 for the exchange-repulsion energy are being investigated. Atomic multipoles^18–22 have been used in force fields^23–28 in order to account for the anisotropy missing in atomic point charge models. Models^29–34 for molecular charge density, such as Gaussian multipoles^34–38, have been studied in order to accurately account for the penetration error^18,39 associated with atomic point multipoles at short range separations. Alternatively, damping functions^39–41 have been proposed in order to correct for short range inter-molecular interactions. In addition, geometry-dependent electrostatic models, in which the charge parameters are a function of geometry, are being explored^42–46. In order to implement the force field models into molecular dynamics simulations, analytic derivatives of energy are needed to calculate atomic forces.

In standard treatments of multipolar torque and force, the interacting molecules are assumed to be rigid^47–49. For rigid molecules, the problem of calculating forces is simplified since only the total molecular force and total molecular torque are required^50,51. Stone^47,48 and co-workers have derived first and second derivatives for total molecular force/torque expressions between rigid point multipoles by expressing the multipolar energies as a sum of Cartesian components. Hättig⁴⁹ has found efficient expressions for first and second derivatives for total molecular force/torque by directly differentiating the spherical tensor multipole interactions. The expressions given in these works are valid for rigid molecules or rigid molecular fragments. However, for flexible molecules, additional terms contribute to the atomic multipolar force, which arise due to the dependence of multipole moment $Q_{lm}^a$ on atomic position r_a′. A major aim of this report is to provide compact expressions for evaluating atomic multipolar forces by proposing a method to evaluate $\partial Q_{lm}^a/\partial {\mathbf{r}}_{a\prime }$.

In order to better illustrate the above description of atomic multipolar force, suppose $Q_{lm}^a$ is a set of atomic multipole moments evaluated in the global frame on atom a at position r_a in a molecule A. Similarly, let $Q_{l\prime m\prime }^b$ be a set of atomic multipoles on atom b at position r_b in a molecule B. The multipole interaction energy U between molecules A and B is given by¹⁸

$$U={\displaystyle \sum _{a\in A}{\displaystyle \sum _{b\in B}{\displaystyle \sum _{lm}{\displaystyle \sum _{l\prime m\prime }{Q}_{lm}^a{T}_{lm;l\prime m\prime }^{ab}({\mathbf{r}}_{ab})Q_{l\prime m\prime }^b,}}}}$$ (1)

where r_ab ≡ r_a– r_b and $T_{lm;l\prime m\prime }^{ab}$ is a multipole interaction matrix. For atomic point multipoles, $T_{lm;l\prime m\prime }^{ab}$ is expressed in terms of spherical harmonics Y_LM by^18,52

$$T_{lm;l\prime m\prime }^{ab}(\mathbf{r})=\frac{{(-1)}^{l\prime }}{(2L-1)!!}\sqrt{\frac{4\pi }{2L+1}}\sqrt{\left(\begin{array}{c}L+M\\ l+m\end{array}\right)\left(\begin{array}{c}L-M\\ l-m\end{array}\right)}\frac{Y_{LM}^{*}(\widehat{\mathbf{r}})}{r^{L+1}}$$ (2)

where L ≡ l + l′ and M ≡ m + m′. Recently, Giese and York^37,38 have derived a similar expression for $T_{lm;l\prime m\prime }^{ab}$ and its Cartesian gradient for contracted solid harmonic Gaussian multipole functions.

The multipolar interaction energy U in eqn. 1 can be re-expressed as

$$\begin{array}{cc}U={\displaystyle \sum _{a\in A}{\displaystyle \sum _{lm}{Q}_{lm}^a{\phi }_{lm}^{*}({\mathbf{r}}_a),}}\hfill & {\phi }_{lm}^{*}({\mathbf{r}}_a)\equiv {\displaystyle \sum _{b\in B}{\displaystyle \sum _{l\prime m\prime }{T}_{lm;l\prime m\prime }^{ab}{Q}_{l\prime m\prime }^b,}}\hfill \end{array}$$ (3)

where ${\phi }_{lm}^{*}({\mathbf{r}}_a)$ is the ‘multipolar potential’ on atom a arising from molecule B. The atomic force on atom a′ in molecule A is given by the negative gradient of energy U with respect to r_a′ as

$${\mathbf{F}}_{a\prime }=-{\displaystyle \sum _{a\in A}{\displaystyle \sum _{lm}\frac{\partial Q_{lm}^a}{\partial {\mathbf{r}}_{a\prime }}{\phi }_{lm}^{*}({\mathbf{r}}_a)}}-{\displaystyle \sum _{lm}{Q}_{lm}^{a\prime }\frac{\partial {\phi }_{lm}^{*}({\mathbf{r}}_{a\prime })}{\partial {\mathbf{r}}_{a\prime }}}.$$ (4)

The gradient of ${\phi }_{lm}^{*}({\mathbf{r}}_{a\prime })$ with respect to r_a′ can be expressed using the known expressions^34,37 for the Cartesian gradient of the interaction matrix $T_{lm;l\prime m\prime }^{ab}$. In order to calculate the atomic force F_a′ for flexible molecules, a method of evaluating $\partial Q_{lm}^a/\partial {\mathbf{r}}_{a\prime }$ in eqn. 4 is needed. However, for rigid molecules, only the total molecular force F_tot given by

$${\mathbf{F}}_{tot}={\displaystyle \sum _{a\prime \in A}{\mathbf{F}}_{a\prime }}=-{\displaystyle \sum _{a\prime \in A}{\displaystyle \sum _{lm}{Q}_{lm}^{a\prime }\frac{\partial {\phi }_{lm}^{*}({\mathbf{r}}_{a\prime })}{\partial {\mathbf{r}}_{a\prime }}}}.$$ (5)

is needed. The term containing $\partial Q_{lm}^a/\partial {\mathbf{r}}_{a\prime }$ does not contribute to F_tot, since $Q_{lm}^a$ depends on relative atomic positions and is translationally invariant, i.e. ${\displaystyle {\sum }_{a\prime }\partial Q_{lm}^a/\partial {\mathbf{r}}_{a\prime }=0}$.

The functional dependence of $Q_{lm}^a({\mathbf{r}}_1,{\mathbf{r}}_2..)$ on atomic position r_a′ is described below. Since the atomic multipole moment in the global frame $Q_{lm}^a$ can assume an arbitrary orientation, the standard convention¹⁸ is to define multipole moments in a local frame of the atom $Q_{lm\prime }^{a,Loc}$ and rotate to the global frame

$$Q_{lm}^a={\displaystyle \sum _{m\prime =-l}^l{D}_{m\prime m}^l[{\mathbf{R}}_a^{-1}]Q_{lm\prime }^{a,Loc}},$$ (6)

where D^l_m′m is a Wigner rotation matrix^53–57 and R_a is a Cartesian rotation matrix defining the local to global frame transformation for atom a. The multipoles in the local frame of the atom $Q_{lm\prime }^{a,Loc}(\eta )$ are assumed to be an explicit function of internal geometry variables η (bond lengths, bond angles, etc.) for ‘geometry-dependent’ multipoles. Thus, $Q_{lm\prime }^{a,Loc}$ depends on atomic positions r_a′ through the internal degrees of freedom. If the local frame multipoles are constant and do not depend depend on η, i.e. $\partial Q_{lm\prime }^{a,Loc}/\partial \eta =0$, then the multipoles are called ‘static’.

The Wigner rotation matrix $D_{m\prime m}^l[{\mathbf{R}}_a^{-1}]$ is a function of the local to global Cartesian rotation matrix R_a, which in turn is a function of atomic positions r_a′. For a given atom, the local frame is commonly defined with respect to the relative positions of the atom and its neighbors^23,58,59. For example, the local frame of a nitrogen atom in an ammonia molecule is given in Figure 1. The local frame for the nitrogen atom with label a is defined with respect to the relative positions of the H1 hydrogen with label ‘N1’ and the H2 hydrogen with label ‘N2’. This type of local reference frame definition is general and can be applied to any atom in a non-linear molecule.

Figure 1.

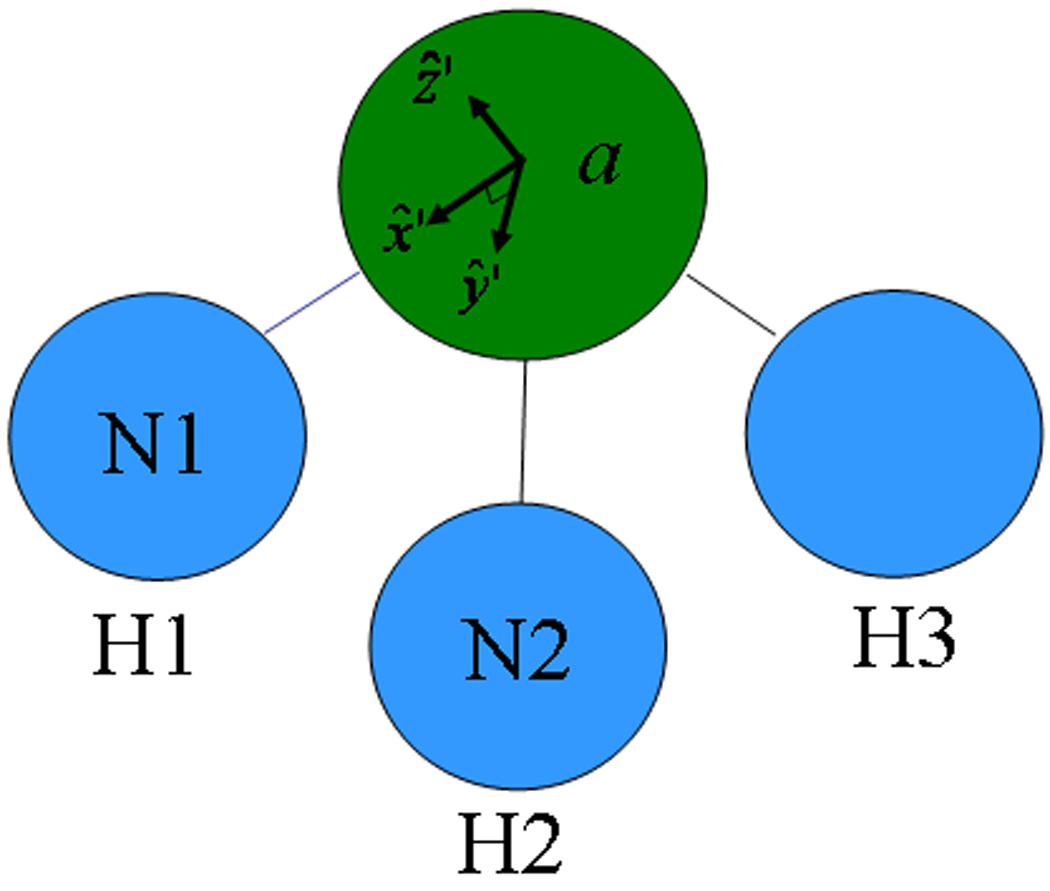
The local coordinate system on a nitrogen atom with label ‘a’ in an ammonia molecule is defined with respect to its neighboring hydrogen H1 with label ‘N1’ and another hydrogen H2 with label ‘N2’. The local x̂′ axis is defined along the N1-a bond length, the ŷ′ axis is defined in the N1-a-N2 plane, and the ẑ′ axis is the cross product of x̂′ and ŷ′. This type of local frame can be defined for any atom in a non-linear molecule.

Interestingly, the local frame definition in terms of neighboring atoms is arbitrary, since the local frame of the nitrogen in ammonia from Figure 1 could have also been defined with respect to the relative positions of the H1 and H3 hydrogens or the H2 and H3 hydrogens. Different local frame definitions lead to different functional dependencies of the local to global Cartesian rotation matrix R_a on neighboring atomic positions r_a′, which lead to different atomic forces if the multipoles are static, i.e.$\partial Q_{lm\prime }^{a,Loc}/\partial \eta =0$. However, if the multipoles are geometry-dependent, the atomic forces are shown to be independent of how the local frames are defined (see the SI for an example).

The gradient of atomic multipole with respect to atomic position can be found by differentiating eqn. 6

$$\frac{\partial Q_{lm}^a}{\partial {\mathbf{r}}_{a\prime }}={\displaystyle \sum _{m\prime =-l}^l\frac{\partial D_{m\prime m}^l[{\mathbf{R}}_a^{-1}]}{\partial {\mathbf{r}}_{a\prime }}{Q}_{lm\prime }^{a,Loc}+D_{m\prime m}^l[{\mathbf{R}}_a^{-1}]\frac{\partial Q_{lm\prime }^{a,Loc}}{\partial {\mathbf{r}}_{a\prime }}}.$$ (7)

Expressions for Wigner function derivatives ∂D^l_m′m/∂Ω are known⁵³ for the special cases when Ω is an Euler angle or represents an infinitesimal rotation. In principle, one could employ Euler angles as an intermediate variable and calculate ∂D^l_m′m/∂r_a′ by a chain-rule argument. However, this procedure is complicated, and it can be shown that the necessary transformations involving Euler angles contain singularities at certain discrete orientations. In this study, a general expression for ∂D^l_m′m/∂Ω is presented given its corresponding Cartesian rotation matrix derivative (∂R/∂Ω)R⁻¹, where Ω is an arbitrary variable. By letting Ω be a component of atomic position, an expression for (∂R/∂r_a′)R⁻¹ is derived and used to evaluate ∂D^l_m′m/∂r_a′ directly. Our result for ∂D^l_m′m/∂r_a′ does not suffer from the singularity problems associated with a procedure based on Euler angles.

The term containing $\partial Q_{lm\prime }^{a,Loc}/\partial {\mathbf{r}}_{a\prime }$ in eqn. 7 can be evaluated from atomic gradients of internal geometry variables^60–64 ∂η/∂r_a′

$$\frac{\partial Q_{lm\prime }^{a,Loc}}{\partial {\mathbf{r}}_{a\prime }}={\displaystyle \sum _{\eta }\frac{\partial Q_{lm\prime }^{a,Loc}}{\partial \eta }\frac{\partial \eta }{\partial {\mathbf{r}}_{a\prime }}},$$ (8)

where η is a bond length, bond angle, improper dihedral angle, or dihedral angle. In the present study, the expressions for multipolar atomic force are tested on geometry-dependent atomic multipoles fit to the electrostatic potential (ESP). The geometry dependence of the atomic multipoles in the local frame $Q_{lm\prime }^{a,Loc}(\eta )$ is represented by a truncated linear Taylor series in internal geometry η

$$Q_{lm\prime }^{a,Loc}(\eta )=Q_{lm\prime }^{a,Loc}({\eta }_0)+{\displaystyle \sum _{\eta }(\eta -{\eta }_0)\frac{\partial Q_{lm\prime }^{a,Loc}}{\partial {\eta }_0}}$$ (9)

where η₀ represents an internal geometry variable of the molecule for any reference geometry which is taken to be the optimized equilibrium geometry, $Q_{lm\prime }^{a,Loc}({\eta }_0)$ is an ESP-fitted atomic multipole in the local frame of atom a at the equilibrium geometry, and $\partial Q_{lm\prime }^{a,Loc}/\partial {\eta }_0$ is the finite difference derivative of $Q_{lm\prime }^{a,Loc}$ with respect to perturbing the variable η₀ at the equilibrium geometry. In addition, static multipoles are studied by setting $\partial Q_{lm\prime }^{a,Loc}/\partial {\eta }_0$ equal to zero.

The expressions for atomic multipolar force are applied to models based on atomic point multipole and Gaussian multipole^34–38 charge density. In a recent work³⁴, we have proposed an electrostatic model based on charge density which is composed of a single Slater-type^65,66 contracted Gaussian multipole^34,37 and positive nucleus on each atom. The Gaussian multipoles $Q_{lm}^{a,Loc}$ and a single Slater-type exponent parameter λ are fit to the ab initio ESP and tested by comparing electrostatic dimer energies, inter-molecular density overlap integrals, and molecular multipole moments with their ab initio values.³⁴ In contrast to atomic point multipole models which suffer from the penetration error^18,39 at short range separation, Gaussian multipoles are able to accurately account for electrostatic interactions at short separation distances. However, atomic point multipoles can be studied by taking the large exponent limit of Gaussian multipoles³⁵. In addition, the local frame atomic Gaussian multipole moments $Q_{lm\prime }^{a,Loc}(\eta )$ were shown to be smooth functions of bond length and bond angle for the case of water.³⁴

In the present study, inter-molecular electrostatic energies and atomic forces are calculated on hydrogen bonded dimers using geometry-dependent multipole models and compared to their ab initio reference values. The inter-molecular ab initio electrostatic energies are calculated at the Hatree-Fock level by the Restrained Variation Space^67,68 (RVS) decomposition method, while inter-molecular ab initio electrostatic atomic forces are calculated as finite difference derivatives of RVS electrostatic energies. In contrast to static multipole models, it is shown that geometry-dependent atomic multipoles are capable of reproducing ab initio electrostatic forces. However, both static and geometry-dependent multipole models are able to reproduce total molecular forces and total molecular torques with respect to ab initio.

This work will be organized as follows. In the following Methods section, the atomic multipole force expressions are evaluated. A general expression for ∂D^l_m′m/∂Ω is derived from elementary properties of spherical harmonics^69,70 Y_lm and Wigner^53–57 functions D^l_m′m, which are summarized in the appendix. The general result for ∂D^l_m′m/∂Ω is used to derive an equation for the torque and atomic force on a multipole. Computational details describing the ab initio calculations and how the multipoles are fit to the ESP are given. In the Results section, intermolecular electrostatic energies atomic forces, molecular forces, and molecular torques calculated on hydrogen bonded dimers are given for static/geometry-dependent multipole models and compared to their respective ab initio values. In addition, the molecular moments calculated by static/geometry-dependent atomic multipoles are plotted as a function of bond length and bond angle for the illustrative case of water. Lastly, the results are summarized in the Conclusion section. There is supplementary information (SI), which contains additional results and mathematical details not included in the main text.

Methods

Atomic Multipolar Forces

The atomic mutipolar forces are found by inserting the gradient of multipole moment in eqn. 7 into eqn. 4. For convenience, the atomic force is separated into three terms, which we call the ‘translational’, ‘orientational’, and ‘geometry-dependent’ parts:

$${\mathbf{F}}_{a\prime }^{trans}=-{\displaystyle \sum _{lm}{Q}_{lm}^{a\prime }\frac{\partial {\phi }_{lm}^{*}({\mathbf{r}}_{a\prime })}{\partial {\mathbf{r}}_{a\prime }}},$$ (10)

$${\mathbf{F}}_{a\prime }^{\mathit{\text{orient}}}=-{\displaystyle \sum _{a\in A}{\displaystyle \sum _{l,m,m\prime }\frac{\partial D_{m\prime m}^l[{\mathbf{R}}_a^{-1}]}{\partial {\mathbf{r}}_{a\prime }}{Q}_{lm\prime }^{a,Loc}{\phi }_{lm}^{*}({\mathbf{r}}_a)}},$$ (11)

$${\mathbf{F}}_{a\prime }^{\mathit{\text{geom}}.\mathit{\text{depend}}.}=-{\displaystyle \sum _{a\in A}{\displaystyle \sum _{l,m,m\prime }{D}_{m\prime m}^l[{\mathbf{R}}_a^{-1}]\frac{\partial Q_{lm\prime }^{a,Loc}}{\partial {\mathbf{r}}_{a\prime }}{\phi }_{lm}^{*}({\mathbf{r}}_a)}}.$$ (13)

The translational force is found from the gradient of ${\phi }_{lm}^{*}$ which can be calculated by the known expressions^34,37 for the gradient of the interaction matrix $T_{lm;l\prime m\prime }^{ab}$. For the orientational force, the sum over atom a only includes atoms in which a′ is used to define the local to global transformation for atom a. An expression for the orientational force is given in a later section after ∂D^l_m′m/∂r_a′ is evaluated.

The geometry-dependent force can be found by inserting eqn. 8 into eqn. 13

$${\mathbf{F}}_{a\prime }^{\mathit{\text{geom}}.\mathit{\text{depend}}.}=-{\displaystyle \sum _{\eta }{E}_{\eta }\frac{\partial \eta }{\partial {\mathbf{r}}_{a\prime }}},$$ (14)

where E_η is defined by

$$\begin{array}{cc}{E}_{\eta }\equiv {\displaystyle \sum _{a\in A}{\displaystyle \sum _{lm}{Q}_{lm}^{a,\eta }{\phi }_{lm}^{*}({\mathbf{r}}_a)}},\hfill & Q_{lm\prime }^{a,\eta }\equiv {\displaystyle \sum _{m\prime }{D}_{m\prime m}^l[{\mathbf{R}}_a^{-1}]\frac{\partial Q_{lm\prime }^{a,Loc}}{\partial \eta }}\hfill \end{array}.$$ (15)

The expressions for geometry-dependent force in eqn. 14 and 15 are valid for arbitrary, but explicit functions of local frame multipole moment $Q_{lm\prime }^{a,Loc}(\eta )$ about internal geometry η. In the present study, $Q_{lm\prime }^{a,Loc}(\eta )$ is a truncated linear Taylor series in internal geometry given by eqn. 9, where the constant values $Q_{lm\prime }^{a,Loc}({\eta }_0)$ and $\partial Q_{lm\prime }^{a,Loc}/\partial {\eta }_0$ are fit to the ab initio electrostatic potential. Note the internal geometry variables η are translationally invariant, ∑_a′ ∂η/∂r_a′ = 0, which implies the total molecular geometry-dependent force is zero,

$${\displaystyle \sum _{a\prime }{\mathbf{F}}_{a\prime }^{\mathit{\text{geom}}.\mathit{\text{depend}}.}}=0.$$ (16)

Wigner Rotation Matrix Derivatives

In this section, a general expression for ∂D^l_m′m/∂Ω is derived. In the appendix, mathematical background information needed in the following derivation is given. Properties of spherical harmonics Y_lm (θ,φ) ^69,70, Wigner rotation matrices^53–57 D^l_m′m[R], and Cartesian rotation matrix derivatives (∂R/∂Ω) R⁻¹ are summarized.

The expression for the Wigner rotation matrix in eqn. A.12 can be expressed symbolically as an integral over a unit sphere in terms of spherical harmonics Y_lm and the ξ variables defined in eqns. A.4 by

$$D_{m\prime m}^l[\mathbf{R}]={\displaystyle \int d\widehat{\xi }{Y_{lm\prime }}^{*}(\widehat{\xi })Y_{lm}(\widehat{\xi }\prime )}\equiv \langle Y_{lm\prime }(\xi )|Y_{lm}(\xi \prime )\rangle .$$ (17)

Since ξ_i is proportional to Y_1i by eqn. A.5, the transformed ξ_i′ variables are given by eqn. A.11 with l = 1 as

$${\xi }_i\prime ={\displaystyle \sum _{j=-1}^1{D}_{ji}^1[\mathbf{R}]{\xi }_j}.$$ (18)

If the Cartesian rotation matrix R is a function of an orientation variable Ω, then the transformed coordinates ξ_i′ are also functions of Ω, i.e. ξ_i′ = ξ_i′(Ω), and the derivative of ξ_i′ with respect to Ω is given by differentiating eqn. 18 as

$$\frac{\partial }{\partial \mathrm{\Omega }}{\xi }_i\prime ={\displaystyle \sum _{j=-1}^1\frac{\partial D_{ji}^1[\mathbf{R}]}{\partial \mathrm{\Omega }}{\xi }_j}={\displaystyle \sum _{j=-1}^1{D}_{ji}^1[\frac{\partial \mathbf{R}}{\partial \mathrm{\Omega }}]{\xi }_j}.$$ (19)

The last step follows from the fact that D¹_ji[R] is a linear function of the matrix elements of R(Ω) by eqns. A.14 – A.16.

The functional dependence of D^l_m′m on Ω is given by

$$D_{m\prime m}^l[\mathbf{R}(\mathrm{\Omega })]=\langle Y_{lm\prime }(\xi )|Y_{lm}(\xi \prime (\mathrm{\Omega }))\rangle .$$ (20)

The derivative ∂D^l_m′m/∂Ω can be found by differentiating both sides of eqn. 20 and applying eqns. 19 and A.9

$$\begin{array}{cc}\frac{\partial }{\partial \mathrm{\Omega }}{D}_{m\prime m}^l[\mathbf{R}(\mathrm{\Omega })]\hfill & ={\displaystyle \sum _{i=-1}^1\langle Y_{lm\prime }(\xi )|\frac{\partial Y_{lm}}{\partial {\xi }_i\prime }\frac{\partial {\xi }_i\prime }{\partial \mathrm{\Omega }}\rangle }\hfill \\ \hfill & ={\displaystyle \sum _{i=-1}^1{\displaystyle \sum _{j=-1}^1{C}_{lm}^i{D}_{ij}^1[\frac{\partial \mathbf{R}}{\partial \mathrm{\Omega }}]\langle Y_{lm\prime }(\xi )|{\xi }_j{Y}_{l-1,m-i}(\xi \prime )\rangle }}\hfill \end{array}$$ (21)

The inverse relation ${\xi }_j={\displaystyle {\sum }_{k=-1}^1{D}_{kj}^1[{\mathbf{R}}^{-1}]{\xi }_k\prime }$ is substituted into the right side of eqn. 21 and eqn. A.6 is applied to obtain the desired result for ∂D^l_m′m/∂Ω in terms of D^l_m′m

$$\begin{array}{cc}\frac{\partial }{\partial \mathrm{\Omega }}{D}_{m\prime ,m}^l[\mathbf{R}(\mathrm{\Omega })]\hfill & ={\displaystyle \sum _{i,j,k=-1}^1{C}_{lm}^i{D}_{ji}^1[\frac{\partial \mathbf{R}}{\partial \mathrm{\Omega }}]D_{kj}^1[{\mathbf{R}}^{-1}]\langle Y_{lm\prime }(\xi )|{\xi }_k\prime Y_{l-1,m-i}(\xi \prime )\rangle }\hfill \\ \hfill & ={\displaystyle \sum _{i=-1}^1{\displaystyle \sum _{k=-1}^1{B}_{l-1,m-i}^k{C}_{lm}^i{D}_{ki}^1[{\mathbf{R}}^{-1}\frac{\partial \mathbf{R}}{\partial \mathrm{\Omega }}]D_{m\prime ,m-i+k}^l[\mathbf{R}]}}\hfill \end{array}.$$ (22)

This central result is a complete expression for ∂D^l_m′m/∂Ω in terms of the constants B^k_lm (eqn. A.8) and Cⁱ_lm (eqn. A.10) and the Cartesian rotation matrix derivative R⁻¹(∂R/∂Ω).

A second relation can be found by first expressing eqn. 22 as

$$\frac{\partial }{\partial \mathrm{\Omega }}{D}_{m\prime ,m}^l[\mathbf{R}(\mathrm{\Omega })]={\displaystyle \sum _{i,j,k=-1}^1{B}_{l-1,m-i}^k{C}_{lm}^i{D}_{kj}^1[{\mathbf{R}}^{-1}]D_{m\prime ,m-i+k}^l[\mathbf{R}]\frac{\partial }{\partial \mathrm{\Omega }}(D_{ji}^1[\mathbf{R}])}$$ (23)

After taking the complex conjugate of eqn. 23, interchanging m′ with m, interchanging R with R⁻¹, and applying eqn. A.13, a second expression for ∂D^l_m′m/∂Ω becomes,

$$\frac{\partial }{\partial \mathrm{\Omega }}{D}_{m\prime m}^l[\mathbf{R}(\mathrm{\Omega })]={\displaystyle \sum _{i=-1}^1{\displaystyle \sum _{k=-1}^1{B}_{l-1,m\prime -i}^k{C}_{lm\prime }^i{D}_{ik}^1[\frac{\partial \mathbf{R}}{\partial \mathrm{\Omega }}{\mathbf{R}}^{-1}]D_{m\prime -i+k,m}^l[\mathbf{R}]}}.$$ (24)

It is straightforward to show that second and higher order derivatives can be expressed in terms of lower order derivatives. In sections S6, S7, and S8 of the SI, eqns. 22 and 24 are evaluated for the special cases when Ω represents an infinitesimal rotation, an Euler angle, and a quaternion, respectively. For the special cases when Ω is an Euler angle or represents an infinitesimal rotation, the results for ∂D^l_m′m/∂Ω agree with those found in Varshalovich⁵³ et al. However, neither the results for Euler angles or quaternions are needed in the following discussions on torque and force.

Torque and Infinitesimal Rotations

In this section, an expression for the torque applied to a multipole in an external field is derived using the expression for ∂D^l_m′m/∂Ω (eqn. 24) given in the previous section. The results for torque are needed in the following section on orientational force. A similar result for torque has been given by Hättig⁴⁹ for the case of two interacting point multipoles, which are evaluated in a rotated coordinate frame. Below, an expression for torque is found when the multipoles are evaluated in the global frame.

The p^th component of torque τ_a,p acting upon a multipole $Q_{lm}^a$ on atom a with respect to r_a is defined by the negative partial derivative of energy U (eqn. 3) with respect to a rotation of the multipole $Q_{lm}^a$ about the p^th coordinate axis as⁴⁸ while keeping the molecule fixed

$${\mathbf{\tau }}_{a,p}=-{\left(\frac{\partial U}{\partial \mathrm{\Phi }}\right)}_{{\widehat{x}}_p}=-{\displaystyle \sum _{lm}{\left(\frac{\partial Q_{lm}^a}{\partial \mathrm{\Phi }}\right)}_{{\widehat{x}}_p}{\phi }_{lm}^{*}({\mathbf{r}}_a)}.$$ (25)

In the following section, this definition for torque is shown to reproduce the mechanical expression for torque τ ≡ r × F. After inserting eqn. 6 into eqn. 25 and applying eqn A.13, the torque on multipole a becomes

$${\mathbf{\tau }}_{a,p}=-{\displaystyle \sum _{l,m,m\prime }{\left(\frac{\partial D_{mm\prime }^l[{\mathbf{R}}_a]}{\partial \mathrm{\Phi }}\right)}_{{\widehat{x}}_p}^{*}{Q}_{lm\prime }^{a,Loc}{\phi }_{lm}^{*}({\mathbf{r}}_a)},$$ (26)

It is shown in Goldstein⁵⁰ that a partial derivative of a vector ν with respect to a rotation about the p^th coordinate axis x̂_p (p = 1, 2, 3 for x, y, z) is given by

$${\left(\frac{\partial \mathbf{\nu }}{\partial \mathbf{\Phi }}\right)}_{{\widehat{x}}_p}={\widehat{x}}_p\times \mathbf{\nu }={\mathbf{M}}_p\mathbf{\nu },$$ (27)

where x̂_p × ν represents a vector cross product between x̂_p and ν, and M_p is an antisymmetric infinitesimal rotation matrix about x̂_p defined by

$$\begin{array}{ccc}{\mathbf{M}}_1\equiv \left(\begin{array}{ccc}0& 0& 0\\ 0& 0& -1\\ 0& 1& 0\end{array}\right),\hfill & {\mathbf{M}}_2\equiv \left(\begin{array}{ccc}0& 0& 1\\ 0& 0& 0\\ -1& 0& 0\end{array}\right),\hfill & {\mathbf{M}}_3\equiv \left(\begin{array}{ccc}0& -1& 0\\ 1& 0& 0\\ 0& 0& 0\end{array}\right).\hfill \end{array}$$ (28)

By comparing eqns. 27 and A.18, it can be inferred that

$${\left(\frac{\partial \mathbf{R}}{\partial \mathbf{\Phi }}\right)}_{{\widehat{x}}_p}{\mathbf{R}}^{-1}={\mathbf{M}}_p.$$ (29)

After inserting eqns. 29 and 24 into eqn. 26, the torque becomes

$${\mathbf{\tau }}_{a,p}=-{\displaystyle \sum _{l,m}{\phi }_{lm}^{*}({\mathbf{r}}_a){\displaystyle \sum _{ik}{B}_{l-1,m-i}^k{C}_{lm}^i{D}_{ik}^1{[{\mathbf{M}}_p]}^{*}}{Q}_{l,m-i+k}^a}.$$ (30)

After evaluating D¹[M_p] from eqns. A.14 – A.16 and inserting the constants for B^k_lm (eqn. A.8) and Cⁱ_lm (eqn. A.10) into eqn. 30, the explicit expressions for torque becomes

$${\mathbf{\tau }}_{a,1}=-\frac{i}{2}{\displaystyle \sum _{lm}\left(K_{lm}^{-}{Q}_{lm-1}^a+K_{lm}^{+}{Q}_{lm+1}^a\right){\phi }_{lm}^{*}({\mathbf{r}}_a)},$$ (31)

$${\mathbf{\tau }}_{a,2}=\frac{1}{2}{\displaystyle \sum _{lm}\left(K_{lm}^{-}{Q}_{lm-1}^a-K_{lm}^{+}{Q}_{lm+1}^a\right){\phi }_{lm}^{*}({\mathbf{r}}_a)},$$ (32)

$${\mathbf{\tau }}_{a,3}=-i{\displaystyle \sum _{lm}m{Q}_{lm}^a{\phi }_{lm}^{*}({\mathbf{r}}_a)}.$$ (33)

where $K_{lm}^{\pm }\equiv \sqrt{(l\pm m+1)(l\mp m)}$. Eqns. 31 – 33 can also be derived by inserting the result for the Wigner function derivative with respect to infinitesimal rotations ${(\partial D_{m\prime m}^l/\partial \mathrm{\Phi })}_{{\widehat{x}}_p}$ given by Varshalovich⁵³ et al. or in section S6 of the SI into eqn. 26.

Orientational Force

The expression for orientation force in eqn. 11 can be rewritten as

$${\mathbf{F}}_{a\prime }^{\mathit{\text{orient}}}={\displaystyle \sum _{a\in A}{\mathbf{F}}_{a\to a\prime }^{\mathit{\text{orient}}}}$$ (34)

where ${\mathbf{F}}_{a\to a\prime }^{\mathit{\text{orient}}}$ is the orientation force contribution to atom a′ from R_a(r_a′) given by

$${\mathbf{F}}_{a\to a\prime }^{\mathit{\text{orient}}}=-{\displaystyle \sum _{l,m,m\prime }\frac{\partial D_{m\prime m}^l[{\mathbf{R}}_a^{-1}]}{\partial {\mathbf{r}}_{a\prime }}{Q}_{lm\prime }^{a,Loc}{\phi }_{lm}^{*}({\mathbf{r}}_a)}$$ (35)

Note that ${\mathbf{F}}_{a\to a\prime }^{\mathit{\text{orient}}}$ is non-zero only if a′ is used to define the local to global transformation for atom a, i.e. a′ = a, N1, N2. The result for ${\mathbf{F}}_{a\to a\prime }^{\mathit{\text{orient}}}$ is found by first calculating ∂D^l_m′m/∂r_a′,q (a′ = a, N1, N2; q = 1, 2, 3 for x, y, z) for the general type of local frame definition given in Figure 1. From eqn. 24, ∂D^l_m′m/∂r_a′,q can be evaluated by first calculating $(\partial {\mathbf{R}}_a/\partial {\mathbf{r}}_{a\prime ,q}){\mathbf{R}}_a^{-1}$. In the SI, $(\partial {\mathbf{R}}_a/\partial {\mathbf{r}}_{a\prime ,q}){\mathbf{R}}_a^{-1}$ is derived for the type of local coordinate system defined in Figure 1 and given by

$$\frac{\partial {\mathbf{R}}_a}{\partial {\mathbf{r}}_{a\prime ,q}}{\mathbf{R}}_a^{-1}={\displaystyle \sum _{t=1}^3{X}_t^{a\prime ,q}{\mathbf{M}}_t},(a\prime =a,\mathrm{N}1,\mathrm{N}2;q=1,2,3)$$ (36)

where M_t are the infinitesimal rotation matrices given in eqn. 28 and $X_t^{a\prime ,q}$ are geometric functions defined by

$$\begin{array}{c}{X}_t^{\mathrm{N}1,q}=-\left(\frac{1}{{\mathbf{\alpha }}^2}{({\widehat{\mathbf{x}}}_q\times \mathbf{\alpha })}_t+\frac{\mathbf{\alpha }\cdot \mathbf{\beta }}{{\mathbf{\alpha }}^2[{\mathbf{\alpha }}^2{\mathbf{\beta }}^2-{(\mathbf{\alpha }\cdot \mathbf{\beta })}^2]}{(\mathbf{\alpha }\times \mathbf{\beta })}_q{\mathbf{\alpha }}_t\right)\hfill \\ X_t^{\mathrm{N}2,q}=\frac{{\left(\mathbf{\alpha }\times \mathbf{\beta }\right)}_q{\mathbf{\alpha }}_t}{{\mathbf{\alpha }}^2{\mathbf{\beta }}^2-{(\mathbf{\alpha }\cdot \mathbf{\beta })}^2}\hfill \\ X_t^{a,q}=-(X_t^{\mathrm{N}1,q}+X_t^{\mathrm{N}2,q})\hfill \end{array},$$ (37)

where α ≡ r_N1 – r_a and β = r_N2 – r_a are bond vectors. Note that the $X_t^{a\prime ,q}$ coefficients are finite if α and β are linearly independent (i.e. the local frame is well-defined).

The result for ∂D^l_m′m/∂r_a′,q is given by inserting eqn. 36 into eqn. 24 to give

$$\frac{\partial }{\partial {\mathbf{r}}_{a\prime ,q}}{D}_{m\prime m}^l[{\mathbf{R}}_a^{-1}]={\displaystyle \sum _{t=1}^3{X}_t^{a\prime ,q}}{\displaystyle \sum _{i=-1}^1{\displaystyle \sum _{k=-1}^1{B}_{l-1,m-i}^k{C}_{lm}^i{D}_{ik}^1{[{\mathbf{M}}_t]}^{*}{D}_{m\prime ,m-i+k,}^l[{\mathbf{R}}_a^{-1}]}}.$$ (38)

The q^th component of ${\mathbf{F}}_{a\to a\prime }^{\mathit{\text{orient}}}$ is found by inserting eqn. 38 into eqn. 35 to give

$$\begin{array}{cc}{\mathbf{F}}_{a\to a\prime ,q}^{\mathit{\text{orient}}}\hfill & =-{\displaystyle \sum _{t=1}^3{X}_t^{a\prime ,q}}{\displaystyle \sum _{lm}{\phi }_{lm}^{*}{\displaystyle \sum _{ik}{B}_{l-1,m-i}^k{C}_{lm}^i{D}_{ik}^1{[{\mathbf{M}}_t]}^{*}{Q}_{l,m-i+k}^a}}\hfill \\ \hfill & ={\displaystyle \sum _{t=1}^3{X}_t^{a\prime ,q}}{\mathbf{\tau }}_{a,t}\hfill \end{array},$$ (39)

where the expression for torque (eqn. 30) has been used in the last step. This central result for orientational atomic force is expressed in terms of torque. The torque τ_a on multipole a imparts force to atoms a′ (a′ = a, N1, N2) through geometric functions $X_t^{a\prime ,q}$ which have units of inverse distance. Since ${\displaystyle {\sum }_{a\prime }{X}_t^{a\prime ,q}}=0$, the total orientational force arising from τ_a is zero, i.e.

$${\displaystyle \sum _{a\prime }{\mathbf{F}}_{a\to a\prime ,q}^{\mathit{\text{orient}}}}={\mathbf{F}}_{a\to a,q}^{\mathit{\text{orient}}}+{\mathbf{F}}_{a\to \mathrm{N}1,q}^{\mathit{\text{orient}}}+{\mathbf{F}}_{a\to \mathrm{N}2,q}^{\mathit{\text{orient}}}=0.$$ (40)

The mechanical expression for torque on atom a can be recovered by inserting eqn. 37 into 39 (see section S9 of the SI for more details), i.e.

$$\begin{array}{cc}{\mathbf{\tau }}_a\hfill & =\mathbf{\alpha }\times {\mathbf{F}}_{a\to \mathrm{N}1}^{\mathit{\text{orient}}}+\mathbf{\beta }\times {\mathbf{F}}_{a\to \mathrm{N}2}^{\mathit{\text{orient}}}\hfill \\ \hfill & ={\mathbf{r}}_{\mathrm{N}1}\times {\mathbf{F}}_{a\to \mathrm{N}1}^{\mathit{\text{orient}}}+{\mathbf{r}}_{\mathrm{N}2}\times {\mathbf{F}}_{a\to \mathrm{N}2}^{\mathit{\text{orient}}}+{\mathbf{r}}_a\times {\mathbf{F}}_{a\to a}^{\mathit{\text{orient}}}\hfill \end{array},$$ (41)

where the definitions for α and β and eqn. 40 has been used in the last step.

Total Molecular Force and Torque

The total molecular force F_tot is the total translational atomic force, since both the orientation and geometry-dependent atomic forces sum to zero (see eqns. 40 and 16). The total molecular torque with respect to the center of mass R_COM (COM) is given by

$${\mathbf{\tau }}_{\text{tot}}={\displaystyle \sum _a({\mathbf{r}}_a-{\mathbf{R}}_{\text{COM}})\times ({\mathbf{F}}_a^{trans}+{\mathbf{F}}_a^{\mathit{\text{orient}}}+{\mathbf{F}}_a^{\mathit{\text{geom}}.\mathit{\text{depend}}})}.$$ (42)

The geometry-dependent contribution to eqn. 42 is zero. This result follows from eqn. 14 and noting ∑_a r_a × ∂η/∂r _a = 0 (see section S10 of the SI for a proof). By eqns. 41 and 40, the orientation force contribution to the total molecular torque can be expressed in terms of atomic torques τ_a (eqns. 31 – 33) by

$${\mathbf{\tau }}_{\text{tot}}={\displaystyle \sum _a{\mathbf{\tau }}_a+({\mathbf{r}}_a-{\mathbf{R}}_{\text{COM}})\times {\mathbf{F}}_a^{trans}}.$$ (43)

Computational Details

The expressions for atomic forces are tested by calculating inter-molecular electrostatic energies and forces on hydrogen bonded dimers using atomic point and Gaussian multipoles fit to the ab initio electrostatic potential (ESP). The geometries of the monomers are optimized. Atomic point multipole and Slater-type contracted Gaussian multipoles are fit to the ESP calculated at the HF/6-31G* and the HF/aug-cc-pVTZ levels using methods described in our recent work³⁴. All geometry optimizations and ab initio ESP calculations are performed using the Gaussian 03 software package⁷¹.

Internal geometry derivatives of the local frame multipole moments $\partial Q_{lm\prime }^{a,Loc}/\partial {\eta }_0$ are calculated by finite difference

$$\frac{\partial Q_{lm}^{a,Loc}}{\partial {\eta }_0}=\frac{Q_{lm}^{a,Loc}({\eta }_0+h)-Q_{lm}^{a,Loc}({\eta }_0-h)}{2h},$$ (44)

where h = 0.01 Å for bond lengths and 1° for angles. The perturbed moments $Q_{lm}^{a,Loc}({\eta }_0\pm h)$ are found by perturbing the η variable on the optimized monomer geometry by ±h and calculating a new set of atomic multipoles for the perturbed geometry. For the Gaussian multipoles, the atomic Slater exponents are kept at their equilibrium geometry values during the geometric perturbations.

The dimer geometries are optimized, while keeping the monomer geometries rigid in their respective monomer-optimized geometries. Inter-molecular electrostatic energies and atomic forces calculated by the atomic multipoles are compared with their ab initio reference values. Ab initio electrostatic energies are calculated by the Reduced Variation Space^67,68 (RVS) decomposition method using the GAMESS quantum chemistry program⁷². Ab initio electrostatic forces are calculated by finite difference of RVS electrostatic energies

$${\mathbf{F}}_{a\prime ,q}^{QM}=-\left(\frac{U^{QM}({\mathbf{r}}_{a\prime ,q}+h^{QM})-U^{QM}({\mathbf{r}}_{a\prime ,q}-h^{QM})}{2h^{QM}}\right),$$ (45)

where h^QM = 10⁻³ Å. In addition, analytic multipole atomic forces are compared to numerical finite difference derivatives of atomic multipole energies by a similar expression with h^GM = 10⁻⁶ Å. Note that in the calculation of finite difference multipole forces, the local moments are re-calculated at each perturbed geometry through eqn. 9 and then rotated to the global frame through eqn. 6 with updated rotation matrices calculated from the perturbed geometries.

The internal geometry variables for bond length, bond angle, improper torsion angle, and torsion angle are chosen so that the following two conditions are satisfied: 1) the number of internal geometry variables is N_v = 3N_atom – 6, and 2) each variable can be perturbed independently of the other variables. The first condition arises because only 3N_atom – 6 variables are needed to completely specify the internal geometry of the molecule for non-linear molecules^73,74. Condition 2 is used in order that finite difference derivatives of multipole moments $Q_{lm}^{a,Loc}$ with respect to internal geometry variable (eqn. 44) can be calculated. Because of condition 2, the angle variables must be carefully chosen so that changing one angle variable will not change the other angle variables. Water is a simple example, since the two bond lengths and one bond angle constitute a set of internal variables which satisfy conditions 1 and 2. For the case of ammonia, the 3 bond lengths N-H1, N-H2, N-H3, the two bond angles θ₁ = H1-N-H2 and θ₂ = H1-N-H3, and the ω = H2-H1-N-H3 improper torsion angle satisfies conditions 1) and 2) as illustrated in Figure 2. In typical valence force fields, the internal geometry variables for ammonia are usually chosen to be the set of 3 bond lengths and 3 bond angles for symmetry reasons. Though this set of variables satisfies condition 1, it does not satisfy condition 2, i.e. if one bond angle is varied, it will change at least one other bond angle. In the SI, internal geometry variables which satisfy 1) and 2) are given for the other molecules studied in this work, such as acetone and dimethyl ether. From the examples given, it should be apparent how internal variables which satisfy conditions 1) and 2) can be chosen for an arbitrary size non-linear molecule.

Figure 2.

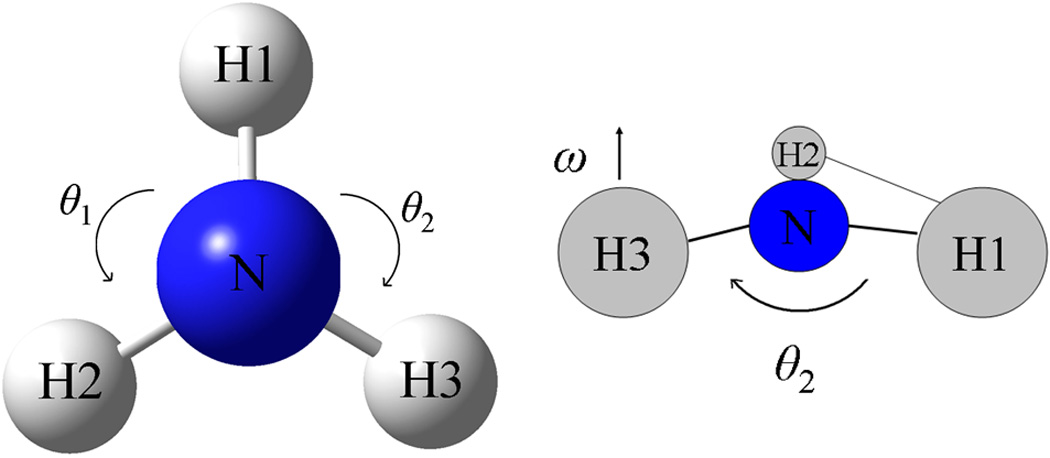
Bond angle variables for ammonia: θ₁ (H1-N-H2) and θ₂ (H1-N-H3) (left). Improper torsion angle ω (H2-H1-N-H3) (right)

Results

Intermolecular electrostatic energies and forces calculated by atomic multipole models are compared to their respective ab initio values. Following our recent work³⁴, electrostatic dimer energies calculated by ESP-fitted atomic point and Gaussian multipoles are presented for molecules hydrogen bonded to water. Atomic forces calculated by static and geometry-dependent multipoles are compared to ab initio electrostatic atomic forces. Total molecular electrostatic forces and total molecular torques calculated by static Gaussian multipoles are compared to their respective ab initio values. Lastly, the molecular multipole moment calculated by static and geometry-dependent multipoles are plotted as a function of bond angle for the case of water.

Electrostatic Energy

The electrostatic energies calculated by ESP-fitted atomic point multipole and Gaussian multipoles for hydrogen bonded dimers are compared with their respective ab initio values. In the dimer geometry, the monomers are kept at their monomer optimized geometries, and therefore, the geometry-dependent contribution to the electrostatic energy is zero. For the water-water dimer, the electrostatic energy calculated by atomic point octapoles (l_max = 3), Gaussian octapoles, and ab initio is plotted as a function of H..O distance in Figure 3. Recall that octapoles (l_max = 3) also include multipoles of lower order, i.e. monopoles, dipoles, and quadrupoles. For large H..O separations (≥ 2.5Å), the electrostatic energies calculated by both atomic point octapoles and Gaussian octapoles agree with their reference ab initio HF/6-31G* values. However, at the equilibrium H..O separation of 2.02 Å, the water-water electrostatic dimer energies are −6.53 kcal/mol for point octapoles, −7.52 kcal/mol for Gaussian octapoles, and −7.55 kcal/mol for ab initio. The under-estimation of the point octapole electrostatic energy at short range is an example of penetration error^18,39 for point multipoles.

Figure 3.

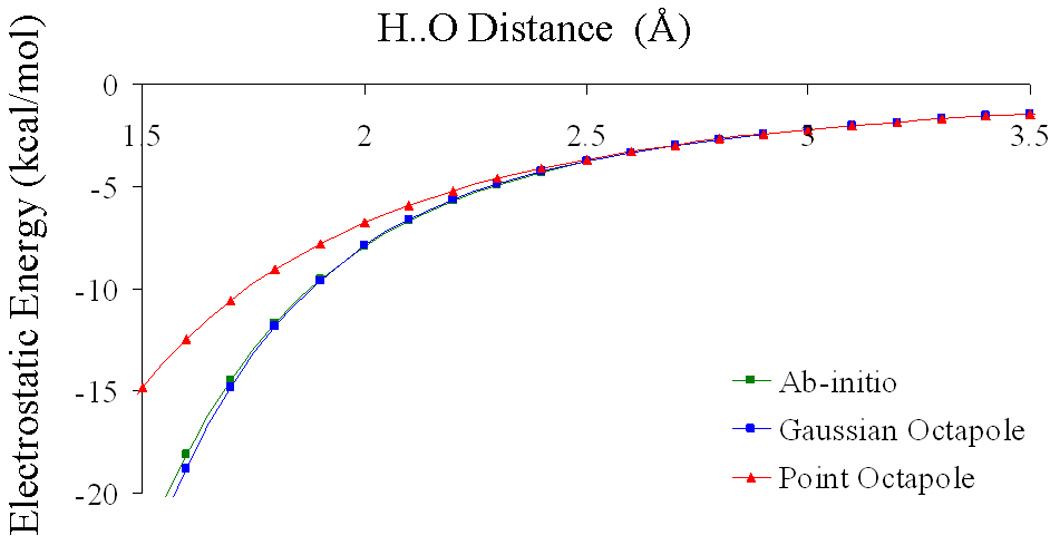
Electrostatic dimer energy for the water-water dimer as a function of H..O distance. The electrostatic energies calculated by Gaussian octapoles and point octapoles are compared to their ab initio HF/6-31G* values. The HF/6-31G* equilibrium dimer H..O distance is 2.02 Å

In Table I, the electrostatic dimer energy for various molecules hydrogen bonded to water are given at equilibrium separations. The electrostatic energy calculated by Gaussian monopoles (l_max = 0), dipoles (l_max = 1), quadrupoles (l_max = 2), octapoles (l_max = 3), and hexadecapoles (l_max = 4) are compared to their ab initio HF/6-31G* reference values. In general, there is a significant improvement in going from Gaussian monopoles to Gaussian quadrupoles. For example, the electrostatic dimer energies for the ammonia-water dimer are −8.59, −9.13, and −9.98 kcal/mol for Gaussian monopoles, dipoles, and quadrupoles, respectively. These values can be compared to the ab initio electrostatic dimer energy of −10.03 kcal/mol. On average, there is a small improvement for energy in going from Gaussian quadrupoles to hexadecapoles. For this small set of hydrogen bonded dimers, the root mean square deviations (rmsd) in electrostatic dimer are 0.713, 0.734, 0.140, 0.117, and 0.078 kcal/mol for Gaussian monopoles, dipoles, quadrupoles, octapoles, and hexadecapoles. Additional results, including electrostatic energies calculated by HF/aug-cc-pVTZ Gaussian multipoles, can be found in the SI.

Table I.

Electrostatic Energy (kcal/mol) for Water Hydrogen Bonded Dimers At Equilibrium Separation.

X	Mono.a	Dip.	Quad.	Oct.	Hex.	RVS
Water	−6.845	−7.074	−7.502	−7.520	−7.542	−7.546
Methanol	−7.172	−6.735	−7.238	−7.257	−7.285	−7.265
Formamide	−11.35	−11.18	−11.75	−11.78	−11.86	−11.98
Ammonia	−8.594	−9.130	−9.982	−10.06	−10.07	−10.03
Acetylaldehyde	−6.808	−6.221	−6.849	−6.879	−6.922	−7.022
Dimethyl Ether	−5.791	−6.438	−6.744	−6.828	−6.840	−6.787
rmsd	0.713	0.734	0.140	0.117	0.078

^aGaussian monopoles, dipoles, quadrupoles, octapoles, and hexadecapoles fit to the HF/6-31G* ESP are compared to the reference ab initio RVS values.

Electrostatic Atomic Force

Atomic forces calculated by static and geometry-dependent atomic point and Gaussian multipoles are compared with their ab initio values. As a first test, the analytic and numerical finite difference atomic forces calculated by geometry-dependent Gaussian hexadecapoles on an oxygen atom in the water-water dimer are given in Table II. The analytic and numerical atomic forces agree to a precision of 10⁻⁷. In Table III, the atomic electrostatic forces on an oxygen atom in the water-water dimer calculated by static and geometry-dependent multipole models are compared with their respective ab initio atomic electrostatic forces. At the equilibrium water-water dimer geometry (H..O distance = 2.02 Å), the atomic forces for Gaussian octapoles are given, while the forces for atomic point octapoles are calculated when the waters are separated by a longer distance (H..O distance = 3.0 Å). In both cases, the atomic forces calculated by geometry-dependent multipole models are comparable with their ab initio atomic forces, while there is a significant discrepancy for the atomic forces calculated by static multipoles. For example, the y-component of force on oxygen F_y at the equilibrium separation is 0.247 kcal/mol/Å for static Gaussian octapoles and 4.504 for geometry-dependent Gaussian octapoles. These values can be compared to the ab initio result for F_y of 4.972 kcal/mol/Å. The rmsd errors in atomic force over all atoms in the dimer is 1.567 and 0.147 kcal/mol/Å for static and geometry-dependent Gaussian octapoles, respectively.

Table II.

Analytical and Numerical Finite Difference Forces^a (kcal/mol/Å)

	Fx	Fy	Fz
Analytic	−1.3664760	4.5198024	−0.0044384
Numerical	−1.3664758	4.5198024	−0.0044383

^aAtomic forces on an oxygen atom in a water – water dimer calculated by geometry-dependent HF/6-31G* Gaussian hexadecapoles.

Table III.

Comparison of Multipole Electrostatic Forces^a (kcal/mol/Å) with Ab initio

	Fx	Fy	Fz	rmsdd
Gauss. Oct. (Static)b	−1.390	0.247	−0.004	1.567
Gauss. Oct. (Geom. Depend.)	−1.351	4.504	−0.004	0.147
Ab initio	−1.543	4.972	−0.004
Point Oct. (Static)c	−1.358	2.614	0.000	0.620
Point Oct. (Geom. Depend.)	−0.485	1.438	0.000	0.019
Ab initio	−0.498	1.452	0.000

^aAtomic forces evaluated on an oxygen atom in the water – water dimer.

^bGaussian octapole atomic forces are evaluated at the equilibrium dimer distance with an H..O distance of 2.02 Å.

^cPoint octapole atomic forces are evaluated at the water-water dimer geometry with an H..O distance of 3.0 Å.

^dThe rmsd is the average error in electrostatic atomic forces over all atoms.

The results given above for the water-water dimer are indicative of the other cases studied. In Table IV, the rmsd errors in atomic forces with respect to ab initio are given for hydrogen bonded dimers calculated by static and geometry-dependent Gaussian dipoles, quadrupoles, octapoles, and hexadecapoles. In all cases, there is a significant improvement in going from static to geometry-dependent models. The rmsd errors (kcal/mol/Å) averaged over all dimers is 1.216, 0.369, 0.143, and 0.148 for geometry-dependent Gaussian dipoles, quadrupoles, octapoles, and hexadecapoles, respectively. Additional results, including atomic forces calculated by HF/aug-cc-pVTZ Gaussian multipoles, can be found in the SI.

Table IV.

Rmsd Error^a in Intermolecular Electrostatic Atomic Forces (kcal/mol/Å) for Water Hydrogen bonded Dimers.

X	Geometry-Dependent				Static
	Dip.	Quad.	Oct.	Hex.	Dip.	Quad.	Oct.	Hex.
Water	1.287	0.449	0.147	0.155	3.913	1.634	1.567	0.991
Methanol	1.089	0.381	0.135	0.149	2.734	1.543	1.450	1.030
Formamide	1.239	0.315	0.168	0.135	4.239	4.346	3.354	2.722
Ammonia	1.660	0.446	0.153	0.203	4.849	2.137	2.000	1.432
Acetylaldehyde	1.011	0.312	0.127	0.122	2.266	2.792	2.837	1.758
Dimethyl Ether	0.917	0.331	0.122	0.129	1.845	1.406	2.162	2.188
Average	1.216	0.369	0.143	0.148	3.378	2.541	2.341	1.615

^aError is calculated with respect to reference HF/6-31G* atomic forces.

Total Molecular Force and Torque

The total molecular force F_tot and total molecular torque τ_tot on a methanol molecule in a methanol-water dimer are calculated by Gaussian quadrupoles and compared to their reference HF/6-31G* values in Table V and Table VI, respectively. The results for F_tot and τ_tot calculated by Gaussian quadrupoles are comparable with their reference ab initio values. For example, the x component of F_tot (kcal/mol/Å) is −12.90 for Gaussian quadrupoles and −12.57 for ab initio. The rmsd errors in F_tot and τ_tot with respect to ab initio are 0.193 kcal/mol/Å and 0.081 kcal/mol, respectively. Similar results are obtained for the other hydrogen bonded dimers (see the SI for more details). Since the geometry-dependent contribution to both F_tot and τ_tot are zero (at the equilibrium monomer geometries), the results for F_tot and τ_tot calculated by static and geometry-dependent multipole models are identical. Thus, both static and geometry-dependent multipole models are capable of reproducing total molecular forces and torques. Additional results, including molecular forces and torques calculated by HF/aug-cc-pVTZ Gaussian multipoles, can be found in the SI.

Table V.

Total Molecular Force on Methanol in a Methanol-Water Dimer^a (kcal/mol/Å)

	Fx	Fy	Fz
Gauss. Quad.	−12.897	−3.580	0.866
Ab initio	−12.569	−3.518	0.880

^aCalculated by HF/6-31G* Gaussian quadrupoles. The rmsd error in total molecular force is 0.193 kcal/mol/Å

Table VI.

Total Molecular Torque on Methanol in a Methanol-Water Dimer^a (kcal/mol)

	Fx	Fy	Fz
Gauss. Quad.	0.243	1.223	9.082
Ab initio	0.244	1.258	8.904

^aTorque is calculated with respect to the COM by HF/6-31G* Gaussian quadrupoles. The rmsd error in total molecular torque is 0.081 kcal/mol.

Molecular Multipole Moment Geometry-Dependence

The molecular dipole moment of water is plotted as a function of bond angle in Figure 4. The molecular dipole calculated by static and geometry-dependent Gaussian dipoles are compared to their reference HF/6-31G* values. At the equilibrium geometry, both static and geometry-dependent Gaussian dipoles reproduce the molecular dipole moment for water. As the bond angle increases, the molecular dipole of water decreases. However, static dipoles significantly overestimate the amount by which the molecular dipole decreases. For example, at a bond angle of 111°, the HF/6-31G* dipole moment (D) of water is 2.099 D. This value can be compared to the values predicted by static Gaussian dipoles of 1.971 D and geometry-dependent Gaussian dipoles of 2.096 D. Similar results are obtained for higher order molecular multipole moments calculated by static and geometry-dependent Gaussian monopoles, dipoles, and quadrupoles, (See the SI for more details).

Figure 4.

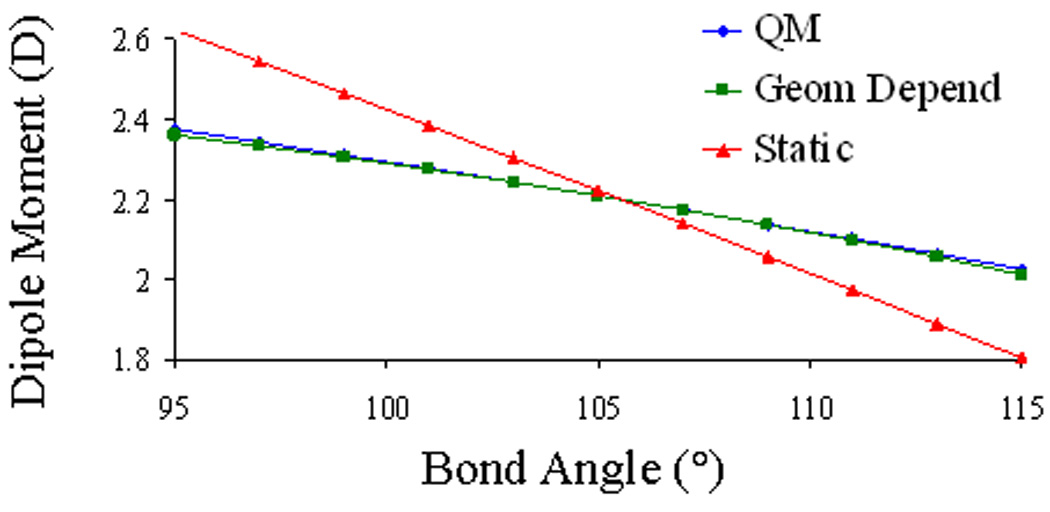
Molecular dipole moment of water as a function of bond angle for static Gaussian dipoles, geometry-dependent Gaussian dipoles, and the reference HF/6-31G* values. The HF/6-31G* equilibrium bond angle for water is 105.0°

Conclusions

Atomic force expressions are found for geometry-dependent atomic point multipole and Gaussian multipole models for use in simulations of flexible molecules. The multipolar forces are tested by comparing to numerical finite difference derivatives of multipolar energy. In addition, the multipolar energies and atomic forces are compared to ab initio electrostatic energies and forces. In contrast to static multipoles, it is shown that geometry-dependent multipoles are comparable with ab initio electrostatic atomic forces. However, both static and geometry-dependent models are able to reproduce total molecular forces and total molecular torques. Another advantage of using geometry-dependent multipole models over static multipole models is that electrostatic interactions can be accounted for over a range of intra-molecular geometries for flexible molecules. For example, geometry-dependent models are able to accurately account for the ab initio molecular multipole moments as a function bond length and bond angle for the case of water. In the present study, the geometry-dependent multipoles are represented by expanding the local frame multipole moments $Q_{lm}^{a,Loc}(\eta )$ as a truncated linear Taylor series in internal geometry variables η (bond lengths, bond angles, etc.) about equilibrium geometry values. However, the expressions for atomic multipole force can be used in other functional forms of $Q_{lm}^{a,Loc}(\eta )$ (e.g. higher order Taylor series and/or a Fourier series for dihedral angles).

In order to arrive at the result for orientational force, a general expression for Wigner rotation matrix derivatives ∂D^l_m′m/∂Ω for arbitrary Ω is proposed. The general result for ∂D^l_m′m/∂Ω is applied to the special cases when Ω represents an infinitesimal rotation, an Euler angle, and a quaternion in the SI. For the special cases when Ω is an Euler angle or infinitesimal rotation, the results for ∂D^l_m′m/∂Ω agree with those given by Varshalovich⁵³ et al. By letting Ω be an atomic position, an expression for ∂D^l_m′m/∂r_{a ’,q} is evaluated and used to find a compact equation for atomic orientational force, which does not contain the singularity problems associated with a procedure based on Euler angles.

Appendix: Mathematical Background

In this section, background information needed in the derivation of ∂D^l_m′m/∂Ω is given. Properties of spherical harmonics⁶⁹,⁷⁰ and Wigner functions⁵³–⁵⁷ are summarized. This is followed by a brief summary of Cartesian rotation matrix derivatives (∂R/∂Ω)R⁻¹.

Spherical Harmonics

The complex spherical harmonics Y_lm (θ,φ) ≡ Y_lm (r̂) are functions on a unit sphere which can be defined in terms of Associated Legendre functions P_lm(cos θ) by

$$Y_{lm}(\theta ,\phi )\equiv {(-1)}^m\sqrt{\frac{2l+1}{4\pi }}\sqrt{\frac{(l-m)!}{(l+m)!}}{P}_{lm}(\text{cos}\theta )e^{im\phi }.$$ (A.1)

Many useful properties of Associated Legendre functions and spherical harmonics can be found in Arfken⁷⁰. An especially useful result can be found in Hobson⁶⁹, in which P_lm(cos θ) is expressed as a homogeneous polynomial of degree l in sin θ and cos θ for 0 ≤ m ≤ l

$$P_{lm}(\text{cos}\theta )=\frac{(l+m)!}{2^m}{\displaystyle \sum _{k=0}^{\left[\frac{l-m}{2}\right]}{\left(\frac{-1}{4}\right)}^k\frac{{\text{cos}}^{l-m-2k}\theta {\text{ sin}}^{m+2k}\theta }{(l-m-2k)!(m+k)!k!}}.$$ (A.2)

This result can be used to express spherical harmonics as a homogeneous polynomial in terms of a new set of variables ξ ≡ (ξ₋₁, ξ₀, ξ₊₁) by

$$Y_{lm}(\mathbf{\xi })=\sqrt{\frac{2l+1}{4\pi }}\frac{\sqrt{(l+m)!(l-m)!}}{2^{m/2}}{\displaystyle \sum _{k=0}^{\left[\frac{l-m}{2}\right]}{\left(\frac{1}{2}\right)}^k\frac{{{\xi }_0}^{l-m-2k}{{\xi }_1}^{m+k}{{\xi }_{-1}}^k}{(l-m-2k)!(m+k)!k!}}$$ (A.3)

where

$$\begin{array}{ccc}{\xi }_{-1}\equiv \frac{\text{sin}\theta }{\sqrt{2}}{\mathrm{e}}^{-i\phi }=\frac{x-iy}{\sqrt{2}r},\hfill & {\xi }_0\equiv \text{cos}\theta =\frac{z}{r},\hfill & {\xi }_{+1}\equiv -\frac{\text{sin}\theta }{\sqrt{2}}{\mathrm{e}}^{\mathrm{i}\phi }=-\frac{x+iy}{\sqrt{2}r}\hfill \end{array}$$ (A.4)

which satisfy ξ₀² – 2ξ₁ξ₋₁ = 1 on a unit sphere. It is straightforward to evaluate eqn. A.3 for l = 1

$$\begin{array}{ccc}{Y}_{11}(\mathbf{\xi })=\sqrt{\frac{3}{4\pi }}{\xi }_1,\hfill & Y_{10}(\mathbf{\xi })=\sqrt{\frac{3}{4\pi }}{\xi }_0,\hfill & Y_{1,-1}(\mathbf{\xi })=\sqrt{\frac{3}{4\pi }}{\xi }_{-1}\hfill \end{array}.$$ (A.5)

In terms of the new variables, recurrence relations⁷⁰ for spherical harmonics can be expressed as

$${\xi }_i{Y}_{lm}(\mathbf{\xi })=A_{lm}^i{Y}_{l-1,m+i}(\mathbf{\xi })+B_{lm}^i{Y}_{l+1,m+i}(\mathbf{\xi }).$$ (A.6)

where $A_{lm}^i$ and $B_{lm}^i$ are defined to be non-zero for i = −1, 0, 1 and |m| ≤ l by

$$A_{lm}^{\pm 1}\equiv -\sqrt{\frac{(l\mp m)(l\mp m-1)}{2(2l-1)(2l+1)}},A_{lm}^0\equiv \sqrt{\frac{(l+m)(l-m)}{(2l-1)(2l+1)}},$$ (A.7)

$$B_{lm}^{\pm 1}\equiv \sqrt{\frac{(l\pm m+1)(l\pm m+2)}{2(2l+1)(2l+3)}},B_{lm}^0\equiv \sqrt{\frac{(l+m+1)(l-m+1)}{(2l+1)(2l+3)}}.$$ (A.8)

Since Y_lm is a homogeneous polynomial of degree l in terms of ξ ≡ (ξ₋₁, ξ₀, ξ₊₁), the derivative of Y_lm with respect to ξi is a polynomial of degree l – 1. Through the polynomial expression in eqn. A.3, it is straightforward to verify the following relationship for derivatives of Y_lm for all complex values of ξi

$$\frac{\partial Y_{lm}}{\partial {\xi }_i}=C_{lm}^i{Y}_{l-1,m-i},$$ (A.9)

where $C_{lm}^i$ is defined to be non-zero for i = −1, 0, 1 and |m| ≤ l by

$$\begin{array}{cc}{C}_{lm}^{\pm 1}\equiv \sqrt{\frac{2l+1}{2l-1}}\sqrt{\frac{(l\pm m)(l\pm m-1)}{2}},\hfill & C_{lm}^0\equiv \sqrt{\frac{2l+1}{2l-1}}\sqrt{(l+m)(l-m)}\hfill \end{array}.$$ (A.10)

Wigner Rotation Matrices

Spherical harmonics transform under rotations through Wigner⁵³–⁵⁷ functions D^l_m′m. If r̂ = (sin θ cos φ, sin θ sinφ, cosθ) is a point on a unit sphere and R is a Cartesian rotation matrix,

$$Y_{lm}({\mathbf{R}}^{-1}\widehat{r})={\displaystyle \sum _{m\prime =-l}^l{D}_{m\prime m}^l[\mathbf{R}]Y_{lm\prime }(\widehat{r})}$$ (A.11)

Since spherical harmonics are orthonormal when integrated over a unit sphere, the Wigner rotation matrices can be represented by the following integral over a unit sphere

$$D_{m\prime m}^l[\mathbf{R}]={\displaystyle \int d\widehat{r}{Y}_{lm\prime }^{*}(\widehat{r})Y_{lm}({\mathbf{R}}^{-1}\widehat{r})}.$$ (A.12)

Note that D^l_m′m[R] is unitary and satisfies

$$D_{m\prime m}^l[{\mathbf{R}}^{-1}]=D_{mm\prime }^l{[\mathbf{R}]}^{*}.$$ (A.13)

Recursion formulae⁵³,⁵⁷ have been developed to evaluate D^l_m′m[R]. For l = 1, D¹ can be expressed as a unitary transformation of R by

$${\mathbf{D}}^1=\mathbf{F}+i\mathbf{G},$$ (A.14)

$$\left(\begin{array}{ccc}{\mathbf{F}}_{-1,-1}& {\mathbf{F}}_{-1,0}& {\mathbf{F}}_{-1,1}\\ {\mathbf{F}}_{0,-1}& {\mathbf{F}}_{0,0}& {\mathbf{F}}_{0,1}\\ {\mathbf{F}}_{1,-1}& {\mathbf{F}}_{1,0}& {\mathbf{F}}_{1,1}\end{array}\right)\equiv \left(\begin{array}{ccc}\frac{{\mathbf{R}}_{11}+{\mathbf{R}}_{22}}{2}& \frac{{\mathbf{R}}_{13}}{\sqrt{2}}& \frac{{\mathbf{R}}_{22}-{\mathbf{R}}_{11}}{2}\\ \frac{{\mathbf{R}}_{31}}{\sqrt{2}}& {\mathbf{R}}_{33}& -\frac{{\mathbf{R}}_{31}}{\sqrt{2}}\\ \frac{{\mathbf{R}}_{22}-{\mathrm{R}}_{11}}{2}& -\frac{{\mathbf{R}}_{13}}{\sqrt{2}}& \frac{{\mathbf{R}}_{11}+{\mathbf{R}}_{22}}{2}\end{array}\right),$$ (A.15)

$$\left(\begin{array}{ccc}{\mathbf{G}}_{-1,-1}& {\mathbf{G}}_{-1,0}& {\mathbf{G}}_{-1,1}\\ {\mathbf{G}}_{0,-1}& {\mathbf{G}}_{0,0}& {\mathbf{G}}_{0,1}\\ {\mathbf{G}}_{1,-1}& {\mathbf{G}}_{1,0}& {\mathbf{G}}_{1,1}\end{array}\right)\equiv \left(\begin{array}{ccc}\frac{{\mathbf{R}}_{21}-{\mathbf{R}}_{12}}{2}& \frac{{\mathbf{R}}_{23}}{\sqrt{2}}& -\frac{{\mathbf{R}}_{12}+{\mathbf{R}}_{21}}{2}\\ -\frac{{\mathbf{R}}_{32}}{\sqrt{2}}& 0& -\frac{{\mathbf{R}}_{32}}{\sqrt{2}}\\ \frac{{\mathbf{R}}_{12}+{\mathbf{R}}_{21}}{2}& \frac{{\mathbf{R}}_{23}}{\sqrt{2}}& \frac{{\mathbf{R}}_{12}-{\mathbf{R}}_{21}}{2}\end{array}\right).$$ (A.16)

For l ≥ 2, D^l_m′m[R] can be evaluated by the following three recursion expressions

$$B_{lm-i}^i{D}_{m\prime ,m}^{l+1}={\displaystyle \sum _{j=-1}^1{D}_{ji}^1[\mathbf{R}]D_{m\prime -j,m-i}^l[\mathbf{R}]B_{lm\prime -j}^j},$$ (A.17)

where $B_{lm-i}^i$ is nonzero for i = −1, 0, 1 and |m − i| ≤ l by eqn. A.7. The recursion relationships 5.9, 5.1, and 5.14 from Choi et al.⁵⁷ correspond to i = −1, 0, 1, respectively.

Cartesian Rotation Matrix Derivatives

The general expression for ∂D^l_m′m/∂Ω assumes the corresponding Cartesian rotation matrix derivative A^Ω ≡ (∂R/∂Ω)R⁻¹ is given. Since this result is needed, a brief discussion is given for the rotation derivative of a Cartesian vector ν. Suppose a Cartesian rotation matrix R which transforms a vector ν′ to ν, i.e. ν = Rν′. If R is a function of one or more rotation variables Ω (e.g. an Euler angle, quaternion, atomic position, etc.), then ν also becomes a function of Ω, i.e. ν(Ω) = R(Ω)ν′. Since ν′ = R⁻¹ν, derivatives of ν with respect to Ω can be expressed as a linear transformation of ν as

$$\frac{\partial \mathbf{\nu }}{\partial \mathrm{\Omega }}=\frac{\partial \mathbf{R}}{\partial \mathrm{\Omega }}\mathbf{\nu }\prime ={\mathbf{A}}^{\mathrm{\Omega }}\mathbf{\nu }.$$ (A.18)

For many cases, A^Ω is an antisymmetric matrix (e.g. Ω is an Euler angle, rotation about a coordinate axis). In particular, the A^Ω matrices for torque and orientational force are antisymmetric. For more discussion on this point, see section S2 in the SI.