SHAPE-Directed RNA Secondary Structure Prediction

Abstract

The diverse functional roles of RNA are determined by its underlying structure. Accurate and comprehensive knowledge of RNA structure would inform a broader understanding of RNA biology and facilitate exploiting RNA as a biotechnological tool and therapeutic target. Determining the pattern of base pairing, or secondary structure, of RNA is a first step in these endeavors. Advances in experimental, computational, and comparative analysis approaches for analyzing secondary structure have yielded accurate structures for many small RNAs, but only a few large (>500 nts) RNAs. In addition, most current methods for determining a secondary structure require considerable effort, analytical expertise, and technical ingenuity. In this review, we outline an efficient strategy for developing accurate secondary structure models for RNAs of arbitrary length. This approach melds structural information obtained using SHAPE chemistry with structure prediction using nearest-neighbor rules and the dynamic programming algorithm implemented in the RNAstructure program. Prediction accuracies reach ≥95% for RNAs on the kilobase scale. This approach facilitates both development of new models and refinement of existing RNA structure models, which we illustrate using the Gag-Pol frameshift element in an HIV-1 M-group genome. Most promisingly, integrated experimental and computational refinement brings closer the ultimate goal of efficiently and accurately establishing the secondary structure for any RNA sequence.

1. Introduction

RNA is a uniquely versatile macromolecule with diverse functions. In addition to its classically understood role as the intermediary between genome and proteome, RNA plays direct roles in fundamental cellular processes including biological catalysis, gene regulation and host defense. RNA also serves as the genome for many viruses. All of these functions depend on, or are modulated by, the ability of RNA to fold into higher order structures. Accurate models for the underlying structure are therefore critical for proposing and confirming hypotheses regarding RNA function.

Determining the complete three-dimensional (termed the tertiary) structure is the ultimate goal for many RNAs. However, only limited sets of RNAs are candidates for current high resolution crystallography and NMR approaches. A simpler problem is to determine the base pairing pattern (termed the secondary structure) of an RNA. Secondary structure determination, independent of higher order structural information, is possible because the hydrogen bonding and stacking interactions that collectively form secondary structure are usually stronger than tertiary interactions [1-4], and because RNA folding is often hierarchical [5, 6], with many secondary structural motifs forming prior to tertiary contacts. Additionally, knowledge of the secondary structure greatly restricts possible three-dimensional conformations and facilitates tertiary structure prediction [7-9]. Moreover, a subset of RNA functions may depend more directly on secondary structural motifs than on global folds.

Insight into the secondary structure can be gleaned using computer-based predictions performed using the sequence alone, or in combination with sequence alignment information or experimental data. Sequence-based folding generally includes two main elements: an energy function based on experimentally derived thermodynamic parameters, and an algorithm that explores the conformational space available to the RNA and ranks computed structures. Most energy functions use the Turner et al. [10, 11] set of nearest neighbor parameters, derived from optical melting experiments. A summary of these parameters is available at the Nearest-Neighbor Database [12]. Exploring conformational space is challenging because of the vast number of possible secondary structures, which is estimated to scale exponentially as ~1.8^N, where N is the number of nucleotides in the RNA [13]. This means that a “brute force” approach that samples every possible conformation is impossible both from a computational standpoint and from the perspective of efficient RNA folding in vivo. Consequently, the intrinsic thermodynamics and kinetics of RNA folding must conspire to restrict the folding pathway to a narrow subset of these structures, only one (or perhaps a few) of which is likely to dominate the equilibrium ensemble. Especially for short RNAs, thermodynamic considerations are likely paramount and thus the structure with the lowest free energy is the biologically active one.

1.1 Dynamic Programming Algorithms for RNA Secondary Structure Prediction

Programs based on the Zuker dynamic programming algorithm [14, 15] are widely used to search for the minimum free energy structure [16-22]. These algorithms are deterministic, meaning that given a defined set of energy rules, they always find the lowest free energy structure. The Zuker algorithm scales as O(N³) in time, where N is the number of nucleotides in the sequence. This means that doubling the sequence length requires eight times as much time to predict the structure. Nevertheless, on modern computers, the time to make a prediction is reasonably fast. The guarantee that the optimal structure can be computed and the relative computational efficiency are made possible, first, by incorporating simplifying assumptions into the energy function, and second, by limiting the types of allowed RNA folds.

The total energy is assumed to be a simple sum over all energetic components that characterize local structural elements. Two features primarily contribute to the total energy: negative (favorable) free energies arising from stabilizing base stacking and hydrogen bonding interactions in and adjacent to helices, and positive (unfavorable) free energies arising from the entropic cost of restricting conformational freedom in loops. Helix energy terms are sequence-dependent, reflect the energetic bonus of adding a base pair to a helix, and implicitly include both canonical hydrogen bonding and base stacking. These terms depend solely on interactions involving adjacent base pairs or interactions at the ends of helices. This local interaction model is termed the nearest-neighbor approximation [23].

The dynamic programming algorithm calculates the energy of the lowest free energy structure (but does not compute the complete structure itself) for all possible subsequences of an RNA. This approach is efficient because the solution for each subsequence is computed from solutions for pre-computed smaller subsequences, allowing the energies for each structural element to be computed only once. The results are stored in triangular N × N arrays whose elements i,j represent the optimal folding energy for an RNA subsequence from nucleotide i to nucleotide j. The structure for the entire RNA sequence is obtained by tracing a structure through an optimal combination of component subsequences in the array [24].

Thermodynamics-based dynamic programming algorithms have several limitations. First, computing the minimum free energy structure in a relatively efficient O(N³) manner excludes consideration of non-nested topologies. These include the biologically important case of pseudoknots, in which a loop in one helix forms the stem of another helix. Second, the assumption that the minimum free energy structure is the biologically active one may not always hold for larger RNAs, where folding kinetics may play a prominent role. Third, the biologically relevant ensemble may be dominated by several interconverting states, making a single structural model inadequate. Finally, incomplete thermodynamic rules and the simplifications inherent in the nearest neighbor model introduce uncertainty to the energy calculations.

The net effect of these limitations is that the current best-performing algorithms achieve prediction accuracies of 50-70% [11, 25-29]. Accuracies tend to be especially poor for larger RNAs. For example, for Escherichia coli 16S rRNA, which is probably the most thoroughly studied large RNA, the prediction accuracy based on sequence alone is less than 50% [26, 30].

1.2 Comparative Sequence Analysis

One way of overcoming these limitations is to use information from RNA sequence alignments [31-33]. Termed comparative sequence or covariation analysis, this approach is grounded in the principle that homologous RNAs have secondary structures that are much more conserved than their primary sequences. An alignment of homologous RNAs is used to propose base pairing interactions based on patterns of sequence variation, assuming a common consensus secondary structure. Candidate base pairs are favored or disfavored depending on whether sequence variations tend to maintain canonical base pairing or tend to occur independently, respectively.

A model with good covariation support commands strong confidence in its accuracy and such models are often the gold standard in the absence of crystallographic models. However, comparative sequence analysis cannot be applied to many RNAs of interest because the method requires multiple divergent sequences with a common secondary structure. The sequences must be similar enough to admit a multiple sequence alignment, yet divergent enough to show sufficient variation. Sequences corresponding to open reading frames are especially recalcitrant to analysis because selective pressure at the protein coding level further restricts the degree of variation. Finally, constructing a model from a sequence alignment is an iterative process that requires considerable user effort and skill.

1.3 Incorporating Experimental Data

In cases where comparative analysis is of limited use, significant improvements to RNA secondary structure prediction can be achieved when computer predictions are constrained by experimental data derived from structure-sensitive enzymatic cleavage and chemical probing reagents [11, 34, 35]. However, the net improvement gained from using traditional reagents is often modest. First, traditional reagents tend to react with only a subset of nucleotides, so the absence of reactivity cannot usually be taken as evidence for likely base pairing. Second, different reagents are required to react with all four RNA nucleotides and some of the more useful reagents, like dimethyl sulfate (DMS), react at different base functional groups depending on the nucleotide. Third, the dynamic range for many reagents is low, making it difficult to distinguish levels of reactivity beyond a qualitative “low,” “medium,” and “high” scale. Finally, while alternative chemistries such as in-line probing [36] and hydroxyl radical footprinting [37] provide valuable insight into higher order structures and react broadly with all four RNA nucleotides, they less directly report the intrinsic nucleotide flexibilities that largely characterize secondary structure. Thus, it is challenging to create quantitative relationships between reagent reactivity and RNA secondary structure.

1.4 Towards Accurate SHAPE-Directed Secondary Structure Prediction

Selective 2′-Hydroxyl Acylation analyzed by Primer Extension (SHAPE) [38, 39] chemical probing technology largely addresses these challenges. SHAPE yields quantitative reactivity information for nearly every nucleotide in an RNA. Advantageously, SHAPE is not limited by RNA size and is remarkably insensitive to solvent accessibility [38, 40, 41]. Additionally, SHAPE can be applied to both in vitro transcripts and also to RNAs from native-like cellular and viral environments. Combining SHAPE information with a thermodynamics-based dynamic programming algorithm, as implemented in RNAstructure [11], results in highly accurate secondary structure models [30]. This approach has been benchmarked and shown to yield secondary structures for diverse RNAs, including the E. coli 16S rRNA (1542 nucleotides), with >95% accuracy as judged by sensitivity (percentage of known base pairs predicted correctly) and positive predictive value (PPV, percentage of predicted base pairs in the known structure) [30] (Table 1). SHAPE has been used to propose experimentally-informed secondary structural models for many RNAs and RNA states whose structures are unlikely to be determinable by covariation or high resolution experimental approaches [30, 39, 41-57]. In this work, we will briefly review the SHAPE experimental protocol and data processing steps. We will then describe in detail how SHAPE experimental information is incorporated into a nearest neighbor dynamic programming algorithm to create accurate secondary structure models. We close with an analysis of a novel SHAPE-supported model for the HIV-1 frameshift element.

Table 1.

RNA secondary structure prediction accuracies for folding calculations performed without and with SHAPE constraints

RNA	Size (nts)	No constraints		with SHAPE
		Sensitivity	PPV	Sensitivity	PPV
Yeast tRNAAsp	75	95	95	100	100
HCV IRES domain II	95	57	59	96	100
B. subtilis RNase P,  specificity domain	154	53	51	75	83
T. thermophila group I intron,  P546 domain	155	43	44	96	98
E. coli 16S rRNA	1542	50	46	97	95

Sensitivity and PPV are the percentage of known base pairs predicted correctly and the percentage of predicted base pairs in the known structure, respectively. Calculations were performed using RNAstructure [11]. Accuracies for SHAPE-constrained structures are typically ≥95%. However, accuracy for the RNase Pspecificity domain is significantly lower, likely because many base pairs in this RNA only form in concert with the tertiary structure [62]. Data are from refs. [30, 62].

2.1 Overview of SHAPE Technology

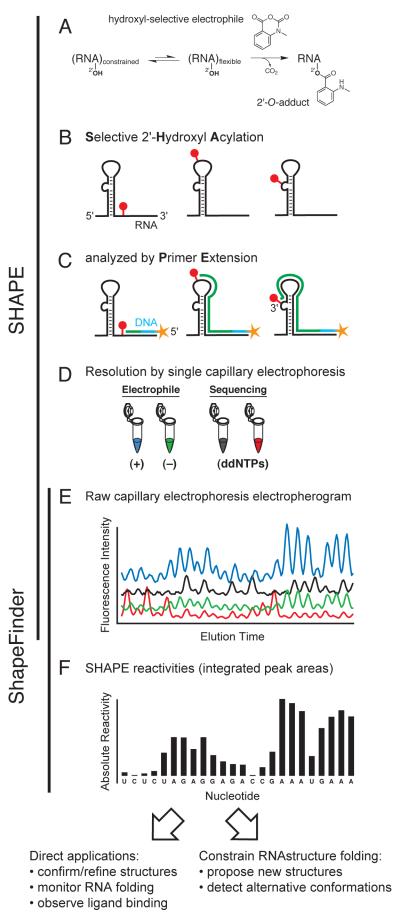
SHAPE technology involves covalently modifying RNA in a structure-dependent manner (selective 2′-hydroxyl acylation), followed by detecting the sites of modification by primer extension (original protocols described in [58, 59]). The RNA modification involves the nucleophilic attack of the 2′-hydroxyl group of the RNA ribose moiety on an electrophilic SHAPE reagent to form a 2′-O-adduct (Fig. 1A) [38]. This reaction occurs more readily with conformationally unconstrained or flexible nucleotides such as those in single stranded regions, loops, or bulges (spheres, Fig. 1B). Flexible nucleotides react preferentially because they more readily sample conformations conducive to nucleophilic attack. In contrast, nucleotides in highly structured regions are conformationally constrained and less frequently achieve an optimal geometry, making them less reactive towards SHAPE reagents. In general, solvent inaccessible, but unconstrained, nucleotides are still reactive by SHAPE.

Figure 1.

Overview of the SHAPE experimental and data analysis steps. Adapted from ref. [60].

Following modification of the RNA, modified positions are detected by primer extension using end-labeled, target-specific primers and a thermostable reverse transcriptase (Fig. 1C). Since the reverse transcriptase enzyme cannot proceed past 2′-O-modified sites in RNA, the lengths of the resulting cDNA products correspond to the distance between the primer binding and 2′-O-adduct sites. Due to differential modification of structured versus unstructured nucleotides, the frequency of producing a given cDNA product reflects the underlying RNA structure. Comparison with dideoxy nucleotide sequencing ladders allows each SHAPE reagent-dependent peak to be matched with the corresponding nucleotide position (Fig. 1D).

SHAPE technology can be implemented in an efficient and high-throughput way by automated capillary electrophoresis using DNA sequencing instruments (Fig. 1E). The capillary electrophoresis data are analyzed using the software program ShapeFinder [60]. ShapeFinder processes these data to yield normalized SHAPE reactivity values (Fig. 1F). These reactivities can be converted to ΔG_SHAPE pseudo-free energy terms and used with the energy function in the RNAstructure program to yield, generally highly accurate, secondary structure models for RNA (Table 1, and see section 3.1 below) [11, 30].

2.2 SHAPE Experimental Protocol

The experimental component of a SHAPE analysis has been recently reviewed in detail [59, 61]. Briefly, RNA is modified in a structure-selective way using an electrophilic SHAPE reagent. While SHAPE has been most commonly performed on in vitro RNA transcripts or RNAs extracted from biological environments, SHAPE reagents readily cross biological membranes and, for example, react with RNAs inside authentic HIV-1 particles [39].

Approximately 2 pmol of RNA is needed in each primer extension reaction to obtain adequate signal intensity in the capillary electrophoresis detection step, using commercially available instruments. We routinely achieve read lengths of 300 – 650 nucleotides in each primer extension reaction [50, 60]. For longer RNAs, information obtained from multiple primers, with overlapping read windows, can be combined to create datasets spanning arbitrarily long lengths [30, 39, 41].

To maintain a native-like conformation, the RNA must be renatured (in vitro transcripts) or maintained (RNAs from cellular or viral sources) in a physiological-like folding buffer. We typically use a simple standard solution [50 mM HEPES (pH 8.0), 200 mM potassium acetate (pH 8.0), 3 mM MgCl₂], and incubate at 37 °C for 10 – 30 min prior to modification. SHAPE works well under a wide variety of conditions, including in the presence of biological amines and carbohydrates and proteins that bind RNA. The main requirement for SHAPE is that the pH be maintained in the 7.6 – 8.3 range [38].

RNA structure is interrogated by adding a SHAPE reagent. Initial work in our laboratory used the commercially available NMIA reagent [58]; more recent work has utilized the faster-reacting 1M7 reagent, whose synthesis is described in [62]. The SHAPE reagent is dissolved in DMSO and added to the RNA solution to a final concentration of about 5 mM. The optimal reagent concentration varies and can be system-specific: too high a concentration of SHAPE reagent results in significant signal decay and reduced read lengths, while too low a concentration yields data with a poor signal. Background signals in the primer extension reaction are measured by performing a no-reagent control in which DMSO is added in place of the SHAPE reagent, in an otherwise identical reaction. Both reactions should be incubated at 37 °C for either 35 min if using NMIA or 70 sec if using 1M7. Both reagents self-quench by reacting with water in the aqueous solution.

Following an ethanol precipitation step, fluorescently-labeled primers are annealed to the (+) and (−) reagent-treated RNA and to untreated RNAs (the latter are used for sequencing). A thermostable reverse transcriptase enzyme is used for the primer extension reactions to convert the structural information into cDNA libraries. We perform the separation step in a single capillary by employing 3-4 different dyes for the (+) reagent, (−) reagent, and dideoxy sequencing ladder(s) [39, 59]. The dyes are chosen to have similar electrophoretic mobilities, which simplifies the alignment of the electropherograms during the data processing steps. The cDNA products are recovered by ethanol precipitation, resuspended in formamide, and resolved on a commercial capillary electrophoresis DNA sequencing instrument.

2.3 Data Analysis to Create Normalized SHAPE Reactivities

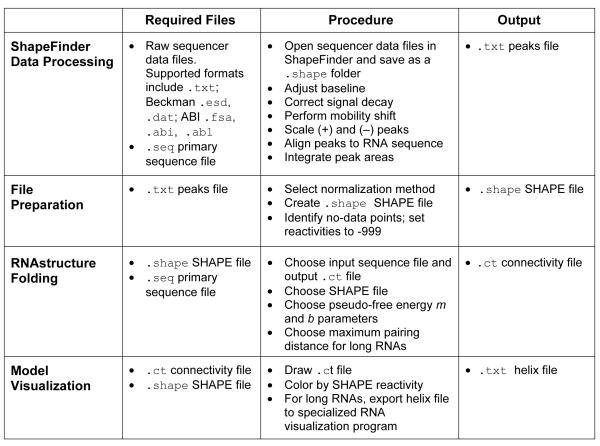
The ShapeFinder software has been described in detail [60] and is freely available for download, with tutorials [63]. Here we briefly outline the steps required to convert capillary electrophoresis electropherograms into quantitative reactivity measurements (Fig. 2).

Figure 2.

Overview of the steps involved in processing capillary electrophoresis data, obtaining normalized SHAPE reactivities, and calculating experimentally-informed RNA secondary structure models [11, 30, 39, 60].

The raw sequencer data file is opened in ShapeFinder and saved as a .shape folder. The first step is to correct baselines using the Fitted Baseline Adjust tool. Second, fluorescence intensity decays exponentially with increasing cDNA length due to incomplete processivity of the reverse transcriptase enzyme during primer extension [44, 60]. This is corrected using the Signal Decay Correction tool. Third, the Mobility Shift tool is used to align (+) reagent, (−) reagent, and dideoxy sequencing traces, since the different fluorescent dyes introduce small offsets in the raw electropherogram in their respective labeled cDNA fragments. Mobility shifts are performed manually using the sliding traces function in ShapeFinder. Fourth, the (+) and (−) reagent traces are scaled to each other to account for differences in signal intensity between the dyes. In general, the lowest (+) reagent peaks, corresponding to low or no SHAPE reactivity, should be scaled to overlap with their corresponding (−) reagent peaks. Finally, the Align and Integrate tool is used to align all peaks with the known primary sequence (supplied as a .seq text file), to make minor adjustments in peak alignments, and to integrate all peaks in the (+) and (−) reagent traces. When the calculation is complete, a text file called the peaks file is generated (Fig. 2). This file contains information about each nucleotide, including integrated (+) and (−) reagent peak areas (labeled RX and BG, respectively) and their subtracted, normalized SHAPE reactivities.

3.1 SHAPE-Constrained RNAstructure Folding: Theory

A major challenging endeavor in RNA biology is to consistently and efficiently develop correct secondary structure models for RNAs of arbitrary length and complexity. The thermodynamics-based computational methods outlined above (Section 1.1) are highly useful for rapid computation of candidate structural models. However, prediction accuracies are inconsistent for many RNAs and tend to be particularly poor for large RNAs. These limitations can be broadly attributed to simplifications inherent in the nearest-neighbor model and incomplete knowledge of RNA energetics. However, for many RNAs, it is possible to obtain robust secondary structure predictions by incorporating SHAPE reactivities into the energy function used in a nearest neighbor dynamic programming algorithm. This approach has been implemented in the RNAstructure program [64].

The RNAstructure energy function is modified by adding pseudo-free energy change terms derived from SHAPE reactivities. This approach is grounded in the observation that SHAPE reactivities correlate strongly with local nucleotide flexibility [38, 40] and, thus, also with the probability that a nucleotide is single stranded. The NMIA and 1M7 SHAPE reagents react with all four RNA nucleotides with limited base-dependent preferences [65]. It is therefore possible to create a softer, continuous, and more physically grounded restraint function than is typically used with conventional chemical mapping reagents that exhibit strong idiosyncratic and nucleotide-specific reactivities. In essence, these additional energetic terms provide a knowledge-based correction to the nearest-neighbor energy function.

We derive a pseudo-free energy change term for each base-paired residue i from its SHAPE reactivity:

$$\Delta G_{\text{SHAPE}}\left(i\right)=m\ln \left[\text{SHAPE reactivity}\right]\left(i\right)+1]+b$$ (1)

The empirical parameters m and b serve to scale the strength of the experimental contribution to the energy function. The intercept b represents the pseudo-free energy contribution of a base-paired nucleotide whose SHAPE reactivity is zero. The sign of b is negative to reflect an energetic bonus for base pairing by constrained nucleotides. In contrast, the slope m represents the strength of the energetic penalty assigned for pairing nucleotides with high SHAPE reactivities and consequently has a positive sign.

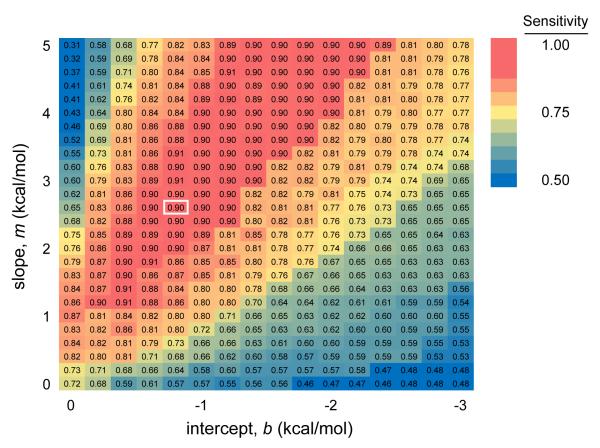
Optimal values for m and b were determined by assessing the prediction accuracy for E. coli 23S rRNA over a range of slope and intercept values [30]. This work identified m = 2.6 kcal/mol and b = −0.8 kcal/mol as optimal values for folding large ribosomal RNAs and, importantly, also established these values as being located at the center of a “sweet spot” of a broad set of m and b values that yields accurate SHAPE-directed structure predictions [30] (emphasized in red, Fig. 3). Given the large size (2,904 nts) of the E. coli 23S rRNA and the diversity of structural motifs it contains, these parameter values are also likely to work well for other RNAs. We empirically find this to be the case, although slightly different parameter values, still in the sweet spot (Fig. 3), can be chosen heuristically to refine predictions for some RNAs [41]. The logarithmic relationship between SHAPE reactivities and the derived ΔG_SHAPE term has the effect of forgiving differences among the most highly reactive nucleotides. The usefulness of this behavior reflects the observation that highly reactive nucleotides are the most sensitive to signal processing artifacts and have the highest variance. Furthermore, the logarithmic relationship between SHAPE reactivity and pseudo-free energy change loosely reflects a statistical mechanical interpretation of SHAPE reactivity, which indirectly measures the number of conformational states accessible to each nucleotide.

Figure 3.

Base pair prediction sensitivities for E. coli 23S rRNA for a range of slope (m) and intercept (b) values (Eqn. 1). Optimal values of m = 2.6 kcal/mol and b = −0.6 kcal/mol are depicted by the white box. Adapted from ref. [30].

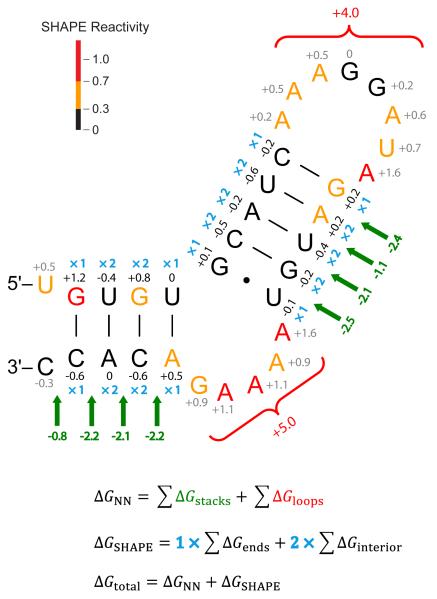
We illustrate the combined nearest-neighbor and SHAPE energy function, as implemented in RNAstructure, for a short fragment of an HIV-1 RNA sequence (Fig. 4). Nucleotides are color-coded by their SHAPE reactivities as reported in [41]. The energy function [12] includes favorable nearest-neighbor energy terms for helix stacking (in green, Fig. 4) and entropic penalties for anchoring loops (in red, Fig. 4). Stacking terms are added for all helical interactions, including terminal mismatches and dangling ends at helix termini, as well as for coaxial stacking between adjacent helices [25, 66]. Stacking terms depend on the sequence identity of all nucleotides participating in the stack (the nearest-neighbors), while loop entropy terms depend primarily on the number of nucleotides in the loop.

Figure 4.

Summary of thermodynamic and SHAPE-derived free energy change contributions for a simple HIV-1 hairpin (NL4-3 nucleotides 594 – 626) [41]. Favorable nearest-neighbor stacking and unfavorable loop thermodynamic terms are shown in green and red, respectively. The total nearest neighbor free energy change ΔG_NN is the sum over all these contributions. ΔG_SHAPE pseudo-free energy change terms are shown for base paired (black) and non-base paired (gray) nucleotides; only base paired values are included in the net free energy change. The ΔG_SHAPE term is added once for each nucleotide at the ends of helices and twice for interior nucleotides (blue symbols). The ΔG_SHAPE calculations used m = 3.0 kcal/mol and b = −0.6 kcal/mol. The total folding free energy change, ΔG_total, is the sum of nearest neighbor and SHAPE-derived contributions.

In contrast to the nearest-neighbor thermodynamics-based energy parameters, pseudo-free energy terms (ΔG_SHAPE) are calculated for each nucleotide individually (Fig. 4, black and gray numbers). Nucleotides with high SHAPE reactivities have positive pseudo-free energies and those with low SHAPE reactivities have negative pseudo-free energies (Eqn. 1). ΔG_SHAPE terms are only added to the free energy calculation for base paired nucleotides (Fig. 4, black numbers). ΔG_SHAPE terms for nucleotides at the ends of helices are counted once and those in the interior of helices are counted twice since they contribute to two stacks (Fig. 4, blue ×1 and ×2 symbols, respectively). Base paired nucleotides with high SHAPE reactivities contribute large positive pseudo-free energies (for example, see the red G in Fig. 4). Such nucleotides are more likely to be allowed at the end, as opposed to the interior, of a helix because they are added to the total free energy only once. This is consistent with the observation that nucleotides at the ends of helices are more dynamic, and experience greater fraying, than interior nucleotides. On the other hand, unpaired nucleotides with low SHAPE reactivities represent an incomplete model and could suggest non-canonical interactions that are not currently predicted by the algorithm (for example, see the tandem black G residues in the apical loop of Fig. 4). The total folding energy (ΔG_total) is simply the sum of all nearest neighbor thermodynamic terms (ΔG_NN) and pseudo-free energy (ΔG_SHAPE) contributions (Fig. 4). This sum is used to rank RNA structures and should not be interpreted as a physical energy because it includes both thermodynamic terms and SHAPE-derived pseudo-free energy change terms.

3.2 SHAPE-Constrained RNAstructure Folding: Procedure

The final output of ShapeFinder peak integration is a tab-delimited text file termed the peaks file (Fig. 2, top). Columns in the file include integrated peak areas for the (+) and (−) reagent traces, their subtracted areas, and absolute SHAPE reactivities.

3.2.1 Normalization

SHAPE reactivities are normalized to a uniform scale that is valid for diverse RNAs. Some RNAs are highly structured, with relatively few unconstrained nucleotides, while other RNAs contain large flexible loop regions. In developing a normalization procedure, we make the fundamental assumption that all RNAs will have at least a few unreactive and also a few highly reactive positions, corresponding to strongly constrained and highly dynamic nucleotides, respectively. Experience in our laboratory has found that secondary structure calculations are tolerant of variation in the absolute normalization scale, and instead depend primarily on the relative differences in SHAPE reactivities.

A normalized reactivity of 1.0 is defined as the average intensity of the top 10% most reactive peaks, excluding a few highly reactive nucleotides taken to be outliers. We use two distinct approaches to identify outlier peaks, the choice of which varies depending on the system under study. In the simple normalization scheme, the most reactive 2% of all intensities are removed from the pool. The intensities of the next 8% most reactive peaks are averaged and all reactivities are divided by this average value. This heuristic rule is based on general experience in our laboratory.

In the box-plot normalization scheme, peaks greater than 1.5 times the interquartile range (numerical distance between the 25^th and 75^th percentiles) above the 75^th percentile are removed. This definition of outliers is consistent with common practice in model-free statistics [67]. After excluding these outliers, the next 10% of intensities are averaged and all reactivities, including outliers, are divided by this value. Generally, we suggest using the box-plot method if the sequence is long enough for meaningful statistics to be calculated (typically > 300 reactivity measurements). Advanced users may opt to calculate their own normalized SHAPE reactivities if a particular experiment has a large number of very reactive peaks. The net result of normalization is to place all reactivities on a scale spanning 0 to ~1.5, where 0 indicates no reactivity (and a highly constrained nucleotide) and reactivities >0.7 typically indicate highly flexible nucleotides.

3.2.2 Maximum Pairing Distance in Large RNAs

For large RNAs, we typically disallow base-pairing between nucleotides greater than 600 positions distant from each other in the primary sequence. More than 99% of all known ribosomal RNA pairings span less than 600 nucleotides and applying this restriction increases prediction accuracy for the 16S and 23S rRNAs [30]. Applying this constraint is also attractive from the perspective of RNA folding kinetics, since RNA folding likely occurs co-transcriptionally, and nucleotides located very far from each other are unlikely to have the opportunity to base pair. This constraint thus represents a very approximate approach for accounting for RNA folding kinetics, which are otherwise ignored in a conventional thermodynamic nearest-neighbor or our SHAPE pseudo-free energy folding algorithm.

3.2.3 File Preparation

SHAPE-constrained RNA secondary structure calculations using the RNAstructure program require two input text files: (1) a sequence file with a .seq extension that contains the primary sequence, and (2) a SHAPE reactivity file with a .shape extension (Fig. 2). The sequence file format has at least one comment line, each preceded by a semicolon, followed by a one-line title, followed by the RNA sequence. The numeral 1 signals the end of the sequence. The sequence should be entered in uppercase; lowercase letters may be included and indicate nucleotides that the user specifically wishes to prohibit from base pairing (an alternative method using the .shape file is also described below). Any T’s present in the sequence are interpreted as U’s.

The user creates a .shape file as a text file containing two columns: the numerical nucleotide position and the SHAPE reactivity for that position. It is important to differentiate positions where the measured reactivity is zero from positions where no data was obtained or SHAPE reactivities could not be determined. The measurement of zero is a critical one and indicates that a position is highly structured. If the reagent and background traces were properly scaled in the ShapeFinder analysis step, there should be no, or very few, negative SHAPE reactivity values. Negative peaks are treated as having a SHAPE reactivity of zero (provided they are > −500).

SHAPE reactivities for a few nucleotides typically need to be excluded from the folding calculation. These no-data positions include nucleotides with high background in the no-reagent control and difficult-to-resolve peaks either near the 3′ primer annealing site or at the 5′ end of the trace. For such positions, one of two methods is used to signal the RNAstructure program to use only thermodynamic parameters when calculating energies involving these nucleotides. The row containing the nucleotide number and its reactivity can be deleted from the .shape file or the SHAPE reactivity can be replaced with a value ≤ −500. We typically use the latter approach and set uncertain nucleotides to -999. For a carefully performed experiment, only a small number of positions typically need to be excluded. For example, out of >9000 nucleotides in the NL4-3 HIV-1 genome, only 53 nucleotides needed to be excluded from the ΔG_SHAPE pseudo-free energy calculation. Finally, known single stranded regions or those that interact with another RNA or protein can be prohibited from forming base pairs by assigning these nucleotides a high SHAPE reactivity value (by convention, we set these to 100). This was important, for example, in folding calculations for an HIV-1 genome at positions that form intermolecular base pairs with the tRNA primer [41].

3.2.4 RNAstructure

After preparing the sequence and SHAPE text files, the user is ready to initiate folding in RNAstructure via RNA/Fold RNA Single Strand, then selecting the input sequence and output connectivity files (.ct file, Fig. 2). The sequence can also be input by hand via File/New Sequence. For large RNAs, we usually restrict base pair distances to less than 600 nucleotides via Force/Maximum Pairing Distance. SHAPE data are then read via Force/Read SHAPE Reactivity – Pseudo-Energy Constraint at which point the slope (m) and intercept (b) (Eqn. 1) are chosen. Optimal values of m = 2.6 kcal/mol and b = − 0.8 kcal/mol were obtained by optimizing structural predictions for 23S rRNA, but there is a range of values that yield high prediction accuracies (Fig. 3) [30]. We empirically find that different weights within this range may be optimal for other RNAs. For example, in our current HIV-1 work, we use values of m = 3.0 kcal/mol and b = −0.6 kcal/mol [41]. The user accepts the SHAPE file and initiates the folding calculation by selecting START.

3.2.5 Model Visualization

The completed calculation generates a .ct file and the user is prompted with the option of drawing the resulting secondary structures. Viewing perspectives are manipulated under the Draw tab in RNAstructure. The structure can be colored by SHAPE reactivity via Draw/Add SHAPE annotation and choosing the appropriate .shape file. Nucleotides are drawn using the following convention [30]: SHAPE reactivities < 0.3 are black; those ≥ 0.7, red; those in between, orange; and those without SHAPE data, gray (Fig. 4).

An RNA secondary structure model is consistent with the input SHAPE reactivities if double stranded regions are generally black and single stranded nucleotides red or orange. While the RNAstructure viewer is useful for analyzing predicted structures, for presentation quality images and large RNAs, we recommend exporting the structures as helix text files (Draw/Export Structure to Text File) that can be read by viewing software such as XRNA [68]. The .ct file displays the total folding energy corresponding to the sum of both thermodynamic and SHAPE-derived pseudo-free energy change contributions (see Fig. 4). The folding energy that corresponds solely to the sum of thermodynamic terms can be obtained by running RNA/Efn2 RNA on the .ct file.

4. Example: A SHAPE-Supported Model for the HIV-1 Gag-Pol Frameshift Element

We conclude this review with an example from HIV-1 biology describing how SHAPE-constrained RNAstructure calculations can be used to propose new structural models for RNA domains. The human immunodeficiency virus maximizes coding efficiency through the use of overlapping reading frames in its RNA genome. The gene coding for Pol, the polyprotein precursor for viral enzymes, does not have its own start codon but, instead, is encoded in an open reading frame that is offset by -1 nucleotide relative to the upstream Gag reading frame. In order to translate Pol, the ribosome initially translates Gag before pausing, backing up 1 nucleotide, and proceeding to translate the pol reading frame [69]. This process is called frameshifting and occurs at a conserved heptanucleotide UUUUUUA “slippery” sequence with a frequency of approximately 5-10% [70, 71]. The precise level of frameshifting is crucial for viral replication and the ratio of Gag to Gag-Pol polyprotein products appears to be tightly regulated [72]. The HIV-1 frameshift element is thus an intriguing target for antiretroviral drug development [71, 73].

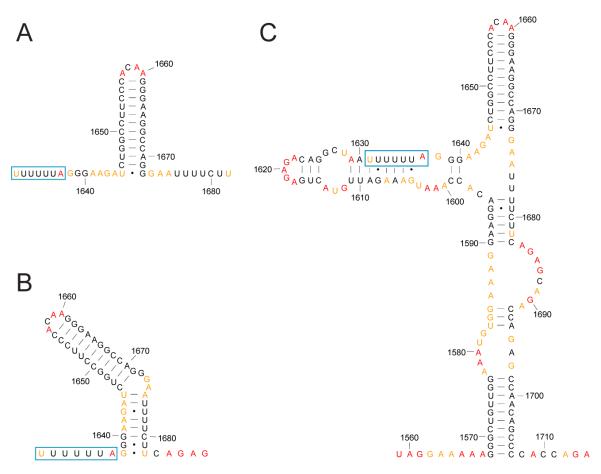
The Gag-Pol frameshift element has traditionally been drawn as consisting of a single stranded slippery sequence followed by a downstream stimulatory element consisting of a 12 base pair hairpin structure (Fig. 5A). This stem-loop RNA structural element functions to enhance ribosomal pausing and to increase the frequency of frameshifting [74]. However, comparisons with ribosomal frameshift structures from other retroviruses and experimental evidence that this classical stem-loop is necessary, but not sufficient, for frameshifting [75, 76] have motivated alternative proposals for this element. These alternative structures include pseudoknots [77-79] and a two-stem model (Fig. 5B) [80]. The two-stem model was confirmed by NMR studies performed on 41 and 45 nucleotide transcripts containing precisely this region [81, 82].

Figure 5.

RNA secondary structure models for the HIV-1 M-group Gag-Pol frameshift element. All models are colored by their SHAPE reactivities as reported in [41] using the scale shown in Figure 4. The “slippery sequence” where frameshifting occurs is enclosed in a blue box. The numbering is for the NL4-3 reference sequence. (A) Classical model [69]. (B) Two-stem model [80]. (C) SHAPE-supported model [41].

However, SHAPE probing of the full-length HIV-1 RNA genome, as extracted from authentic viruses, suggests yet another, more complex, structure (Fig. 5C) [41]. Most strikingly, nucleotides in the slippery sequence (blue boxes, Fig. 5) have mostly low SHAPE reactivities. These experimental measurements indicate that the slippery sequence is base paired (or otherwise constrained) rather than being single stranded in the intact genome as isolated from viruses. Furthermore, when SHAPE reactivities are used to direct RNAstructure folding calculations of the entire intact genome, analysis of the frameshift region in its global context suggests that this functional element is one part of a much larger, 140-nucleotide long, structural unit (Fig. 5C). Further work will clearly be needed to discriminate among these models and to determine whether the frameshift element might adopt multiple conformations during HIV-1 replication. However, this example illustrates the ability of SHAPE-constrained folding to identify elements of current models that may be incomplete and to facilitate development of new RNA structure models in the context of their global, native-like, sequence and structural environments.

5. Conclusions

The SHAPE-constrained RNA folding approach outlined here provides a straightforward way of proposing, validating, and refining accurate secondary structure models for nearly any RNA. Current limitations in the SHAPE approach remain active research focuses, including the requirement for pmol-scale amounts of RNA, which can be difficult to obtain in some cases, and the inability to directly predict pseudoknots and other tertiary interactions. SHAPE-constrained RNA folding is particularly valuable for the large universe of functionally important RNAs for which there is little evolutionary data and for which high-resolution structure determination is unrealizable. In addition, the ability to probe RNA structures in cellular and viral environments or in native-like extracted forms can provide biological insights that are not obtainable using simplified in vitro models. Continued development of SHAPE reagents and of algorithms for using experimental information to constrain RNA structure prediction will expand the classes of RNA motifs and structure-function relationships that can be understood at a molecular level.