Positive autoregulation shapes response timing and intensity in two-component signal transduction systems

Abstract

Positive feedback loops are regulatory elements that can modulate expression output, kinetics and noise in genetic circuits. Transcriptional regulators participating in such loops are often expressed from two promoters – one constitutive and one autoregulated. Here we investigate the interplay of promoter strengths and the intensity of the stimulus activating the transcriptional regulator in defining the output of a positively autoregulated genetic circuit. Using a mathematical model of two-component regulatory systems, which are present in all domains of life, we establish that positive feedback strongly affects the steady-state output levels at both low and high stimulus if the regulator’s constitutive promoter is weak. By contrast, the effect of positive feedback is negligible when the constitutive promoter is sufficiently strong, unless the stimulus intensity is very high. Furthermore, we determine that positive feedback can affect both transient and steady-state output levels even in the simplest genetic regulatory systems. We tested our modeling predictions by abolishing the positive feedback loop in the two-component regulatory system PhoP/PhoQ of Salmonella enterica, which resulted in diminished induction of PhoP-activated genes.

Introduction

Feedback loops are common elements of cellular regulatory circuits^1;2;3;4;5. In the simplest example of feedback, a transcription factor binds to the promoter of its own gene, thereby stimulating^4;6;7 or repressing^8;9 its own expression. Feedback can influence an autoregulated system’s output by affecting its quantitative properties, such as response timing^10;11, response levels^7;12, and genetic noise¹³. Feedback regulation is critical for enzymatic control in archaea¹⁴, development in eukaryotic organisms⁴ and virulence in bacterial pathogens^7;15. While it is generally accepted that positive feedback can play a defining role in a genetic circuit, the factors governing the magnitude of its effect have remained largely unexplored. Here, we investigate how the intensity of an inducing signal and the expression levels shape the output of positively autoregulated two-component systems (TCSs), a prevalent form of signal transduction in bacteria, also found in fungi, plants and archaea^4;16;17.

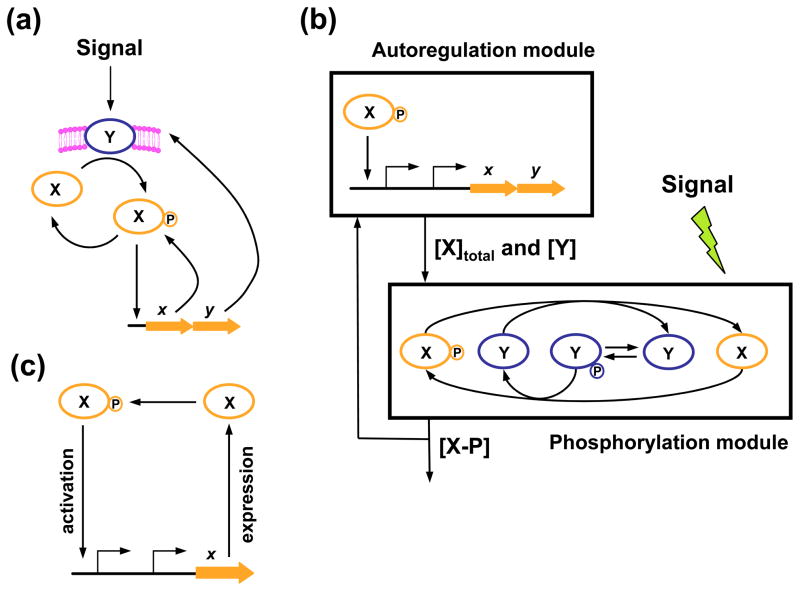
The prototypical TCS consists of two proteins, a sensor and a transcriptional regulator^17;18;19 (Fig. 1a). The sensor responds to the presence of an activating signal by autophosphorylating from ATP and then transferring the phosphoryl group to the regulator, thereby increasing the regulator’s ability to bind to DNA and modulate expression of its target genes. In the absence of an activating signal, sensors often act as phosphatases towards the phosphorylated form of their cognate regulators. Thus, the output of a TCS (i.e., the level of the phosphorylated regulator) is determined by the balance of the phosphorylation and dephosphorylation reactions mediated by the sensor, which, in turn, can be modulated by other proteins and/or peptides^19;20;21;22. The sensor and regulator for a particular TCS are typically encoded in the same operon, which is often transcribed from two promoters: one constitutive and one autoregulated^4;8 (Fig. 1a). The constitutive promoter is responsible for the production of basal levels of the sensor and regulator proteins, which are necessary to detect and to respond to a change in conditions. The positively autoregulated promoter is critical as its absence can impact both how a system reaches a particular steady state⁷ and the steady-state output that is achieved⁶.

Fig. 1.

Genetic regulatory architectures with positive feedback. (a) Prototypic two-component signal transduction system. X – regulator protein, Y – sensor protein; x and y denote the corresponding genes, which are part of the same operon. Phosphorylated regulator binds with the genes’ autoregulated promoter and activates transcription. (b) The modular model of two-component signal transduction (redrawn from Ref. 6 with modifications). The phosphorylation module determines the concentration of X-P (phosphorylated regulator) as a function of the total sensor and regulator concentrations and the intensity of the activating stimulus. The autoregulation module defines the total sensor and regulator concentrations given the concentration of phosphorylated regulator. (c) A dynamic model of positive autoregulation introduced in Ref. 4. The regulator X (in phosphorylated form) can directly activate expression of its own gene.

Investigations carried out with the well-characterized PhoP/PhoQ TCS (reviewed in Ref. 23;24) have revealed that, on the one hand, positive feedback is necessary for the surge in phosphorylated PhoP protein and the ensuing transcriptional surge of PhoP-activated mRNAs taking place when Salmonella enterica experiences inducing conditions for the PhoQ protein and before it reaches a new steady-state⁷. On the other hand, abrogation of positive feedback in the PhoP/PhoQ system of Escherichia coli impacted its steady-state output level in organisms experiencing high stimulus, but, surprisingly, not in those facing low or intermediate stimulus levels⁶.

We now present a combination of mathematical modeling and experimental results demonstrating that for a regulatory protein that is expressed from both constitutive and autoregulated promoters, positive feedback can have a significant effect on the system’s steady-state behavior in cells experiencing low as well as high stimulus, and that the effect of positive feedback depends on the strength of the constitutive promoter. Our modeling predictions were validated by showing that changes in the expression levels of PhoP-activated genes resulting from ablation of the positive feedback loop regulating the expression of the PhoP/PhoQ TCS in S. enterica. Further validation was provided by comparisons of PhoP-activated gene expression in organisms that differ in the strength of the constitutive promoter driving transcription of the phoP and phoQ genes. We establish that, even in the simplest autoregulated systems, positive feedback can affect the steady-state output as well as how a system reaches a particular steady state. Our findings may help the design of synthetic genetic circuits with positive feedback control.

Results

Steady-state modular model of a two-component system

We explored the quantitative effects of positive feedback using a modular model of a TCS introduced previously by the Goulian laboratory^6;25 (Fig. 1b). The model, which provides a steady-state description of a TCS’s quantitative behavior, consists of two modules – the phosphorylation module and the autoregulation module (Fig. 1b). The phosphorylation module reflects the processes of sensor autophosphorylation, phosphotransfer from phosphorylated sensor to unphosphorylated regulator, and dephosphorylation of the phosphorylated regulator by the sensor protein. The input of this module includes (i) the intensity of the signal sensed by the system, and (ii) the total concentrations of the sensor and regulator proteins. The output of the system is the concentration of phosphorylated regulator. The autoregulation module reflects the dependency of the concentration of phosphorylated regulator (i.e., the module’s input) on the total concentrations of the sensor and regulator proteins (i.e., the module’s output). This module accounts for: (i) expression of the sensor- and regulator-encoding genes (which belong to the same operon) from both a constitutive promoter and a positively autoregulated promoter, and (ii) changes in the amounts of the sensor and regulator proteins due to degradation and dilution.

The state of the system is determined by two variables: the total concentration of regulator (phosphorylated and unphosphorylated forms) and the concentration of the phosphorylated regulator. (In the model, the total concentration of the sensor is proportional (with a small proportionality coefficient) to that of the regulator⁶.) This state, which corresponds to the steady state of the biochemical system, is unique and can be found by solving a system of two algebraic equations⁶:

$${[\text{R}]}_{\mathit{total}}=\tau B+\frac{\tau A[\text{R}-\text{P}]}{D+[\text{R}-\text{P}]}$$ (1)

and

$$[\text{R}-\text{P}]=\frac{1}{2}(C_t+C_p+{[\text{R}]}_{\mathit{total}})-\frac{1}{2}\sqrt{{(C_t+C_p+{[\text{R}]}_{\mathit{total}})}^2-4C_p{[\text{R}]}_{\mathit{total}}},$$ (2)

where [R] and [R - P] are the total concentration of the regulator and the concentration of phosphorylated regulator in the system, respectively; τ=1/λ, where λ is the degradation/dilution rate for the regulator; A and B are the regulator synthesis rates for the autoregulated and constitutive promoters, respectively. We use the term “promoter strength” to designate these values (and also for the proportional values τA and τB). D denotes the strength of the interaction between the phosphorylated regulator protein and the autoregulated promoter. The constants C_t and C_p are proportional to the Michaelis constants for the sensor-catalyzed phosphotransfer and phosphatase reactions, respectively^6;25. The value of C_p reflects stimulus intensity: stronger stimuli correspond to higher values of C_p.

Positive feedback impacts output levels in two-component systems with weak constitutive promoters regardless of stimulus intensity

Because transcription output in a TCS is determined by the amount of phosphorylated regulator⁷, we hypothesized that the contribution of positive feedback to TCS output might depend on the relative strengths of the constitutive and autoregulated promoters. Thus, we explored the dependency of a system’s output on the strength of its constitutive promoter for both low and high stimulus conditions. Our mathematical analysis of Eqs. (1)–(2) allowed us to characterize the model’s output level for strong constitutive promoters: in the limit of large total concentration of the regulator protein ([R]_total), the output of the phosphorylation module reaches the value [R - P] = C_p (Supporting Information, Eq. (S3)). Furthermore, the total concentration of the regulator is an increasing function of the constitutive promoter strength, i.e. B (see Supporting Information for a mathematical argument). Therefore, when the constitutive promoter is sufficiently strong, the system achieves steady state at a high total regulator concentration, and the output of the system is [R - P] ≈ C_p. Because the stimulus intensity (and, therefore, C_p) does not depend on the strength of the autoregulated promoter, the system’s output is approximately equal to C_p for strong constitutive promoters in systems both with and without feedback. This analysis indicates that for systems with sufficiently strong constitutive promoters the output is independent of positive feedback regardless of the input signal intensity.

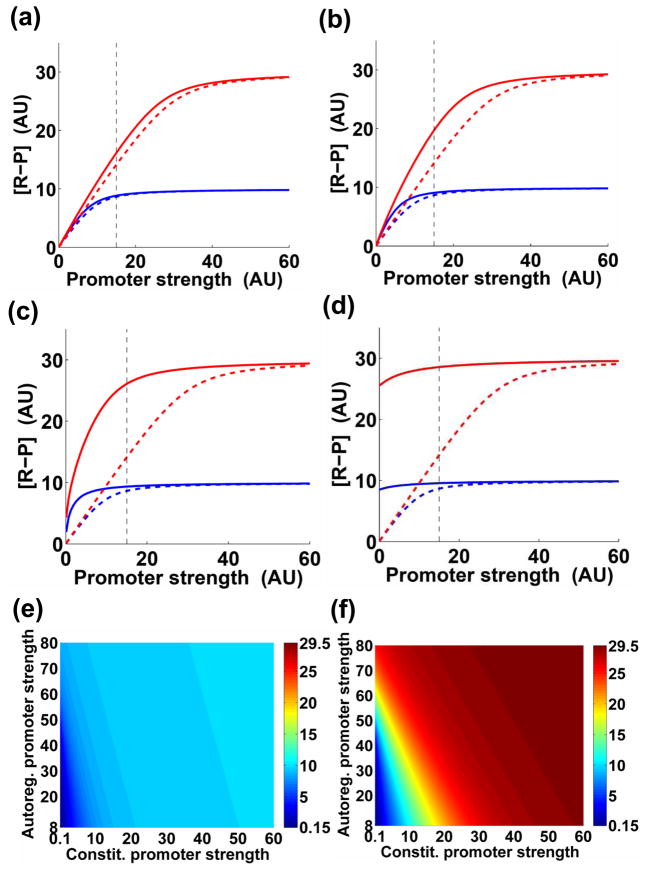
To explore the possibility that the impact of positive feedback depends on the strength of the constitutive promoter, we solved Eqs. (1)–(2) numerically for different autoregulated and constitutive promoter strengths (i.e., different values of τA and τB, respectively). For the remaining parameters, we used nominal values that were identical to those previously used in Ref. 6 (see also Supporting Information). We performed computations for two levels of activating signal – low stimulus (C_p =10) and high stimulus (C_p = 30), as previously considered⁶.

We established that a difference in output levels between systems with (A > 0) and without (A = 0) positive feedback regulation depends on the strength of the constitutive promoter (Fig. 2). As predicted (Supporting Information, Eq. (S3)), the phosphorylated regulator level for strong constitutive promoters converges to the limiting value that equals C_p (Fig. 2). However, in the case of high stimulus this convergence is slower: for a given value of autoregulated promoter strength, the discrepancy between the cases with and without positive feedback is more pronounced for high stimulus than for low stimulus. This result explains the previous observation made for a specific pair of promoter strengths (i.e., τA = 45 and τB = 15), which has led to the proposal that positive feedback impacts the output levels in the case of high, but not low, stimulus⁶ (Fig. 2c).

Fig. 2.

Positive feedback impacts the steady-state output levels of the modular model of a two-component system (Fig. 1b; Eqs. (1)–(2)). (a)–(d): x-axis, constitutive promoter strength (τB; Eq. (1)); y-axis, concentration of phosphorylated regulator; AU – arbitrary units. Blue and red lines correspond to low and high stimulus, respectively. Solid lines – positive feedback present; dashed lines – positive feedback absent. Dashed black line marks the value τB=15, chosen as the nominal value in Ref. 6. The strength of the autoregulated promoter is reflected by the value of τA. (a) τA=8. (b) τA = 20. (c) τA = 45 (chosen as the nominal value in Ref. 6). (d) τA = 80. (e)–(f): dependency of the system output level on the strength of the constitutive and autoregulated promoters. Color coding designates [R - P]. (e) Low stimulus; (f) high stimulus.

We identified a significant difference in the output levels between the cases with and without positive feedback for both low and high stimuli when the autoregulated promoter is sufficiently strong, and the constitutive promoter strength is below the nominal value (i.e., τB < 15) (Fig. 2c, d). This difference becomes more pronounced as the strength of the autoregulated promoter increases. Thus, even for the nominal autoregulated promoter strength (i.e., τA = 45) under the condition of low stimulus, abrogation of positive feedback can lead to a >3-fold decrease in the output level, which happens when τB < 3 (Fig. 2c). Cumulatively, our analysis demonstrates that the relative contribution of positive feedback depends on the particular strengths of both the constitutive promoter and the autoregulated promoter driving transcription of a regulatory protein/system. When the constitutive promoter is weak, positive feedback exerts a significant influence on the system’s output level. By contrast, when the constitutive promoter is sufficiently strong, the dependency of the output levels on feedback is negligible for both low and high stimulus (Fig. 2e,f).

Positive feedback affects steady-state output levels in systems with strong autoregulated promoters

Because the modular model discussed above (Eqs. (1)–(2)) cannot be immediately extended to describe the time-dependent behavior of positively autoregulated systems, we explored the effect of positive feedback in a recently introduced dynamic model of transcriptional control that accounts for phosphorylation and autoregulation⁴. The dynamic model describes both the transient and steady-state dynamics of a system consisting of a regulatory protein present in its unphosphorylated and phosphorylated forms, as well as the gene encoding this protein (Fig. 1c). The concentration of the phosphorylated regulator protein is the model’s output. The model reflects the situation when a phosphorylated regulator can directly activate the promoter of its own gene. In addition to the autoregulated promoter, a constitutive promoter transcribes the gene encoding the regulator. In the model, the phosphorylation and dephosphorylation rates can be regarded as the inputs because the system is activated or deactivated as a result of changes in phosphorylation and/or dephosphorylation rates of the regulator.

The dynamic transcription regulation model is defined by the following differential equations⁴:

$$\frac{d[\text{R}-\text{P}]}{dt}=k_a[\text{R}]-(k_{-a}+k_d)[\text{R}-\text{P}]$$ (3)

and

$$\frac{d[\text{R}]}{dt}=k_1+k_2\frac{K{[\text{R}-\text{P}]}^H}{1+K{[\text{R}-\text{P}]}^H}+k_{-a}[\text{R}-\text{P}]-(k_a+k_d)[\text{R}].$$ (4)

In Eqs. (3)–(4), [R - P] and [R] are the concentrations of the phosphorylated and unphosphorylated forms of the regulatory protein, respectively. k_a and k_−a are the phosphorylation and dephosphorylation rates, respectively; k_d is the degradation/dilution rate for the regulator. K is the equilibrium constant for the interaction of the phosphorylated regulator with its own promoter, and H is the Hill coefficient reflecting cooperativity in this interaction. k₁ and k₂ are the regulator synthesis rates reflecting the activity (or strength) of its constitutive and autoregulated promoters, respectively. (The case of no positive feedback corresponds to k₂ = 0.) Eqs. (3)–(4) with appropriate initial conditions describe temporal changes in the concentrations of the phosphorylated and unphosphorylated regulator. The steady state of the system is the solution of Eqs. (3)–(4) in the limit of infinite time.

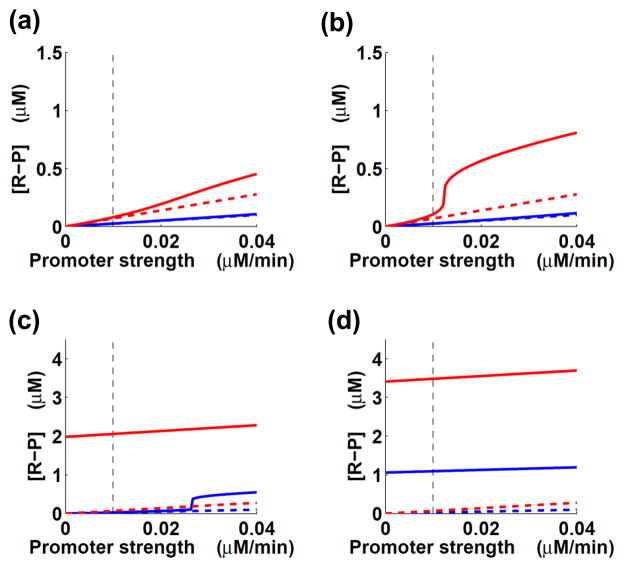
We determined the steady-state output levels for Eqs. (3)–(4) for different values of the regulator synthesis rates for the constitutive and autoregulated promoters. Computations were performed for two levels of activating signal: low stimulus (k_a = 5) and high stimulus (k_a = 25) as considered previously⁴. All other parameter values had nominal values chosen as described⁴ (see also Supporting Information). Then, we considered different scenarios based on the strength of the two promoters and the intensity of the stimulus.

When the autoregulated promoter is weak, the impact of positive feedback is negligible in the case of low stimulus, but noticeable in the case of high stimulus (Fig. 3a, b). This result resembles the behavior of the modular model of a TCS (Fig. 2b; Eqs. (1)–(2)). When the autoregulated promoter is strong, however, the impact of positive feedback is significant for both low and high stimulus (Fig. 3b–d). Taken together, our results indicate that in the simple model of transcription regulation (Eqs. (3)–(4)) positive feedback affects the model output level for sufficiently strong autoregulated promoters.

Fig. 3.

Positive feedback impacts the steady-state output levels in a positively autoregulated system (Fig. 1c; Eqs. (3)–(4)). x-axis: constitutive promoter strength (k₁; Eq. (4)); y-axis: concentration of phosphorylated regulatory protein. Blue and red lines correspond to low and high stimulus, respectively. Solid lines – positive feedback present; dashed lines – positive feedback absent. Dashed black line marks the value k₁ = 0.01 μM/min, chosen as the nominal value in Ref. 4. The strength of the autoregulated promoter is reflected by the value of k₂. (a) k₂ = 0.05μM/min. (b) k₂ = 0.1μM/min. (c) k₂ = 0.3μM/min (chosen as the nominal value in Ref. 4). (d) k₂ = 0.5μM/min.

Our findings demonstrating the role of positive feedback in the dynamic model of transcription regulation (Eqs. (3)–(4)) are consistent with our results for the model representing the steady state of a two-component system (Eqs. (1)–(2)). Yet, the shapes of the steady-state curves for the former model (Fig. 3) are qualitatively different from the corresponding curves for the latter model (Fig. 2), and this is due to differences in the mathematical models, which reflect the specific properties of these genetic regulatory systems. In the two-component system model (Eqs. (1)–(2)), the sensor protein displays both kinase and phosphatase activities²⁵. Because it is assumed that the gene specifying the sensor is co-transcribed with the gene specifying the regulator⁶, an increase in the constitutive promoter strength leads to an increase in both the kinase and phosphatase activities. Thus, the intrinsic balance between the phosphorylation and dephosphorylation reactions determines the saturation behaviour of the response, with response curves reaching a plateau for high constitutive promoter strength values (Fig. 2). By contrast, in the dynamic model of transcription regulation (Eqs. (3)–(4)), the phosphorylation and dephosphorylation intensities are independent of each other and of the regulator synthesis rate. Therefore, for fixed phosphorylation and dephosphorylation rates, an increase in the strength of the constitutive promoter results in a higher phosphorylated regulator concentration, which can increase further without reaching a plateau (Fig. 3).

The sigmoidal curves in Fig. 3b–c result from the Hill coefficient H being equal to 2 (Eq. 4), reflecting the frequently made assumption that the regulator binds to its promoters as a dimer⁴. Indeed, if we generate the steady-state curves for Eqs. (3)–(4) with H = 1, sigmoidality disappears (data not shown). The two-component system model (Eqs. (1)–(2)) has been developed under the simplifying assumption of no regulator binding cooperativity⁶, which corresponds to H = 1. As a result, all the signal–response curves for the model are hyperbolic (Fig. 3).

Abrogation of positive feedback lowers expression output of the PhoP/PhoQ system

To assess the predictions of our models on the role that positive feedback plays in a TCS, we chose to examine experimentally the positively autoregulated PhoP/PhoQ system from S. enterica because certain aspects of positive feedback in the PhoP/PhoQ system have been explored both in S. enterica and in the closely-related species E. coli^6;7;26.

We analyzed the behavior of three isogenic S. enterica strains: one harboring the wild-type autoregulated promoter as well as the constitutive promoter driving transcription of the phoPphoQ operon, one lacking the PhoP box necessary for positive feedback of the PhoP/PhoQ system but retaining the constitutive promoter, and one where the PhoP box mediating positive feedback in the wild-type promoter was replaced by a −35 consensus sequence for σ 70 RNA polymerase so that phoPphoQ transcription is driven both by a strong constitutive promoter and the natural constitutive promoter.

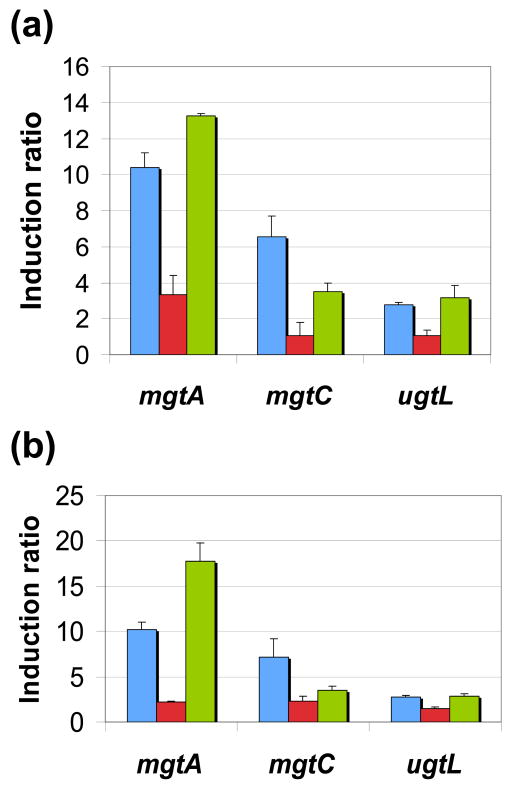
We harvested mRNA from the three isogenic strains described above following bacterial growth in the presence of 10 mM Mg²⁺, which is a non-inducing condition, and then incubated in either of two inducing Mg²⁺ concentrations (50 and 200 μM) for 90 min (see Methods). The mRNA level for three PhoP-activated genes were normalized by that corresponding to the PhoP-independent rrs gene, and the induction ratios were calculated as the rrs-normalized mRNA levels produced by the cells experiencing inducing conditions divided by those produced 5 min prior to shifting the bacteria to inducing conditions (see Methods). The mRNA induction ratios were 2–10 fold in the strain with the wild-type (positively autoregulated) phoPQ promoter (Fig. 4, blue bars), which are 3–5-fold higher than those displayed by the strain harboring the constitutive phoPQ promoter (Fig. 4, red bars). The differences in mRNA induction ratios were observed even when bacteria were grown in 200 μM Mg²⁺, which constitute mild inducing conditions for the PhoP/PhoQ system²⁷.

Fig. 4.

The impact of positive feedback in the induction ratios of PhoP-activated genes in S. enterica depends on the strength of the constitutive promoter transcribing the phoPphoQ operon. Induction ratios corresponding to the mRNA levels produced by a wild-type strain (EG13918; blue bars), a strain deleted for the PhoP box governing positive feedback of the phoPphoQ operon (EG14338; red bars), and a strain with the PhoP box in the phoPphoQ promoter substituted with the −35 hexamer consensus sequence for σ 70 RNA polymerase (EG14943; green bars). Bacteria were grown as described in Results, and RNA was isolated as described in Methods. Error bars designate standard deviation. Gene expression was measured following bacterial growth in 200 μM Mg²⁺ (a) or 50 μM Mg²⁺ (b).

The higher mRNA induction ratio displayed by the strain with the wild-type promoter relative to that with the constitutive promoter can be attributed to the fact that positive autoregulation generates higher amounts of PhoP protein in the former than in the latter strain. This would result in higher levels of phosphorylated PhoP and transcription of PhoP-activated genes. Therefore, if the PhoP protein were made constitutively at levels equivalent to those achieved by the strain with the wild-type (i.e., autoregulated) promoter, the resulting mRNA induction ratios should be similar. This prediction was verified as the strain with the phoPQ promoter harboring the −35 consensus sequence, which makes similar amounts of PhoP protein as the one with the wild-type promoter at steady-state⁷, exhibited comparable mRNA induction ratios (Fig. 4, green bars). These results indicate that the strength of the constitutive promoter driving transcription of sensor and regulator genes for a TCS determines the induction ratios for the regulated mRNAs when a TCS is not autoregulated.

Positive feedback defines the temporal behavior of gene regulation systems

Most biochemical analyses consider systems that have reached steady state. However, how a system reaches steady state can critical functions such as the ability of a bacterial pathogen to cause disease⁷. Thus, we explored the role that positive feedback plays on a regulatory system before it reaches its steady state by numerically solving Eqs. (3)–(4) for the situations when the feedback in the system is present or absent.

We established that there are considerable differences between the “feedback” and “no-feedback” trajectories in cells experiencing inducing conditions: at 20 min post-activation, the difference was 5-fold, and at 30 min post-activation, the output levels differed by an order of magnitude (Fig. 5). This took place long before the system with positive feedback reached its steady state. By contrast, the output level was low and almost independent of positive feedback under non-inducing conditions (Fig. 5), which agrees with the model when the system is at steady state (Fig. 3a). Our results suggest that the influence of positive feedback can be significant on timescales much shorter than the timescale for convergence to steady state. Therefore, even if a positively autoregulated system has not yet reached its steady state, its output level can be affected by positive feedback.

Fig. 5.

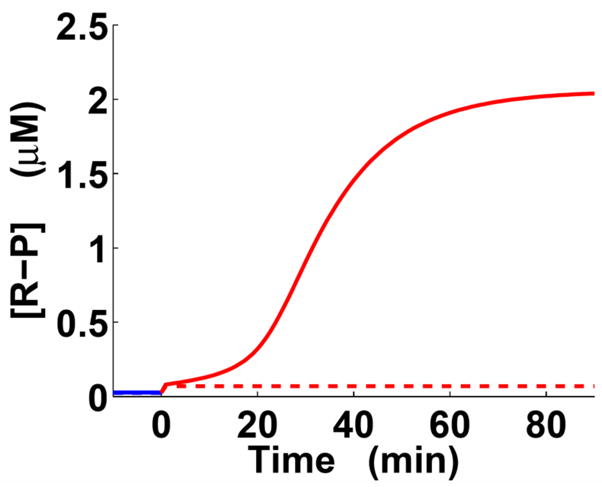
Positive feedback impacts expression output before a system reaches steady state (Fig. 1c; Eqs. (3)–(4)). Blue and red lines correspond to low and high stimulus, respectively. Solid lines – positive feedback present; dashed lines – positive feedback absent. The state of the system before and at time 0 is the steady state determined for the nominal parameter set. At time 0, the system was activated by an instantaneous 5-fold increase in the regulator phosphorylation rate (k_a).

Discussion

Positive feedback determines the behavior of signal transduction circuits⁴. Besides being widely spread in nature, positive feedback loops have often been used as components of synthetic genetic circuits with specific (e.g., oscillatory) dynamic properties^28;29;30;31. We have now carried out a comprehensive analysis of the dependency of a TCS output (i.e., the concentration of the phosphorylated regulator) on positive feedback by examining three independent variables: the strength of the constitutive promoter, the strength of the positively autoregulated promoter, and the intensity of the stimulus activating the TCS (Figs. 2–5). Our results suggest that positive feedback is a critical factor determining the output levels of genetic circuits. This conclusion is supported by the following evidence: First, the output level of a TCS is strongly dependent on positive feedback for both high and low stimulus conditions when transcription of the TCS genes is driven by a weak (as opposed to strong) constitutive promoter (Fig. 2). Second, the output level of the regulatory protein in a regulatory circuit significantly depends on the positive feedback if the autoregulated promoter controlling transcription of the corresponding gene is sufficiently strong (Fig. 3). Third, abrogation of the autoregulated promoter leads to lower levels of activated (i.e., phosphorylated) regulatory protein in a dynamic transcription regulation model (Fig. 5), thereby lowering expression output. And fourth, the mRNA levels for three genes activated by the regulatory protein PhoP from the PhoP/PhoQ two-component system decreased upon elimination of the autoregulated phoPphoQ promoter (Fig. 4).

The presence of two promoters – one constitutive and one autoregulated – appears to be widespread across genetic circuits with positive feedback⁴. The constitutive promoter is required to activate such circuits because, when the activating signal for a regulatory protein is absent, the regulatory protein is inactive and there would be no transcription from the autoregulated promoter. Thus, expression from the constitutive promoter guarantees the production of sufficient amounts of the regulatory components so a cell can respond to an activating signal when it appears.

Our analysis of the mathematical model of signal transduction by TCSs (Eqs. (1)–(2)) demonstrated that when the constitutive promoter driving transcription of TCS genes is sufficiently strong, the impact of positive feedback can be negligible regardless of signal intensity (Supporting Information, Eq. (S3)). For constitutive promoters of high or intermediate strengths, the impact of positive feedback is more significant in the case of high stimulus than in the case of mild stimulus (Fig. 2). By contrast, when the constitutive promoter is weak, positive feedback can have a strong effect on the output levels at both low and high stimulus intensities (Fig. 2b–f). These results indicate that, depending on the strength of the promoters driving transcription of the genes coding for a TCS, the effect of positive feedback may or may not be affected by the intensity of the stimulus.

The PhoP/PhoQ TCS has been shown to be autoregulated in E. coli^32;33, S. enterica^32;33 and Yersinia pestis^34;35, and genomic analysis suggest that this property is conserved in other examined enteric species³⁵. Remarkably, the ability of PhoP/PhoQ to positively control its own expression is conserved despite differences in the arrangement of the constitutive and autoregulated promoters, and/or the presence of additional open reading frames in the operon transcribing the phoP and phoQ genes^32;33;35. This indicates that positive autoregulation of the PhoP/PhoQ system is critical for its proper functioning in all these species. We have now established that deletion of the PhoP box in the S. enterica phoPQ promoter leads to a significant decrease in the mRNA induction ratios of PhoP-activated genes, even at mild stimulating conditions (i.e., 200 μM Mg²⁺) (Fig. 4). These results agree with our theoretical predictions that positive feedback can impact a system’s output levels over a broad range of signal intensities (Figs. 2–3).

In contrast to the results discussed above, the Goulian group observed differences in the expression of PhoP-activated genes between isogenic E. coli strains, one with the wild-type promoter and one lacking PhoP-mediated positive feedback, only under very high stimulus conditions⁶. We considered three possibilities to explain the distinct behaviors exhibited by E. coli and S. enterica upon elimination of PhoP autoregulation: (i) an outcome of species-specific properties; (ii) a reflection of the specific ways used to measure gene expression (direct mRNA measurement in S. enterica versus fluorescence from a reporter gene in E. coli); and (iii) a consequence of the use of an engineered E. coli strain expressing high levels of the PhoP protein constitutively⁶. Indeed, the latter possibility is at variance with the production of PhoP at undetectable levels in wild-type S. enterica experiencing non-inducing conditions when phoPphoQ transcription originates only from the constitutive promoter⁷. We favor this possibility because when we engineered a strain with a stronger constitutive promoter to drive transcription of the phoPQ genes in S. enterica, the induction mRNA ratios were higher than those present in the strain with the constitutive promoter and similar to those displayed by the strain with the wild-type autoregulated promoter (Fig. 4) as reported by the Goulian group ⁶. Moreover, our modeling indicates that, in the special case of a strong constitutive promoter driving transcription of a regulatory protein, lack of sensitivity to positive feedback is to be expected (Fig. 2). In sum, the functional advantages of positive autoregulation appear to be easier to realize in systems where the constitutive promoter is noticeably weaker than the autoregulated one, which appears to be the normal situation. This is because a strong constitutive promoter would promote high basal levels of regulator, which in the case of TCSs can lead to regulator dimerization and transcription of its target genes even in the absence of inducing signals and the regulator’s cognate sensor³⁶.

The impact of positive feedback on a circuit’s output levels determines the physiological role of this type of regulation. In the case of the PhoP/PhoQ system of S. enterica, the system’s output level (i.e., the level of PhoP-P) defines its ability to control a multitude of PhoP-regulated promoters. Because PhoP-P exhibits differential affinity for the various PhoP-activated promoters (Zwir et al., in preparation), the amount of PhoP-P generated in an organism that lacks positive feedback will be sufficient to bind to and promote transcription from high affinity promoters, such as that corresponding to the mgtA gene, but not to those that are bound weakly by the PhoP-P protein, such as those corresponding to the mgtC and ugtL genes. Because mgtC is required for S. enterica to survive within macrophages³⁷ and ugtL is necessary for S. enterica to resist killing by host antimicrobial peptides³⁸, the absence of positive feedback would compromise S. enterica’s ability to proliferate within host tissues and cause disease. Moreover, S. enterica’s ability to grow in low Mg²⁺ is dependent on autoregulation of the PhoP/PhoQ system as removal of the PhoP box in the phoP promoter rendered S. enterica as defective as a phoP null mutant^34;35. In the bacterial species of the genus Bordetella, virulence is controlled by BvgA/BvgS, which is a more complex form of TCS termed phosphorelay. Remarkably, BvgAS is positively regulated, and this feedback regulation is essential for normal differential expression of the BvgAS-dependent genes¹⁵.

Our computational results indicate that positive feedback will likely affect not only the steady state (or the large-time dynamics) of a genetic regulatory system, but also the system dynamics for short and intermediate times (Fig. 5). This prediction has been verified in vivo for the PhoP/PhoQ TCS of S. enterica⁷. Notably, even when the influence of positive feedback on the steady state is negligible, abrogation of positive feedback can strongly feedback the transient dynamics, resulting in a prominent virulence phenotype⁷. Our model of transcription regulation with positive feedback (Eqs. (3)–(4)) suggests that strong effects of positive feedback on transient dynamics likely characterize many different types of genetic regulatory circuits involving positive feedback and two (one constitutive and one autoregulated) promoters (Fig. 3).

Positive feedback can impact genetic regulatory circuits in a variety of ways⁴. We can consider two main ways in which positively-autoregulated two-component systems, and genetic regulatory circuits in general, can be expressed. For circuits with a comparatively weak constitutive promoter, the effects of positive feedback are exhibited over a wide range of signal intensities, making positive feedback a major defining element of the circuit’s behavior. Alternatively, circuits with a stronger constitutive promoter, the specific positive-feedback-induced quantitative properties of regulation are displayed only when very strong signals are present. While it appears that the majority of positive feedback studies have focused mainly on the former type of regulation⁴, the biological relevance of the latter type of regulation is suggested by the analysis of phoPQ regulation in E. coli⁶. One can also envision situations, such as the generation of bacterial phenotypic heterogeneity, when positive feedback effects would be needed only in the cases of very strong inducing signals, which may signify, for example, the onset of extremely harsh environmental conditions. In such a situation, heterogeneity may contribute to the survival of the bacterial population³⁹. The occurrence of a specific type of functional organization may result from the action of evolutionary forces reflecting the niche(s) which the organism occupies²².

Detailed understanding of the functional role and properties of positive feedback in genetic circuits may enhance our ability to utilize such circuits as components of complex synthetic gene networks^30;40. Two-component signal transduction systems, due to their modular structure, may be particularly well-suited for applications in synthetic biology. The connection between the effects of positive feedback, promoter strengths, and activating signal intensities established in this work may facilitate the selection of molecular components, or “parts”, to guarantee the desired signal–response characteristics for engineered circuits⁴¹.

Methods

Mathematical modeling

Numerical solution of Eqs. (1)–(4) was performed in MATLAB 2009a (MathWorks, Natick, MA). To solve Eqs. (1)–(2) in the case of active autoregulated promoter (A > 0), we expressed the concentration of phosphorylated regulator in terms of the total regulator concentration from Eq. (1), and substituted the resulting expression into Eq. (2); the obtained equation was solved using the MATLAB function fzero. In the case of an inactive autoregulated promoter (A = 0), Eqs. (1)–(2) have an obvious explicit solution. Eqs. (3)–(4) were solved using the MATLAB function ode15s. The steady state of the dynamic positive feedback model (Eqs. (3)–(4)) was found by solving Eqs. (3)–(4) on increasing time intervals until convergence, in a similar way to the method described previously⁸.

Determination of gene expression

RNA isolation and transcription quantification were performed as follows: S. enterica cells were grown in N-minimal medium (pH 7.7) containing 10 mM Mg²⁺ (which is a repressing condition for PhoP/PhoQ ²⁷) to OD₆₀₀ ~ 0.5, and then shifted to media with different PhoP/PhoQ-inducing Mg²⁺ concentrations as described⁷. Measurements were performed in triplicate. The S. enterica strains used in this study are listed in Table S1, and the primers used are listed in Table S2 (see Supporting Information).