Abstract
Quantitative information regarding structurally disordered groups is crucial for a complete understanding of the relationship between structure, dynamics and function in biological macromolecules. Experimental analysis, however, of the positional distribution of disordered groups in the macromolecular frame is extremely difficult. While NMR order parameters, S2, for fixed-length bond vectors such as N-H and C-H are commonly used for investigations of conformational dynamics of macromolecules, these order parameters only provide angular information about internal motions and are totally insensitive to translational motions. Although analysis of S2 for bond vectors permit identification of disordered groups in macromolecules, this type of order parameter cannot provide any information about the distribution radii of disordered groups. Here we describe an NMR approach to directly determine the distribution radius of a disordered group independent of any structural knowledge. This approach makes use of order parameters for long variable-length vectors (including proton-paramagnetic center and proton-proton vectors) between a disordered group and a rigid portion of the macromolecule. We demonstrate the application of this formalism to paramagnetic relaxation enhancement vectors. In addition, the potential utility of the same formalism to 1H-1H cross-relaxation rates is considered as an alternative approach for analyzing the breadth of the positional distribution of disordered groups.
Introduction
Highly flexible or structurally disordered regions in macromolecules, such as surface exposed loops and disordered tails, often play a key role in function, for example by increasing the `capture radius'1,2 in macromolecular association.3–5 Experimental analysis, however, of the positional distribution of disordered groups in the molecular frame is challenging: time-resolved fluorescence energy transfer provides the distance distribution between two fluorophores6 but does not yield the distribution radius for a disordered group since both extrinsic fluorophores are attached to the macromolecule through mobile linkers; small angle X-ray scattering provides radial information at low resolution for the entire macromolecule7 but is not suitable for probing local structural disorder; crystallographic B factors can in principle provide the mean square displacement for each atom, but are either unavailable or unreliable for structurally disordered regions owing to very weak electron densities;8 finally, NMR order parameters (S2) for bond vectors (e.g. N-H and C-H) provide local dynamic and angular information on internal motions but are completely insensitive to translational motions.9 These issues have hindered experimental studies on the positional distributions of disordered groups in macromolecules, necessary to understand the interplay between structure, dynamics and function. Here we describe the formalism to directly determine the distribution radius of a disordered group by NMR independent of any structural knowledge. This approach makes use of order parameters for long variable-length vectors (including proton-paramagnetic center and proton-proton vectors) between a disordered group and a rigid portion of the macromolecule. An application to paramagnetic relaxation enhancement vectors is demonstrated.
Theory
The order parameter S2 for a vector whose length varies due to dynamics includes both angular and radial components, and can therefore provide information on the positional distribution. A general expression of S2 that that is applicable to both fixed- and variable-length vectors is given by:9–11
| [1] |
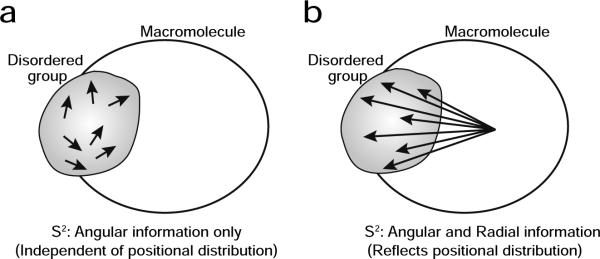
where <…> represents an ensemble average; r is the distance between the two atoms; are spherical harmonics given by and and θ and φ are polar angles for the vector within the molecular frame. For a fixed-length vector, the two contributions from r in Eq. [1] cancel out and only the angular component remains in S2. Consequently, order parameters for bond vectors located in a disordered group cannot provide information about the breadth of its positional distribution, although they can indicate that the group is indeed disordered (Figure 1a). On the other hand, S2 for variable-length vectors probed, for example, by paramagnetic relaxation (PRE) and nuclear Overhauser (NOE) enhancement measurements contain in principle both angular and radial components. If the vector is between an atom in a disordered region and another atom in a rigid portion of the molecule, the order parameter for the vector should reflect the positional distribution of the disordered group (Figure 1b). We take advantage of this feature to analyze the positional distribution of the disordered group.
Figure 1.
Different characteristics of the order parameters S2. S2 for (a) a short fixed-length vector (e.g. N-H or C-H bond) in a disordered group versus (b) a long variable-length vector (e.g. PRE or NOE interaction vector) between an atom in a disordered group and another atom in a rigid portion of the macromolecule. Each arrow represents a different state of the same vector in the ensemble.
Uniform distribution in a sphere model
To interpret the internal motions of variable-length vectors, we consider a model where the two atoms 1 and 2 of the vector in the molecular frame are independently and uniformly distributed in two separate spheres with radii RP and RN, respectively (Figure 2a). We refer to this as the `uniform distribution in a sphere' model (or `Sphere' model for short).
Figure 2.
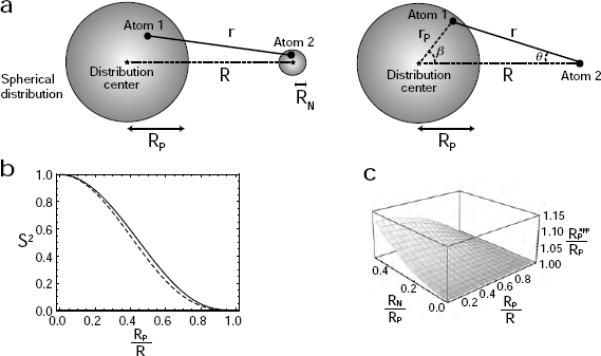
`Sphere' model for the internal motion of a variable-length vector in a macromolecular system. (a) Diagram depicting the DIS model in which atoms 1 and 2 are uniformly distributed in two separate spheres. On the left, atom 2 is distributed in a sphere of radius RN; on the right, the case with RN = 0 is shown. (b) Relationship between the order parameter S2 for the variable-length vector and the ratio RP/R for the `Sphere' model (solid line, RN = 0; dotted line, RN/RP = 0.4). (c) Impact of neglecting RN in the determination of RP. The ratio of the apparent RP (obtained from Eqs. [4], [7] and [8]) to the true value of RP as a function of RP/R and RN/RP is plotted.
We first consider the special case of RN = 0; that is Atom 2 is fixed at a point in the molecular frame. We define the following additional parameters: rP is the distance between Atom 1 and the center O of its distribution; θ is the Atom 1 – Atom 2 – O angle; and β is the Atom 1 – O – Atom 2 angle; r is the distance between atoms 1 and 2; and R is the distance between atom 2 and the center of the spherical distribution of atom 1. The radius RP of the sphere describing the distribution of atom 1 is assumed to be smaller than the center-to-center distance R. Since the ensemble < r−6> average for the surface of a sphere with radius rP is given by:
| [2] |
Using this result, the ensemble average <r−6> for a uniform distribution in a sphere with a radius RP is calculated to be:
| [3] |
Thus, the effective distance for the `Sphere' model with RN = 0 is given by:
| [4] |
where R is the distance between the center of the two spheres.
Because of the symmetry of the model, the ensemble average in Eq. [1] is non-zero only for m = 0. Hence,
| [5] |
where the Legendre polynomial P2(x) is given by (3x2−1)/2. Since cosθ = (R–rPcosβ)/r, the ensemble average 〈P2(cosθ)/r3〉 for a uniform distribution within a sphere of radius RP is given by:
| [6] |
S2 is obtained directly from Eqs. [3]– [6]:
| [7] |
It is important to note that S2 for this model provides purely radial information with respect to the spatial distribution of Atom 1. Eqs. [4] and [7] then permit the determination of the distribution radius RP from <r−6>−1/6 and S2 as:
| [8] |
If the distribution of Atom 1 is ellipsoidal, the apparent RP from this relation approximately corresponds to the average length of the semi-principal axes (see below).
Although RN = 0 was assumed for the above derivation, the use of Eqs. [4], [7] and [8] to estimate RP for RN ≠ 0 is still valid providing RN is substantially smaller than RP (Figures 2b and 2c). For RN ≠ 0, <r−6>−1/6 and S2 are approximated by and , respectively, providing the internal motions of the two atoms are uncorrelated. Figure 2b shows the relationships between S2 and RP/R. The solid line in this figure corresponds to a case with RN = 0, whereas the dotted line corresponds to a case with RN ≠ 0 and RN/RP = 0.4; these curves are very close to one another because of the relatively small scaling introduced by the dynamics of Atom 2. Figure 2c shows the ratio of the apparent RP obtained from Eqs. [4] and [7] to the true RP as a function of RP/R and RN/RP. Although the apparent value of RP is always larger than the true value of RP, the error is less than 10% for RN/RP < 0.4. Thus, Eqs. [4], [7] and [8] permit the accurate estimation of RP, if RN is substantially smaller than RP.
Considerations on the range of applicability of the formalism
Integration of Eqs. [2], [3] and [6] requires that RP < R. When the condition RP ≥ R occurs in the model shown in Figure 2a, the distance between the nucleus and paramagnetic center can be zero and r−6 would be infinity. Hence, a theoretical treatment is not feasible unless a lower limit for r is given. Such a case can be better dealt with using “pair correlation functions” originally proposed by Freed et al.12–14 Indeed, their theory takes the lower limit for r into consideration. However, if RP ≥ R, the lower limit of r governs the PRE data, and the calculation of the distribution radius from experimental PRE data is essentially impossible.
Considerations for non-spherical distributions
As described above, the distribution radius RP can be determined from S2 and <r−6>−1/6 with Eq. [8] assuming that the distribution of Atom 1 is spherical. What is the meaning of an apparent if we apply Eq. [8] for a non-spherical distribution? This question can readily be answered by using an N-state discrete jump model whose spatial distribution is arbitrary. For a discrete lattice model S2 and <r−6>−1/6 are given by:11
| [9] |
| [10] |
where r represents a vector between the Atom 1 and Atom 2; pi, the probability for the vector ri; and χij is the angle between vectors ri and rj. Here we consider the following two types of non-spherical distributions: an ellipsoidal distribution and a bimodal distribution. Other non-spherical/non-uniform distributions can be considered in the same manner.
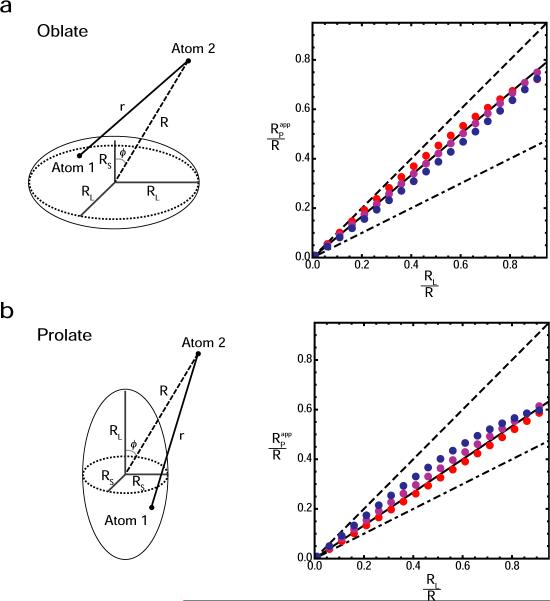
Numerical calculations of S2 and <r−6>−1/6 were carried out using uniformly distributed grid points in an oblate or prolate axially symmetric ellipsoid, and was calculated with Eq. [8]. As demonstrated in Figure 3, the numerical calculations indicate that the apparent value of RP is close to the average length of the three semi-principal axes (i.e. 2RL/3 + RS/3 and RL/3 + 2RS/3 for oblate and prolate ellipsoids, respectively.
Figure 3.
Calculated value of the apparent distribution radius RPapp for oblate (a) and prolate (b) axially symmetric ellipsoids. Five parameters are involved: the lengths of the axes RL and RS (RL > RS), the angle ϕ between the symmetry axis and the center – Atom 2 vector, the distance R between the center of an ellipsoid and Atom 2, and the distance r between Atom 2 and an arbitrary position in the ellipsoid. The order parameters S2 and effective distances <r−6>−1/6 were calculated using 3581 uniformly distributed grid points for an oblate ellipsoid and 3591 grid points for a prolate ellipsoid. Graphs display apparent RP/R values (red points, ϕ = 90°; magenta, ϕ = 45°; and blue, ϕ = 0°) as a function of the RL/R ratio for oblate and prolate ellipsoids with an anisotropy of RL/RS = 2.0. Dotted and dashed lines correspond to RL/R and RS/R, respectively. Solid lines represent (2RL/3 + RS/3)/R for an oblate ellipsoid, and (RL/3 + 2RS/3)/R for a prolate ellipsoid.
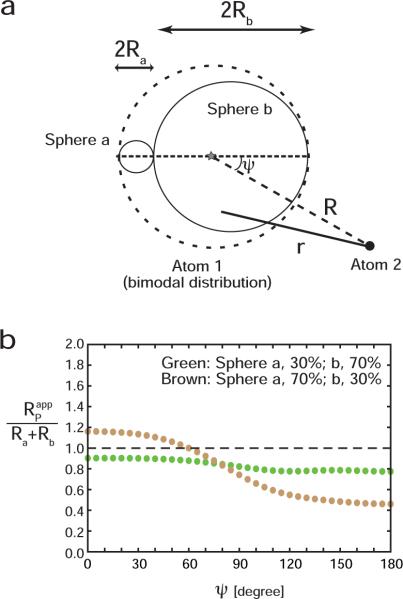
We also considered the bimodal distribution shown in Figure 4a. For this model, Atom 1 is uniformly distributed in two spheres `a' and `b' in contact with each other(radii Ra and Rb, respectively) with different probabilities (pa and 1− pa, respectively). The case with Rb/Ra = 3 and R = (Ra + Rb)/2 was examined. When pa = 0.3 (i.e. the probability for the smaller sphere is low), for this model is always smaller than Ra + Rb by ~20%, regardless of the position of Atom 2 (Green points in Figure 4b). When pa = 0.7 (i.e. the probability for the smaller sphere is high), can be larger or smaller than Ra + Rb, depending on the location of Atom 2, and the deviation from Ra + Rb is as large as 50% (brown points in Figure 4b). In such a case, accurate estimation of the breadth of the distribution from PRE order parameters and effective distances requires sampling of PRE vectors for nuclei at various locations.
Figure 4.
Calculated value of the apparent distribution radius RPapp for a bimodal distribution. (a) Model considered to represent the bimodal distribution. In this model, Atom 1 is distributed in two spheres `a' and `b' that are in contact each other (radii, Ra and Rb, respectively), whereas Atom 2 is fixed at a point defined by a distance R to the center of the symmetry axis for the bimodal distribution and an angle ψ between the vector of R and the symmetric axis of the distribution. The distribution of Atom 1 is uniform within each of the two spheres, but their probabilities are different. (b) Ratio of RPapp to Ra + Rb as a function of the angle ψ for a case with R = (Ra + Rb)/2 and Rb/Ra = 3. Plots were obtained with 3034 grid points in the bimodal distribution. The probability of populating sphere `a' was 30% for the green points and 70% for the brown points.
Determination of the distribution radius from PRE rates
The above formalism can readily be applied to PRE interaction vectors. The PRE rate Γ is the relaxation rate arising from magnetic dipole-dipole interactions between a nucleus and the unpaired electrons of a paramagnetic center, and is measured by taking the difference in the relaxation rates for the paramagnetic and diamagnetic states. We refer to the PRE rates for longitudinal and transverse magnetizations as Γ1 and Γ2, respectively. For paramagnetic systems with an isotropic electronic g-tensor (such as Mn2+, Gd3+, and nitroxide), the PRE rates are given by:
| [11] |
| [12] |
where s is the electron spin quantum number; g, the electron g-factor; γH, the 1H gyromagnetic ratio; μ0, the permeability of a vacuum; μB, the Bohr magneton; and ωH/2π, the Larmor frequency of the proton.15,16 The spectral density function J(ω) for a PRE interaction vector undergoing internal motions is given by:
| [13] |
where S2 is the order parameter for the PRE interaction vector (e.g. a Mn2+-1H vector); and r is the length of the PRE interaction vector (which is variable due to internal motion).17,18 The correlation times are given by and , where τr and τi are the correlation times for molecular rotation and internal motions, respectively, and τs is the electron relaxation time. For 1H nuclei in macromolecules, Γ1 and G2 are dominated by J(ωH) (where ω/2π is the 1H frequency) and J(0), respectively. These characteristics make it possible to directly determine values of S2 and <r−6>−1/6 for PRE interaction vectors in a structure-independent manner from PRE Γ1 and Γ2 rates at multiple magnetic fields by minimization of the χ2 function defined as:
| [14] |
where the superscripts calc and obs denote calculated and observed values; σ represents the experimental error for each PRE rate; and the indices j and k indicate different magnetic fields and 1H nuclei, respectively. For a system where the paramagnetic center (corresponding to Atom 1 in Figure 2a) is located in a structurally disordered group and the observed nuclei are located in a rigid portion of the macromolecule, the distribution radius RP can be calculated from <r−6>−1/6 and S2 using Eq. [8]. Simultaneously, Eqs. [4] and [7] yield the distance R given by
| [15] |
thereby providing paramagnetic center-proton distance restraints for structure calculations using a single average position for the paramagnetic center without the need to represent the mobile paramagnetic group by an ensemble of states.17
Practical considerations
From Eqs. [11]–[14] it can be seen that there are up to 4 unknown parameters per paramagnetic center-proton vector (τc, τi, S2 and <r−6>) but only two experimental observables. Although Γ2 is field independent, Γ1 varies with field, and hence, to ensure that the system is not underdetermined, it is essential to measure Γ1 at several magnetic fields over the frequency range characteristic of high resolution NMR (500 to 1000 MHz in 1H). The ratio of Γ1 rates at two magnetic fields is less than the square of the ratio of the magnetic fields, and therefore, considering experimental uncertainties in the measurements, it is advisable to use as wide a range of magnetic fields as is practically feasible. In the current work fields ranging from 500 to 800 MHz were employed.
We first consider the case where the paramagnetic label is located in a structurally disordered group and PREs are measured to protons in rigid regions of the proteins. The structurally disordered group can include not only the paramagnetic label itself but also neighboring residues if the label is attached to a residue located within a highly mobile region of the protein, such as a flexible loop. In the latter instance, the distribution radius of the paramagnetic center will reflect not only the intrinsic motion of the paramagnetic label but also the motion of the adjacent protein residues. (Note that mobile and rigid portions of the protein can readily be ascertained using conventional 15N relaxation measurements). To accurately determine the distribution radius of the paramagnetic center, Γ1 and Γ2 rates for as many paramagnetic center-proton vectors should be measured. The PRE data can then be fit using two approaches. In the first, the data are fit using Eq. [11]–[14] with the overall correlation time, τc, and the correlation time for internal motions, τi, treated as global parameters, and S2 and <r−6 > optimized for each PRE vector to yield corresponding values of Rp (Eq. [8]) and R (Eq. [15]). (A single value of τi is justified in this case since the dynamics of the PRE vectors are governed by the positional dynamics of the paramagnetic center.) From Figures 3 and 4b, it can be seen that the apparent value of Rp for a non-spherical distribution depends on the location of the observed proton. Consequently, it is easy to ascertain if the paramagnetic center is distributed in a highly non-spherical space, as the distribution of apparent Rp values would be much wider than that of a Gaussian distribution with a width corresponding to the experimental uncertainties of Rp. An alternative fitting procedure involves treating τc, τi and Rp as global parameters and only varying R for each PRE vector. In this instance, the spectral density function using in the χ2 function (Eq. [14]), can be readily derived from Eqs. [4], [7] and [13], and is given by:
| [16] |
If the PRE data can be well fit using the second procedure, and the distances R obtained using the two alternate fitting procedures are the same within experimental uncertainty, one can conclude that the spatial distribution of the paramagnetic center is essentially spherical (i.e. the deviations from a spherical distribution are small).
Next, we consider the case where the paramagnetic center is rigid and PREs are measured to protons in a disordered region(s). This situation is more complex since each paramagnetic center-proton vector will be characterized by its own internal correlation time τi, and hence τi can no longer be treated as a global parameter. (That being said, it would not be unreasonable to assume that τi values for adjacent residues would be correlated; hence, in a mobile loop, for example, the variation of τi as a function of residue position in the loop would not be expected to be random.) Likewise, each proton will be characterized by its individual distribution radius Rp. For this case, τc would still be treated as a global parameter, and the values of τi, R and Rp (using Eq. [16]) or τi, S2 and <r−6> (using Eq. [13]) would be optimized for each PRE vector. Given the number of unknowns, Γ1 rates would have to be measured at a minimum of three magnetic fields. Since the motional amplitudes of immediately adjacent residues will be correlated, the values of both R and Rp would be expected to change in small increments from the backbone of one residue to the next in the disordered region. Thus, in a disordered loop, maximal amplitudes would be predicted for the backbone of residues in the center of the loop becoming increasingly smaller as the residue approaches the rigid portion of the protein. Similarly, within a given residue, increased motional amplitudes would be expected as one advances towards the end of the side chain. Deviations from this behavior would only be expected when the conformational space sampled becomes significantly non-spherical. To a first approximation, it seems likely that the assumption of a spherical distribution will hold in most cases with the exception of motions involving a transition between two distinct conformational states (i.e. a two state jump).
Experimental
Preparation of the SRY/DNA-EDTA-Mn2+(Ca2+) complexes
U-[2H/15N]-labeled SRY was expressed and purified as described previously19 except that minimal medium containing D2O was used for deuteration. The 14-bp DNA duplex containing dT-EDTA chelating either Mn2+ or Ca2+ was prepared as described previously.17 The SRY/DNA-EDTA-Mn2+(or Ca2+) complexes were prepared by mixing the protein and DNA at a molar ratio of 1:1.2. The complexes were washed to remove excess Mn2+ (or Ca2+) as described.20,21 All buffers in this study were treated with Chelex-20 resin to remove all metal contamination. The NMR samples comprised 450-μl solutions of 0.3 mM SRY/DNA complex chelating either Mn2+ or Ca2+, 20 mM Tris•HCl (pH 6.8), 20 mM NaCl, and 7% D2O, sealed into Norell 5-mm NMR tubes. The low concentration for the protein/DNA complexes was chosen to avoid undesired so-called “solvent PRE” effects that arise from random molecular collisions.22
NMR experiments
NMR experiments were carried out using Bruker Avance spectrometers. Spectra were recorded at 308 K with cryogenic probes. PRE 1HN-Γ2 rates for the SRY/DNA-EDTA-Mn2+ complex were measured with a two-time-point approach as described.17,22 Errors in PRE Γ2 rates were estimated as described previously.22 For the 1HN-Γ1 measurements, we used the two-dimensional 1H-15N correlation experiment with a saturation recovery period prior to the HSQC scheme described in the following section. The Ca2+-chelated complex was used as the diamagnetic control for all PRE measurements. To identify 1H nuclei that undergo rapid (kex > 0.2 s−1) hydrogen exchange with water molecules,23 a 3D 15N-edited ROESY spectrum24 was measured with a 1H spin-lock of 30 ms duration at an rf strength of 4 kHz. 15N T1 and T2 relaxation times were measured for the SRY/DNA-EDTA-Ca2+ complex as described by Farrow et al.25 The rotational correlation time τr and the anisotropy of the rotational diffusion tensor were determined from the 15N T1/T2 ratios.26
Measurement of PRE 1HN-Γ1 rates
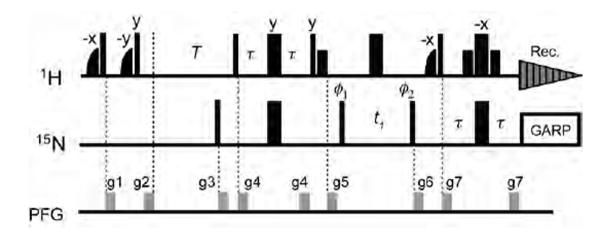
The measurement of PRE Γ1 rates at multiple magnetic fields is particularly important to obtain values for the order parameters S2 of the PRE interaction vectors. We measured the PRE Γ1 rates for the SRY/DNA-EDTA-Mn2+ complex using the saturation recovery 1H-15N HSQC-based experiment shown in Figure 5. Although the inversion recovery method for 1H longitudinal relaxation measurements generally offers higher precision than the saturation recovery,27 the saturation recovery method permits more rapid measurement of 1H longitudinal relaxation rates, since no magnetization recovery is required before the initial 1H pulse. For the present case involving a deuterated protein where 1HN-T1 relaxation times are very long, this feature is essential to permit completion of the experiment within a reasonable time frame. Delays for the saturation recovery were 0.005, 0.20, 0.60, 0.005, 0.20, 0.60, 1.20, 2.00, 3.00, 4.00, and 5.00 s at 600 MHz; and 0.005, 0.20, 0.60, 1.20, 2.00, 3.00, 4.20, and 5.60 s at 800 MHz. A phenomenological longitudinal relaxation rate R1 is obtained by fitting the signal intensities to I(T)=−I(∞)exp(−R1T) + I(∞). The PRE1HN-Γ1 rates were determined as R1,para - R1,dia, where R1,para and R1,dia are the longitudinal relaxation rates for paramagnetic and diamagnetic states, respectively. Errors in Γ1 rates were estimated as , where σR1,para and σR1,dia are the errors in the 1H R1 rates for the paramagnetic and diamagnetic states, respectively. Data for protons that exhibit non-single-exponential behavior due to rapid hydrogen exchange (or possibly due to 1H-1H cross relaxation) were excluded, and consequently, the total number of Γ1 data points used in the analysis is less than the number of Γ2 data points.
Figure 5.
Pulse sequence for the saturation recovery experiment for measurement of PRE 1HN-Γ1 rates for 2H-labeled proteins. The initial two pairs of shaped and rectangular 1H pulses along with pulse field gradients kill all 1HN magnetization, which recovers during the delay T and is then detected using a water-flip-back 1H-15N HSQC pulse scheme.28 Two-dimensional spectra with different values of T are recorded in an interleaved manner. Phases are along × unless indicated otherwise. Thin and bold lines represent rectangular 90° and 180° pulses, respectively. Small bold 1H pulses represent water-selective rectangular 90° pulses (1.4 ms). Half-bell shapes represent 1H half-Gaussian pulses selective to water (2.1 ms). The delay τ is 2.3 ms. Phase cycling is as follows: ϕ1 = [x, −x]; f2 = [2x, 2(−x)]; receiver = [x, 2(−x), x]. Quadrature detection for t1 dimension was carried out with phase incrementation of ϕ1 in a States-TPPI manner.
χ2 minimization
Non-linear least-squares fitting was carried out using the Levenberg-Marquardt algorithm, and errors in the calculated parameters were estimated using the Monte-Carlo method.
Structure-based calculation of the positional distribution of EDTA-Mn2+ in the SRY/DNA-EDTA-Mn2+ complex
The distribution of the EDTA-Mn2+ group was also examined by high-temperature simulated annealing calculations carried out using the Xplor-NIH molecular structure determination package.29 The target function for simulated annealing comprised only terms for covalent geometry (bond, angles, impropers) and van der Waals interactions (in the form of a quartic van der Waals repulsion term). No pseudo-energy terms for experimental data were employed. Topology and parameters for the EDTA-Mn2+ group were set as described in the Supporting information of Iwahara et al.17 The conformation of the linker between the EDTA-Mn2+ group and the thymine base was randomized during the high temperature stage (3000 K), followed by slow cooling to 25 K. In this calculation, only the dT-EDTA-Mn2+ group (from the linker onwards) was allowed to move while the other parts of the complex were kept fixed. 400 different conformations of dT-EDTA-Mn2+ were computed.
Results and Discussion
SRY/DNA complex and PRE rates
As a model system to test the method described in the Theory section, we determined the distribution radius of the EDTA-Mn2+ paramagnetic group covalently attached to a thymine base21,30 in the SRY/DNA complex (Figure 6a) from PRE rates without recourse to any structural information. The EDTA-Mn2+ group is covalently attached to a thymine base in this complex through a flexible linker consisting of five rotatable bonds (Figure 6a), and is therefore disordered with respect to the core of the protein/DNA complex. A previous study on the same SRY/DNA-EDTA-Mn2+ complex system showed that the PRE rates for this system are fully consistent with the structure of the complex.17 Although it is known that low-population intermediates in macromolecular association can make PRE rates inconsistent with the structures of specific complexes,20,31–33 such effects of intermediates are negligible for the SRY/DNA complex. Thus this complex represents an ideal model system to test the new method.
Figure 6.
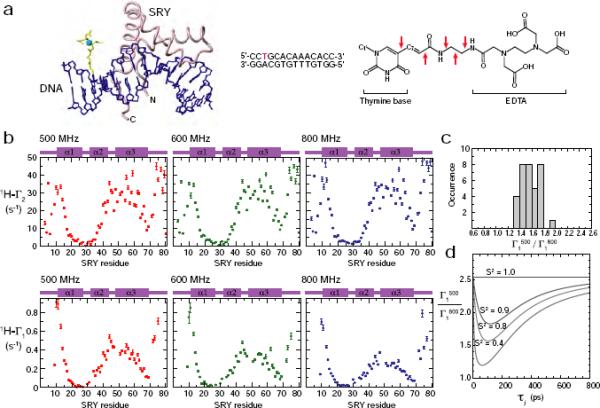
PRE measurements for the SRY/DNA complex at multiple fields. (a) Structure of the SRY/DNA-EDTA-Mn2+ complex.17 The EDTA-Mn2+ group (yellow/cyan) is tethered to a thymine base (red in the sequence) in the 14-bp DNA duplex. The chemical structure of T-EDTA is also shown (asterisks, coordination sites; arrows, rotatable bonds in the linker). (b) PRE 1HN-Γ1 and Γ2 rates measured at three magnetic fields. (c) Histogram of the ratio of PRE 1HN-Γ1 rates measured at 500 and 800 MHz. (d) Theoretical dependence of Γ1500/Γ1800 ratio on the order parameter S2 and the internal motion correlation time τi for a Mn2+-1H vector.
PRE 1HN-Γ1 and 1HN-Γ2 rates were measured for U-[2H/15N-labeled SRY bound specifically to a 14-bp DNA duplex conjugated to EDTA-Mn2+ (Figure 6b) at three high magnetic fields: 11.7, 14.0, and 18.7 Tesla (1H-frequencies, 500, 600, and 800 MHz, respectively). Deuterated SRY was employed to obtain higher precision for the PRE measurements and to minimize the effect of 1H-1H cross relaxation on the PRE Γ1 rates.34 Figure 6b show the measured 1HN-Γ1 and 1HN-Γ2 rates for SRY backbone amide groups in the complex. Since the PRE is proportional to <r−6>, residues that are close to Mn2+ exhibit large values of 1HN-Γ1 and 1HN-Γ2.
The PRE 1HN-Γ2 rates display negligible field dependence. At the three different magnetic fields, most nuclei exhibit 1HN-Γ2 values that differ only within a factor of two of the experimental errors. As described previously,22 this result indicates that the contribution of Curie-spin relaxation to Γ2 is negligible and that the field-dependence of τc is minimal in this magnetic field range. The field-independent nature of τc is reasonable because, for EDTA-Mn2+, the electron relaxation due to collisional modulation of the zero-field splitting (ZFS) tensor that can cause field-dependence of τs−1 should occur with a rate of 104 – 105 s−1 at 11.7 – 18.7 Tesla, judging from the results of a previous low-field NMR study.35 Although the actual electron relaxation rate τs−1 can be substantially larger than this estimate due to the contribution from vibrational modulation of the Mn2+ ZFS tensor,36 the electron relaxation due to this mechanism is essentially field-independent, and therefore, the PRE correlation time τc, defined as (τr−1 + τs−1)−1, should be virtually field-independent for the present case.
In contrast, the PRE 1HN-Γ1 rates display significant field dependence. Figure 6c shows a histogram of Γ1(500 MHz)/Γ1(800 MHz) ratios for residues with Γ1 > 0.1 s−1 at both fields: the average ratio is 1.70±0.15. If PRE vectors are static with S2 = 1.0, the Γ1(500 MHz)/Γ1(800 MHz) ratios for the present case (with ωHτc >> 1) should be 2.56, which is considerably larger than the observed values. Even if the contribution from collisional modulation of zero field splitting tensor35,37 is non-negligible in τs−1, the field-dependence of τs−1 should make the ratio larger rather than smaller. Dynamics of PRE vectors, however, on the pico- to nanosecond timescale with S2 < 1.0 makes the ratio considerably smaller than 2.56 (Figure 6d). Thus, the observed Γ1(500 MHz)/Γ1(800 MHz) ratios clearly indicate that the PRE vectors are dynamic in this system.
Although it is known that the unpaired electron spin density delocalized to the 2pz orbital can render the <r−6> dependence of the PRE rate invalid for redox-active systems such as electron transfer proteins,38–40 Eqs. [11–13] were experimentally validated for the SRY/DNA-EDTA-Mn2+ complex in our previous study.17 Thus, these equations were used for subsequent analysis.
Order parameters and effective distances for PRE vectors
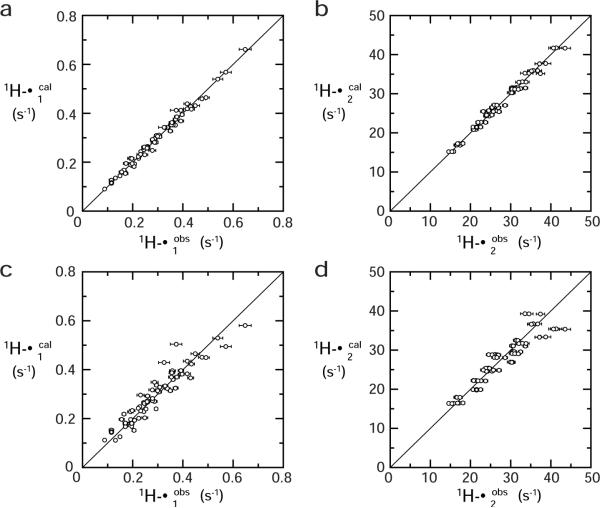
The order parameters S2 and effective distances <r−6>−1/6 for the PRE vectors were determined via non-linear least-squares fitting (cf. Eq. [14]). For the calculation, we used a total of 132 PRE rates for 22 1HN nuclei that are located in structurally rigid portions of the complex (as evidenced by 15N relaxation) and satisfy the following four criteria: (i) Γ1 > 0.1 s−1; (ii) Γ2 > 15 s−1; (iii) slow hydrogen exchange with water with a rate kexwater < ~0.2 s−1); and (iv) single-exponential recovery of magnetization in the saturation recovery experiments for Γ1 measurements. The latter two conditions are important for accurate measurement of Γ1 rates. Condition (iii) was verified using a 3D 15N-separated ROE spectrum, in which H2O-exchange cross peaks appear with opposite sign to ROE cross-peaks, thereby permitting permit identification of HN atoms that undergo rapid hydrogen exchange.24. Three fitting calculations were performed and the results are summarized in Table 1. First, using Eqs. [11]–[14], the order parameter S2 and effective distance <r−6>−1/6 were optimized for each PRE vector, while the PRE correlation time τc (constrained by the relationship τc ≤ τr which always holds from the definition of τc) and the internal motion correlation time τi were treated as global parameters. The final value of the reduced χ2 (i.e. χ2 per degree of freedom) is 2.5, indicating a reasonably good fit (Table1, Fitting Procedure 1). This is also clear from the correlation plot of observed versus calculated Γ1 (Figure 7a) and Γ2 (Figure 7b) rates. The rotational correlation time τr determined from 15N T1 and T2 relaxation times is 8.5 ns (with a diffusion anisotropy of 1.1). The values of τc and τi obtained from the PRE data are 7.2±0.9 ns and 0.20±0.02 ns, respectively. The values of S2 range from 0.65 to 0.84, and the effective distances <r−6>−1/6 from 20.8 Å to 24.2 Å (Table 2). A histogram of the distribution radius RP for the EDTA- Mn2+ group calculated from S2 and <r−6>−1/6 (using Eq. [8]) for each Mn2+–1H vector is shown in Figure 8a. The average value of RP is 6.9±0.8 Å. Considering that a typical backbone root mean square deviation in molecular dynamics simulations of proteins is 1–2 Å41, the error in RP arising from neglecting RN is estimated to be less than 3% from Figure 2c, which is well below the experimental uncertainty.
Table 1.
Models used for nonlinear least-squares optimizationa and their statistics.
| J(ω) | Globalb | Individualc | degrees of freedom | reduced χ2d | AICe | |
|---|---|---|---|---|---|---|
| Fitting 1 (Eq. [13]) | τc, τi | S2, <r−6>−1/6 | 86 | 2.7 | 326.6 | |
| Fitting 2 (Eq. [16]) | τc, τi Rp | R | 107 | 12.6 | 1401.2 | |
| Fitting 3 (Eq. [17]) | τ c | <r−6>−1/6 | 109 | 31.8 | 3511.4 |
Minimization of the χ2 function defined by Eq. [14]. PRE Γ1and Γ2 data measured for 22 different Mn2+-1H vectors at three magnetic fields were used. Total number of square terms is 132 (= 22 × 2 × 3).
Globally optimized parameter(s).
Parameter(s) individually optimized for each PRE vector.
χ2per degree of freedom.
Akaike's Information Criterion. AIC = χ2 + 2k, where k is the number of optimized parameters.
Figure 7.
Correlation between calculated and observed PRE rates. (a, b) Fitting Procedure 1. (c, d) Fitting Procedure 2. Statistics are given in Table 1.
Table 2.
Values of the order parameter S2 and the effective distance <r−6>−1/6 for Mn2+-1HN vectors determined by non-linear least-squares fitting, and values of the center distances R and the distribution radii RP calculated from S2 and <r−6>−1/6 using Fitting Procedure 1.a
| 1HN b | S2 | <r−6>−1/6(Å) | R(Å) | RP(Å) |
|---|---|---|---|---|
| I13 | 0.65 ± 0.04 | 20.6 ± 0.3 | 22.1 ± 0.5 | 8.0 ± 0.7 |
| V14 | 0.68 ± 0.04 | 21.9 ± 0.3 | 23.3 ± 0.5 | 8.1 ± 0.7 |
| W15 | 0.73 ± 0.04 | 22.9 ± 0.4 | 24.1 ± 0.6 | 7.6 ± 0.8 |
| S16 | 0.74 ± 0.04 | 23.8 ± 0.4 | 25.0 ± 0.6 | 7.7 ± 0.8 |
| Y41 | 0.73 ± 0.04 | 22.3 ± 0.3 | 23.5 ± 0.5 | 7.4 ± 0.7 |
| W43 | 0.71 ± 0.04 | 21.9 ± 0.3 | 23.2 ± 0.5 | 7.7 ± 0.7 |
| K44 | 0.71 ± 0.04 | 20.8 ± 0.3 | 22.0 ± 0.5 | 7.2 ± 0.7 |
| M45 | 0.72 ± 0.04 | 21.3 ± 0.3 | 22.5 ± 0.5 | 7.3 ± 0.7 |
| L46 | 0.75 ± 0.04 | 21.5 ± 0.3 | 22.5 ± 0.5 | 6.9 ± 0.7 |
| W52 | 0.78 ± 0.03 | 21.6 ± 0.3 | 22.5 ± 0.5 | 6.4 ± 0.7 |
| F54 | 0.73 ± 0.04 | 21.9 ± 0.3 | 23.1 ± 0.5 | 7.3 ± 0.7 |
| F55 | 0.78 ± 0.04 | 21.0 ± 0.3 | 21.9 ± 0.5 | 6.1 ± 0.7 |
| Q56 | 0.76 ± 0.04 | 21.3 ± 0.3 | 22.3 ± 0.5 | 6.7 ± 0.7 |
| E57 | 0.76 ± 0.04 | 22.4 ± 0.4 | 23.5 ± 0.5 | 7.0 ± 0.7 |
| A58 | 0.78 ± 0.03 | 21.6 ± 0.4 | 22.6 ± 0.5 | 6.4 ± 0.7 |
| Q59 | 0.82 ± 0.03 | 20.8 ± 0.3 | 21.5 ± 0.5 | 5.5 ± 0.7 |
| K60 | 0.77 ± 0.03 | 22.3 ± 0.4 | 23.3 ± 0.5 | 6.7 ± 0.7 |
| L61 | 0.78 ± 0.04 | 22.8 ± 0.4 | 23.8 ± 0.6 | 6.6 ± 0.7 |
| A63 | 0.83 ± 0.03 | 22.0 ± 0.4 | 22.7 ± 0.5 | 5.6 ± 0.7 |
| M64 | 0.73 ± 0.04 | 24.1 ± 0.4 | 25.4 ± 0.6 | 8.0 ± 0.8 |
| H65 | 0.84 ± 0.03 | 24.2 ± 0.4 | 24.9 ± 0.6 | 5.9 ± 0.8 |
| R66 | 0.84 ± 0.03 | 23.3 ± 0.4 | 24.0 ± 0.6 | 5.8 ± 0.7 |
Values were obtained via minimization of the χ2 function defined by Eq. [14] together with Eq. [13]. The distribution radii (RP) and center distances (R) were calculated using Eqs. [8] and [15], respectively. The optimized values of the correlation times τc and τi are 7.2 ± 0.9 ns and 0.20 ± 0.02 ns, respectively. bAmide protons that satisfied the four criteria described in the main text. Numbering of SRY residues is according to Murphy et al.19
Figure 8.
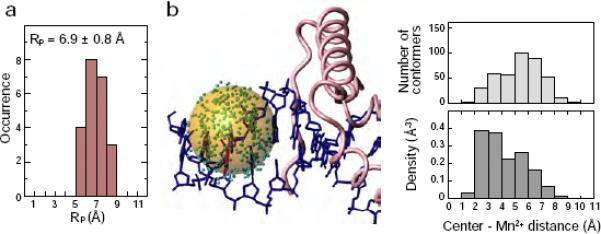
The distribution radius Rp of the EDTA-Mn2+ group in the SRY/DNA complex. (a) Histogram of RP calculated from S2 and <r−6>−1/6 for 22 Mn2+-1H vectors in the SRY/DNA-EDTAMn2+ complex. (b) Mn2+ distribution obtained by structure-based simulated annealing calculations. In the left panel of (b), the positions of Mn2+ for 400 different conformers are shown in green. The transparent orange sphere, with its origin placed at the center of the distribution, is drawn with a radius of 6.9 Å, corresponding to the average value of RP determined by the structure-independent method. In the right-hand panel of (b), a histogram of the distance from the center of the distribution to individual Mn2+ positions (top) and the density (bottom) of the Mn2+ for the 400 conformers (obtained by dividing the number of conformers by the volume of a shell with 1 Å thickness) are shown.
We also carried out a second fitting procedure in which a single, global value of RP was optimized in the non-linear least squares fit using Eq. [16]. The resulting reduced χ2 value is 12.8 (Table 1, Fitting Procedure 2), indicating that the quality of the fit is not quite as good as that obtained using Fitting Procedure 1 (Eq. [13]). This is borne out from the correlation plot of observed versus calculated Γ1 and Γ2 rates (Figures 7c and d, respectively), although the correlation is still good, except for a couple of outliers in the Γ1 correlation plot (Figure 7c). The value of Akaike's Information Criterion (AIC), however, for Fitting Procedure 1 is far lower than that for Fitting Procedure 2, implying that the positional distribution of the EDTA-Mn2+ is not perfectly symmetric (Table 1). The global value of RP obtained using Fitting Procedure 2 is 7.4±0.6 Å, which is still within one standard deviation of the mean value of 6.9±0.8 Å for Rp obtained using Fitting Procedure 1.
The values of the center distances R obtained for fitting procedure 2 are listed in Table 3. The rms difference between the values of R obtained using Fitting Procedures 1 and 2 is only 0.7 Å, which represents a difference of less than 4% in the values obtained using the two fitting procedures. This indicates that robust and accurate values of the distances R from 1H nuclei to the center average position of the paramagnetic center (in this instance Mn2+) can be obtained using the formalism and procedures described here. This has important practical implications since these distances can be used directly in structure calculations without the need to represent the mobile paramagnetic group by an ensemble of states and refine directly against the PRE data.
Table 3.
| 1HN | R [Å] |
|---|---|
| I13 | 22.3 ± 0.5 |
| V14 | 23.5 ± 0.5 |
| W15 | 24.5 ± 0.5 |
| S16 | 25.4 ± 0.6 |
| Y41 | 24.0 ± 0.5 |
| W43 | 23.5 ± 0.5 |
| K44 | 22.6 ± 0.5 |
| M45 | 23.0 ± 0.5 |
| L46 | 23.2 ± 0.5 |
| W52 | 23.4 ± 0.5 |
| F54 | 23.6 ± 0.5 |
| F55 | 22.9 ± 0.5 |
| Q56 | 23.1 ± 0.5 |
| E57 | 24.1 ± 0.5 |
| A58 | 23.5 ± 0.5 |
| Q59 | 22.7 ± 0.5 |
| K60 | 24.1 ± 0.5 |
| L61 | 24.6 ± 0.6 |
| A63 | 23.8 ± 0.5 |
| M64 | 25.8 ± 0.6 |
| H65 | 25.8 ± 0.6 |
| R66 | 25.0 ± 0.6 |
Values were obtained via minimization of the χ2 function defined by Eq. [14] together with Eq. [16] (Fitting Procedure 2 in Table 1). Values of the correlation times τc and τi were calculated to be 7.7 ± 0.8 ns and 0.21 ± 0.01 ns, respectively. The distribution radius RP, defined as a global parameter, was calculated to be 7.4 ± 0.6 Å.
As a control, we also carried out a fit using the spectral density function:
| [17] |
which corresponds to the case where S2 = 1; that is no internal motion for the paramagnetic label. The resulting reduced χ2 has a value of 31.8 (Table 1, Fitting Procedure 3), indicating, as expected, that Eq. [17] is inappropriate in the present instance owing to dynamics of the Mn2+–1H vectors (i.e. S2 ≠ 1).
The value of Rp obtained from the structure-independent method is fully consistent with the distribution obtained from structure-based high-temperature simulated annealing calculations incorporating covalent geometry and van der Waals terms allowing the EDTA-Mn2+ group to move while keeping the rest of the complex fixed (Figures 8b and c). This result suggests that the real distribution of the disordered EDTA-Mn2+ group in the molecular frame of the SRY/DNA complex is as wide as that predicted from structure-based computations. Equally importantly, the reasonable value of the distribution radius obtained for this model system provides evidence that the structure-independent method works.
Considerations for obtaining information about distribution radii of disordered groups from 1H-1H cross-relaxation rates
Here we briefly consider how and under what circumstances one might obtain information about the distribution radii of disordered groups in macromolecules from 1H-1H cross-relaxation rates using the formalism presented in this paper. The cross-relaxation rates for the 1H-1H NOE (σNOE) and ROE (σROE) are given by:42
| [18] |
| [19] |
where the spectral density function JHH(ω) is given by:10,11
| [20] |
and τe = (τr−1 + τi−1)−. Note that Eqs. [13] and [20] differ in that the correlation times in Eq. [13] contain the electron correlation time τs. Using Eqs. [4] and [7], together with Eqs. [18]–[20], one can consider the relationship between the distribution radius RP and cross-relaxation rates for the `Sphere' model.
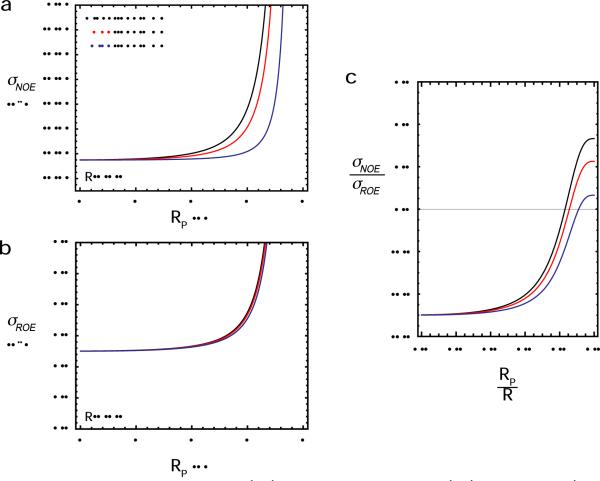
For 1H-1H vectors between protons in relatively rigid portions of a macromolecule, both NOE and ROE cross-relaxation rates are dominated by the spectral density function JHH(0) = <r−6>S2τr. Given that R−6 = <r−6>S2 for the `Sphere' model (cf. Eqs. [4] and [7]), 1H-1H cross relaxation rates are independent of the distribution radius RP, under conditions where the JHH(0) term predominates. In this limit, it is impossible to determine RP from 1H-1H cross-relaxation rates. From the perspective of structural analysis, the relationship JHH(0) = R−6τr in this limit is extremely useful because it means that the center distance R can be determined without any influence of dynamics.
For 1H-1H vectors, however, between a disordered group and a rigid portion of the macromolecule, the JHH(2ωH) term in Eq. [18] can be non-negligible, and the field-dependence of NOE cross-relaxation can be quite significant. As shown in Figure 9, this occurs when RP and R are comparable. In such a case, the 1H-1H cross-relaxation rates σNOE and σROE are dependent on RP, and, therefore, permit one to derive information about the positional distribution of the disordered group. For a 1H-1H pair that exhibits a field-dependent σNOE, a χ2 function containing square terms for σNOE and σROE (analogous to Eq. [14]) can be used to determine the order parameter S2 and effective distance <r−6>−1/6, and hence RP. Since the overall rotational correlation time τr in Eq. [20] can readily be obtained from other data (e.g. 15N T1 and T2 relaxation data), σNOE and σROE rates at only two magnetic fields are sufficient to determine τi, S2 and <r−6>−1/6 (and RP from the latter two). If the value of τi can also be obtained from other data (for example, for a 1H-1H vector between a disordered arginine guanido group and a rigid backbone amide proton, 15Nε relaxation data can provide the correlation time for the internal motion of the 1Hε-1HN vector), σNOE and σROE rates at a single magnetic field should be sufficient to determine RP. For such a case, the σNOE /σROE ratio provides a very useful indicator (Figure 9c): if the ratio is significantly larger than −0.5, the distribution radius RP can be determined using this approach.
Figure 9.
Effect of the distribution radius on 1H-1H cross-relaxation rates. (a) 1H-1H NOE and (b) 1H-1H NOE cross-relaxation rates as a function of the distribution radius RP for the `Sphere' model with R = 4 Å and RN = 0 Å. The curves were obtained using Eqs. [18]–[20], together with Eqs. [4] and [7]. (c) Ratio of NOE to ROE cross-relaxation rates as a function of RP/R. For all panels, calculations at 1H frequencies of 500, 700, and 800 MHz (shown in black, red, and blue, respectively) were carried out with correlations times of τr = 9 ns and τi = 0.2 ns.
Although spin-diffusion effects in both NOE and ROE experiments and undesirable TOCSY transfer in the ROE experiment may potentially hinder accurate measurement of 1H-1H cross-relaxation rates, these problems can readily be overcome for 1H-1H pairs between labile protons (e.g. backbone and side-chain N-H protons) by using perdeuterated proteins in which the replacement of non-exchangeable protons by deuterons removes the spin-diffusion and TOCSY transfer pathways. Indeed, accurate measurement of 1H-1H cross-relaxation rates on a highly deuterated protein has recently been demonstrated.43
Concluding remarks
Although the proof-of-principle application presented here relates to PRE vectors in which the paramagnetic center is located in a disordered group and the observed 1H nuclei are in rigid portions of the molecule, the opposite situation in which the paramagnetic center is at a fixed point and the 1H nuclei are located in disordered groups, can also be analyzed to determine the distribution radius of disordered or highly mobile regions of a macromolecule. From this perspective, future applications to disordered groups on engineered proteins with an immobilized paramagnetic group44–46 (M.R. Feissner and W.L. Hubbell, pdb code 1ZUR) or on metal-binding proteins are of interest. In addition, large-scale interdomain motions can also be analyzed using a highly mobile paramagnetic label, as in the present case, under conditions where the distribution radius of the paramagnetic label is much smaller than that of the interdomain motion. Such a situation would apply when two domains are connected by highly flexible linkers. The same is true with regard to the analysis of the distribution radius of a disordered loop containing the paramagnetic label. Finally, the formalism presented here and described by Eqs. [4] and [7] can be incorporated into equations for NOE/ROE cross-relaxation rates and simulations predict that it is also possible in principle to obtain information about the distribution radii of disordered groups such as surface side-chains from cross-relaxation rates for 1H-1H pairs between a disordered group and a rigid portion of the macromolecule.
In addition to its utility in probing distribution radii of disordered groups, the method presented here can also be used to provide paramagnetic center-proton distances for structure calculations. Previously, we had introduced a multi-conformer representation of the paramagnetic group together with a theoretical framework and computational strategy to directly refine against PREs arising from a flexible paramagnetic group.17 Since the method presented here provides the center distances R from the center of a spherical distribution of the paramagnetic center to the observed nuclei (cf. Eq. 15, and Tables 2 and 3), PRE-based structure calculations could be carried out using a single conformer representation of the paramagnetic group together with a standard pseudo-potential term for the distance restraints29,47 and no special treatment for the paramagnetic group, providing the paramagnetic center is distributed approximately uniformly within a sphere. (For PREs involving methyl groups, the conventional “center-average' for NOE-derived interproton distance restraints would be used.29,47) In most circumstances a square-well potential would be employed with a range corresponding to say the 5–95% confidence limits for the values of R determined from the fits to the Γ1 and Γ2 data (cf. Eqs. [11], [12] and [14] combined with Eqs. [13] and [15] or Eq. [16]). This approach can be advantageous since it renders structure calculations simpler, faster and more straightforward. In addition, the convergence properties of distance restraints in simulated annealing calculations are superior to that of PRE Γ2 restraints. However, there are also some disadvantages: first, extraction of the center distances R require a far larger number of datasets at multiple magnetic fields and is therefore time-consuming (in the present case, the total experimental time for the Γ1 measurements at three magnetic field strengths was ~15 days); second, measurement of accurate Γ1 data is more difficult than Γ2, and further Γ1 is much more sensitive to internal motions, cross-correlation effects and exchange with water than Γ2;17 third, the center distances R are strictly only valid for spherical distributions (anisotropic distributions could be handled by simply increasing the error bounds on the distance restraints, but in the case of bimodal distributions the estimates of R may contain significant errors).
In conclusion, we have demonstrated the NMR strategy and formalism required to obtain the distribution radii of disordered groups in macromolecules in a structure-independent manner using PRE data, which has been very difficult to achieve by any other biophysical experimental method. This new approach can provide new insights into inter-domain dynamics and local disorder of proteins, which are important for understanding the role of dynamics in protein function. In addition, the same approach can be used to obtain distance restraints from the center of the distribution of a mobile paramagnetic group to protons of a macromolecule. Although the present application was demonstrated for the relatively small (~18 kDa) SRY-DNA complex, recent work using methyl TROSY experiments to measure PREs for the 180 kDa proteoasome complex48 indicates that the method should be applicable to systems larger than 100 kDa.
Acknowledgments
We thank Dr. Attila Szabo for stimulating discussions and for originally pointing out to us that <r−6>S2 = R−6 to order R−10 for any spherical distribution centered on R. This work was supported by Grant H-1683 from the Welch Foundation (to J.I.), Grant MCB-0920238 from the National Science Foundation (to J.I.), the intramural research program of the National Institute of Diabetes and Digestive and Kidney Diseases, NIH (to G.M.C.) and the AIDS Targeted Antiviral Program of the Office of the Director of the NIH (to G.M.C.).
References
- (1).Shoemaker BA, Portman JJ, Wolynes PG. Proc Natl Acad Sci U S A. 2000;97:8868–8873. doi: 10.1073/pnas.160259697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (2).Levy Y, Cho SS, Onuchic JN, Wolynes PG. J Mol Biol. 2005;346:1121–1145. doi: 10.1016/j.jmb.2004.12.021. [DOI] [PubMed] [Google Scholar]
- (3).Spolar RS, Record MT., Jr. Science. 1994;263:777–784. doi: 10.1126/science.8303294. [DOI] [PubMed] [Google Scholar]
- (4).Wright PE, Dyson HJ. Curr Opin Struct Biol. 2009;19:31–38. doi: 10.1016/j.sbi.2008.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (5).Gsponer J, Babu MM. Prog Biophys Mol Biol. 2009;99:94–103. doi: 10.1016/j.pbiomolbio.2009.03.001. [DOI] [PubMed] [Google Scholar]
- (6).Lakowicz JR. Principles of fluorescence spectroscopy. 3rd ed. Springer; New York: 2006. [Google Scholar]
- (7).Bernado P, Mylonas E, Petoukhov MV, Blackledge M, Svergun DI. J Am Chem Soc. 2007;129:5656–5664. doi: 10.1021/ja069124n. [DOI] [PubMed] [Google Scholar]
- (8).Kuriyan J, Petsko GA, Levy RM, Karplus M. J Mol Biol. 1986;190:227–254. doi: 10.1016/0022-2836(86)90295-0. [DOI] [PubMed] [Google Scholar]
- (9).Lipari G, Szabo A. J Am Chem Soc. 1982;104:4546–4559. [Google Scholar]
- (10).Olejniczak ET, Dobson CM, Karplus M, Levy RM. J Am Chem Soc. 1984;106:1923–1930. [Google Scholar]
- (11).Brüschweiler R, Roux B, Blackledge M, Griesinger C, Karplus M, Ernst RR. J Am Chem Soc. 1992;114:2289–2302. [Google Scholar]
- (12).Hwang LP, Freed JH. J. Chem. Phys. 1975;63:4017–4025. [Google Scholar]
- (13).Freed JH. J. Chem. Phys. 1978;68:4034–4037. [Google Scholar]
- (14).Xue Y, Podkorytov IS, D.K. R, Benjamin N, Sun H, Skrynikov NR. Protein Sci. 2009;18:1401–1424. doi: 10.1002/pro.153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (15).Bloembergen N, Morgan LO. J Chem Phys. 1961;34:842–850. [Google Scholar]
- (16).Solomon I. Phys Rev. 1955;99:559–565. [Google Scholar]
- (17).Iwahara J, Schwieters CD, Clore GM. J Am Chem Soc. 2004;126:5879–5896. doi: 10.1021/ja031580d. [DOI] [PubMed] [Google Scholar]
- (18).Clore GM, Iwahara J. Chem Rev. 2009;109:4108–4139. doi: 10.1021/cr900033p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (19).Murphy EC, Zhurkin VB, Louis JM, Cornilescu G, Clore GM. J Mol Biol. 2001;312:481–499. doi: 10.1006/jmbi.2001.4977. [DOI] [PubMed] [Google Scholar]
- (20).Iwahara J, Clore GM. Nature. 2006;440:1227–1230. doi: 10.1038/nature04673. [DOI] [PubMed] [Google Scholar]
- (21).Iwahara J, Anderson DE, Murphy EC, Clore GM. J Am Chem Soc. 2003;125:6634–6635. doi: 10.1021/ja034488q. [DOI] [PubMed] [Google Scholar]
- (22).Iwahara J, Tang C, Clore GM. J Magn Reson. 2007;184:185–195. doi: 10.1016/j.jmr.2006.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (23).Grzesiek S, Bax A. J. Biomol. NMR. 1993;3:627–638. doi: 10.1007/BF00198368. [DOI] [PubMed] [Google Scholar]
- (24).Clore GM, Bax A, Wingfield PT, Gronenborn AM. Biochemistry. 1990;29:5671–5676. doi: 10.1021/bi00476a004. [DOI] [PubMed] [Google Scholar]
- (25).Farrow NA, Muhandiram R, Singer AU, Pascal SM, Kay CM, Gish G, Shoelson SE, Pawson T, Forman-Kay JD, Kay LE. Biochemistry. 1994;33:5984–6003. doi: 10.1021/bi00185a040. [DOI] [PubMed] [Google Scholar]
- (26).Tjandra N, Feller SE, Pastor RW, Bax A. J Am Chem Soc. 1995;117:12562–12566. [Google Scholar]
- (27).Becker ED, Ferretti JA, Gupta RK, Weiss GH. J Magn Reson. 1980;37:381–394. [Google Scholar]
- (28).Grzesiek S, Bax A. J Am Chem Soc. 1993;115:12593–12594. [Google Scholar]
- (29).Schwieters CD, Kuszewski JJ, Clore GM. Prog Nucl Magn Reson Spect. 2006;48:47–62. [Google Scholar]
- (30).Dreyer GB, Dervan PB. Proc Natl Acad Sci U S A. 1985;82:968–972. doi: 10.1073/pnas.82.4.968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (31).Tang C, Iwahara J, Clore GM. Nature. 2006;444:383–386. doi: 10.1038/nature05201. [DOI] [PubMed] [Google Scholar]
- (32).Volkov AN, Worrall JA, Holtzmann E, Ubbink M. Proc Natl Acad Sci U S A. 2006;103:18945–18950. doi: 10.1073/pnas.0603551103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (33).Suh JY, Tang C, Clore GM. J Am Chem Soc. 2007;129:12954–12955. doi: 10.1021/ja0760978. [DOI] [PubMed] [Google Scholar]
- (34).Hernandez G, Teng CL, Bryant RG, LeMaster DM. J Am Chem Soc. 2002;124:4463–4472. doi: 10.1021/ja017340k. [DOI] [PubMed] [Google Scholar]
- (35).Kruk D, Kowalewski J. J Biol Inorg Chem. 2003;8:512–518. doi: 10.1007/s00775-003-0444-9. [DOI] [PubMed] [Google Scholar]
- (36).Miller JC, Sharp RR. J Phys Chem A. 2000;104:4889–4895. [Google Scholar]
- (37).Rubinstein M, Baram A, Luz Z. Mol Phys. 1971;20:67–80. [Google Scholar]
- (38).Gottlieb HPW, Barfield M, Doddrell DMJ. J. Chem. Phys. 1977;67:3785–3794. [Google Scholar]
- (39).Mispelter J, Momenteau M, Lhoste J-M, Berliner LJ, Reuben J, editors. Vol. 12. Plenum Press; New York: 1993. pp. 299–355. [Google Scholar]
- (40).Ma L, Jorgensen A-MM, Sorensen GO, Ulstrup J, Led JJ. J. Am. Chem. soc. 2000;122:9473–9485. [Google Scholar]
- (41).Fan H, Mark AE, Zhu J, Honig B. Proc Natl Acad Sci U S A. 2005;102:6760–6764. doi: 10.1073/pnas.0408857102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (42).Brüschweiler R, Case DA. Prog Nucl Magn Reson Spect. 1994;26:27–58. [Google Scholar]
- (43).Vögeli B, Segawa TF, Leitz D, Sobol A, Choutko A, Trzesniak D, van Gunsteren W, Riek R. J Am Chem Soc. 2009;131:17215–17225. doi: 10.1021/ja905366h. [DOI] [PubMed] [Google Scholar]
- (44).Keizers PH, Desreux JF, Overhand M, Ubbink M. J Am Chem Soc. 2007;129:9292–9293. doi: 10.1021/ja0725201. [DOI] [PubMed] [Google Scholar]
- (45).Su XC, Man B, Beeren S, Liang H, Simonsen S, Schmitz C, Huber T, Messerle BA, Otting G. J Am Chem Soc. 2008;130:10486–10487. doi: 10.1021/ja803741f. [DOI] [PubMed] [Google Scholar]
- (46).Su XC, Liang H, Loscha KV, Otting G. J Am Chem Soc. 2009;131:10352–10353. doi: 10.1021/ja9034957. [DOI] [PubMed] [Google Scholar]
- (47).Schwieters CD, Kuszewski JJ, Tjandra N, Clore GM. J Magn Reson. 2003;160:65–73. doi: 10.1016/s1090-7807(02)00014-9. [DOI] [PubMed] [Google Scholar]
- (48).Religa TL, Sprangers R, Kay LE. Science. 328:98–102. doi: 10.1126/science.1184991. [DOI] [PubMed] [Google Scholar]